Integral

ImprimirCitar

Operación en cálculo matemático

Una parte integral definida de una función puede ser representada como el área firmada de la región ligada por su gráfico. En el gráfico anterior como ejemplo, la integral de

f(x)

es el área azul (+) restringida por el área amarilla (-).

En matemáticas, una integral asigna números a funciones de una manera que describe el desplazamiento, el área, el volumen y otros conceptos que surgen al combinar datos infinitesimales. El proceso de encontrar integrales se llama integración. Junto con la diferenciación, la integración es una operación fundamental y esencial del cálculo y sirve como herramienta para resolver problemas matemáticos y físicos que involucran el área de una forma arbitraria, la longitud de una curva y el volumen de un sólido, entre otros.

Las integrales enumeradas aquí son las denominadas integrales definidas, que pueden interpretarse como el área con signo de la región en el plano que está delimitada por la gráfica de una función dada entre dos puntos en el real línea. Convencionalmente, las áreas por encima del eje horizontal del plano son positivas mientras que las áreas por debajo son negativas. Las integrales también se refieren al concepto de antiderivada, una función cuya derivada es la función dada. En este caso, se denominan integrales indefinidas. El teorema fundamental del cálculo relaciona las integrales definidas con la diferenciación y proporciona un método para calcular la integral definida de una función cuando se conoce su antiderivada.

Aunque los métodos para calcular áreas y volúmenes datan de las matemáticas griegas antiguas, los principios de integración fueron formulados de forma independiente por Isaac Newton y Gottfried Wilhelm Leibniz a fines del siglo XVII, quienes pensaron en el área bajo una curva como una suma infinita de rectángulos. de ancho infinitesimal. Bernhard Riemann más tarde dio una definición rigurosa de integrales, que se basa en un procedimiento de limitación que aproxima el área de una región curvilínea dividiendo la región en losas verticales infinitesimalmente delgadas. A principios del siglo XX, Henri Lebesgue generalizó la formulación de Riemann al introducir lo que ahora se conoce como la integral de Lebesgue; es más robusto que el de Riemann en el sentido de que una clase más amplia de funciones son integrables con Lebesgue.

Las integrales pueden generalizarse según el tipo de función y el dominio sobre el que se realiza la integración. Por ejemplo, una integral de línea se define para funciones de dos o más variables, y el intervalo de integración se reemplaza por una curva que conecta los dos extremos del intervalo. En una integral de superficie, la curva se reemplaza por una parte de una superficie en un espacio tridimensional.

Historia

Integración de precálculo

La primera técnica sistemática documentada capaz de determinar integrales es el método de agotamiento del antiguo astrónomo griego Eudoxo (ca. 370 aC), que buscaba encontrar áreas y volúmenes dividiéndolos en un número infinito de divisiones para las que se conocía el área o el volumen. Arquímedes desarrolló y empleó este método en el siglo III a. C. y lo utilizó para calcular el área de un círculo, el área de la superficie y el volumen de una esfera, el área de una elipse, el área bajo una parábola, el volumen de un segmento de un paraboloide de revolución, el volumen de un segmento de un hiperboloide de revolución y el área de una espiral.

Un método similar fue desarrollado de forma independiente en China alrededor del siglo III dC por Liu Hui, quien lo usó para encontrar el área del círculo. Este método fue utilizado más tarde en el siglo V por los matemáticos chinos padre e hijo Zu Chongzhi y Zu Geng para encontrar el volumen de una esfera.

En Oriente Medio, Hasan Ibn al-Haytham, latinizado como Alhazen (c. 965 – c. 1040 AD) derivó una fórmula para la suma de cuartas potencias. Usó los resultados para llevar a cabo lo que ahora se llamaría una integración de esta función, donde las fórmulas de las sumas de cuadrados integrales y cuartas potencias le permitieron calcular el volumen de un paraboloide.

Los siguientes avances significativos en cálculo integral no comenzaron a aparecer hasta el siglo XVII. En este momento, el trabajo de Cavalieri con su método de Indivisibles y el trabajo de Fermat comenzaron a sentar las bases del cálculo moderno, con Cavalieri calculando las integrales de $x n$ hasta el grado $n = 9$ en Cavalieri's fórmula de cuadratura. El caso n = −1 requirió la invención de una función, el logaritmo hiperbólico, logrado por cuadratura de la hipérbola en 1647.

Barrow y Torricelli dieron más pasos a principios del siglo XVII, y proporcionaron los primeros indicios de una conexión entre integración y diferenciación. Barrow proporcionó la primera prueba del teorema fundamental del cálculo. Wallis generalizó el método de Cavalieri, calculando integrales de $x$ a una potencia general, incluidas potencias negativas y potencias fraccionarias.

Leibniz y Newton

El mayor avance en la integración se produjo en el siglo XVII con el descubrimiento independiente del teorema fundamental del cálculo por parte de Leibniz y Newton. El teorema demuestra una conexión entre integración y diferenciación. Esta conexión, combinada con la relativa facilidad de diferenciación, puede aprovecharse para calcular integrales. En particular, el teorema fundamental del cálculo permite resolver una clase de problemas mucho más amplia. De igual importancia es el amplio marco matemático que desarrollaron tanto Leibniz como Newton. Dado el nombre de cálculo infinitesimal, permitió un análisis preciso de funciones dentro de dominios continuos. Este marco eventualmente se convirtió en cálculo moderno, cuya notación para integrales se extrae directamente del trabajo de Leibniz.

Formalización

Si bien Newton y Leibniz proporcionaron un enfoque sistemático para la integración, su trabajo careció de cierto grado de rigor. El obispo Berkeley atacó memorablemente los incrementos que se desvanecen utilizados por Newton, llamándolos "fantasmas de cantidades que se han ido". El cálculo adquirió una base más firme con el desarrollo de los límites. La integración fue formalizada rigurosamente por primera vez, usando límites, por Riemann. Aunque todas las funciones continuas acotadas por partes son integrables de Riemann en un intervalo acotado, posteriormente se consideraron funciones más generales, particularmente en el contexto del análisis de Fourier, a las que no se aplica la definición de Riemann, y Lebesgue formuló una definición diferente de integral., fundada en la teoría de la medida (un subcampo del análisis real). Se propusieron otras definiciones de integral, extendiendo los enfoques de Riemann y Lebesgue. Estos enfoques basados en el sistema de números reales son los más comunes hoy en día, pero existen enfoques alternativos, como una definición de integral como la parte estándar de una suma infinita de Riemann, basada en el sistema de números hiperreales.

Notación histórica

La notación para la integral indefinida fue introducida por Gottfried Wilhelm Leibniz en 1675. Adaptó el símbolo integral, ∫, de la letra ſ (s larga), de pie para summa (escrito como ſumma; latín para "sum" o "total"). La notación moderna para la integral definida, con límites por encima y por debajo del signo integral, fue utilizada por primera vez por Joseph Fourier en Mémoires de la Academia Francesa alrededor de 1819-20, reimpreso en su libro de 1822.

Isaac Newton usó una pequeña barra vertical sobre una variable para indicar la integración o colocó la variable dentro de un cuadro. La barra vertical se confundía fácilmente con $. x$ o $x''$ , que se utilizan para indicar diferenciación, y la notación de caja era difícil de reproducir para los impresores, por lo que estas notaciones no se adoptaron ampliamente.

Primer uso del término

El término fue impreso por primera vez en latín por Jacob Bernoulli en 1690: "Ergo et horum Integralia aequantur".

Terminología y notación

En general, la integral de una función de valor real $f (x)$ con respecto a una variable real $x$ en un intervalo $[a, b]$ se escribe como

{displaystyle int _{a}^{b}f(x),dx.}

El signo integral $\int$ representa integración. El símbolo $dx$ , llamado diferencial de la variable $x$ , indica que la variable de integración es $x$ . La función $f (x)$ se llama integrando, los puntos $a$ y $b$ se denominan límites (o cotas) de integración, y se dice que la integral está sobre el intervalo $[a, b]$ , llamado intervalo de integración. Se dice que una función es integrable si su integral sobre su dominio es finita. Si se especifican límites, la integral se llama integral definida.

Cuando se omiten los límites, como en

int f(x),dx,

la integral se llama integral indefinida, que representa una clase de funciones (la antiderivada) cuya derivada es el integrando. El teorema fundamental del cálculo relaciona la evaluación de integrales definidas con integrales indefinidas. Hay varias extensiones de la notación para integrales para abarcar la integración en dominios ilimitados y/o en múltiples dimensiones (ver secciones posteriores de este artículo).

En entornos avanzados, no es raro dejar fuera $dx$ cuando sólo se utiliza la simple integral Riemann, o el tipo exacto de integral es inmaterial. Por ejemplo, uno podría escribir ${textstyle int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}int _{a}^{b}f+c_{2}int _{a}^{b}g}$ para expresar la linealidad de la integral, una propiedad compartida por la integral Riemann y todas sus generalizaciones.

Interpretaciones

Aproximaciones a la

\sqrt x

de 0 a 1, con 5 particiones de extremo derecho amarillo y 12 particiones de extremo izquierdo verde

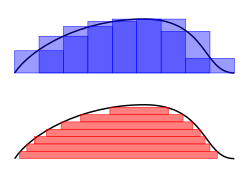
Las integrales aparecen en muchas situaciones prácticas. Por ejemplo, a partir del largo, ancho y profundidad de una piscina rectangular con fondo plano, se puede determinar el volumen de agua que puede contener, el área de su superficie y la longitud de su borde. Pero si es ovalado con el fondo redondeado, se requieren integrales para encontrar valores exactos y rigurosos para estas cantidades. En cada caso, uno puede dividir la cantidad buscada en infinitas partes infinitesimales y luego sumar las partes para lograr una aproximación precisa.

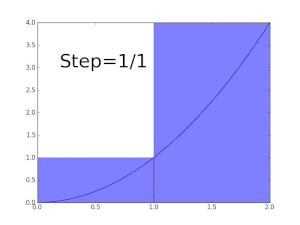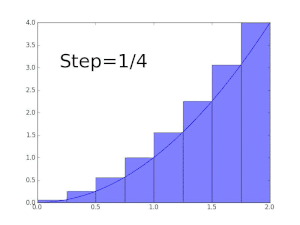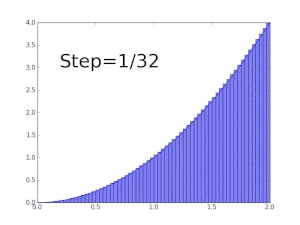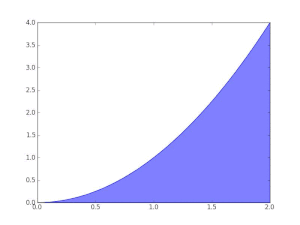
Por ejemplo, para encontrar el área de la región delimitada por la gráfica de la función $f (x) = \sqrt x$ entre x = 0 y $x = 1$ , uno puede cruzar el intervalo en cinco pasos ( $0, 1/5, 2/5,..., 1$ ), luego llene un rectángulo usando la altura del extremo derecho de cada pieza (por lo tanto, $\sqrt 0, \sqrt 1/5, \sqrt 2/5,..., \sqrt 1$ ) y suma sus áreas para obtener una aproximación de

{displaystyle textstyle {sqrt {frac {1}{5}}}left({frac {1}{5}}-0right)+{sqrt {frac {2}{5}}}left({frac {2}{5}}-{frac {1}{5}}right)+cdots +{sqrt {frac {5}{5}}}left({frac {5}{5}}-{frac {4}{5}}right)approx 0.7497,}

que es mayor que el valor exacto. Alternativamente, al reemplazar estos subintervalos por unos con la altura del extremo izquierdo de cada pieza, la aproximación que se obtiene es demasiado baja: con doce subintervalos de este tipo, el área aproximada es solo 0.6203. Sin embargo, cuando el número de piezas aumenta hasta el infinito, llegará a un límite que es el valor exacto del área buscada (en este caso, $2/3$ ). uno escribe

{displaystyle int _{0}^{1}{sqrt {x}},dx={frac {2}{3}},}

lo que significa que $2/3$ es el resultado de una suma ponderada de valores de función, $\sqrt x$ , multiplicado por los anchos de paso infinitesimales, denotados por $dx$ , en el intervalo $[0, 1]$ .

Darboux sums

Darboux sumas superiores de la función

Sí. = x 2

Darboux menor sumas de la función

Sí. = x 2

Definiciones formales

Riemann sumas convergentes

Hay muchas formas de definir formalmente una integral, no todas equivalentes. Las diferencias existen principalmente para tratar casos especiales diferentes que pueden no ser integrables bajo otras definiciones, pero también ocasionalmente por razones pedagógicas. Las definiciones más utilizadas son integrales de Riemann e integrales de Lebesgue.

Integral de Riemann

La integral de Riemann se define en términos de sumas de funciones de Riemann con respecto a las particiones etiquetadas de un intervalo. Una partición etiquetada de un intervalo cerrado $[a, b]$ en la línea real es una secuencia finita

a=x_{0}leq t_{1}leq x_{1}leq t_{2}leq x_{2}leq cdots leq x_{n-1}leq t_{n}leq x_{n}=b.,!

Esto divide el intervalo $[a, b]$ en $n$ subintervalos $[x i -1, x i]$ indexado por $i$ , cada uno de los cuales está "etiquetado" con un punto distinguido $t i \in [x i -1, x i]$ . Una suma de Riemann de una función $f$ con respecto a dicha partición etiquetada se define como

{displaystyle sum _{i=1}^{n}f(t_{i}),Delta _{i};}

por lo tanto, cada término de la suma es el área de un rectángulo con una altura igual al valor de la función en el punto distinguido del subintervalo dado, y un ancho igual al ancho del subintervalo, $Δ i = x i - x i -1$ . La malla de dicha partición etiquetada es el ancho del subintervalo más grande formado por la partición, $max i =1... n Δ i$ . La integral de Riemann de una función $f$ sobre el intervalo $[a, b]$ es igual a $S$ si:

Para todos

0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>

existe

0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ■0{displaystyle delta >0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/595d5cea06fdcaf2642caf549eda2cfc537958a9" style="vertical-align: -0.338ex; width:5.31ex; height:2.343ex;"/>

tal que, para cualquier partición etiquetada

[a,b]

con malla menos que

delta

<math alttext="{displaystyle left|S-sum _{i=1}^{n}f(t_{i}),Delta _{i}right|SilencioS− − .. i=1nf()ti)Δ Δ iSilencio.ε ε .{displaystyle left habitS-sum Delta _{i}derecha perpetuada significa 'varepsilon.}<img alt="{displaystyle left|S-sum _{i=1}^{n}f(t_{i}),Delta _{i}right|

Cuando las etiquetas elegidas dan el valor máximo (respectivamente, mínimo) de cada intervalo, la suma de Riemann se convierte en una suma de Darboux superior (respectivamente, inferior), lo que sugiere la estrecha conexión entre la integral de Riemann y la integral de Darboux.

Integral de Lebesgue

Comparison of Riemann and Lebesgue integrals

Integración de Riemann–Darboux (top) e integración de Lebesgue (abajo)

A menudo es de interés, tanto en teoría como en aplicaciones, poder pasar al límite bajo la integral. Por ejemplo, con frecuencia se puede construir una secuencia de funciones que se aproxime, en un sentido adecuado, a la solución de un problema. Entonces la integral de la función solución debe ser el límite de las integrales de las aproximaciones. Sin embargo, muchas funciones que se pueden obtener como límites no son integrables de Riemann, por lo que tales teoremas de límites no se cumplen con la integral de Riemann. Por lo tanto, es de gran importancia tener una definición de integral que permita integrar una clase más amplia de funciones.

Tal integral es la integral de Lebesgue, que aprovecha el siguiente hecho para ampliar la clase de funciones integrables: si los valores de una función se reorganizan en el dominio, la integral de una función debe permanecer igual. Así Henri Lebesgue introdujo la integral que lleva su nombre, explicando así esta integral en una carta a Paul Montel:

Tengo que pagar cierta suma, que he recogido en mi bolsillo. Saco las cuentas y monedas de mi bolsillo y las doy al acreedor en el orden que las encuentro hasta que he alcanzado la suma total. Esta es la integral Riemann. Pero puedo proceder de manera diferente. Después de haber sacado todo el dinero de mi bolsillo ordeno las cuentas y monedas según valores idénticos y luego pago los varios montones uno tras otro al acreedor. Este es mi integral.

Como dice Folland, "para calcular la integral de Riemann de $f$ , se divide el dominio $[a, b]$ en subintervalos", mientras que en la integral de Lebesgue, "uno está en efecto dividiendo el rango de $f$ ". La definición de la integral de Lebesgue comienza así con una medida, μ. En el caso más simple, la medida de Lebesgue $μ (A)$ de un intervalo $A = [a, b]$ es su ancho, $b - a$ , por lo que la integral de Lebesgue concuerda con la integral de Riemann (propia) cuando ambas existen. En casos más complicados, los conjuntos que se miden pueden estar muy fragmentados, sin continuidad y sin semejanza con los intervalos.

Usando la "partición del rango de $f$ " filosofía, la integral de una función no negativa $f : R \to R$ debe ser la suma sobre $t$ de las áreas entre una delgada franja horizontal entre $y = t$ y $y = t + dt$ . Esta área es simplemente $μ {x : f (x) > t} dt$ . Sea $f * (t) = μ {x : f (x) > t$ . La integral de Lebesgue de $f$ se define entonces por

int f=int _{0}^{infty }f^{*}(t),dt

donde la integral de la derecha es una integral de Riemann ordinaria impropia ( $f *$ es una función positiva estrictamente decreciente y, por lo tanto, tiene una integral de Riemann impropia bien definida). Para una clase adecuada de funciones (las funciones medibles) esto define la integral de Lebesgue.

Una función medible general $f$ es Lebesgue integrable si la suma de los valores absolutos de las áreas de las regiones entre las gráfico de $f$ y $x$ -axis es finito:

<math alttext="{displaystyle int _{E}|f|,dmu ∫ ∫ ESilenciofSilenciodμ μ .+JUEGO JUEGO .{displaystyle int _{E}Sobre la vida eterna,dmu}<img alt="int _{E}|f|,dmu

En ese caso, la integral es, como en el caso de Riemann, la diferencia entre el área sobre el eje $x$ y el área debajo del eje $x$ :

int _{E}f,dmu =int _{E}f^{+},dmu -int _{E}f^{-},dmu

dónde

0,\0,&{text{otherwise,}}end{cases}}\&f^{-}(x)&&{}={}max{-f(x),0}&&{}={}{begin{cases}-f(x),&{text{if }}f(x)f+()x)=max{}f()x),0}={}f()x),sif()x)■0,0,de lo contrario,f− − ()x)=max{}− − f()x),0}={}− − f()x),sif()x).0,0,De lo contrario.{fnMicrosoft Sans Serif} {f} {f} {f}} {f} {f} {f}} {f} {f}}} {f}f} {f}f}f}f}f}f}f}f}f}f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f} {f}f}f}f}f}f}f}f}f}f}\f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}\0,\0,&{text{otherwise,}}end{cases}}\&f^{-}(x)&&{}={}max{-f(x),0}&&{}={}{begin{cases}-f(x),&{text{if }}f(x)

Otras integrales

Aunque las integrales de Riemann y Lebesgue son las definiciones de integral más utilizadas, existen otras, entre ellas:

La integral Darboux, definida por las sumas Darboux (restricted Riemann sums) es igual a la integral Riemann. Una función es Darboux-integrable si y sólo si es Riemann-integrable. Darboux integrals tienen la ventaja de ser más fácil de definir que Riemann integrales.
La integral Riemann-Stieltjes, una extensión de la integral Riemann que se integra con respecto a una función en lugar de una variable.
La Lebesgue–Stieltjes integral, desarrollada por Johann Radon, que generaliza tanto las integrales Riemann–Stieltjes como Lebesgue.
La integral Daniell, que subsume la integral Lebesgue y Lebesgue–Stieltjes integral sin depender de medidas.
La integral Haar, utilizada para la integración en grupos topológicos locales compactos, introducida por Alfréd Haar en 1933.
El Henstock–Kurzweil integral, definido por Arnaud Denjoy, Oskar Perron, y (más elegantemente, como el indicador integral) Jaroslav Kurzweil, y desarrollado por Ralph Henstock.
La integral Itô y la integral Stratonovich, que definen la integración con respecto a semimartingales como el movimiento Brownian.
El Young integral, que es una especie de Riemann-Stieltjes integral con respecto a ciertas funciones de variación sin límites.
El camino áspero integral, que se define para funciones equipadas con alguna estructura adicional de "ruido duro" y generaliza la integración estocástica contra semimartingales y procesos como el movimiento fraccional de Brownian.
El Choquet integral, una integral subadditiva o superadditiva creada por el matemático francés Gustave Choquet en 1953.
El Bochner integral, una extensión de la Lebesgue integral a una clase más general de funciones, a saber, aquellas con un dominio que es un espacio de Banach.

Propiedades

Linealidad

La colección de funciones integrables de Riemann en un intervalo cerrado $[a, b]$ forma un espacio vectorial bajo las operaciones de suma puntual y multiplicación por un escalar, y la operación de integración

fmapsto int _{a}^{b}f(x);dx

es un funcional lineal en este espacio vectorial. Así, el conjunto de funciones integrables se cierra tomando combinaciones lineales, y la integral de una combinación lineal es la combinación lineal de las integrales:

int _{a}^{b}(alpha f+beta g)(x),dx=alpha int _{a}^{b}f(x),dx+beta int _{a}^{b}g(x),dx.,

Del mismo modo, el conjunto de funciones integrables de Lebesgue de valor real en un espacio de medida dado $E$ con medida $μ$ se cierra tomando combinaciones lineales y, por lo tanto, forma un espacio vectorial, y la integral de Lebesgue

fmapsto int _{E}f,dmu

es un funcional lineal en este espacio vectorial, por lo que:

int _{E}(alpha f+beta g),dmu =alpha int _{E}f,dmu +beta int _{E}g,dmu.

De manera más general, considere el espacio vectorial de todas las funciones medibles en un espacio de medida $(E, μ)$ , tomando valores en un espacio vectorial topológico completo localmente compacto $V$ sobre un campo topológico localmente compacto $K, f : E \to V$ . Entonces uno puede definir un mapa de integración abstracto asignando a cada función $f$ un elemento de $V$ o el símbolo $\infty$ ,

fmapsto int _{E}f,dmu,

que sea compatible con combinaciones lineales. En esta situación, la linealidad se cumple para el subespacio de funciones cuya integral es un elemento de $V$ (es decir, "finito&# 34;). Los casos especiales más importantes surgen cuando $K$ es $R$ , $C$ , o una extensión finita del campo $Q p$ de números p-ádicos, y $V$ es un finito -espacio vectorial dimensional sobre $K$ , y cuando $K = C$ y $V$ es un espacio de Hilbert complejo.

Linealidad, junto con algunas propiedades naturales de continuidad y normalización para una cierta clase de "simple" funciones, se pueden utilizar para dar una definición alternativa de la integral. Este es el enfoque de Daniell para el caso de funciones con valores reales en un conjunto $X$ , generalizado por Nicolas Bourbaki a funciones con valores en un espacio vectorial topológico localmente compacto. Ver Hildebrandt 1953 para una caracterización axiomática de la integral.

Desigualdades

Varias desigualdades generales son válidas para las funciones integrables de Riemann definidas en un intervalo cerrado y acotado $[a, b]$ y puede generalizarse a otras nociones de integral (Lebesgue y Daniell).

Los límites superiores e inferiores. Una función integradora $f$ on $[a, b]$ , está necesariamente ligado a ese intervalo. Así que hay números reales $m$ y $M$ así $m \leq f () x \leq M$ para todos $x$ dentro $[a, b]$ . Desde las sumas inferiores y superiores de $f$ sobre $[a, b]$ por lo tanto, están obligados por, respectivamente, $m () b - a)$ y $M () b - a)$ , sigue que ${displaystyle m(b-a)leq int _{a}^{b}f(x),dxleq M(b-a).}$
Inequities between functions. Si $f () x \leq g () x)$ para cada uno $x$ dentro $[a, b]$ entonces cada una de las sumas superiores e inferiores de $f$ está ligada arriba por las sumas superiores e inferiores, respectivamente, de $g$ . Así ${displaystyle int _{a}^{b}f(x),dxleq int _{a}^{b}g(x),dx.}$ Esta es una generalización de las desigualdades mencionadas, como $M () b - a)$ es la parte integral de la función constante con valor $M$ sobre $[a, b]$ . Además, si la desigualdad entre funciones es estricta, la desigualdad entre integrales también es estricta. Eso es, si $f () x) g () x)$ para cada uno $x$ dentro $[a, b]$ , entonces $<math alttext="{displaystyle int _{a}^{b}f(x),dx∫ ∫ abf()x)dx.∫ ∫ abg()x)dx.{displaystyle int _{a}} {b}f(x),dx obtenidosint _{a}^{b}g(x),dx.}<img alt="{displaystyle int _{a}^{b}f(x),dx$
Subintervalos. Si $[c, d]$ es un subintervalo de $[a, b]$ y $f () x)$ no negativo para todos $x$ , entonces ${displaystyle int _{c}^{d}f(x),dxleq int _{a}^{b}f(x),dx.}$
Productos y valores absolutos de funciones. Si $f$ y $g$ son dos funciones, entonces podemos considerar sus productos y poderes punteros, y valores absolutos: ${displaystyle (fg)(x)=f(x)g(x),;f^{2}(x)=(f(x))^{2},;|f|(x)=|f(x)|.}$ Si $f$ Riemann-integrable en $[a, b]$ entonces lo mismo es verdad $Silencio f Silencio$ , y ${displaystyle left|int _{a}^{b}f(x),dxright|leq int _{a}^{b}|f(x)|,dx.}$ Además, si $f$ y $g$ ambos Riemann-integrable entonces $fg$ también Riemann-integrable, y ${displaystyle left(int _{a}^{b}(fg)(x),dxright)^{2}leq left(int _{a}^{b}f(x)^{2},dxright)left(int _{a}^{b}g(x)^{2},dxright).}$ Esta desigualdad, conocida como la desigualdad Cauchy-Schwarz, desempeña un papel prominente en la teoría espacial de Hilbert, donde el lado izquierdo se interpreta como el producto interior de dos funciones cuadradas-integrables $f$ y $g$ en el intervalo $[a, b]$ .
La desigualdad de Hölder. Supongamos que $p$ y $q$ son dos números reales, $1 \leq p, q \leq$ con $1 / p + 1 / q = 1$ , y $f$ y $g$ son dos funciones integradas Riemann. Entonces las funciones $Silencio f Silencio p$ y $Silencio g Silencio q$ son también integrados y la siguiente desigualdad de Hölder sostiene: ${displaystyle left|int f(x)g(x),dxright|leq left(int left|f(x)right|^{p},dxright)^{1/p}left(int left|g(x)right|^{q},dxright)^{1/q}.}$ Para $p = q = 2$ La desigualdad de Hölder se convierte en la desigualdad Cauchy-Schwarz.
Inequidad de Minkowski. Supongamos que $p \geq 1$ es un número real y $f$ y $g$ son funciones Riemann-integrable. Entonces... $Silencio f Silencio p, Silencio g Silencio p$ y $Silencio f + g Silencio p$ son también Riemann-integrable y la siguiente desigualdad Minkowski sostiene: ${displaystyle left(int left|f(x)+g(x)right|^{p},dxright)^{1/p}leq left(int left|f(x)right|^{p},dxright)^{1/p}+left(int left|g(x)right|^{p},dxright)^{1/p}.}$ Un análogo de esta desigualdad para Lebesgue integral se utiliza en la construcción de espacios Lp.

Convenios

En esta sección, $f$ es una función integrable de Riemann de valor real. la integral

int _{a}^{b}f(x),dx

en un intervalo $[a, b]$ se define si $a < b$ . Esto significa que las sumas superior e inferior de la función $f$ se evalúan en una partición $a = x 0 \leq x 1 \leq... \leq x n = b$ cuyos valores $x i$ están aumentando. Geométricamente, esto significa que la integración tiene lugar "de izquierda a derecha", evaluando $f$ dentro de intervalos [x_i , x_i +1] donde un intervalo con un índice más alto se encuentra a la derecha de uno con un índice más bajo. Los valores $a$ y $b$ , los puntos finales del intervalo, se denominan límites de integración de $f$ . Las integrales también se pueden definir si $a > b$ :

int _{a}^{b}f(x),dx=-int _{b}^{a}f(x),dx.

Con $a = b$ , esto implica:

int _{a}^{a}f(x),dx=0.

La primera convención es necesaria al tomar integrales sobre subintervalos de $[a, b]$ ; el segundo dice que una integral tomada sobre un intervalo degenerado, o un punto, debe ser cero. Una razón para la primera convención es que la integrabilidad de $f$ en un intervalo $[a, b]$ implica que $f$ es integrable en cualquier subintervalo $[c, d]$ , pero en particular las integrales tienen la propiedad de que si $c$ es cualquier elemento de $[a, b]$ , entonces:

int _{a}^{b}f(x),dx=int _{a}^{c}f(x),dx+int _{c}^{b}f(x),dx.

Con la primera convención, la relación resultante

{begin{aligned}int _{a}^{c}f(x),dx&{}=int _{a}^{b}f(x),dx-int _{c}^{b}f(x),dx\&{}=int _{a}^{b}f(x),dx+int _{b}^{c}f(x),dxend{aligned}}

está entonces bien definido para cualquier permutación cíclica de $a$ , $b$ y $c$ .

Teorema fundamental del cálculo

El teorema fundamental del cálculo es la afirmación de que la diferenciación y la integración son operaciones inversas: si una función continua se integra primero y luego se deriva, se recupera la función original. Una consecuencia importante, a veces llamada el segundo teorema fundamental del cálculo, permite calcular integrales mediante el uso de una antiderivada de la función que se va a integrar.

Primer teorema

Sea $f$ una función continua de valor real definida en un intervalo cerrado $[a, b]$ . Sea $F$ la función definida, para todos $x$ en $[a, b]$ , por

F(x)=int _{a}^{x}f(t),dt.

Entonces, $F$ es continua en $[a, b]$ , diferenciable en el intervalo abierto $(a, b)$ , y

F'(x)=f(x)

para todos los $x$ en $(a, b)$ .

Segundo teorema

Sea $f$ una función de valor real definida en un intervalo cerrado [ $a, b$ ] que admite una antiderivada $F$ sobre [a, b]. Es decir, $f$ y $F$ son funciones tales que para todas las $x$ en $[a, b]$ ,

f(x)=F'(x).

Si $f$ es integrable en $[a, b]$ entonces

int _{a}^{b}f(x),dx=F(b)-F(a).

Extensiones

Integrales impropias

La integral inadecuada

int _{0}^{infty }{frac {dx}{(x+1){sqrt {x}}}}=pi

tiene intervalos sin límites para el dominio y el rango.

Un "adecuado" La integral de Riemann asume que el integrando está definido y es finito en un intervalo cerrado y acotado, delimitado por los límites de integración. Una integral impropia ocurre cuando una o más de estas condiciones no se cumplen. En algunos casos, tales integrales pueden definirse considerando el límite de una secuencia de integrales de Riemann propias en intervalos progresivamente mayores.

Si el intervalo no está acotado, por ejemplo en su extremo superior, entonces la integral impropia es el límite cuando ese extremo tiende a infinito:

{displaystyle int _{a}^{infty }f(x),dx=lim _{bto infty }int _{a}^{b}f(x),dx.}

Si el integrando solo está definido o es finito en un intervalo semiabierto, por ejemplo $(a, b]$ , entonces nuevamente un límite puede proporcionar un resultado finito:

{displaystyle int _{a}^{b}f(x),dx=lim _{varepsilon to 0}int _{a+epsilon }^{b}f(x),dx.}

Es decir, la integral impropia es el límite de las integrales propias cuando un extremo del intervalo de integración se aproxima a un número real específico, o $\infty$ , o $-\infty$ . En casos más complicados, se requieren límites en ambos extremos o en puntos interiores.

Integración múltiple

Doble volumen de computaciones integrales bajo una superficie

z=f(x,y)

Así como la parte integral definida de una función positiva de una variable representa el área de la región entre el gráfico de la función y la x-Eje, el doble integral de una función positiva de dos variables representa el volumen de la región entre la superficie definida por la función y el plano que contiene su dominio. Por ejemplo, una función en dos dimensiones depende de dos variables reales, x y Sí., y el integral de una función f sobre el rectángulo R dado como el producto cartesiano de dos intervalos $R=[a,b]times [c,d]$ puede ser escrito

int _{R}f(x,y),dA

donde el diferencial $dA$ indica que la integración se toma con respecto al área. Esta integral doble se puede definir mediante sumas de Riemann y representa el volumen (con signo) bajo el gráfico de $z = f (x, y)$ sobre el dominio R. En condiciones adecuadas (por ejemplo, si f es continua), el teorema de Fubini establece que esta integral se puede expresar como una integral iterada equivalente

int _{a}^{b}left[int _{c}^{d}f(x,y),dyright],dx.

Esto reduce el problema de calcular una integral doble a calcular integrales unidimensionales. Debido a esto, otra notación para la integral sobre R usa un signo de integral doble:

{displaystyle iint _{R}f(x,y),dA.}

Es posible integrar más dominios generales. La parte integral de una función f, con respecto al volumen, sobre un No...Región dimensional D de $mathbb {R} ^{n}$ es denotado por símbolos tales como:

{displaystyle int _{D}f(mathbf {x})d^{n}mathbf {x} =int _{D}f,dV.}

Integrales de línea e integrales de superficie

Una línea integral suma elementos a lo largo de una curva.

El concepto de integral se puede extender a dominios más generales de integración, como líneas curvas y superficies dentro de espacios de mayor dimensión. Estas integrales se conocen como integrales de línea e integrales de superficie, respectivamente. Estos tienen importantes aplicaciones en física, como cuando se trata de campos vectoriales.

Una integral de línea (a veces llamada integral de trayectoria) es una integral en la que la función que se va a integrar se evalúa a lo largo de una curva. Se utilizan varias integrales de línea diferentes. En el caso de una curva cerrada también se le llama integral de contorno.

La función a integrar puede ser un campo escalar o un campo vectorial. El valor de la integral de línea es la suma de los valores del campo en todos los puntos de la curva, ponderada por alguna función escalar en la curva (comúnmente longitud de arco o, para un campo vectorial, el producto escalar del campo vectorial con un diferencial vector en la curva). Esta ponderación distingue la integral de línea de integrales más simples definidas en intervalos. Muchas fórmulas simples en física tienen análogos continuos naturales en términos de integrales de línea; por ejemplo, el hecho de que el trabajo es igual a la fuerza, $F$ , multiplicado por el desplazamiento, $s$ , puede expresarse (en términos de cantidades vectoriales) como:

W=mathbf {F} cdot mathbf {s}.

Para un objeto que se mueve a lo largo de una ruta $C$ en un campo vectorial $F$ como un campo eléctrico o un campo gravitatorio, el trabajo total realizado por el campo sobre el objeto se obtiene sumando el trabajo diferencial realizado al moverse desde $s$ a $s + d s$ . Esto da la integral de línea

W=int _{C}mathbf {F} cdot dmathbf {s}.

La definición de la superficie integral se basa en dividir la superficie en pequeños elementos de superficie.

Una integral de superficie generaliza las integrales dobles a la integración sobre una superficie (que puede ser un conjunto curvo en el espacio); se puede considerar como la integral doble análoga a la integral de línea. La función a integrar puede ser un campo escalar o un campo vectorial. El valor de la integral de superficie es la suma del campo en todos los puntos de la superficie. Esto se puede lograr dividiendo la superficie en elementos de superficie, que proporcionan la partición para las sumas de Riemann.

Para ver un ejemplo de aplicaciones de integrales de superficie, considere un campo vectorial $v$ en una superficie $S$ ; es decir, para cada punto $x$ en $S$ , $v (x)$ es un vector. Imagine que un fluido fluye a través de $S$ , tal que $v (x)$ determina la velocidad del fluido en $x$ . El flujo se define como la cantidad de fluido que fluye a través de $S$ en la unidad de tiempo. Para encontrar el flujo, se necesita tomar el producto escalar de $v$ con la superficie unitaria normal a $S$ en cada punto, lo que dará un campo escalar, que se integra sobre la superficie:

{displaystyle int _{S}{mathbf {v} }cdot ,d{mathbf {S} }.}

El flujo de fluido en este ejemplo puede provenir de un fluido físico como el agua o el aire, o de un flujo eléctrico o magnético. Así, las integrales de superficie tienen aplicaciones en física, particularmente con la teoría clásica del electromagnetismo.

Integrales de contorno

En análisis complejos, el integrado es una función de valor complejo de una variable compleja $z$ en lugar de una función real de una variable real $x$ . Cuando una función compleja se integra a lo largo de una curva $gamma$ en el plano complejo, la integral se denota de la siguiente manera

{displaystyle int _{gamma }f(z),dz.}

Esto se conoce como integral de contorno.

Integrales de formas diferenciales

Una forma diferencial es un concepto matemático en los campos del cálculo multivariable, la topología diferencial y los tensores. Las formas diferenciales están organizadas por grado. Por ejemplo, una forma única es una suma ponderada de los diferenciales de las coordenadas, como:

E(x,y,z),dx+F(x,y,z),dy+G(x,y,z),dz

donde E, F, G son funciones en tres dimensiones. Una forma única diferencial se puede integrar sobre un camino orientado, y la integral resultante es solo otra forma de escribir una integral de línea. Aquí los diferenciales básicos dx, dy, dz miden longitudes orientadas infinitesimales paralelas a los tres ejes de coordenadas.

Una forma diferencial de dos es una suma de la forma

{displaystyle G(x,y,z),dxwedge dy+E(x,y,z),dywedge dz+F(x,y,z),dzwedge dx.}

Aquí las dos formas básicas $dxwedge dy,dzwedge dx,dywedge dz$ mide áreas orientadas paralelas a las coordenadas de dos planos. El símbolo $wedge$ denota el producto de cuña, que es similar al producto cruzado en el sentido de que el producto de cuña de dos formas que representan longitudes orientadas representa un área orientada. Una dos formas se puede integrar sobre una superficie orientada, y la integral resultante es equivalente a la superficie integral dando el flujo de $Emathbf {i} +Fmathbf {j} +Gmathbf {k}$ .

A diferencia del producto vectorial y el cálculo vectorial tridimensional, el producto cuña y el cálculo de formas diferenciales tienen sentido en dimensiones arbitrarias y en variedades más generales (curvas, superficies y sus análogos de dimensiones superiores). La derivada exterior juega el papel del gradiente y el rotacional del cálculo vectorial, y Stokes' generaliza simultáneamente los tres teoremas del cálculo vectorial: el teorema de la divergencia, el teorema de Green y el teorema de Kelvin-Stokes.

Resúmenes

El equivalente discreto de la integración es la suma. Las sumas y las integrales se pueden poner sobre los mismos fundamentos utilizando la teoría de las integrales de Lebesgue o el cálculo de escala de tiempo.

Integrales funcionales

Una integración que no se realiza sobre una variable (o, en física, sobre una dimensión espacial o temporal), sino sobre un espacio de funciones, se denomina integral funcional.

Aplicaciones

Las integrales se utilizan ampliamente en muchas áreas. Por ejemplo, en la teoría de la probabilidad, las integrales se utilizan para determinar la probabilidad de que alguna variable aleatoria se encuentre dentro de un cierto rango. Además, la integral bajo una función de densidad de probabilidad completa debe ser igual a 1, lo que proporciona una prueba de si una función sin valores negativos podría ser una función de densidad o no.

Los integrales se pueden utilizar para calcular el área de una región bidimensional que tiene un límite curvado, así como para calcular el volumen de un objeto tridimensional que tiene un límite curvado. El área de una región bidimensional se puede calcular utilizando la integral definida antes mencionada. El volumen de un objeto tridimensional como un disco o una lavadora se puede computar mediante la integración del disco utilizando la ecuación para el volumen de un cilindro, ${displaystyle pi r^{2}h}$ , donde $r$ es el radio. En el caso de un disco simple creado girando una curva sobre el $x$ -eje, el radio es dado por $f () x)$ , y su altura es el diferencial $dx$ . Usando una integral con límites $a$ y $b$ , el volumen del disco es igual a:

{displaystyle pi int _{a}^{b}f^{2}(x),dx.}

[a,b]

{displaystyle x(b)-x(a)=int _{a}^{b}v(t),dt,}

Donde $v(t)$ es la velocidad expresada como una función del tiempo. El trabajo realizado por una fuerza $F(x)$ (según función de posición) de una posición inicial $A$ a una posición final $B$ es:

{displaystyle W_{Arightarrow B}=int _{A}^{B}F(x),dx.}

Las integrales también se usan en termodinámica, donde la integración termodinámica se usa para calcular la diferencia de energía libre entre dos estados dados.

Cálculo

Analítica

(feminine)

La técnica más básica para calcular integrales definidas de una variable real se basa en el teorema fundamental del cálculo. Sea $f (x)$ la función de $x$ para ser integrado en un intervalo dado $[a, b]$ . Luego, encuentra una antiderivada de $f$ ; es decir, una función $F$ tal que $F' = f$ en el intervalo. Siempre que el integrando y la integral no tengan singularidades en el camino de la integración, por el teorema fundamental del cálculo,

{displaystyle int _{a}^{b}f(x),dx=F(b)-F(a).}

A veces es necesario utilizar una de las muchas técnicas que se han desarrollado para evaluar integrales. La mayoría de estas técnicas reescriben una integral como una diferente que, con suerte, es más manejable. Las técnicas incluyen integración por sustitución, integración por partes, integración por sustitución trigonométrica e integración por fracciones parciales.

Existen métodos alternativos para calcular integrales más complejas. Muchas integrales no elementales pueden expandirse en una serie de Taylor e integrarse término por término. Ocasionalmente, la serie infinita resultante se puede sumar analíticamente. También se puede usar el método de convolución usando las funciones G de Meijer, asumiendo que el integrando se puede escribir como un producto de las funciones G de Meijer. También hay muchas formas menos comunes de calcular integrales definidas; por ejemplo, la identidad de Parseval se puede usar para transformar una integral sobre una región rectangular en una suma infinita. Ocasionalmente, una integral puede evaluarse mediante un truco; para ver un ejemplo de esto, consulte Integral de Gauss.

Los cálculos de volúmenes de sólidos de revolución generalmente se pueden realizar con integración de disco o integración de capa.

Los resultados específicos que se han obtenido mediante varias técnicas se recopilan en la lista de integrales.

Simbólico

Muchos problemas de matemáticas, física e ingeniería involucran integración donde se desea una fórmula explícita para la integral. Se han compilado y publicado extensas tablas de integrales a lo largo de los años para este propósito. Con la difusión de las computadoras, muchos profesionales, educadores y estudiantes han recurrido a los sistemas de álgebra computacional que están específicamente diseñados para realizar tareas difíciles o tediosas, incluida la integración. La integración simbólica ha sido una de las motivaciones para el desarrollo de los primeros sistemas de este tipo, como Macsyma y Maple.

Una dificultad matemática importante en la integración simbólica es que, en muchos casos, una función relativamente simple no tiene integrales que puedan expresarse en forma cerrada que involucra solo funciones elementales, incluidas funciones racionales y exponenciales, logaritmo, funciones trigonométricas y funciones trigonométricas inversas. y las operaciones de multiplicación y composición. El algoritmo de Risch proporciona un criterio general para determinar si la antiderivada de una función elemental es elemental y calcularla si lo es. Sin embargo, las funciones con expresiones cerradas de antiderivadas son la excepción y, en consecuencia, los sistemas de álgebra computarizados no tienen ninguna esperanza de poder encontrar una antiderivada para una función elemental construida aleatoriamente. En el lado positivo, si los 'bloques de construcción' dado que las antiderivadas se fijan de antemano, aún puede ser posible decidir si la antiderivada de una función dada se puede expresar usando estos bloques y operaciones de multiplicación y composición, y encontrar la respuesta simbólica siempre que exista. El algoritmo de Risch, implementado en Mathematica, Maple y otros sistemas de álgebra computacional, hace precisamente eso para funciones y antiderivadas construidas a partir de funciones racionales, radicales, logaritmos y funciones exponenciales.

Algunos integrandos especiales ocurren con la suficiente frecuencia como para merecer un estudio especial. En particular, puede ser útil tener, en el conjunto de antiderivadas, las funciones especiales (como las funciones de Legendre, la función hipergeométrica, la función gamma, la función gamma incompleta, etc.). Extender el algoritmo de Risch para incluir tales funciones es posible pero desafiante y ha sido un tema de investigación activo.

Más recientemente ha surgido un nuevo enfoque que utiliza funciones D-finitas, que son las soluciones de ecuaciones diferenciales lineales con coeficientes polinómicos. La mayoría de las funciones elementales y especiales son D-finitas, y la integral de una función D-finita también es una función D-finita. Esto proporciona un algoritmo para expresar la antiderivada de una función D-finita como la solución de una ecuación diferencial. Esta teoría también permite calcular la integral definida de una función D como la suma de una serie dada por los primeros coeficientes y proporciona un algoritmo para calcular cualquier coeficiente.

Numérico

Numerical quadrature methods: rectangle method, trapezoidal rule, Romberg's method, Gaussian quadrature

Las integrales definidas se pueden aproximar usando varios métodos de integración numérica. El método del rectángulo se basa en dividir la región debajo de la función en una serie de rectángulos correspondientes a los valores de la función y multiplicar por el ancho del paso para encontrar la suma. Un mejor enfoque, la regla trapezoidal, reemplaza los rectángulos usados en una suma de Riemann con trapezoides. La regla trapezoidal pondera el primer y el último valor a la mitad, luego se multiplica por el ancho del paso para obtener una mejor aproximación. La idea detrás de la regla trapezoidal, que las aproximaciones más precisas a la función producen mejores aproximaciones a la integral, se puede llevar más allá: la regla de Simpson aproxima el integrando mediante una función cuadrática por partes.

Las sumas de Riemann, la regla trapezoidal y la regla de Simpson son ejemplos de una familia de reglas de cuadratura llamadas fórmulas de Newton-Cotes. La regla de cuadratura de Newton-Cotes de grado $n$ aproxima el polinomio en cada subintervalo en un grado $n$ polinomio. Este polinomio se elige para interpolar los valores de la función en el intervalo. Las aproximaciones de Newton-Cotes de mayor grado pueden ser más precisas, pero requieren más evaluaciones de funciones y pueden sufrir imprecisiones numéricas debido al fenómeno de Runge. Una solución a este problema es la cuadratura de Clenshaw-Curtis, en la que el integrando se aproxima expandiéndolo en términos de polinomios de Chebyshev.

El método de Romberg reduce a la mitad los anchos de paso de forma incremental, dando aproximaciones trapezoidales indicadas por $T (h 0)$ , $T (h 1)$ , etc. encendido, donde $h k +1$ es la mitad de <span class="texhtml" h_k. Para cada nuevo tamaño de paso, solo es necesario calcular la mitad de los nuevos valores de la función; los demás se transfieren del tamaño anterior. Luego interpola un polinomio a través de las aproximaciones y extrapola a $T (0)$ . La cuadratura gaussiana evalúa la función en las raíces de un conjunto de polinomios ortogonales. Un método gaussiano de $n$ puntos es exacto para polinomios de grado hasta $2 n - 1$ .

El cálculo de integrales de dimensiones superiores (por ejemplo, cálculos de volumen) hace un uso importante de alternativas como la integración de Monte Carlo.

Mecánica

El área de una forma bidimensional arbitraria se puede determinar usando un instrumento de medición llamado planímetro. El volumen de objetos irregulares se puede medir con precisión por el fluido desplazado cuando el objeto se sumerge.

Geométrica

El área a veces se puede encontrar a través de construcciones geométricas con compás y regla de un cuadrado equivalente.

Integración por diferenciación

Kempf, Jackson y Morales demostraron relaciones matemáticas que permiten que una integral sea calculada por medio de diferenciación. Su cálculo implica la función Dirac delta y el operador derivado parcial $partial _{x}$ . Esto también se puede aplicar a las integrales funcionales, permitiéndoles ser computados por la diferenciación funcional.

Ejemplos

Uso del teorema fundamental del cálculo

El teorema fundamental del cálculo permite cálculos sencillos de funciones básicas.

${displaystyle int _{0}^{pi }sin(x)dx=-cos(x){big |}_{x=0}^{x=pi }=-cos(pi)-(-cos(0))=2}$

Contenido relacionado

Más resultados...