Integración por partes

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método matemático en cálculo

En cálculo, y más generalmente en análisis matemático, la integración por partes o integración parcial es un proceso que encuentra la integral de un producto de funciones en términos de la integral del producto de su derivada y antiderivada. Se usa con frecuencia para transformar la antiderivada de un producto de funciones en una antiderivada para la cual se puede encontrar una solución más fácilmente. La regla se puede considerar como una versión integral de la regla del producto de diferenciación.

La fórmula de integración por partes establece:

{displaystyle {begin{aligned}int _{a}^{b}u(x)v'(x),dx&={Big [}u(x)v(x){Big ]}_{a}^{b}-int _{a}^{b}u'(x)v(x),dx\&=u(b)v(b)-u(a)v(a)-int _{a}^{b}u'(x)v(x),dx.end{aligned}}}

O, dejar ${displaystyle u=u(x)}$ y ${displaystyle du=u'(x),dx}$ mientras ${displaystyle v=v(x)}$ y ${displaystyle dv=v'(x),dx}$ , la fórmula se puede escribir más compactamente:

{displaystyle int u,dv = uv-int v,du.}

El matemático Brook Taylor descubrió la integración por partes y publicó la idea por primera vez en 1715. Existen formulaciones más generales de integración por partes para las integrales de Riemann-Stieltjes y Lebesgue-Stieltjes. El análogo discreto de las sucesiones se llama suma por partes.

Teorema

Producto de dos funciones

El teorema se puede derivar de la siguiente manera. Para dos funciones continuamente diferenciables u(x) y v(x), la regla del producto establece:

{displaystyle {Big (}u(x)v(x){Big)}'=v(x)u'(x)+u(x)v'(x).}

Integrando ambos lados con respecto a x,

{displaystyle int {Big (}u(x)v(x){Big)}',dx=int u'(x)v(x),dx+int u(x)v'(x),dx,}

y notando que una integral indefinida es una antiderivada da

{displaystyle u(x)v(x)=int u'(x)v(x),dx+int u(x)v'(x),dx,}

donde descuidamos escribir la constante de integración. Esto produce la fórmula para integración por partes:

{displaystyle int u(x)v'(x),dx=u(x)v(x)-int u'(x)v(x),dx,}

o en términos de las diferencias ${displaystyle du=u'(x),dx}$ , ${displaystyle dv=v'(x),dx,quad }$

{displaystyle int u(x),dv=u(x)v(x)-int v(x),du.}

Esto debe entenderse como una igualdad de funciones con una constante no especificada agregada a cada lado. Tomando la diferencia de cada lado entre dos valores x = a y x = b y aplicando el teorema fundamental de el cálculo da la versión integral definida:

{displaystyle int _{a}^{b}u(x)v'(x),dx=u(b)v(b)-u(a)v(a)-int _{a}^{b}u'(x)v(x),dx.}

uvdxvvvvudx

Validez para funciones menos fluidas

No es necesario que u y v sean continuamente diferenciables. La integración por partes funciona si u es absolutamente continua y la función designada v′ es Lebesgue integrable (pero no necesariamente continua). (Si v′ tiene un punto de discontinuidad entonces su antiderivada v puede no tener una derivada en ese punto).

Si el intervalo de integración no es compacto, entonces no es necesario que u sea absolutamente continuo en todo el intervalo o que v′ sea Lebesgue integrable en el intervalo, como se verá en un par de ejemplos (en los que u y v son continuos y continuamente diferenciables). Por ejemplo, si

{displaystyle u(x)=e^{x}/x^{2},,v'(x)=e^{-x}}

u no es absolutamente continua en el intervalo $[1, \infty)$ , pero sin embargo

{displaystyle int _{1}^{infty }u(x)v'(x),dx={Big [}u(x)v(x){Big ]}_{1}^{infty }-int _{1}^{infty }u'(x)v(x),dx}

tan largo como ${displaystyle left[u(x)v(x)right]_{1}^{infty }}$ se toma para significar el límite ${displaystyle u(L)v(L)-u(1)v(1)}$ como ${displaystyle Lto infty }$ y mientras los dos términos en el lado derecho sean finitos. Esto es sólo cierto si elegimos ${displaystyle v(x)=-e^{-x}.}$ Del mismo modo, si

{displaystyle u(x)=e^{-x},,v'(x)=x^{-1}sin(x)}

v′ no es Lebesgue integrable en el intervalo $[1, \infty)$ , pero no obstante

{displaystyle int _{1}^{infty }u(x)v'(x),dx={Big [}u(x)v(x){Big ]}_{1}^{infty }-int _{1}^{infty }u'(x)v(x),dx}

También se pueden encontrar fácilmente ejemplos similares en los que u y v no son continuamente diferenciables.

Además, si $f(x)$ es una función de variación atada en el segmento $[a,b],$ y $varphi (x)$ es diferente en $[a,b],$ entonces

{displaystyle int _{a}^{b}f(x)varphi '(x),dx=-int _{-infty }^{infty }{widetilde {varphi }}(x),d({widetilde {chi }}_{[a,b]}(x){widetilde {f}}(x)),}

Donde ${displaystyle d(chi _{[a,b]}(x){widetilde {f}}(x))}$ denota la medida firmada correspondiente a la función de variación atada ${displaystyle chi _{[a,b]}(x)f(x)}$ , y funciones ${displaystyle {widetilde {f}},{widetilde {varphi }}}$ are extensions of ${displaystyle f,varphi }$ a ${displaystyle mathbb {R}}$ que son respectivamente de variación atada y diferenciable.

Producto de muchas funciones

Integrando la regla del producto para tres funciones multiplicadas, u(x), v(x), w(x), da un resultado similar:

{displaystyle int _{a}^{b}uv,dw = {Big [}uvw{Big ]}_{a}^{b}-int _{a}^{b}uw,dv-int _{a}^{b}vw,du.}

En general, para n factores

{displaystyle left(prod _{i=1}^{n}u_{i}(x)right)' = sum _{j=1}^{n}u_{j}'(x)prod _{ineq j}^{n}u_{i}(x),}

lo que conduce a

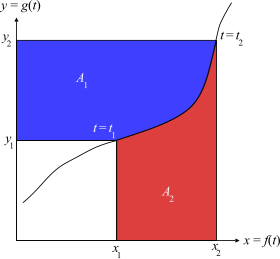
{displaystyle left[prod _{i=1}^{n}u_{i}(x)right]_{a}^{b} = sum _{j=1}^{n}int _{a}^{b}u_{j}'(x)prod _{ineq j}^{n}u_{i}(x).}

Visualización

Interpretación gráfica del teorema. La curva es parametrizada por la variable t.

Considere una curva paramétrica por (x, y) = (f(t), g(t)). Suponiendo que la curva es localmente uno a uno e integrable, podemos definir

x(y)=f(g^{-1}(y))

y(x)=g(f^{-1}(x))

El área de la región azul es

{displaystyle A_{1}=int _{y_{1}}^{y_{2}}x(y),dy}

Del mismo modo, el área de la región roja es

{displaystyle A_{2}=int _{x_{1}}^{x_{2}}y(x),dx}

El área total A₁ + A₂ es igual al área del rectángulo mayor, x₂y₂, menos el área del más pequeño, x₁y₁:

{displaystyle overbrace {int _{y_{1}}^{y_{2}}x(y),dy} ^{A_{1}}+overbrace {int _{x_{1}}^{x_{2}}y(x),dx} ^{A_{2}} = {biggl.}xcdot y(x){biggl |}_{x_{1}}^{x_{2}} = {biggl.}ycdot x(y){biggl |}_{y_{1}}^{y_{2}}}

O, en términos de t,

{displaystyle int _{t_{1}}^{t_{2}}x(t),dy(t)+int _{t_{1}}^{t_{2}}y(t),dx(t) = {biggl.}x(t)y(t){biggl |}_{t_{1}}^{t_{2}}}

O, en términos de integrales indefinidas, esto se puede escribir como

{displaystyle int x,dy+int y,dx = xy}

Reorganización:

{displaystyle int x,dy = xy-int y,dx}

Por lo tanto, se puede pensar que la integración por partes deriva el área de la región azul del área de los rectángulos y la de la región roja.

Esta visualización también explica por qué la integración por partes puede ayudar a encontrar la parte integral de una función inversa f⁻¹()x) cuando la parte integral de la función f()x) es conocido. De hecho, las funciones x()Sí.) y Sí.()x) son inversos, y el integral ∫ xdy puede ser calculado como arriba de conocer la integral ∫ Sí.dx. En particular, esto explica el uso de la integración por partes para integrar las funciones logaritmo y trigonométrica inversa. De hecho, si $f$ es una función diferenciable uno a uno en un intervalo, luego la integración por partes se puede utilizar para derivar una fórmula para la parte integral de $f^{-1}$ en términos de la integral $f$ . Esto se demuestra en el artículo, Integral de funciones inversas.

Aplicaciones

Encontrar antiderivadas

La integración por partes es un proceso heurístico más que puramente mecánico para resolver integrales; dada una sola función para integrar, la estrategia típica es separar cuidadosamente esta función única en un producto de dos funciones u(x)v(x) tal que la integral residual de la fórmula de integración por partes es más fácil de evaluar que la función simple. El siguiente formulario es útil para ilustrar la mejor estrategia a seguir:

{displaystyle int uv dx=uint v dx-int left(u'int v dxright) dx.}

En el lado derecho, se diferencia u y se integra v; en consecuencia, es útil elegir u como una función que simplifica cuando se diferencia, o elegir v como una función que se simplifica cuando se integra. Como un ejemplo simple, considere:

{displaystyle int {frac {ln(x)}{x^{2}}} dx.}

Dado que la derivada de ln(x) es 1/x, uno hace (ln(x)) parte u; ya que la antiderivada de 1/x² es −1/x, uno hace 1/x² dx parte dv. La fórmula ahora produce:

{displaystyle int {frac {ln(x)}{x^{2}}} dx=-{frac {ln(x)}{x}}-int {biggl (}{frac {1}{x}}{biggr)}{biggl (}-{frac {1}{x}}{biggr)} dx.}

La antiderivada de −1/x² se puede encontrar con la regla de la potencia y es 1/x.

Alternativamente, uno puede elegir u y v tales que el producto u′ (∫v dx) se simplifica debido a la cancelación. Por ejemplo, supongamos que se desea integrar:

{displaystyle int sec ^{2}(x)cdot ln {Big (}{bigl |}sin(x){bigr |}{Big)} dx.}

Si elegimos u(x) = ln(|sin(x)|) y v (x) = sec²x, entonces u deriva a 1/ tan x usando la regla de la cadena y v se integra a tan x; por lo que la fórmula da:

{displaystyle int sec ^{2}(x)cdot ln {Big (}{bigl |}sin(x){bigr |}{Big)} dx=tan(x)cdot ln {Big (}{bigl |}sin(x){bigr |}{Big)}-int tan(x)cdot {frac {1}{tan(x)}},dx.}

El integrando se simplifica a 1, por lo que la antiderivada es x. Encontrar una combinación simplificadora frecuentemente involucra experimentación.

En algunas aplicaciones, puede que no sea necesario asegurarse de que la integral producida por la integración por partes tenga una forma simple; por ejemplo, en el análisis numérico, puede ser suficiente que tenga una magnitud pequeña y, por lo tanto, contribuya solo con un término de error pequeño. Algunas otras técnicas especiales se muestran en los ejemplos a continuación.

Polinomios y funciones trigonométricas

Para calcular

{displaystyle I=int xcos(x) dx}

let:

{displaystyle u=x Rightarrow du=dx}

{displaystyle dv=cos(x) dx Rightarrow v=int cos(x) dx=sin(x)}

entonces:

{displaystyle {begin{aligned}int xcos(x) dx&=int u dv\&=ucdot v-int v,du\&=xsin(x)-int sin(x) dx\&=xsin(x)+cos(x)+C,end{aligned}}}

donde C es una constante de integración.

Para potencias mayores de x en la forma

{displaystyle int x^{n}e^{x} dx, int x^{n}sin(x) dx, int x^{n}cos(x) dx}

Usar repetidamente la integración por partes puede evaluar integrales como estas; cada aplicación del teorema reduce la potencia de x en uno.

Funciones exponenciales y trigonométricas

Un ejemplo comúnmente utilizado para examinar el funcionamiento de la integración por partes es

{displaystyle I=int e^{x}cos(x) dx.}

Aquí, la integración por partes se realiza dos veces. Primero deja

{displaystyle u=cos(x) Rightarrow du=-sin(x) dx}

{displaystyle dv=e^{x} dx Rightarrow v=int e^{x} dx=e^{x}}

entonces:

{displaystyle int e^{x}cos(x) dx=e^{x}cos(x)+int e^{x}sin(x) dx.}

Ahora, para evaluar la integral restante, usamos de nuevo la integración por partes, con:

{displaystyle u=sin(x) Rightarrow du=cos(x) dx}

{displaystyle dv=e^{x} dx Rightarrow v=int e^{x} dx=e^{x}.}

Entonces:

{displaystyle int e^{x}sin(x) dx=e^{x}sin(x)-int e^{x}cos(x) dx.}

Poniéndolos juntos,

{displaystyle int e^{x}cos(x) dx=e^{x}cos(x)+e^{x}sin(x)-int e^{x}cos(x) dx.}

La misma integral aparece en ambos lados de esta ecuación. La integral simplemente se puede sumar a ambos lados para obtener

{displaystyle 2int e^{x}cos(x) dx=e^{x}{bigl [}sin(x)+cos(x){bigr ]}+C,}

que se reorganiza a

{displaystyle int e^{x}cos(x) dx={frac {1}{2}}e^{x}{bigl [}sin(x)+cos(x){bigr ]}+C'}

donde nuevamente C (y C′ = C/2) es una constante de integración.

Se usa un método similar para encontrar la integral de la secante al cubo.

Funciones multiplicadas por la unidad

Otros dos ejemplos bien conocidos son cuando la integración por partes se aplica a una función expresada como un producto de 1 y sí mismo. Esto funciona si se conoce la derivada de la función y también se conoce la integral de esta derivada multiplicada por x.

El primer ejemplo es ∫ ln(x) dx. Escribimos esto como:

{displaystyle I=int ln(x)cdot 1 dx.}

Sea:

{displaystyle u=ln(x) Rightarrow du={frac {dx}{x}}}

{displaystyle dv=dx Rightarrow v=x}

entonces:

{displaystyle {begin{aligned}int ln(x) dx&=xln(x)-int {frac {x}{x}} dx\&=xln(x)-int 1 dx\&=xln(x)-x+Cend{aligned}}}

donde C es la constante de integración.

El segundo ejemplo es la función tangente inversa arctan(x):

{displaystyle I=int arctan(x) dx.}

Reescribe esto como

{displaystyle int arctan(x)cdot 1 dx.}

Ahora deja:

{displaystyle u=arctan(x) Rightarrow du={frac {dx}{1+x^{2}}}}

{displaystyle dv=dx Rightarrow v=x}

entonces

{displaystyle {begin{aligned}int arctan(x) dx&=xarctan(x)-int {frac {x}{1+x^{2}}} dx\[8pt]&=xarctan(x)-{frac {ln(1+x^{2})}{2}}+Cend{aligned}}}

utilizando una combinación del método de la regla de la cadena inversa y la condición integral del logaritmo natural.

Regla LIATE

Se ha propuesto una regla general, consistente en elegir como u la función que aparece en primer lugar en la siguiente lista:

L – funciones logarítmicas:

{displaystyle ln(x), log _{b}(x),}

etc.

I – funciones trigonométricas inversas (incluyendo análogos hiperbólicos):

{displaystyle arctan(x), operatorname {arcsec}(x), operatorname {arsinh} (x),}

etc.

A – funciones algebraicas:

{displaystyle x^{2}, 3x^{50},}

etc.

T – funciones trigonométricas (incluyendo análogos hiperbólicos):

{displaystyle sin(x), tan(x), operatorname {sech} (x),}

etc.

E – funciones exponenciales:

{displaystyle e^{x}, 19^{x},}

etc.

La función que va a ser dv es la última en la lista. La razón es que las funciones inferiores en la lista generalmente tienen antiderivadas más fáciles que las funciones superiores. La regla a veces se escribe como "DETALLE" donde D representa dv y la parte superior de la lista es la función elegida para ser dv.

Para demostrar la regla LIATE, considere la integral

{displaystyle int xcdot cos(x),dx.}

Siguiendo la regla LIATE, u = x, y dv = cos(x) dx, por lo tanto du = dx, y v = sin(x), lo que hace que el convertirse en integral

{displaystyle xcdot sin(x)-int 1sin(x),dx,}

que es igual

{displaystyle xcdot sin(x)+cos(x)+C.}

En general, se intenta elegir u y dv de modo que du sea más simple que u y dv es fácil de integrar. Si en cambio se eligiera cos(x) como u, y xdx como dv, tendríamos la integral

{displaystyle {frac {x^{2}}{2}}cos(x)+int {frac {x^{2}}{2}}sin(x),dx,}

que, después de la aplicación recursiva de la fórmula de integración por partes, resultaría claramente en una recursividad infinita y no conduciría a ninguna parte.

Aunque es una regla general útil, existen excepciones a la regla de LIATE. Una alternativa común es considerar las reglas en el "ILATE" ordenar en su lugar. Además, en algunos casos, los términos polinómicos deben dividirse de formas no triviales. Por ejemplo, para integrar

{displaystyle int x^{3}e^{x^{2}},dx,}

uno establecería

{displaystyle u=x^{2},quad dv=xcdot e^{x^{2}},dx,}

para que

{displaystyle du=2x,dx,quad v={frac {e^{x^{2}}}{2}}.}

Entonces

{displaystyle int x^{3}e^{x^{2}},dx=int left(x^{2}right)left(xe^{x^{2}}right),dx=int u,dv=uv-int v,du={frac {x^{2}e^{x^{2}}}{2}}-int xe^{x^{2}},dx.}

Finalmente, esto da como resultado

{displaystyle int x^{3}e^{x^{2}},dx={frac {e^{x^{2}}left(x^{2}-1right)}{2}}+C.}

La integración por partes se usa a menudo como una herramienta para probar teoremas en el análisis matemático.

Producto Wallis

El producto Wallis infinito para $pi$

{displaystyle {begin{aligned}{frac {pi }{2}}&=prod _{n=1}^{infty }{frac {4n^{2}}{4n^{2}-1}}=prod _{n=1}^{infty }left({frac {2n}{2n-1}}cdot {frac {2n}{2n+1}}right)\[6pt]&={Big (}{frac {2}{1}}cdot {frac {2}{3}}{Big)}cdot {Big (}{frac {4}{3}}cdot {frac {4}{5}}{Big)}cdot {Big (}{frac {6}{5}}cdot {frac {6}{7}}{Big)}cdot {Big (}{frac {8}{7}}cdot {frac {8}{9}}{Big)}cdot ;cdots end{aligned}}}

puede derivarse usando integración por partes.

Identidad de la función gamma

La función gamma es un ejemplo de una función especial, definida como una integral inadecuada para $0}" xmlns="http://www.w3.org/1998/Math/MathML">z■0{displaystyle z]0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0f44149d6ef295968e2c1d391c2f98c1da9fca30" style="vertical-align: -0.338ex; width:5.349ex; height:2.176ex;"/>$ . La integración por partes ilustra que es una ampliación de la función factorial:

{displaystyle {begin{aligned}Gamma (z)&=int _{0}^{infty }e^{-x}x^{z-1}dx\[6pt]&=-int _{0}^{infty }x^{z-1},dleft(e^{-x}right)\[6pt]&=-{Biggl [}e^{-x}x^{z-1}{Biggl ]}_{0}^{infty }+int _{0}^{infty }e^{-x}dleft(x^{z-1}right)\[6pt]&=0+int _{0}^{infty }left(z-1right)x^{z-2}e^{-x}dx\[6pt]&=(z-1)Gamma (z-1).end{aligned}}}

Desde

{displaystyle Gamma (1)=int _{0}^{infty }e^{-x},dx=1,}

cuando $z$ es un número natural, es decir, ${displaystyle z=nin mathbb {N} }$ , aplicar esta fórmula repetidamente da el factorial: ${displaystyle Gamma (n+1)=n!}$

Uso en análisis armónico

La integración por partes se usa a menudo en el análisis armónico, particularmente en el análisis de Fourier, para mostrar que las integrales que oscilan rápidamente con integrandos lo suficientemente suaves decaen rápidamente. El ejemplo más común de esto es su uso para mostrar que el decaimiento de la transformada de Fourier de la función depende de la suavidad de esa función, como se describe a continuación.

Transformada de Fourier de la derivada

Si f es una función diferenciable continuamente k veces y todas las derivadas hasta la késima decaen a cero en el infinito, entonces su transformada de Fourier satisface

({mathcal {F}}f^{(k)})(xi)=(2pi ixi)^{k}{mathcal {F}}f(xi),

donde f^(k) es la késima derivada de f. (La constante exacta de la derecha depende de la convención de la transformada de Fourier utilizada). Esto se prueba observando que

{frac {d}{dy}}e^{-2pi iyxi }=-2pi ixi e^{-2pi iyxi },

entonces usando la integración por partes en la transformada de Fourier de la derivada obtenemos

{displaystyle {begin{aligned}({mathcal {F}}f')(xi)&=int _{-infty }^{infty }e^{-2pi iyxi }f'(y),dy\&=left[e^{-2pi iyxi }f(y)right]_{-infty }^{infty }-int _{-infty }^{infty }(-2pi ixi e^{-2pi iyxi })f(y),dy\[5pt]&=2pi ixi int _{-infty }^{infty }e^{-2pi iyxi }f(y),dy\[5pt]&=2pi ixi {mathcal {F}}f(xi).end{aligned}}}

Aplicando esto de forma inductiva se obtiene el resultado de k general. Se puede usar un método similar para encontrar la transformada de Laplace de una derivada de una función.

Desintegración de la transformada de Fourier

El resultado anterior nos habla del decaimiento de la transformada de Fourier, ya que se sigue que si f y f^(k) son integrables entonces

{displaystyle vert {mathcal {F}}f(xi)vert leq {frac {I(f)}{1+vert 2pi xi vert ^{k}}},{text{ where }}I(f)=int _{-infty }^{infty }{Bigl (}vert f(y)vert +vert f^{(k)}(y)vert {Bigr)},dy.}

En otras palabras, si f satisface estas condiciones, entonces su transformada de Fourier decae en el infinito al menos tan rápido como 1/|ξ |^k. En particular, si k ≥ 2 entonces la transformada de Fourier es integrable.

La prueba utiliza el hecho, que es inmediato a partir de la definición de la transformada de Fourier, que

vert {mathcal {F}}f(xi)vert leq int _{-infty }^{infty }vert f(y)vert ,dy.

Usando la misma idea sobre la igualdad establecida al comienzo de esta subsección se obtiene

vert (2pi ixi)^{k}{mathcal {F}}f(xi)vert leq int _{-infty }^{infty }vert f^{(k)}(y)vert ,dy.

Sumar estas dos desigualdades y luego dividir por 1 + |2 $π$ ξ^k| da la desigualdad indicada.

Uso en teoría de operadores

Un uso de la integración por partes en la teoría de operadores es que muestra que −∆ (donde ∆ es el operador de Laplace) es un operador positivo en L² (ver espacio Lp). Si f es uniforme y tiene un soporte compacto, entonces, usando la integración por partes, tenemos

{displaystyle {begin{aligned}langle -Delta f,frangle _{L^{2}}&=-int _{-infty }^{infty }f''(x){overline {f(x)}},dx\[5pt]&=-left[f'(x){overline {f(x)}}right]_{-infty }^{infty }+int _{-infty }^{infty }f'(x){overline {f'(x)}},dx\[5pt]&=int _{-infty }^{infty }vert f'(x)vert ^{2},dxgeq 0.end{aligned}}}

Otras aplicaciones

Determinación de las condiciones límite en la teoría de Sturm-Liouville
Conducir la ecuación Euler-Lagrange en el cálculo de variaciones

Integración repetida por partes

Considerando un segundo derivado de $v$ in the integral on the LHS of the formula for partial integration suggests a repeated application to the integral on the RHS:

{displaystyle int uv'',dx=uv'-int u'v',dx=uv'-left(u'v-int u''v,dxright).}

Extender este concepto de integración parcial repetida a derivadas de grado $n$ conduce a

{displaystyle {begin{aligned}int u^{(0)}v^{(n)},dx&=u^{(0)}v^{(n-1)}-u^{(1)}v^{(n-2)}+u^{(2)}v^{(n-3)}-cdots +(-1)^{n-1}u^{(n-1)}v^{(0)}+(-1)^{n}int u^{(n)}v^{(0)},dx.\[5pt]&=sum _{k=0}^{n-1}(-1)^{k}u^{(k)}v^{(n-1-k)}+(-1)^{n}int u^{(n)}v^{(0)},dx.end{aligned}}}

Este concepto puede ser útil cuando las sucesivas integrales de ${displaystyle v^{(n)}}$ están disponibles fácilmente (por ejemplo, exponenciales simples o sine y cosine, como en Laplace o Fourier transforma), y cuando el $n$ th derivative of $u$ desaparece (por ejemplo, como función polinomial con grado $(n-1)$ ). Esta última condición detiene la repetición de la integración parcial, porque el RHS-integral desaparece.

En el curso de la repetición anterior de integraciones parciales, las integrales

{displaystyle int u^{(0)}v^{(n)},dxquad }

{displaystyle quad int u^{(ell)}v^{(n-ell)},dxquad }

{displaystyle quad int u^{(m)}v^{(n-m)},dxquad {text{ for }}1leq m,ell leq n}

relacionarse. Esto puede interpretarse como derivaciones arbitrariamente "injertos" entre $v$ y $u$ dentro del integrado, y resulta útil, también (ver fórmula de Rodrigues).

Integración tabular por partes

El proceso esencial de la fórmula anterior se puede resumir en una tabla; el método resultante se llama "integración tabular" y apareció en la película Stand and Deliver (1988).

Por ejemplo, considere la integral

{displaystyle int x^{3}cos x,dxquad }

y tomar

{displaystyle quad u^{(0)}=x^{3},quad v^{(n)}=cos x.}

Comienzo de la lista en la columna A la función ${displaystyle u^{(0)}=x^{3}}$ y sus derivados posteriores ${displaystyle u^{(i)}}$ hasta llegar a cero. Luego lista en la columna B la función ${displaystyle v^{(n)}=cos x}$ y sus integrantes posteriores ${displaystyle v^{(n-i)}}$ hasta el tamaño de la columna B es el mismo que el de la columna A. El resultado es el siguiente:

# i	Signatura	A: derivados u⁽⁾ⁱ⁾	B: integrales v⁽⁾ⁿ⁻ⁱ⁾
0	+	$x^{3}$	$cos x$
1	−	$3x^2$	$sin x$
2	+	${displaystyle 6x}$	${displaystyle -cos x}$
3	−	$6$	${displaystyle -sin x}$
4	+	${displaystyle 0}$	$cos x$

El producto de las entradas en la fila $i$ de las columnas A y B junto con el signo respectivo dan las integrales relevantes en paso $i$ en el curso de repetidas integraciones por partes. Paso $i = 0$ genera la integral original. Para obtener el resultado completo en paso $i > 0$ la $i$ ésima integral debe ser añadido a todos los productos anteriores ( $0 \leq j < i$ ) de la $j$ ésima entrada de la columna A y $(j + 1)$ st entrada de la columna B (es decir, multiplicar la 1.ª entrada de la columna A con la 2.ª entrada de la columna B, la 2.ª entrada de la columna A con la tercera entrada de la columna B, etc....) con la $j$ th dada signo. Este proceso llega a un alto natural, cuando el producto, que produce la integral, es cero ( $i = 4$ en el ejemplo). El resultado completo es el siguiente (con los signos alternos en cada término):

{displaystyle underbrace {(+1)(x^{3})(sin x)} _{j=0}+underbrace {(-1)(3x^{2})(-cos x)} _{j=1}+underbrace {(+1)(6x)(-sin x)} _{j=2}+underbrace {(-1)(6)(cos x)} _{j=3}+underbrace {int (+1)(0)(cos x),dx} _{i=4:;to ;C}.}

Esto produce

{displaystyle underbrace {int x^{3}cos x,dx} _{text{step 0}}=x^{3}sin x+3x^{2}cos x-6xsin x-6cos x+C.}

La integración parcial repetida también resulta útil, cuando en el curso de diferenciación e integración respectivamente de las funciones ${displaystyle u^{(i)}}$ y ${displaystyle v^{(n-i)}}$ sus resultados de producto en un múltiples de los componentes originales. En este caso la repetición también puede ser terminada con este índice $i.$ Esto puede suceder, probablemente, con exponenciales y funciones trigonométricas. Como ejemplo, considere

int e^{x}cos x,dx.

# i	Signatura	A: derivados u⁽⁾ⁱ⁾	B: integrales v⁽⁾ⁿ⁻ⁱ⁾
0	+	$e^{x}$	$cos x$
1	−	$e^{x}$	$sin x$
2	+	$e^{x}$	${displaystyle -cos x}$

En este caso, el producto de los términos de las columnas A y B con el signo apropiado para el índice $i = 2$ produce el negativo del integrando original (compare filas $i = 0$ y $i = 2$ ).

{displaystyle underbrace {int e^{x}cos x,dx} _{text{step 0}}=underbrace {(+1)(e^{x})(sin x)} _{j=0}+underbrace {(-1)(e^{x})(-cos x)} _{j=1}+underbrace {int (+1)(e^{x})(-cos x),dx} _{i=2}.}

Observando que la parte integral de la RHS puede tener su propia constante de integración $C'$ , y traer la integral abstracta al otro lado, da

{displaystyle 2int e^{x}cos x,dx=e^{x}sin x+e^{x}cos x+C',}

y finalmente:

{displaystyle int e^{x}cos x,dx={frac {1}{2}}left(e^{x}(sin x+cos x)right)+C,}

donde C = C′/2.

Dimensiones superiores

La integración por partes se puede extender a funciones de varias variables aplicando una versión del teorema fundamental del cálculo a una regla de producto apropiada. Hay varios emparejamientos de este tipo posibles en el cálculo multivariado, que involucran una función con valores escalares u y una función con valores vectoriales (campo vectorial) V.

La regla del producto para la divergencia establece:

{displaystyle nabla cdot (umathbf {V}) = u,nabla cdot mathbf {V} + nabla ucdot mathbf {V}.}

Suppose $Omega$ es un subconjunto atado abierto $mathbb {R} ^{n}$ con un borde liso ${displaystyle Gamma =partial Omega }$ . Integración $Omega$ con respecto al formulario de volumen estándar $dOmega$ , y aplicando el teorema de divergencia, da:

{displaystyle int _{Gamma }umathbf {V} cdot {hat {mathbf {n} }},dGamma = int _{Omega }nabla cdot (umathbf {V}),dOmega = int _{Omega }u,nabla cdot mathbf {V} ,dOmega + int _{Omega }nabla ucdot mathbf {V} ,dOmega}

Donde ${displaystyle {hat {mathbf {n} }}}$ es la unidad exterior vector normal a la frontera, integrado con respecto a su forma de volumen Riemanniano estándar $dGamma$ . Reorganizar da:

{displaystyle int _{Omega }u,nabla cdot mathbf {V} ,dOmega = int _{Gamma }umathbf {V} cdot {hat {mathbf {n} }},dGamma -int _{Omega }nabla ucdot mathbf {V} ,dOmega}

o en otras palabras

{displaystyle int _{Omega }u,operatorname {div} (mathbf {V}),dOmega = int _{Gamma }umathbf {V} cdot {hat {mathbf {n} }},dGamma -int _{Omega }operatorname {grad} (u)cdot mathbf {V} ,dOmega.}

{displaystyle Gamma =partial Omega }

uvH¹

Primera identidad de Green

Considere los campos vectoriales continuamente diferenciables ${displaystyle mathbf {U} =u_{1}mathbf {e} _{1}+cdots +u_{n}mathbf {e} _{n}}$ y ${displaystyle vmathbf {e} _{1},ldotsvmathbf {e} _{n}}$ , donde $mathbf {e} _{i}$ es i-th standard basis vector for $i=1,ldotsn$ . Ahora aplicar la integración anterior por partes a cada $u_{i}$ tiempos el campo vectorial ${displaystyle vmathbf {e} _{i}}$ :

{displaystyle int _{Omega }u_{i}{frac {partial v}{partial x_{i}}},dOmega = int _{Gamma }u_{i}v,mathbf {e} _{i}cdot {hat {mathbf {n} }},dGamma -int _{Omega }{frac {partial u_{i}}{partial x_{i}}}v,dOmega.}

Sumar sobre i da una nueva fórmula de integración por partes:

{displaystyle int _{Omega }mathbf {U} cdot nabla v,dOmega = int _{Gamma }vmathbf {U} cdot {hat {mathbf {n} }},dGamma -int _{Omega }v,nabla cdot mathbf {U} ,dOmega.}

El caso ${displaystyle mathbf {U} =nabla u}$ , donde ${displaystyle uin C^{2}({bar {Omega }})}$ , se conoce como la primera de las identidades de Green:

{displaystyle int _{Omega }nabla ucdot nabla v,dOmega = int _{Gamma }v,nabla ucdot {hat {mathbf {n} }},dGamma -int _{Omega }v,nabla ^{2}u,dOmega.}

Contenido relacionado

Más resultados...