Integracion numerica

La integración numérica se utiliza para calcular una aproximación numérica para el valor S{displaystyle S., el área bajo la curva definida por f()x){displaystyle f(x)}.

En análisis, la integración numérica comprende una amplia familia de algoritmos para calcular el valor numérico de una integral definida y, por extensión, el término también se usa a veces para describir la solución numérica de ecuaciones diferenciales. Este artículo se centra en el cálculo de integrales definidas.

El término cuadratura numérica (a menudo abreviado como cuadratura) es más o menos un sinónimo de integración numérica, especialmente cuando se aplica a integrales unidimensionales. Algunos autores se refieren a la integración numérica sobre más de una dimensión como cubatura; otros toman cuadratura para incluir integración de dimensiones superiores.

El problema básico en la integración numérica es calcular una solución aproximada para una integral definida

∫ ∫ abf()x)dx{displaystyle int _{a} {b}f(x),dx}

hasta un determinado grado de precisión. Si f(x) es una función suave integrada en un pequeño número de dimensiones, y el dominio de integración está acotado, hay muchos métodos para aproximar la integral a la precisión deseada.

Razones para la integración numérica

Hay varias razones para llevar a cabo la integración numérica, a diferencia de la integración analítica mediante la búsqueda de la antiderivada:

1. El componente f()x) puede ser conocido sólo en ciertos puntos, como obtenido por muestreo. Algunos sistemas integrados y otras aplicaciones informáticas pueden necesitar integración numérica por esta razón.
2. Una fórmula para el integrador puede ser conocida, pero puede ser difícil o imposible encontrar un antiderivativo que es una función elemental. Un ejemplo de tal componente es f()x) = exp(−x²), el antiderivativo de que (la función de error, tiempos una constante) no puede ser escrito en forma elemental.
3. Puede ser posible encontrar un antiderivativo simbólicamente, pero puede ser más fácil calcular una aproximación numérica que calcular el antiderivativo. Ese puede ser el caso si el antiderivativo se da como una serie o producto infinito, o si su evaluación requiere una función especial que no está disponible.

Historia

El término "integración numérica" aparece por primera vez en 1915 en la publicación Un curso de interpolación e integración numérica para el laboratorio matemático de David Gibb.

Cuadratura es un término matemático histórico que significa área de cálculo. Los problemas de cuadratura han servido como una de las principales fuentes de análisis matemático. Los matemáticos de la Antigua Grecia, según la doctrina pitagórica, entendían el cálculo de área como el proceso de construir geométricamente un cuadrado de igual área (cuadrar). Por eso el proceso se denominó cuadratura. Por ejemplo, una cuadratura del círculo, Luna de Hipócrates, La cuadratura de la parábola. Esta construcción debe realizarse únicamente por medio de compás y regla.

Los antiguos babilonios usaban la regla trapezoidal para integrar el movimiento de Júpiter a lo largo de la eclíptica.

Método antiguo para encontrar la media geométrica

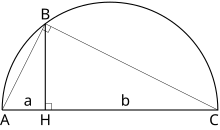
Para una cuadratura de un rectángulo con los lados a y b es necesario construir un cuadrado con el lado x=ab{displaystyle x={sqrt {ab}} (la media geométrica de a y b). Para ello es posible utilizar el siguiente hecho: si dibujamos el círculo con la suma de a y b como el diámetro, entonces la altura BH (desde un punto de su conexión a cruzar con un círculo) equivale a su media geométrica. La construcción geométrica similar resuelve un problema de una cuadratura para un paralelograma y un triángulo.

El área de un segmento de una parabola

Los problemas de cuadratura para figuras curvilíneas son mucho más difíciles. La cuadratura del círculo con compás y regla se demostró en el siglo XIX que era imposible. Sin embargo, para algunas figuras (por ejemplo, la Luna de Hipócrates) se puede realizar una cuadratura. Las cuadraturas de una superficie esférica y un segmento de parábola realizadas por Arquímedes se convirtieron en el mayor logro del análisis antiguo.

• El área de la superficie de una esfera es igual a cuadruplicar el área de un gran círculo de esta esfera.
• El área de un segmento de la parabola cortada por una línea recta es 4/3 el área del triángulo inscrito en este segmento.

Para la prueba de los resultados Arquímedes utilizó el Método de agotamiento de Eudoxo.

En la Europa medieval, la cuadratura significaba el cálculo del área por cualquier método. Más a menudo se utilizó el Método de los indivisibles; era menos riguroso, pero más simple y poderoso. Con su ayuda, Galileo Galilei y Gilles de Roberval encontraron el área de un arco cicloide, Grégoire de Saint-Vincent investigó el área bajo una hipérbola (Opus Geometricum, 1647), y Alphonse Antonio de Sarasa, de Saint -El alumno y comentarista de Vincent, notó la relación de esta área con los logaritmos.

John Wallis algebrizó este método: escribió en su serie Arithmetica Infinitorum (1656) que ahora llamamos integral definida, y calculó sus valores. Isaac Barrow y James Gregory hicieron más progresos: cuadraturas para algunas curvas y espirales algebraicas. Christiaan Huygens realizó con éxito una cuadratura de algunos Sólidos de revolución.

La cuadratura de la hipérbola de Saint-Vincent y de Sarasa proporcionó una nueva función, el logaritmo natural, de importancia crítica.

Con la invención del cálculo integral surgió un método universal para el cálculo de áreas. En respuesta, el término cuadratura se ha vuelto tradicional y, en su lugar, la frase moderna "cálculo de una integral definida univariada" Es más común.

Métodos para integrales unidimensionales

Los métodos de integración numérica generalmente se pueden describir como la combinación de evaluaciones del integrando para obtener una aproximación a la integral. El integrando se evalúa en un conjunto finito de puntos denominados puntos de integración y se utiliza una suma ponderada de estos valores para aproximar la integral. Los puntos de integración y los pesos dependen del método específico utilizado y la precisión requerida de la aproximación.

Una parte importante del análisis de cualquier método de integración numérica es estudiar el comportamiento del error de aproximación en función del número de evaluaciones integrando. Un método que arroja un pequeño error para un pequeño número de evaluaciones generalmente se considera superior. Reducir el número de evaluaciones del integrando reduce el número de operaciones aritméticas involucradas y, por lo tanto, reduce el error de redondeo total. Además, cada evaluación lleva tiempo y el integrando puede ser arbitrariamente complicado.

Una 'fuerza bruta' Se puede hacer un tipo de integración numérica, si el integrando tiene un comportamiento razonablemente bueno (es decir, continuo por partes y de variación acotada), evaluando el integrando con incrementos muy pequeños.

Reglas de cuadratura basadas en funciones de interpolación

Se puede derivar una gran clase de reglas de cuadratura mediante la construcción de funciones de interpolación que son fáciles de integrar. Por lo general, estas funciones de interpolación son polinomios. En la práctica, dado que los polinomios de grado muy alto tienden a oscilar mucho, solo se utilizan polinomios de grado bajo, normalmente lineales y cuadráticos.

Ilustración de la regla del rectángulo.

El método más simple de este tipo es permitir que la función interpoladora sea una función constante (un polinomio de grado cero) que pasa por el punto ()a+b2,f()a+b2)){textstyle left({frac {a+b}{2},fleft({frac} {a+b}{2}right)right)}. Esto se llama Regla de punto medio o regla del rectángulo

∫ ∫ abf()x)dx.. ()b− − a)f()a+b2).{displaystyle int _{a}^{b}f(x),dxapprox (b-a)fleft({frac {a+b}{2}right).}

Ilustración de la regla trapezoidal.

La función de interpolación puede ser una línea recta (una función afine, es decir, un polinomio de grado 1) pasando por los puntos ()a,f()a)){displaystyle left(a,f(a)right)} y ()b,f()b)){displaystyle left(b,f(b)right)}. Esto se llama Regla trapezoidal

∫ ∫ abf()x)dx.. ()b− − a)()f()a)+f()b)2).{displaystyle int _{a}^{b}f(x),dxapprox (b-a)left({frac {f(a)+f(b)}{2}right).}

Ilustración de la regla de Simpson.

Para cualquiera de estas reglas, podemos hacer una aproximación más precisa rompiendo el intervalo [a,b]{displaystyle [a,b]} en algunos números n{displaystyle n} de subintervalos, calculando una aproximación para cada subintervalo, añadiendo todos los resultados. Esto se llama norma compuesta, Regla ampliada, o regla iterada. Por ejemplo, la regla trapezoidal compuesta puede ser declarada como

∫ ∫ abf()x)dx.. b− − an()f()a)2+.. k=1n− − 1()f()a+kb− − an))+f()b)2),{displaystyle int _{a}^{b}f(x),dxapprox {frac {b-a}{n}left({f(a) over 2}+sum _{k=1}^{n-1}left(fleft(a+k{frac {b-a}{n}right)+{f(b) over 2}right),}

donde los subintervalos tienen la forma [a+kh,a+()k+1)h]⊂ ⊂ [a,b],{displaystyle [a+kh,a+(k+1)h]subset [a,b],} con h=b− − an{textstyle h={frac {B-a}{n}} y k=0,...... ,n− − 1.{displaystyle k=0,ldotsn-1.} Aquí usamos subintervalos de la misma longitud h{displaystyle h} pero también se podría utilizar intervalos de longitud variable ()hk)k{displaystyle left(h_{k}right)_{k}.

Interpolación con polinomios evaluados en puntos igualmente espaciados en [a,b]{displaystyle [a,b]} cede las fórmulas Newton-Cotes, de las cuales la regla del rectángulo y la regla trapezoidal son ejemplos. La regla de Simpson, que se basa en un polinomio del orden 2, es también una fórmula Newton-Cotes.

Las reglas de cuadratura con puntos igualmente espaciados tienen la propiedad muy conveniente de anidamiento. La regla correspondiente con cada intervalo subdividido incluye todos los puntos actuales, por lo que esos valores de integrando se pueden reutilizar.

Si permitimos que varíen los intervalos entre los puntos de interpolación, encontramos otro grupo de fórmulas de cuadratura, como las fórmulas de cuadratura gaussiana. Una regla de cuadratura gaussiana suele ser más precisa que una regla de Newton-Cotes que usa el mismo número de evaluaciones de función, si el integrando es suave (es decir, si es lo suficientemente diferenciable). Otros métodos de cuadratura con intervalos variables incluyen los métodos de cuadratura de Clenshaw-Curtis (también llamados cuadratura de Fejér), que se anidan.

Las reglas de cuadratura de Gauss no anidan, pero sí las fórmulas de cuadratura de Gauss-Kronrod relacionadas.

Fórmula de la regla del punto medio generalizada

La fórmula de la regla del punto medio generalizada viene dada por

∫ ∫ 01f()x)dx=.. m=1M.. n=0JUEGO JUEGO ()− − 1)n+1()2M)n+1()n+1)!f()n)()x)Silenciox=m− − 1/2M{displaystyle int _{0}^{1}f(x),dx=sum ¿Qué? {fn=0}{infty}{frac {left({-1}right)}{n}+1}{left(2Mright)^{n+1}left({n+1}right)}{left.f^{(n)}(x)}{x={frac={n=0} {m-1/2} {M}}}}}

∫ ∫ 01f()x)dx=limN→ → JUEGO JUEGO .. m=1M.. n=0N()− − 1)n+1()2M)n+1()n+1)!f()n)()x)Silenciox=m− − 1/2M,{displaystyle int _{0}{1}{f(x),dx}=lim _{Nto infty }sum ¿Qué? {fn0}{n}{m}}} {n+1}}}{n}}{left({2M}right)}} {n+1}left({n+1}right)}{left.f^{(n)}(x)derecho)}{x={n=frac=0}{n=0}}}}}{n}}}}{n}}{n}{n}}{n}{n}{n}{n}}{n}{n}n}n}{n}{n}}}}}n}n}{n}{n}{n}{n}n}n}n}n}{n}n}{n}n}n}n}n}n}n}n}n}n}}n}n}}n}}}}}} ♪♪

f()n)()x){displaystyle f^{(n)}(x)}

n{displaystyle n}

M=1{displaystyle M=1}

f()x)=Silencio Silencio 1+Silencio Silencio 2x2{displaystyle f(x)={frac {theta }{1+theta ^{2}x^{2}}}

#− − 1⁡ ⁡ ()Silencio Silencio )=i.. n=1JUEGO JUEGO 12n− − 1()1()1+2i/Silencio Silencio )2n− − 1− − 1()1− − 2i/Silencio Silencio )2n− − 1)=2.. n=1JUEGO JUEGO 12n− − 1an()Silencio Silencio )an2()Silencio Silencio )+bn2()Silencio Silencio ),{fn0} {fn0} {fn0} {fn0} {fn0} {fn1}n1}}n1}nn1}ln}nnnccn1} {fn1} {fn1} {fn1} {fn1} {fn1}n1} {n1}fn0} {ssssssssssssssssigualto}}nssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss00}fnnnnnnnnnnnnnnnnnnnn ¿Por qué? }

i=− − 1{displaystyle i={sqrt {-1}

a1()Silencio Silencio )=2Silencio Silencio ,b1()Silencio Silencio )=1,an()Silencio Silencio )=()1− − 4Silencio Silencio 2)an− − 1()Silencio Silencio )+4Silencio Silencio bn− − 1()Silencio Silencio ),bn()Silencio Silencio )=()1− − 4Silencio Silencio 2)bn− − 1()Silencio Silencio )− − 4Silencio Silencio an− − 1()Silencio Silencio ).{fnMicrosoft Sans Ser) {fnMicrosoft Sans Serif} {fn]}b_{1}(theta)} {fn} {fn} {fn} {fn} {fnMicrosoft ] {c} {fn0} {fnMicroc} {c} {fnMicrosoft}}} {fn}}}}}}fn} {c}}fn}f}f}f}f}cf}f}ccf}cfnf}fnf}cf}f}cfnf}cccccfn}cccccccccfn}fnun}cccccccccccccc}cc ################################################################################################################################################################################################################################################################ {4}{theta },a_{n-1}(theta)end{aligned}}

Desde cada punto de vista n{displaystyle n} el numerador del componente se convierte en ()− − 1)n+1=0{displaystyle (-1)}{n}+1=0}, la fórmula generalizada de la regla de punto medio se puede reorganizar como

∫ ∫ 01f()x)dx=2.. m=1M.. n=0JUEGO JUEGO 1()2M)2n+1()2n+1)!f()2n)()x)Silenciox=m− − 1/2M.{displaystyle int _{0}^{1}f(x),dx=2sum ¿Qué? {fn=0}{infty }{frac {1}{left(2Mright)^{2n+1}}left({2n+1}right)}{left.f^{(2n)}(x)right}_{x={frac={frac {m-1/2} {M}}},,}

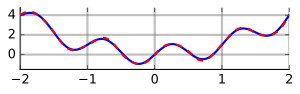
El siguiente ejemplo del código Mathematica genera la diferencia de trama entre el tangente inverso y su aproximación truncada a M=5{displaystyle M=5} y N=10{displaystyle N=10}:

f[theta_, x_] := theta/()1 + theta^2 * x^2);aTan[theta_, M_, nMax_] :=  2*Sum[Función[x, Evaluate[D[f[theta, x] {}x, 2*n[ ]] [m - 1/2)/ M])/()2*n + 1)! *()2*M)^()2*n + 1)), {}m, 1, M} {}n, 0, nMax}]Parcela[ {}ArcTan[theta] - aTan[theta, 5, 10] {}theta, -Pi, Pi}  PlotRange - Todos]

Para una función g()t){displaystyle g(t)} definido a intervalos ()a,b){displaystyle (a,b)}, su integral es

∫ ∫ abg()t)dt=∫ ∫ 0b− − ag()τ τ +a)dτ τ =()b− − a)∫ ∫ 01g()()b− − a)x+a)dx.{displaystyle int _{a}^{b}g(t),dt=int _{0}^{b-a}g(tau +a),dtau =(b-a)int _{0}{1}g(b-a)x+a),dx.}

f()x)=()b− − a)g()()b− − a)x+a){displaystyle f(x)=(b-a),g(b-a)x+a)}

Algoritmos adaptativos

Si f(x) no tiene muchas derivadas en todos los puntos, o si las derivadas se vuelven grandes, entonces la cuadratura gaussiana suele ser insuficiente. En este caso, un algoritmo similar al siguiente funcionará mejor:

def calculate_definite_integral_of_f()f, inicial_step_size) - flotador: " Este algoritmo calcula la parte integral definida de una función de 0 a 1, adaptablemente, eligiendo pasos más pequeños cerca puntos problemáticos. " x = 0,0 h = inicial_step_size accumulator = 0,0 mientras x . 1.0: si x + h ■ 1.0: h = 1.0 - x # Al final del intervalo de unidad, ajuste el último paso a fin a 1. si error_too_big_in_quadrature_of_f_over_range()f, [x, x + h] h = make_h_smaller()h) más: accumulator += quadrature_of_f_over_range()f, [x, x + h]) x += h si error_too_small_in_quadrature_of_over_range()f, [x, x + h] h = make_h_larger()h) # Evite perder tiempo en pequeños pasos. retorno accumulator

Algunos detalles del algoritmo requieren una cuidadosa reflexión. En muchos casos, estimar el error de cuadratura en un intervalo para una función f(x) no es obvio. Una solución popular es usar dos reglas diferentes de cuadratura y usar su diferencia como una estimación del error de cuadratura. El otro problema es decidir qué "demasiado grande" o "muy pequeño" significar. Un criterio local para "demasiado grande" es que el error de cuadratura no debe ser mayor que t ⋅ h donde t, un número real, es la tolerancia que deseamos establecer para global error. Por otra parte, si h ya es pequeño, puede que no valga la pena hacerlo aún más pequeño incluso si el error de cuadratura es aparentemente grande. Un criterio global es que la suma de errores en todos los intervalos debe ser menor que t. Este tipo de análisis de errores suele denominarse "a posteriori" ya que calculamos el error después de haber calculado la aproximación.

Forsythe et al. analizan la heurística para la cuadratura adaptativa. (Sección 5.4).

Métodos de extrapolación

La precisión de una regla de cuadratura del tipo Newton-Cotes generalmente es una función del número de puntos de evaluación. El resultado suele ser más preciso a medida que aumenta el número de puntos de evaluación o, de manera equivalente, a medida que disminuye el ancho del tamaño de paso entre los puntos. Es natural preguntarse cuál sería el resultado si se permitiera que el tamaño del paso se acercara a cero. Esto se puede responder extrapolando el resultado de dos o más tamaños de paso distintos de cero, utilizando métodos de aceleración en serie como la extrapolación de Richardson. La función de extrapolación puede ser una función polinomial o racional. Los métodos de extrapolación se describen con más detalle en Stoer y Bulirsch (Sección 3.4) y se implementan en muchas de las rutinas de la biblioteca QUADPACK.

Estimación conservadora (a priori) del error

Vamos f{displaystyle f} tener un primer derivado ligado sobre [a,b],{displaystyle [a,b],} i.e. f▪ ▪ C1()[a,b]).{displaystyle fin C^{1}([a,b]).} El valor medio teorema para f,{displaystyle f,} Donde x▪ ▪ [a,b),{displaystyle xin [a,b] da

()x− − a)f.().. x)=f()x)− − f()a),{displaystyle (x-a)f'(xi _{x})=f(x)-f(a),}

.. x▪ ▪ ()a,x]{displaystyle xi _{x}in (a,x]}

x{displaystyle x}

Si nos integramos en x{displaystyle x} desde a{displaystyle a} a b{displaystyle b} en ambos lados y tomar los valores absolutos, obtenemos

Silencio∫ ∫ abf()x)dx− − ()b− − a)f()a)Silencio=Silencio∫ ∫ ab()x− − a)f.().. x)dxSilencio.{displaystyle left WordPressint _{a}^{b}f(x),dx-(b-a)f(a)right eterna=left imperint _{a}{b}(x-a)f'(xi _{x}),dxright durable.}

Podemos aproximar aún más la integral en el lado derecho al introducir el valor absoluto en el integrado, y sustituir el término en f.{displaystyle f'} por un borde superior

Silencio∫ ∫ abf()x)dx− − ()b− − a)f()a)Silencio≤ ≤ ()b− − a)22Supa≤ ≤ x≤ ≤ bSilenciof.()x)Silencio,{displaystyle left durableint _{a}^{b}f(x),dx-(b-a)f(a)right eternaleq {(b-a)^{2}sup _{aleq xleq b}left sometidaf'(x)right,}

()1)

donde se utilizó el supremo para aproximar.

Por lo tanto, si aproximamos la integral ∫ ∫ abf()x)dx{textstyle int _{a}{b}f(x),dx} por la regla de la cuadratura ()b− − a)f()a){displaystyle (b-a)f(a)} nuestro error no es mayor que el lado derecho 1. Podemos convertir esto en un análisis de errores para la suma Riemann, dando un límite superior de

n− − 12Sup0≤ ≤ x≤ ≤ 1Silenciof.()x)Silencio{displaystyle {frac {fn}{2}sup} ¿Por qué?

f()x)=x{displaystyle f(x)=x}

Este método de integración se puede combinar con la aritmética de intervalos para producir pruebas por computadora y cálculos verificados.

Integrales sobre intervalos infinitos

Existen varios métodos para la integración aproximada en intervalos ilimitados. La técnica estándar implica reglas de cuadratura especialmente derivadas, como la cuadratura de Gauss-Hermite para integrales en toda la línea real y la cuadratura de Gauss-Laguerre para integrales en los reales positivos. También se pueden utilizar métodos de Monte Carlo, o un cambio de variables a un intervalo finito; por ejemplo, para toda la línea se podría usar

∫ ∫ − − JUEGO JUEGO JUEGO JUEGO f()x)dx=∫ ∫ − − 1+1f()t1− − t2)1+t2()1− − t2)2dt,{displaystyle int _{-infty }{infty }f(x),dx=int - ¿Qué? {T}{1-t^{2}}right){frac {1+t^{2}{left(1-t^{2}},dt,}

∫ ∫ aJUEGO JUEGO f()x)dx=∫ ∫ 01f()a+t1− − t)dt()1− − t)2,∫ ∫ − − JUEGO JUEGO af()x)dx=∫ ∫ 01f()a− − 1− − tt)dtt2,{displaystyle {begin{aligned}int _{a}{infty }f(x),dx limit=int ¿Qué? {t}{1-t}}\int _{-infty }{a}f(x),dx limit=int ¿Qué? {1-t} {}right){frac {dt}{2}}},end{aligned}}

Integrales multidimensionales

Todas las reglas de cuadratura discutidas hasta ahora están diseñadas para calcular integrales unidimensionales. Para calcular integrales en múltiples dimensiones, un enfoque es expresar la integral múltiple como integrales unidimensionales repetidas aplicando el teorema de Fubini (la regla del producto tensorial). Este enfoque requiere que las evaluaciones de funciones crezcan exponencialmente a medida que aumenta el número de dimensiones. Se conocen tres métodos para superar esta llamada maldición de la dimensionalidad.

En la monografía de Stroud se proporcionan muchas técnicas adicionales para formar reglas de integración de cubos multidimensionales para una variedad de funciones de ponderación. La integración en la esfera ha sido revisada por Hesse et al. (2015).

Montecarlo

Los métodos de Monte Carlo y los métodos cuasi-Monte Carlo son fáciles de aplicar a integrales multidimensionales. Pueden producir una mayor precisión para el mismo número de evaluaciones de funciones que las integraciones repetidas utilizando métodos unidimensionales.

Una gran clase de métodos de Monte Carlo útiles son los denominados algoritmos de Monte Carlo de cadena de Markov, que incluyen el algoritmo Metropolis-Hastings y el muestreo de Gibbs.

Rejillas dispersas

Las cuadrículas dispersas fueron desarrolladas originalmente por Smolyak para la cuadratura de funciones de alta dimensión. El método siempre se basa en una regla de cuadratura unidimensional, pero realiza una combinación más sofisticada de resultados univariados. Sin embargo, mientras que la regla del producto tensorial garantiza que los pesos de todos los puntos de cubatura serán positivos si los pesos de los puntos de cuadratura fueran positivos, la regla de Smolyak no garantiza que los pesos sean todos positivos.

Cuadratura bayesiana

La cuadratura bayesiana es un enfoque estadístico del problema numérico de calcular integrales y cae dentro del campo de la estadística numérica probabilística. Puede proporcionar un manejo completo de la incertidumbre sobre la solución de la integral expresada como una varianza posterior del proceso gaussiano.

Conexión con ecuaciones diferenciales

El problema de evaluar la integral

F()x)=∫ ∫ axf()u)du{displaystyle F(x)=int _{a}{x}f(u),du}

puede reducirse a un problema de valor inicial para una ecuación diferencial ordinaria aplicando la primera parte del teorema fundamental del cálculo. Al diferenciar ambos lados de lo anterior con respecto al argumento x, se ve que la función F satisface

dF()x)dx=f()x),F()a)=0.{displaystyle {frac {dF(x)}{dx}=f(x),quad F(a)=0.}

Los métodos desarrollados para ecuaciones diferenciales ordinarias, como los métodos de Runge-Kutta, se pueden aplicar al problema reformulado y, por lo tanto, se pueden usar para evaluar la integral. Por ejemplo, el método estándar de Runge-Kutta de cuarto orden aplicado a la ecuación diferencial produce la regla de Simpson desde arriba.

La ecuación diferencial F.()x)=f()x){displaystyle F'(x)=f(x)} tiene una forma especial: el lado derecho contiene sólo la variable independiente (aquí x{displaystyle x}) y no la variable dependiente (aquí F{displaystyle F}). Esto simplifica considerablemente la teoría y los algoritmos. Por lo tanto, el problema de la evaluación integral es mejor estudiado en su propio derecho.