Información mutua

En teoría de la probabilidad y teoría de la información, la información mutua (IM) de dos variables aleatorias es una medida de la dependencia mutua entre las dos variables. Más específicamente, cuantifica la "cantidad de información" (en unidades como shannons (bits), nats o hartleys) obtuvieron aproximadamente una variable aleatoria observando la otra variable aleatoria. El concepto de información mutua está íntimamente ligado al de entropía de una variable aleatoria, una noción fundamental en la teoría de la información que cuantifica la "cantidad de información" mantenido en una variable aleatoria.

No limitado a variables aleatorias de valor real y dependencia lineal como el coeficiente de correlación, MI es más general y determina cuán diferente es la distribución conjunta del par ()X,Y){displaystyle (X,Y)} es del producto de las distribuciones marginales de X{displaystyle X} y Y{displaystyle Sí.. MI es el valor esperado de la información mutua puntual (PMI).

La cantidad fue definida y analizada por Claude Shannon en su histórico artículo "Una teoría matemática de la comunicación", aunque no la llamó "información mutua". Este término fue acuñado posteriormente por Robert Fano. La información mutua también se conoce como ganancia de información.

Definición

Vamos ()X,Y){displaystyle (X,Y)} ser un par de variables aleatorias con valores sobre el espacio X× × Y{fnMicrosoft Sans {fnMicrosoft Sans Serif}. Si su distribución conjunta es P()X,Y){displaystyle P_{(X,Y)} y las distribuciones marginales PX{displaystyle P_{X} y PY{displaystyle P_{Y}, la información mutua se define como

Donde DKL{displaystyle D_{mathrm {KL}} es la divergencia Kullback-Leibler, y PX⊗ ⊗ PY{displaystyle P_{X}otimes P_{Y} es la distribución exterior del producto que asigna probabilidad PX()x)⋅ ⋅ PY()Sí.){displaystyle P_{X}(x)cdot P_{Y}(y)} a cada uno ()x,Sí.){displaystyle (x,y)}.

Observe, según la propiedad de la divergencia Kullback-Leibler, que I()X;Y){displaystyle I(X;Y)} es igual a cero precisamente cuando la distribución conjunta coincide con el producto de los marginales, es decir, cuando X{displaystyle X} y Y{displaystyle Sí. son independientes (y por lo tanto observan Y{displaystyle Sí. no te dice nada X{displaystyle X}). I()X;Y){displaystyle I(X;Y)} es no negativo, es una medida del precio para la codificación ()X,Y){displaystyle (X,Y)} como un par de variables independientes al azar cuando en realidad no lo son.

Si se utiliza el logaritmo natural, la unidad de información mutua es el nat. Si se utiliza el log base 2, la unidad de información mutua es el shannon, también conocido como bit. Si se utiliza el registro de base 10, la unidad de información mutua es el hartley, también conocido como ban o dit.

En términos de PMF para distribuciones discretas

La información mutua de dos variables comunes discretas al azar X{displaystyle X} y Y{displaystyle Sí. se calcula como una suma doble:

I⁡ ⁡ ()X;Y)=.. Sí.▪ ▪ Y.. x▪ ▪ XP()X,Y)()x,Sí.)log⁡ ⁡ ()P()X,Y)()x,Sí.)PX()x)PY()Sí.)),{displaystyle operatorname {I} (X;Y)=sum _{yin {mathcal {Y}}}sum _{xin {mathcal {X}}{P_{(X,Y)}(x,y)log left({frac {_{(X,Y)}(x,y)}{P_{X}(x),P_{Y}(y)}}right)}}

()Eq.1)

Donde P()X,Y){displaystyle P_{(X,Y)} es la función de masa de probabilidad conjunta X{displaystyle X} y Y{displaystyle Sí., y PX{displaystyle P_{X} y PY{displaystyle P_{Y} son las funciones de masa de probabilidad marginal X{displaystyle X} y Y{displaystyle Sí. respectivamente.

En términos de PDF para distribuciones continuas

En el caso de variables aleatorias conjuntamente continuas, la doble suma se sustituye por una doble integral:

I⁡ ⁡ ()X;Y)=∫ ∫ Y∫ ∫ XP()X,Y)()x,Sí.)log⁡ ⁡ ()P()X,Y)()x,Sí.)PX()x)PY()Sí.))dxdSí.,{fnMitcal {fnMitcal {fnMitcal {fnMitcal {fnMitcal {f} {fnMitcal} {cHFF} {cHFF} {cHFF} {cHFF} {cHFF} {ccHFF}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00cH00}cH00}cH00}cH00}cH00cH00}cH00}cH00}cH00}cH00}cH00}cH00cH00}cH00}cH00}cH00cH00}cH00}cH00cH00}}cH00}

()Eq.2)

Donde P()X,Y){displaystyle P_{(X,Y)} es ahora la probabilidad conjunta densidad función X{displaystyle X} y Y{displaystyle Sí., y PX{displaystyle P_{X} y PY{displaystyle P_{Y} son las funciones de densidad de probabilidad marginal X{displaystyle X} y Y{displaystyle Sí. respectivamente.

Motivación

Intuitivamente, la información mutua mide la X{displaystyle X} y Y{displaystyle Sí. compartir: Mide cuánto saber una de estas variables reduce la incertidumbre sobre la otra. Por ejemplo, si X{displaystyle X} y Y{displaystyle Sí. son independientes, entonces sabiendo X{displaystyle X} no da ninguna información sobre Y{displaystyle Sí. y viceversa, así que su información mutua es cero. En el otro extremo, si X{displaystyle X} es una función determinista Y{displaystyle Sí. y Y{displaystyle Sí. es una función determinista X{displaystyle X} entonces toda la información transmitida X{displaystyle X} es compartido con Y{displaystyle Sí.: sabiendo X{displaystyle X} determina el valor de Y{displaystyle Sí. y viceversa. Como resultado, en este caso la información mutua es la misma que la incertidumbre contenida en Y{displaystyle Sí. (o X{displaystyle X}) solo, es decir, la entropía de Y{displaystyle Sí. (o X{displaystyle X}). Además, esta información mutua es la misma que la entropía de X{displaystyle X} y como la entropía de Y{displaystyle Sí.. (Un caso muy especial de esto es cuando X{displaystyle X} y Y{displaystyle Sí. son la misma variable aleatoria.)

La información mutua es una medida de la dependencia inherente expresada en la distribución conjunta de X{displaystyle X} y Y{displaystyle Sí. relativa a la distribución marginal X{displaystyle X} y Y{displaystyle Sí. bajo el supuesto de independencia. Por lo tanto, la información mutua mide la dependencia en el sentido siguiente: I⁡ ⁡ ()X;Y)=0{displaystyle operatorname {I} (X;Y)=0} si X{displaystyle X} y Y{displaystyle Sí. son variables aleatorias independientes. Esto es fácil de ver en una dirección: si X{displaystyle X} y Y{displaystyle Sí. son independientes, entonces p()X,Y)()x,Sí.)=pX()x)⋅ ⋅ pY()Sí.){displaystyle p_{(X,Y)}(x,y)=p_{X}(x)cdot p_{Y}(y)}, y por lo tanto:

log⁡ ⁡ ()p()X,Y)()x,Sí.)pX()x)pY()Sí.))=log⁡ ⁡ 1=0.{displaystyle log {left({frac {p_{(X,Y)}(x,y)}{p_{X}(x),p_{Y}(y)}right)}=log 1=0.}

Además, la información mutua no es negativa (es decir, no. I⁡ ⁡ ()X;Y)≥ ≥ 0{displaystyle operatorname {I} (X;Y)geq 0} ver abajo) y simétrico (es decir, I⁡ ⁡ ()X;Y)=I⁡ ⁡ ()Y;X){displaystyle operatorname [I} (X;Y)=operatorname {I} (Y;X)} véase infra).

Propiedades

No negatividad

Usando la desigualdad de Jensen en la definición de información mutua podemos demostrar que I⁡ ⁡ ()X;Y){displaystyle operatorname {I} (X;Y)} no es negativo, es decir.

I⁡ ⁡ ()X;Y)≥ ≥ 0{displaystyle operatorname {I} (X;Y)geq 0}

Simetría

I⁡ ⁡ ()X;Y)=I⁡ ⁡ ()Y;X){displaystyle operatorname [I} (X;Y)=operatorname {I} (Y;X)}

La prueba se da considerando la relación con la entropía, como se muestra a continuación.

Supermodularidad bajo independencia

Si C{displaystyle C} es independiente de ()A,B){displaystyle (A,B)}, entonces

I⁡ ⁡ ()Y;A,B,C)− − I⁡ ⁡ ()Y;A,B)≥ ≥ I⁡ ⁡ ()Y;A,C)− − I⁡ ⁡ ()Y;A){displaystyle operatorname {I} (Y;A,B,C)-operatorname {I} (Y;A,B)geq operatorname {I} (Y;A,C)-operatorname {I} (Y;A)}.

Relación con la entropía condicional y conjunta

La información mutua se puede expresar de manera equivalente como:

I⁡ ⁡ ()X;Y)↑ ↑ H()X)− − H()X▪ ▪ Y)↑ ↑ H()Y)− − H()Y▪ ▪ X)↑ ↑ H()X)+H()Y)− − H()X,Y)↑ ↑ H()X,Y)− − H()X▪ ▪ Y)− − H()Y▪ ▪ X){displaystyle {begin{aligned}operatorname {I} (X;Y) {H} (X)-mathrm {H} (Xmid Y)\cH}equiv mathrm {H} (Y)-mathrm {H} (Ymid X)\fnMicrosoft Sans Serif}equiv mathrm {H} (X)+mathrm {H} (Y)-mathrm {H} (X,Y)\ quedarse {}equiv mathrm {H} (X,Y)-mathrm {H} (Xmid Y)-mathrm {H} (Ymid X)end{aligned}}}}}}}

Donde H()X){displaystyle mathrm {H} (X)} y H()Y){displaystyle mathrm {H} (Y)} son los entropies marginales, H()X▪ ▪ Y){displaystyle mathrm {H} (Xmid Y)} y H()Y▪ ▪ X){displaystyle mathrm {H} (Ymid X)} son las entropias condicionales, y H()X,Y){displaystyle mathrm {H} (X,Y)} es la entropía conjunta de X{displaystyle X} y Y{displaystyle Sí..

Observe la analogía con la unión, diferencia e intersección de dos conjuntos: a este respecto, todas las fórmulas dadas anteriormente son evidentes en el diagrama de Venn informado al principio del artículo.

En términos de un canal de comunicación en el que la salida Y{displaystyle Sí. es una versión ruidosa de la entrada X{displaystyle X}, estas relaciones se resumen en la figura:

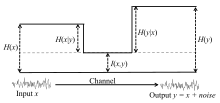
Porque... I⁡ ⁡ ()X;Y){displaystyle operatorname {I} (X;Y)} no negativo, en consecuencia, H()X)≥ ≥ H()X▪ ▪ Y){displaystyle mathrm {H} (X)geq mathrm {H} (Xmid Y)}. Aquí damos la deducción detallada de I⁡ ⁡ ()X;Y)=H()Y)− − H()Y▪ ▪ X){displaystyle operatorname {I} (X;Y)=mathrm {H} (Y)-mathrm {H} (Ymid X)} para el caso de variables aleatorias discretas:

I⁡ ⁡ ()X;Y)=.. x▪ ▪ X,Sí.▪ ▪ Yp()X,Y)()x,Sí.)log⁡ ⁡ p()X,Y)()x,Sí.)pX()x)pY()Sí.)=.. x▪ ▪ X,Sí.▪ ▪ Yp()X,Y)()x,Sí.)log⁡ ⁡ p()X,Y)()x,Sí.)pX()x)− − .. x▪ ▪ X,Sí.▪ ▪ Yp()X,Y)()x,Sí.)log⁡ ⁡ pY()Sí.)=.. x▪ ▪ X,Sí.▪ ▪ YpX()x)pY▪ ▪ X=x()Sí.)log⁡ ⁡ pY▪ ▪ X=x()Sí.)− − .. x▪ ▪ X,Sí.▪ ▪ Yp()X,Y)()x,Sí.)log⁡ ⁡ pY()Sí.)=.. x▪ ▪ XpX()x)().. Sí.▪ ▪ YpY▪ ▪ X=x()Sí.)log⁡ ⁡ pY▪ ▪ X=x()Sí.))− − .. Sí.▪ ▪ Y().. x▪ ▪ Xp()X,Y)()x,Sí.))log⁡ ⁡ pY()Sí.)=− − .. x▪ ▪ XpX()x)H()Y▪ ▪ X=x)− − .. Sí.▪ ▪ YpY()Sí.)log⁡ ⁡ pY()Sí.)=− − H()Y▪ ▪ X)+H()Y)=H()Y)− − H()Y▪ ▪ X).{displaystyle {begin{aligned}operatorname [I] (X;Y) {X}},yin {mathcal {Y}}p_{(X,Y)}(x,y)log {frac {frac {(X,Y)}(x,y)}{p_{X}(x)p_{Y}(y)}\\ {c}=sum _{xin {cH00}in {fn0} {X}},yin {mathcal {Y}}p_{(X,Y)}(x,y)log {frac {frac {p_{(X,Y)}(x,y)}{p_{X}(x)}}-sum _{xin {in {mathcal} {X}},yin {mathcal {Y}}p_{(X,Y)}(x,y)log ¿Por qué? {X},yin {cHFF} {Y}}p_{X}(x)p_{Ymid X=x}(y)log p_{Ymid X=x}(y)-sum _{xin {mathcal] {X}},yin {mathcal {Y}}p_{(X,Y)}(x,y)log ¿Por qué? {X}}p_{X}(x)left(sum _{yin {mathcal) {Y}}p_{Ymid X=x}(y)log p_{Ymid X=x}(y)right)-sum _{yin {mathcal {Y}}}left(sum _{xin {mathcal {X}}p_{(X,Y)}(x,y)right)log p_{Y}(y)\\cH00}=-sum _{xin {mathcal] {X}}p_{X}(x)mathrm {H} (Ymid X=x)-sum _{yin {mathcal {Y}}p_{Y}(y)log p_{Y}(y)\\cH00}=-mathrm {H} (Ymid X)+mathrm {H} (Y)\\fnMicrom {H} (Y)-mathrm {H} (Ymid X).\end{aligned}}}}

Las pruebas de las otras identidades anteriores son similares. La prueba del caso general (no sólo discreto) es similar, con integrales reemplazando a las sumas.

Intuitivamente, si entropía H()Y){displaystyle mathrm {H} (Y)} es considerado como una medida de incertidumbre sobre una variable aleatoria, entonces H()Y▪ ▪ X){displaystyle mathrm {H} (Ymid X)} es una medida de lo que X{displaystyle X} ¿Sí? no dicen: Y{displaystyle Sí.. Esta es "la cantidad de incertidumbre que queda sobre Y{displaystyle Sí. después X{displaystyle X} es conocido", y por lo tanto el lado derecho de la segunda de estas igualdades se puede leer como "la cantidad de incertidumbre en Y{displaystyle Sí., menos la cantidad de incertidumbre en Y{displaystyle Sí. que queda después X{displaystyle X} es conocido", que equivale a "la cantidad de incertidumbre en Y{displaystyle Sí. que se elimina por saber X{displaystyle X}". Esto corrobora el significado intuitivo de la información mutua como la cantidad de información (es decir, la reducción de la incertidumbre) que saber o variable proporciona sobre la otra.

Note que en el caso discreto H()Y▪ ▪ Y)=0{displaystyle mathrm {H} (Ymid Y)=0} por lo tanto H()Y)=I⁡ ⁡ ()Y;Y){displaystyle mathrm [H} (Y)=operatorname {I} (Y;Y)}. Así I⁡ ⁡ ()Y;Y)≥ ≥ I⁡ ⁡ ()X;Y){displaystyle operatorname {I} (Y;Y)geq operatorname {I} (X;Y)}, y uno puede formular el principio básico que una variable contiene al menos tanta información sobre sí mismo como cualquier otra variable puede proporcionar.

Relación con la divergencia Kullback-Leibler

Para parejas mixtas discretas o continuas ()X,Y){displaystyle (X,Y)}, información mutua es la divergencia Kullback-Leibler del producto de las distribuciones marginales, pX⋅ ⋅ pY{displaystyle P_{X}cdot P_{Y}, de la distribución conjunta p()X,Y){displaystyle p_{(X,Y)}, es decir,

Además, dejemos p()X,Y)()x,Sí.)=pX▪ ▪ Y=Sí.()x)Alternativa Alternativa pY()Sí.){displaystyle p_{(X,Y)}(x,y)=p_{Xmid Y=y}(x)*p_{Y}(y)} sea la función de masa condicional o densidad. Entonces, tenemos la identidad

La prueba para variables aleatorias discretas conjuntas es la siguiente:

I⁡ ⁡ ()X;Y)=.. Sí.▪ ▪ Y.. x▪ ▪ Xp()X,Y)()x,Sí.)log⁡ ⁡ ()p()X,Y)()x,Sí.)pX()x)pY()Sí.))=.. Sí.▪ ▪ Y.. x▪ ▪ XpX▪ ▪ Y=Sí.()x)pY()Sí.)log⁡ ⁡ pX▪ ▪ Y=Sí.()x)pY()Sí.)pX()x)pY()Sí.)=.. Sí.▪ ▪ YpY()Sí.).. x▪ ▪ XpX▪ ▪ Y=Sí.()x)log⁡ ⁡ pX▪ ▪ Y=Sí.()x)pX()x)=.. Sí.▪ ▪ YpY()Sí.)DKL()pX▪ ▪ Y=Sí.∥ ∥ pX)=EY[DKL()pX▪ ▪ Y∥ ∥ pX)].{displaystyle {begin{aligned}operatorname [I] (X;Y) {Y}}}sum _{xin {mathcal {X}}{p_{(X,Y)}(x,y)log left({frac {p_{(X,Y)}(x,y)}{p_{X}(x),p_{Y}(y)}}right)}du)}du)}s_} {y)} {y)} {y)} {s} {s} {s} {s} {s} {s} {s} {s} {s}s}s}s}s}s}s}s}s}s}s}s}s} {s}s}s}s}s}s}s} {s}s}s}s}s}s}s}s}s}s}s}s}s}s}s}s}s {Y}}sum _{xin {cHFF} {cHFF}}}sum _{xin {fn}in {fn} {fn} {fn}fn}fn}fnfnfnfnfnfnfnfnh}fnfnfnfnh}fnh}fnfnfnfnfnfnh}fnfnfnfnfnfnh}fnfnfnfnfnfnfnfnh}fnfnfnfnfnh}fnhnh}fnhnh}fnhnfnfnh}fnh}fnh}fnfnh}fncHFF}cHFF}cfnh}c {X}p_{Xmid Y=y}(x)p_{Y}(y)log {frac {p_{Xmid Y=y}(x)p_{Y}(y)}{p_{X}(x)p_{Y}(y)}}\\\cH00=sum ¿Por qué? Sí. {X}}p_{Xmid Y=y}(x)log {frac {p_{Xmid Y=y}(x)} {p_{X}}\\\cH00=sum _{yin {mathcal {Y}}p_{Y}(y);D_{text{KL}!left(p_{Xmidmid Y=y'parallel P_{X}derecha)\\cH003 {fnMicrosoft Sans}fnMicrosoft Sans Serif} Y'parallel Bien.

De manera similar, esta identidad se puede establecer para variables aleatorias continuas conjuntas.

Tenga en cuenta que aquí la divergencia Kullback-Leibler implica la integración sobre los valores de la variable aleatoria X{displaystyle X} sólo, y la expresión DKL()pX▪ ▪ Y∥ ∥ pX){displaystyle D_{text{KL}(p_{Xmid Y}parallel P_{X}} todavía denota una variable al azar porque Y{displaystyle Sí. es al azar. Así la información mutua también puede entenderse como la expectativa de la divergencia Kullback-Leibler de la distribución univariada pX{displaystyle P_{X} de X{displaystyle X} de la distribución condicional pX▪ ▪ Y{displaystyle p_{Xmid Sí. de X{displaystyle X} dado Y{displaystyle Sí.: las distribuciones más diferentes pX▪ ▪ Y{displaystyle p_{Xmid Sí. y pX{displaystyle P_{X} son en promedio, cuanto mayor es el aumento de la información.

Estimación bayesiana de información mutua

Si se dispone de muestras de una distribución conjunta, se puede utilizar un enfoque bayesiano para estimar la información mutua de esa distribución. El primer trabajo para hacer esto, que también mostró cómo hacer la estimación bayesiana de muchas otras propiedades teóricas de información además de la información mutua, fue. Los investigadores posteriores han redireccionado y extendido este análisis. Véase para un documento reciente basado en un anterior específicamente adaptado a la estimación de mutuo información per se. Además, recientemente un método de estimación contable para productos continuos y multivariables, Y{displaystyle Sí., se propuso en .

Supuestos de independencia

La formulación de divergencias Kullback-Leibler de la información mutua se basa en que uno está interesado en comparar p()x,Sí.){displaystyle p(x,y)} al producto exterior plenamente factorizado p()x)⋅ ⋅ p()Sí.){displaystyle p(x)cdot p(y)}. En muchos problemas, como la factorización de matriz no negativa, uno está interesado en las factorizaciones menos extremas; específicamente, uno desea comparar. p()x,Sí.){displaystyle p(x,y)} a una aproximación de matriz de bajo rango en alguna variable desconocida w{displaystyle w}; es decir, en qué grado uno podría tener

p()x,Sí.).. .. wp.. ()x,w)p.. .. ()w,Sí.){displaystyle p(x,y)approx sum _{w}p^{prime }(x,w)p^{primeprime }(w,y)}

Alternately, one might be interested in learning how much more information p()x,Sí.){displaystyle p(x,y)} lleva a cabo su factorización. En tal caso, el exceso de información que la distribución completa p()x,Sí.){displaystyle p(x,y)} la factorización de la matriz es dada por la divergencia Kullback-Leibler

ILRMA=.. Sí.▪ ▪ Y.. x▪ ▪ Xp()x,Sí.)log⁡ ⁡ ()p()x,Sí.).. wp.. ()x,w)p.. .. ()w,Sí.)),{displaystyle operatorname [I] _{LRMA}=sum _{yin {mathcal {Y}}}sum _{xin {mathcal {X}}{p(x,y)log {left({frac {p(x,y)}{sum _{w}p^{prime }(x,w)p^{primeprimeprime }(w,y)}}right)}}}}}}}} {}}}}}} {}}} {}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}} {}}}}} {s}}}}}}}}}} {s}}}}}}}}}}}}}}}}} {s}}} {s}}}}}}}}}}}}}}}} {}}}}}}}}s}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} }

La definición convencional de la información mutua se recupera en el caso extremo de que el proceso W{displaystyle W. tiene sólo un valor w{displaystyle w}.

Variaciones

Se han propuesto varias variaciones de la información mutua para satisfacer diversas necesidades. Entre ellas se encuentran variantes normalizadas y generalizaciones a más de dos variables.

Métrica

Muchas aplicaciones requieren una métrica, es decir, una medida de distancia entre pares de puntos. La cantidad

d()X,Y)=H()X,Y)− − I⁡ ⁡ ()X;Y)=H()X)+H()Y)− − 2I⁡ ⁡ ()X;Y)=H()X▪ ▪ Y)+H()Y▪ ▪ X)=2H()X,Y)− − H()X)− − H()Y){displaystyle {begin{aligned}d(X,Y) implica=mathrm {H} (X,Y)-operatorname {I} (X;Y)\\ simultáneamente=mathrm {H} (X)+mathrm {H} (Y)-2operatorname {I} (X;Y)\\cH=mathrm} {H} (Xmid Y)+mathrm {H} (Ymid X)\\2mathrm {H} (X, Y)-mathrm {H} (X)-mathrm {H} (Y)end{aligned}}}

satisfies the properties of a metric (triangle inequality, non-negativity, indiscernibility and symmetry). This distance metric is also known as the variation of information.

Si X,Y{displaystyle X,Y} son variables discretas al azar entonces todos los términos entropía no son negativos, por lo que 0≤ ≤ d()X,Y)≤ ≤ H()X,Y){displaystyle 0leq d(X,Y)leq mathrm {H} (X,Y)} y uno puede definir una distancia normalizada

D()X,Y)=d()X,Y)H()X,Y)≤ ≤ 1.{displaystyle D(X,Y)={frac {d(X,Y)}{mathrm {H} (X,Y)}}leq 1.}

La métrica D{displaystyle D} es una métrica universal, en que si alguna otra medida de distancia X{displaystyle X} y Y{displaystyle Sí. cerca, entonces el D{displaystyle D} también los juzgará cerca.

Introducir las definiciones muestra que

D()X,Y)=1− − I⁡ ⁡ ()X;Y)H()X,Y).{displaystyle D(X,Y)=1-{frac {fnMicrosoft Sans Serif}{mathrm {H}}}}

Esto se conoce como la Distancia Rajski. En una interpretación teorética de la información (ver la figura para la entropía condicional), esta es efectivamente la distancia de Jaccard entre X{displaystyle X} y Y{displaystyle Sí..

Finalmente,

D.. ()X,Y)=1− − I⁡ ⁡ ()X;Y)max{}H()X),H()Y)}{displaystyle D^{prime }(X,Y)=1-{frac {operatorname {I} (X;Y)}{max left{mathrm {H} (X),mathrm {H} (Y)right}}}}

también es una métrica.

Información mutua condicional

A veces es útil expresar la información mutua de dos variables aleatorias condicionadas a una tercera.

Para variables aleatorias discretas conjuntas, esto toma la forma

I⁡ ⁡ ()X;YSilencioZ)=.. z▪ ▪ Z.. Sí.▪ ▪ Y.. x▪ ▪ XpZ()z)pX,YSilencioZ()x,Sí.Silencioz)log⁡ ⁡ [pX,YSilencioZ()x,Sí.Silencioz)pXSilencioZ()xSilencioz)pYSilencioZ()Sí.Silencioz)],{displaystyle operatorname {I} (X;Y privacyZ)=sum _{zin {mathcal {Z}sum _{yin {mathcal] {Y}}}sum _{xin {mathcal {X}}{p_{Z}(z),p_{X,Y sometidaZ}(x,y sometidaz)log left[{frac {p_{X,Y:i)}{p_{X}x}x}f}fnMis)}p} {f} {f} {f}}}f}}}}}}}}}}f}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}}f}f}f}f}f}f}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}

que se puede simplificar como

I⁡ ⁡ ()X;YSilencioZ)=.. z▪ ▪ Z.. Sí.▪ ▪ Y.. x▪ ▪ XpX,Y,Z()x,Sí.,z)log⁡ ⁡ pX,Y,Z()x,Sí.,z)pZ()z)pX,Z()x,z)pY,Z()Sí.,z).{displaystyle operatorname {I} (X;Y privacyZ)=sum _{zin {mathcal {Z}sum _{yin {mathcal] {Y}}}sum _{xin {mathcal {X}}p_{X,Y,Z}(x,y,z)log {frac {frac {_{X,Y,Z}(x,y,z)p_{Z}(z)}{p_{X,Z}(x,z)p_{Y,Z} {y,z)}}}}}}}} {}}}}}} {s}} {s}}}}}} {s} {s}}}}}}} {s}}}} {s}}} {s}} {s}}}}}}} {s}}}}}}}} {s} {s} {s}} {s}}}} {s}}}} {s_s_}}}}}}}}}}}}}}}} {s}}}}}}}}}}}}}}}} {s}}} {

Para variables aleatorias continuas conjuntas, esto toma la forma

I⁡ ⁡ ()X;YSilencioZ)=∫ ∫ Z∫ ∫ Y∫ ∫ XpZ()z)pX,YSilencioZ()x,Sí.Silencioz)log⁡ ⁡ [pX,YSilencioZ()x,Sí.Silencioz)pXSilencioZ()xSilencioz)pYSilencioZ()Sí.Silencioz)]dxdSí.dz,{displaystyle operatorname {I} (X;Y sometidaZ)=int _{mathcal ################################################################################################################################################################################################################################################################ {Y}}int _{mathcal {X}{p_{Z}(z),p_{X,Y sometidaZ}(x,y sometidaz)log left[{frac {p_{X,Y perpetuaZ}(x,y eternaz)}{p_{X:i}d}} {y}d}}

que se puede simplificar como

I⁡ ⁡ ()X;YSilencioZ)=∫ ∫ Z∫ ∫ Y∫ ∫ XpX,Y,Z()x,Sí.,z)log⁡ ⁡ pX,Y,Z()x,Sí.,z)pZ()z)pX,Z()x,z)pY,Z()Sí.,z)dxdSí.dz.{displaystyle operatorname {I} (X;Y sometidaZ)=int _{mathcal ################################################################################################################################################################################################################################################################ {Y}}int _{mathcal {X}p_{X,Y,Z}(x,y,z)log {frac {frac {p_{X,Y,Z}(x,y,z)p_{Z} {p_{X,Z}(x,z)p_{Y,Z}(y,z)}dxdydz}}

El condicionamiento sobre una tercera variable aleatoria puede aumentar o disminuir la información mutua, pero siempre es cierto que

I⁡ ⁡ ()X;YSilencioZ)≥ ≥ 0{displaystyle operatorname {I} (X;Y resistZ)geq 0}

para variables discretas y distribuidas conjuntamente X,Y,Z{displaystyle X,Y,Z}. Este resultado se ha utilizado como un edificio básico para probar otras desigualdades en la teoría de la información.

Información de interacción

Se han propuesto varias generalizaciones de información mutua a más de dos variables aleatorias, como la correlación total (o información múltiple) y la correlación total dual. La expresión y el estudio de información mutua multivariada de alto grado se logró en dos trabajos aparentemente independientes: McGill (1954), que denominó a estas funciones "información de interacción", y Hu Kuo Ting (1962). La información de interacción se define para una variable de la siguiente manera:

I⁡ ⁡ ()X1)=H()X1){displaystyle operatorname {I} (X_{1}=mathrm {H} (X_{1})}

y para 1,}" xmlns="http://www.w3.org/1998/Math/MathML">n■1,{displaystyle n título1,}1," aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/957e317312fd02f34c1d1c8c80bd8484c29fde6c" style="vertical-align: -0.671ex; width:6.302ex; height:2.509ex;"/>

I⁡ ⁡ ()X1;...;Xn)=I⁡ ⁡ ()X1;...;Xn− − 1)− − I⁡ ⁡ ()X1;...;Xn− − 1▪ ▪ Xn).{displaystyle operatorname {I} (X_{1};,,;X_{n}=operatorname [I} (X_{1};,,;X_{n-1})-operatorname {I} (X_{1};,...,X_{n-1}mid X_{n}

Algunos autores invierten el orden de los términos del lado derecho de la ecuación anterior, lo que cambia el signo cuando el número de variables aleatorias es impar. (Y en este caso, la expresión de una sola variable se convierte en el negativo de la entropía). Tenga en cuenta que

I()X1;...... ;Xn− − 1▪ ▪ Xn)=EXn[DKL()P()X1,...... ,Xn− − 1)▪ ▪ Xn.. PX1▪ ▪ Xn⊗ ⊗ ⋯ ⋯ ⊗ ⊗ PXn− − 1▪ ▪ Xn)].{displaystyle I(X_{1};ldots;X_{n-1}mid X_{n}=mathbb [E] _{X_{n} [D_{mathrm {KL}(P_{(X_{1},ldotsX_{n-1})mid X_{n}fn_{X_{1}mid X_{n}otimes cdots otimes P_{X_{n-1}mid X_{n})].}

Independencia estadística multivariante

Las funciones de información mutua multivariada generalizan el caso de independencia de pareja que afirma que X1,X2{displaystyle X_{1},X_{2} si I()X1;X2)=0{displaystyle I(X_{1};X_{2}=0}, a numerosas variables arbitrarias. n variables son mutuamente independientes si y sólo si 2n− − n− − 1{displaystyle 2^{n}-n-1} Desaparecieron las funciones de información mutua I()X1;...... ;Xk)=0{displaystyle I(X_{1};ldots;X_{k}=0} con n≥ ≥ k≥ ≥ 2{displaystyle ngeq kgeq 2} (teorema 2). En este sentido, el I()X1;...... ;Xk)=0{displaystyle I(X_{1};ldots;X_{k}=0} se puede utilizar como un refinado criterio de independencia estadística.

Aplicaciones

Para 3 variables, Brenner et al. aplicó información mutua multivariada a la codificación neuronal y llamó a su negatividad "sinergia" y Watkinson et al. lo aplicó a la expresión genética. Para k variables arbitrarias, Tapia et al. información mutua multivariada aplicada a la expresión genética. Puede ser cero, positivo o negativo. La positividad corresponde a relaciones que generalizan las correlaciones por pares, la nulidad corresponde a una noción refinada de independencia y la negatividad detecta relaciones "emergentes" de alta dimensión. relaciones y puntos de datos agrupados).

Un esquema de generalización de alta dimensión que maximiza la información mutua entre la distribución conjunta y otras variables objetivo resulta útil en la selección de características.

La información mutua también se utiliza en el área del procesamiento de señales como medida de similitud entre dos señales. Por ejemplo, la métrica FMI es una medida del rendimiento de la fusión de imágenes que utiliza información mutua para medir la cantidad de información que contiene la imagen fusionada sobre las imágenes de origen. El código Matlab para esta métrica se puede encontrar en. Está disponible un paquete de Python para calcular toda la información mutua multivariante, información mutua condicional, entropías conjuntas, correlaciones totales y distancia de información en un conjunto de datos de n variables.

Información dirigida

Información dirigida, I⁡ ⁡ ()Xn→ → Yn){displaystyle operatorname {I} left(X^{n}to Y^{n}right)}, mide la cantidad de información que fluye del proceso Xn{displaystyle X^{n} a Yn{displaystyle Y., donde Xn{displaystyle X^{n} denota el vector X1,X2,...,Xn{displaystyle X_{1},X_{2}, X_{n} y Yn{displaystyle Y. denotaciones Y1,Y2,...,Yn{displaystyle Y.... El término información dirigida fue acuñado por James Massey y se define como

I⁡ ⁡ ()Xn→ → Yn)=.. i=1nI⁡ ⁡ ()Xi;Yi▪ ▪ Yi− − 1){displaystyle operatorname {I} left(X^{n}to Y^{n}right)=sum ################################################################################################################################################################################################################################################################ {I} left(X_{i};Y_{i}mid Sí..

Note que si n=1{displaystyle n=1}, la información dirigida se convierte en la información mutua. La información dirigida tiene muchas aplicaciones en problemas donde la causalidad desempeña un papel importante, como la capacidad de canal con retroalimentación.

Variantes normalizadas

Las variantes normalizadas de la información mutua son proporcionadas por los coeficientes de restricción, coeficiente de incertidumbre o competencia:

CXY=I⁡ ⁡ ()X;Y)H()Y)yCYX=I⁡ ⁡ ()X;Y)H()X).{displaystyle ¿Qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}

Los dos coeficientes tienen un valor comprendido entre [0, 1], pero no son necesariamente iguales. En algunos casos puede ser deseable una medida simétrica, como la siguiente medida de redundancia:

R=I⁡ ⁡ ()X;Y)H()X)+H()Y){displaystyle ¿Qué?

que alcanza un mínimo de cero cuando las variables son independientes y un valor máximo de

Rmax=min{}H()X),H()Y)}H()X)+H()Y){displaystyle R_{max }={frac {min left{mathrm {H} (X),mathrm {H} {Y)}{mathrm {H} (X)+mathrm {H}}}}}

cuando una variable se vuelve completamente redundante con el conocimiento de la otra. Véase también Redundancia (teoría de la información).

Otra medida simétrica es la incertidumbre simétrica (Witten & Frank 2005), dada por

U()X,Y)=2R=2I⁡ ⁡ ()X;Y)H()X)+H()Y){displaystyle U(X,Y)=2R=2{frac {operatorname {I} (X;Y)}{mathrm {H} (X)+mathrm {H}}}}}

que representa la media armónica de los dos coeficientes de incertidumbre CXY,CYX{displaystyle C_{XY},C_{YX}.

Si consideramos la información mutua como un caso especial de correlación total o correlación total dual, las versiones normalizadas son, respectivamente,

I⁡ ⁡ ()X;Y)min[H()X),H()Y)]{displaystyle {frac {fnMicroc} {I} (X;Y)}{min left [mathrm {H} (X),mathrm {H} (Y)right]}}} y I⁡ ⁡ ()X;Y)H()X,Y).{displaystyle {frac {fnMicroc} {I} (X;Y)} {mathrm {H}};.}

Esta versión normalizada también conocida como Ratio de Calidad de la Información (IQR) que cuantifica la cantidad de información de una variable en función de otra variable frente a una incertidumbre total:

IQR()X,Y)=E⁡ ⁡ [I⁡ ⁡ ()X;Y)]=I⁡ ⁡ ()X;Y)H()X,Y)=.. x▪ ▪ X.. Sí.▪ ▪ Yp()x,Sí.)log⁡ ⁡ p()x)p()Sí.).. x▪ ▪ X.. Sí.▪ ▪ Yp()x,Sí.)log⁡ ⁡ p()x,Sí.)− − 1{displaystyle IQR(X,Y)=operatorname [operatorname {I} (X;Y)]={frac {operatorname {I} (X;Y)}{mathrm {H}}={frac {sum _{xin) X}sum _{yin Y}p(x,y)log {p(x)p(y)}{sum _{xin X}sum _{yin Sí.

Existe una normalización que se deriva de pensar primero en la información mutua como análoga a la covarianza (por lo tanto, la entropía de Shannon es análoga a la varianza). Luego, la información mutua normalizada se calcula de manera similar al coeficiente de correlación de Pearson,

I⁡ ⁡ ()X;Y)H()X)H()Y).{displaystyle {frac {fnMicroc} {I} (X;Y)}{sqrt {mathrm {H} (X)mathrm {H}}};.}

Variantes ponderadas

En la formulación tradicional de la información mutua,

I⁡ ⁡ ()X;Y)=.. Sí.▪ ▪ Y.. x▪ ▪ Xp()x,Sí.)log⁡ ⁡ p()x,Sí.)p()x)p()Sí.),{displaystyle operatorname {I} (X;Y)=sum _{yin Y}sum _{xin X}p(x,y)log {frac {p(x,y)}{p(x),p(y)}}}}

cada uno evento o objeto especificado ()x,Sí.){displaystyle (x,y)} es ponderado por la probabilidad correspondiente p()x,Sí.){displaystyle p(x,y)}. Esto supone que todos los objetos o eventos son equivalentes aparte de su probabilidad de ocurrencia. Sin embargo, en algunas aplicaciones puede ser el caso de que ciertos objetos o eventos sean más significativa que otros, o que ciertos patrones de asociación son más semánticamente importantes que otros.

Por ejemplo, la cartografía determinista {}()1,1),()2,2),()3,3)}{displaystyle {(1,1),(2,2),(3,3)} puede ser visto como más fuerte que la cartografía determinista {}()1,3),()2,1),()3,2)}{displaystyle {(1,3),(2,1),(3,2)}, aunque estas relaciones producirían la misma información mutua. Esto se debe a que la información mutua no es sensible en absoluto a cualquier orden inherente en los valores variables (Cronbach 1954, Coombs, Dawes & Tversky 1970, Lockhead 1970), y por lo tanto no es sensible en absoluto al forma de la cartografía relacional entre las variables asociadas. Si se desea que la relación anterior —que muestra acuerdo sobre todos los valores variables— se juzgue más fuerte que la relación posterior, entonces es posible utilizar lo siguiente ponderada información mutua (Guiasu 1977).

I⁡ ⁡ ()X;Y)=.. Sí.▪ ▪ Y.. x▪ ▪ Xw()x,Sí.)p()x,Sí.)log⁡ ⁡ p()x,Sí.)p()x)p()Sí.),{displaystyle operatorname {I} (X;Y)=sum _{yin Y}sum _{xin X}w(x,y)p(x,y)log {frac {p(x,y)}{p(x),p(y)}}}}}}

que coloca un peso w()x,Sí.){displaystyle w(x,y)} sobre la probabilidad de cada co-ocurrencia de valor variable, p()x,Sí.){displaystyle p(x,y)}. Esto permite que ciertas probabilidades puedan tener más o menos importancia que otras, permitiendo así la cuantificación de la relevancia holístico o Prägnanz factores. En el ejemplo anterior, utilizando pesos relativos más grandes para w()1,1){displaystyle w(1,1)}, w()2,2){displaystyle w(2,2)}, y w()3,3){displaystyle w(3,3)} tendría el efecto de evaluar mayor información para la relación {}()1,1),()2,2),()3,3)}{displaystyle {(1,1),(2,2),(3,3)} que para la relación {}()1,3),()2,1),()3,2)}{displaystyle {(1,3),(2,1),(3,2)}, que puede ser deseable en algunos casos de reconocimiento de patrones, y similares. Esta información mutua ponderada es una forma de KL-Divergence ponderada, que se sabe que toma valores negativos para algunos insumos, y hay ejemplos donde la información mutua ponderada también toma valores negativos.

Información mutua ajustada

Una distribución de probabilidad puede verse como una partición de un conjunto. Cabe entonces preguntarse: si un conjunto se dividiera aleatoriamente, ¿cuál sería la distribución de probabilidades? ¿Cuál sería el valor esperado de la información mutua? La información mutua ajustada o AMI resta el valor esperado del IM, de modo que el AMI es cero cuando dos distribuciones diferentes son aleatorias y uno cuando dos distribuciones son idénticas. El AMI se define de forma análoga al índice Rand ajustado de dos particiones diferentes de un conjunto.

Información mutua absoluta

Utilizando las ideas de complejidad de Kolmogorov, se puede considerar la información mutua de dos secuencias independientes de cualquier distribución de probabilidad:

IK⁡ ⁡ ()X;Y)=K()X)− − K()X▪ ▪ Y).{displaystyle operatorname [I} _{K}(X;Y)=K(X)-K(Xmid Y).}

Para establecer que esta cantidad es simétrica hasta un factor logarítmico (IK⁡ ⁡ ()X;Y).. IK⁡ ⁡ ()Y;X){displaystyle operatorname {I} _{K}(X;Y)approx operatorname {I} _{K}(Y;X)}) se requiere la regla de cadena para la complejidad de Kolmogorov (Li & Vitányi 1997). Las aproximaciones de esta cantidad a través de la compresión se pueden utilizar para definir una medida de distancia para realizar un agrupamiento jerárquico de secuencias sin tener ningún conocimiento de dominio de las secuencias (Cilibrasi & Vitányi 2005).

Correlación lineal

A diferencia de los coeficientes de correlación, como el coeficiente de correlación del momento del producto, la información mutua contiene información sobre toda dependencia, lineal y no lineal, y no sólo la dependencia lineal como las medidas de coeficiente de correlación. Sin embargo, en el caso estrecho de que la distribución conjunta X{displaystyle X} y Y{displaystyle Sí. es una distribución normal bivariada (en particular, que ambas distribuciones marginales se distribuyen normalmente), hay una relación exacta entre I{displaystyle operatorname {I} y el coeficiente de correlación *** *** {displaystyle rho } (Gel'fand & Yaglom 1957).

I=− − 12log⁡ ⁡ ()1− − *** *** 2){displaystyle operatorname {I} =-{frac {1}{2}log left(1-rho ^{2}right)}

La ecuación anterior se puede derivar de la siguiente manera para un gaussiano bivariado:

()X1X2)♪ ♪ N()()μ μ 1μ μ 2),.. ),.. =()σ σ 12*** *** σ σ 1σ σ 2*** *** σ σ 1σ σ 2σ σ 22)H()Xi)=12log⁡ ⁡ ()2π π eσ σ i2)=12+12log⁡ ⁡ ()2π π )+log⁡ ⁡ ()σ σ i),i▪ ▪ {}1,2}H()X1,X2)=12log⁡ ⁡ [()2π π e)2Silencio.. Silencio]=1+log⁡ ⁡ ()2π π )+log⁡ ⁡ ()σ σ 1σ σ 2)+12log⁡ ⁡ ()1− − *** *** 2){beplaystyle {begin{aligned}{begin{pmatrix}X_{1}X_{2}end{pmatrix} {sim {mathcal {N}left({begin{pmatrix}mutrix} _{1}\\mu _{2}end{pmatrix}}Sigma right),qquad Sigma ={begin{pmatrix}sigma ################################################################################################################################################################################################################################################################ _{2}\\\rho sigma _{1}sigma - ¿Qué? ################################################################################################################################################################################################################################################################ {H} (X_{i}) {2}{2}}log(2pi)+log left(sigma _{i}just),quad iin {1,2}mathrm {H} (X_{1},X_{2}) {={frac {1}{2}log left[(2pi e)^{2}Sigma ¦right]=1+log(2pi)+log left(sigma _{1}sigma _{2}right)+{2}{2}{2}{} {1} {}{}{}}}}}{}{}}{}{2}{}}{}}}}}}}}}}}{}{}}}}}}{}{}}}}}}}} {}}} {}}}}}}}}}}}}}} {}}}}}} {}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Por lo tanto,

I⁡ ⁡ ()X1;X2)=H()X1)+H()X2)− − H()X1,X2)=− − 12log⁡ ⁡ ()1− − *** *** 2){displaystyle operatorname {I} left(X_{1};X_{2}right)=mathrm {H} left(X_{1}right)+mathrm {H}left(X_{2}right)-mathrm {H}left(X_{1}right)=-{2}{2}{2}{2}{2} {}{}} {}}}}}}}{2}}}}}}}}}}}}{}{2}}}}}}}}}}}} {}} {}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Para datos discretos

Cuando X{displaystyle X} y Y{displaystyle Sí. se limitan a estar en un número discreto de estados, los datos de observación se resumen en una tabla de contingencia, con variable de fila X{displaystyle X} (o i{displaystyle i}) y variable columna Y{displaystyle Sí. (o j{displaystyle j}). La información mutua es una de las medidas de asociación o correlación entre las variables de fila y columna.

Otras medidas de asociación incluyen las estadísticas de prueba de Pearson, estadísticas de pruebas G, etc. De hecho, con la misma base logística, la información mutua será igual a la estadística de probabilidad log-test G dividida por 2N{displaystyle 2N}, donde N{displaystyle N} es el tamaño de la muestra.

Aplicaciones

En muchas aplicaciones, se desea maximizar la información mutua (aumentando así las dependencias), lo que a menudo equivale a minimizar la entropía condicional. Ejemplos incluyen:

• En la tecnología del motor de búsqueda, la información mutua entre frases y contextos se utiliza como una característica para agrupar los medios k para descubrir los cúmulos semánticos (conceptos). Por ejemplo, la información mutua de un bigram podría calcularse como:

Donde fXY{displaystyle F_{XY} es el número de veces que el bigram xy aparece en el cuerpo, fX{displaystyle F_{X} es el número de veces que el unigram x aparece en el corpus, B es el número total de bigrams, y U es el número total de unigrams.

• En las telecomunicaciones, la capacidad del canal es igual a la información mutua, maximizada sobre todas las distribuciones de insumos.
• Se han propuesto procedimientos de formación discriminatoria para los modelos ocultos de Markov basados en el criterio máximo de información mutua (MMI).
• Predicción de la estructura secundaria RNA de una alineación de secuencia múltiple.
• Predicción de perfiles fitogenéticos del presente pareado y desaparición de genes funcionalmente ligados.
• La información mutua se ha utilizado como criterio para la selección de características y las transformaciones de características en el aprendizaje automático. Se puede utilizar para caracterizar tanto la relevancia como la redundancia de variables, como la selección de características de redundancia mínima.
• Se utiliza información mutua para determinar la similitud de dos agrupaciones diferentes de un conjunto de datos. Como tal, proporciona algunas ventajas sobre el índice tradicional Rand.
• La información mutua de las palabras se utiliza a menudo como una función importante para la computación de las collocaciones en el corpus lingüístico. Esto tiene la complejidad agregada de que ninguna palabra-instancia es una instancia a dos palabras diferentes; más bien, se cuenta casos en que 2 palabras ocurren adyacentes o en estrecha proximidad; esto complica ligeramente el cálculo, ya que la probabilidad esperada de una palabra ocurre dentro de N{displaystyle N} palabras de otra, va con N{displaystyle N}
• La información mutua se utiliza en imágenes médicas para el registro de imágenes. Dada una imagen de referencia (por ejemplo, un escaneo cerebral), y una segunda imagen que debe ser puesta en el mismo sistema de coordenadas como la imagen de referencia, esta imagen se deforma hasta que se maximice la información mutua entre ella y la imagen de referencia.
• Detección de sincronización de fases en el análisis de series temporales.
• En el método infomax para el aprendizaje de redes neuronales y otras máquinas, incluyendo el algoritmo de análisis de componentes independiente basado en infomax
• Se utiliza la media de información mutua en el retraso en la incrustación de teorema para determinar el demoras en la financiación Parámetro.
• La información mutua entre los genes en los datos de microarray de expresión es utilizada por el algoritmo ARACNE para la reconstrucción de las redes de genes.
• En la mecánica estadística, la paradoja de Loschmidt puede expresarse en términos de información mutua. Loschmidt señaló que debe ser imposible determinar una ley física que carece de simetría reversal (por ejemplo, la segunda ley de la termodinámica) sólo de leyes físicas que tienen esta simetría. Señaló que el teorema H de Boltzmann hizo la suposición de que las velocidades de las partículas en un gas no estaban permanentemente relacionadas, lo que removió la simetría del tiempo inherente al teorema H. Se puede demostrar que si un sistema es descrito por una densidad de probabilidad en el espacio de fase, el teorema de Liouville implica que la información conjunta (negativa de la entropía conjunta) de la distribución sigue siendo constante en el tiempo. La información conjunta es igual a la información mutua más la suma de toda la información marginal (negativa de las entropías marginales) para cada coordenadas de partículas. La suposición de Boltzmann equivale a ignorar la información mutua en el cálculo de la entropía, que produce la entropía termodinámica (dividida por la constante Boltzmann).
• En procesos estocásticos unidos a entornos cambiantes, se puede utilizar información mutua para desenredar dependencias ambientales internas y eficaces. Esto es particularmente útil cuando un sistema físico experimenta cambios en los parámetros que describen su dinámica, por ejemplo, cambios en la temperatura.
• La información mutua se utiliza para aprender la estructura de redes Bayesianas/redes Bayesianas dinamicas, que se piensa explicar la relación causal entre variables aleatorias, como lo demuestra el conjunto de herramientas GlobalMIT: aprender la red Bayesiana dinámica globalmente óptima con el criterio de Prueba de Información Mutua.
• La información mutua se utiliza para cuantificar la información transmitida durante el procedimiento de actualización en el algoritmo de muestreo de Gibbs.
• Función de coste popular en el aprendizaje de árboles de decisión.
• La información mutua se utiliza en la cosmología para probar la influencia de entornos a gran escala sobre propiedades galaxias en el zoo Galaxy.
• La información mutua se utilizó en Física Solar para derivar el perfil de rotación diferencial solar, un mapa de desviación de tiempo de viaje para manchas solares y un diagrama de distancia de mediciones silenciosas.
• Utilizado en Invariant Information Clustering para capacitar automáticamente clasificadores de red neuronales y segmentadores de imágenes sin datos etiquetados.