Índice jaccard

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Medición de similitud y diversidad entre conjuntos

Intersección y unión de dos conjuntos A y B

Intersección sobre Unión como medida de similitud para la detección de objetos en imágenes - una tarea importante en la visión de la computadora.

El índice de Jaccard, también conocido como coeficiente de similitud de Jaccard, es una estadística utilizada para medir la similitud y diversidad de conjuntos de muestras.

Fue desarrollado por Grove Karl Gilbert en 1884 como su índice de verificación (v) y ahora se lo conoce con frecuencia como el índice de éxito crítico en meteorología. Posteriormente fue desarrollado de forma independiente por Paul Jaccard, dándole originalmente el nombre francés coeficiente de comunidad, y formulado nuevamente de forma independiente por T. Tanimoto. Así, el índice de Tanimoto o el coeficiente de Tanimoto también se utilizan en algunos campos. Sin embargo, son idénticos en general al tomar la proporción de Intersección sobre Unión.

Descripción general

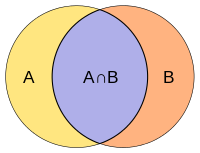
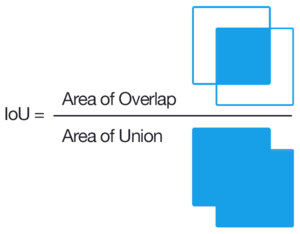
El coeficiente de Jaccard mide la similitud entre conjuntos de muestras finitos y se define como el tamaño de la intersección dividido por el tamaño de la unión de los conjuntos de muestras:

{displaystyle J(A,B)={{|Acap B|} over {|Acup B|}}={{|Acap B|} over {|A|+|B|-|Acap B|}}.}

Note que por diseño, ${displaystyle 0leq J(A,B)leq 1.}$ Si A intersección B está vacío, entonces J()A,B) = 0. El coeficiente de Jaccard es ampliamente utilizado en la ciencia informática, ecología, genómica y otras ciencias, donde se utilizan datos binarios o binarizados. Tanto la solución exacta como los métodos de aproximación están disponibles para pruebas de hipótesis con el coeficiente de Jaccard.

La similitud de Jaccard también se aplica a los bolsos, es decir, a los Multisets. Tiene una fórmula similar, pero los símbolos significan intersección de bolsas y suma de bolsas (no unión). El valor máximo es 1/2.

{displaystyle J(A,B)={{|Acap B|} over {|Auplus B|}}={{|Acap B|} over {|A|+|B|}}.}

El Distancia de Jaccard, qué medidas distincionessemejanza entre conjuntos de muestra, es complementaria al coeficiente de Jaccard y se obtiene restando el coeficiente de Jaccard de 1, o, equivalentemente, dividiendo la diferencia de los tamaños de la unión y la intersección de dos conjuntos por el tamaño de la unión:

{displaystyle d_{J}(A,B)=1-J(A,B)={{|Acup B|-|Acap B|} over |Acup B|}.}

Una interpretación alternativa de la distancia de Jaccard es como la relación del tamaño de la diferencia simétrica ${displaystyle Atriangle B=(Acup B)-(Acap B)}$ al sindicato. La distancia de Jaccard se utiliza comúnmente para calcular un n × n matriz para agrupar y escalar multidimensionales n conjuntos de muestras.

Esta distancia es una métrica de la colección de todos los conjuntos finitos.

También hay una versión de la distancia de Jaccard para medidas, incluyendo medidas de probabilidad. Si ${displaystyle mu }$ es una medida en un espacio mensurable ${displaystyle X}$ , entonces definimos el coeficiente de Jaccard por

{displaystyle J_{mu }(A,B)={{mu (Acap B)} over {mu (Acup B)}},}

y la distancia Jaccard por

{displaystyle d_{mu }(A,B)=1-J_{mu }(A,B)={{mu (Atriangle B)} over {mu (Acup B)}}.}

Se debe tomar cuidado si ${displaystyle mu (Acup B)=0}$ o ${displaystyle infty }$ , ya que estas fórmulas no están bien definidas en estos casos.

El esquema de hash sensible a la localidad de permutaciones independientes min-wise de MinHash se puede utilizar para calcular de manera eficiente una estimación precisa del coeficiente de similitud de Jaccard de pares de conjuntos, donde cada conjunto está representado por una firma de tamaño constante derivada de los valores mínimos de una función hash.

Similitud de atributos binarios asimétricos

Dados dos objetos, A y B, cada uno con n atributos binarios, el coeficiente de Jaccard es una medida útil de la superposición que A y B comparten sus atributos. Cada atributo de A y B puede ser 0 o 1. El número total de cada combinación de atributos tanto para A como para B se especifican de la siguiente manera:

{displaystyle M_{11}}

representa el número total de atributos donde A y B ambos tienen un valor de 1.

{displaystyle M_{01}}

representa el número total de atributos donde el atributo de A es 0 y el atributo de B 1.

{displaystyle M_{10}}

representa el número total de atributos donde el atributo de A es 1 y el atributo de B es 0.

{displaystyle M_{00}}

representa el número total de atributos donde A y B ambos tienen un valor de 0.

A B	0	1
0	${displaystyle M_{00}}$	${displaystyle M_{10}}$
1	${displaystyle M_{01}}$	${displaystyle M_{11}}$

Cada atributo debe caer en una de estas cuatro categorías, lo que significa que

{displaystyle M_{11}+M_{01}+M_{10}+M_{00}=n.}

El coeficiente de similitud de Jaccard, J, viene dado como

{displaystyle J={M_{11} over M_{01}+M_{10}+M_{11}}.}

La distancia de Jaccard, d_J, se da como

{displaystyle d_{J}={M_{01}+M_{10} over M_{01}+M_{10}+M_{11}}=1-J.}

Se puede hacer inferencia estadística basándose en los coeficientes de similitud de Jaccard y, en consecuencia, en las métricas relacionadas. Dados dos conjuntos de muestras A y B con atributos n, se puede realizar una prueba estadística para ver si una superposición es estadísticamente significativa. La solución exacta está disponible, aunque el cálculo puede resultar costoso a medida que n aumenta. Los métodos de estimación están disponibles ya sea mediante la aproximación de una distribución multinomial o mediante bootstrapping.

Diferencia con el coeficiente de coincidencia simple (SMC)

Cuando se utiliza para atributos binarios, el índice Jaccard es muy similar al coeficiente de coincidencia simple. La diferencia principal es que el SMC tiene el término ${displaystyle M_{00}}$ en su numerador y denominador, mientras que el índice de Jaccard no lo hace. Así, el SMC cuenta ambas presencias mutuas (cuando un atributo está presente en ambos conjuntos) y ausencia mutua (cuando un atributo está ausente en ambos sets) como coincidencias y lo compara con el número total de atributos en el universo, mientras que el índice Jaccard sólo cuenta la presencia mutua como partidos y lo compara con el número de atributos que han sido elegidos por al menos uno de los dos conjuntos.

En el análisis de la cesta de la compra, por ejemplo, la cesta de dos consumidores que deseamos comparar puede contener sólo una pequeña fracción de todos los productos disponibles en la tienda, por lo que el SMC normalmente arrojará valores muy altos de similitudes incluso cuando el Las cestas tienen muy poco parecido, por lo que el índice Jaccard es una medida de similitud más apropiada en ese contexto. Por ejemplo, pensemos en un supermercado con 1000 productos y dos clientes. La canasta del primer cliente contiene sal y pimienta y la canasta del segundo contiene sal y azúcar. En este escenario, la similitud entre las dos cestas medida por el índice de Jaccard sería 1/3, pero la similitud llega a 0,998 utilizando el SMC.

En otros contextos, donde 0 y 1 contienen información equivalente (simetría), el SMC es una mejor medida de similitud. Por ejemplo, los vectores de variables demográficas almacenados en variables ficticias, como el género, se compararían mejor con el SMC que con el índice de Jaccard, ya que el impacto del género en la similitud debería ser igual, independientemente de si lo masculino se define como 0 y lo femenino. como un 1 o al revés. Sin embargo, cuando tenemos variables ficticias simétricas, se podría replicar el comportamiento del SMC dividiendo las ficticias en dos atributos binarios (en este caso, masculino y femenino), transformándolos así en atributos asimétricos, permitiendo el uso del índice Jaccard sin introduciendo cualquier sesgo. Sin embargo, el SMC sigue siendo más eficiente computacionalmente en el caso de variables ficticias simétricas, ya que no requiere agregar dimensiones adicionales.

Similitud y distancia ponderada de Jaccard

Si ${displaystyle mathbf {x} =(x_{1},x_{2},ldotsx_{n})}$ y ${displaystyle mathbf {y} =(y_{1},y_{2},ldotsy_{n})}$ son dos vectores con todo real ${displaystyle x_{i},y_{i}geq 0}$ , entonces su coeficiente de semejanza de Jaccard (también conocido entonces como semejanza de Ruzicka) se define como

{displaystyle J_{mathcal {W}}(mathbf {x}mathbf {y})={frac {sum _{i}min(x_{i},y_{i})}{sum _{i}max(x_{i},y_{i})}},}

y distancia de Jaccard (también conocida como distancia de Soergel)

{displaystyle d_{J{mathcal {W}}}(mathbf {x}mathbf {y})=1-J_{mathcal {W}}(mathbf {x}mathbf {y}).}

Con más generalidad, si ${displaystyle f}$ y ${displaystyle g}$ son dos funciones medibles no negativas en un espacio mensurable ${displaystyle X}$ con medida ${displaystyle mu }$ , entonces podemos definir

{displaystyle J_{mathcal {W}}(f,g)={frac {int min(f,g)dmu }{int max(f,g)dmu }},}

Donde ${displaystyle max }$ y ${displaystyle min }$ son operadores punteros. Entonces la distancia de Jaccard es

{displaystyle d_{J{mathcal {W}}}(f,g)=1-J_{mathcal {W}}(f,g).}

Entonces, por ejemplo, para dos conjuntos mensurables ${displaystyle A,Bsubseteq X}$ , tenemos ${displaystyle J_{mu }(A,B)=J(chi _{A},chi _{B}),}$ Donde ${displaystyle chi _{A}}$ y ${displaystyle chi _{B}}$ son las funciones características del conjunto correspondiente.

Probability Jaccard semejanza y distancia

La similitud de Jaccard ponderada descrita anteriormente generaliza el índice de Jaccard a vectores positivos, donde un conjunto corresponde a un vector binario dado por la función indicadora, es decir. ${displaystyle x_{i}in {0,1}}$ . Sin embargo, no generaliza el índice de Jaccard a las distribuciones de probabilidad, donde un conjunto corresponde a una distribución de probabilidad uniforme, es decir,.

{displaystyle x_{i}={begin{cases}{frac {1}{|X|}}&iin X\0&{text{otherwise}}end{cases}}}

Siempre es menos si los conjuntos difieren en tamaño. Si $|Y|}" xmlns="http://www.w3.org/1998/Math/MathML">SilencioXSilencio■SilencioYSilencio{displaystyle Silencioso|Y|}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f80f01e262afdfc81608fd43cfd047898e3b84f7" style="vertical-align: -0.838ex; width:9.439ex; height:2.843ex;"/>$ , y ${displaystyle x_{i}=mathbf {1} _{X}(i)/|X|,y_{i}=mathbf {1} _{Y}(i)/|Y|}$ entonces

<math alttext="{displaystyle J_{mathcal {W}}(x,y)={frac {|Xcap Y|}{|Xsetminus Y|+|X|}}JW()x,Sí.)=SilencioX∩ ∩ YSilencioSilencioX∖ ∖ YSilencio+SilencioXSilencioc)J()X,Y).{displaystyle J_{mathcal {W}(x,y)={frac Oh, Dios mío. Y sobrevivir a la muerte<img alt="{displaystyle J_{mathcal {W}}(x,y)={frac {|Xcap Y|}{|Xsetminus Y|+|X|}}

En cambio, una generalización continua entre las distribuciones de probabilidad y sus correspondientes conjuntos de soporte es

{displaystyle J_{mathcal {P}}(x,y)=sum _{x_{i}neq 0,y_{i}neq 0}{frac {1}{sum _{j}max left({frac {x_{j}}{x_{i}}},{frac {y_{j}}{y_{i}}}right)}}}

que se llama "Probabilidad" Jaccard. Tiene los siguientes límites contra el Jaccard Weighted en vectores de probabilidad.

{displaystyle J_{mathcal {W}}(x,y)leq J_{mathcal {P}}(x,y)leq {frac {2J_{mathcal {W}}(x,y)}{1+J_{mathcal {W}}(x,y)}}}

Aquí el límite superior es el coeficiente (pesado) Sørensen-Dice. La distancia correspondiente, ${displaystyle 1-J_{mathcal {P}}(x,y)}$ , es una métrica sobre las distribuciones de probabilidad, y un pseudo-métrico sobre vectores no negativos.

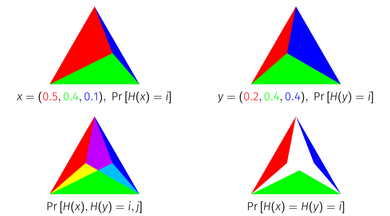
El índice de probabilidad de Jaccard tiene una interpretación geométrica como el área de una intersección de simplices. Cada punto en una unidad ${displaystyle k}$ -simplex corresponde a una distribución de probabilidad en ${displaystyle k+1}$ elementos, porque la unidad ${displaystyle k}$ -simplex es el conjunto de puntos en ${displaystyle k+1}$ dimensiones que suman a 1. Para obtener el índice de probabilidad Jaccard geométricamente, representan una distribución de probabilidad como el simplex de la unidad dividido en los simplices sub de acuerdo a la masa de cada elemento. Si superpones dos distribuciones representadas de esta manera encima de las otras, e intersectas los simplices correspondientes a cada elemento, el área que permanece es igual al Índice de Probability Jaccard de las distribuciones.

Optimality of the Probability Jaccard Index

Considere el problema de construir variables aleatorias tales que colliden entre sí tanto como sea posible. Eso es, si ${displaystyle Xsim x}$ y ${displaystyle Ysim y}$ , nos gustaría construir ${displaystyle X}$ y ${displaystyle Y}$ para maximizar ${displaystyle Pr[X=Y]}$ . Si miramos sólo dos distribuciones ${displaystyle x,y}$ en aislamiento, el más alto ${displaystyle Pr[X=Y]}$ podemos lograrlo ${displaystyle 1-{text{TV}}(x,y)}$ Donde ${displaystyle {text{TV}}}$ es la distancia total de la variación. Sin embargo, supongamos que no sólo estábamos preocupados con maximizar ese par en particular, supongamos que nos gustaría maximizar la probabilidad de colisión de cualquier par arbitrario. Uno podría construir un número infinito de variables aleatorias una para cada distribución ${displaystyle x}$ , y tratar de maximizar ${displaystyle Pr[X=Y]}$ para todos los pares ${displaystyle x,y}$ . En un sentido bastante fuerte descrito a continuación, el índice de probabilidad Jaccard es una manera óptima de alinear estas variables aleatorias.

Para cualquier método de muestreo ${displaystyle G}$ y distribuciones discretas ${displaystyle x,y}$ , si $J_{mathcal {P}}(x,y)}" xmlns="http://www.w3.org/1998/Math/MathML">Pr[G()x)=G()Sí.)]■JP()x,Sí.){displaystyle Pr[G(x)=G(y)] confianzaJ_{mathcal {P}(x,y)}J_{mathcal {P}}(x,y)}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d51bcb8456e58c7bfdc742dc68a54693ed5dfacf" style="vertical-align: -0.838ex; width:27.798ex; height:2.843ex;"/>$ entonces para algunos ${displaystyle z}$ Donde $J_{mathcal {P}}(x,y)}" xmlns="http://www.w3.org/1998/Math/MathML">JP()x,z)■JP()x,Sí.){displaystyle J_{mathcal {}(x,z) ConfíoJ_{mathcal {P}(x,y)}J_{mathcal {P}}(x,y)}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c89e01bc62b77de3b856828f0d87ce662ce9ae81" style="vertical-align: -0.838ex; width:19.142ex; height:2.843ex;"/>$ y $J_{mathcal {P}}(x,y)}" xmlns="http://www.w3.org/1998/Math/MathML">JP()Sí.,z)■JP()x,Sí.){displaystyle J_{mathcal {}(y,z) ConfíoJ_{mathcal {P}(x,y)}J_{mathcal {P}}(x,y)}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3234eceee4240845fb0873ca3f433f9625df49c3" style="vertical-align: -0.838ex; width:18.968ex; height:2.843ex;"/>$ , o $<math alttext="{displaystyle Pr[G(x)=G(z)]Pr[G()x)=G()z)]c)JP()x,z){displaystyle Pr[G(x)=G(z)] <img alt="{displaystyle Pr[G(x)=G(z)]$ o $<math alttext="{displaystyle Pr[G(y)=G(z)]Pr[G()Sí.)=G()z)]c)JP()Sí.,z){displaystyle Pr[G(y)=G(z)] <img alt="{displaystyle Pr[G(y)=G(z)]$ .

Es decir, ningún método de muestreo puede lograr más colisiones que ${displaystyle J_{mathcal {P}}}$ en un par sin conseguir menos colisiones que ${displaystyle J_{mathcal {P}}}$ en otro par, donde el par reducido es más similar bajo ${displaystyle J_{mathcal {P}}}$ que el par aumentado. Este teorema es verdadero para el índice de Jaccard de conjuntos (si se interpreta como distribuciones uniformes) y la probabilidad Jaccard, pero no del Jaccard ponderado. (El teorema utiliza la palabra "método de muestreo" para describir una distribución conjunta sobre todas las distribuciones en un espacio, porque deriva del uso de algoritmos de mezcla ponderada que lo consiguen como su probabilidad de colisión.)

Este teorema tiene una prueba visual de distribuciones de tres elementos utilizando la representación simplex.

Similitud y distancia de Tanimoto

Varias formas de funciones descritas como similitud de Tanimoto y distancia de Tanimoto ocurren en la literatura y en Internet. La mayoría de estos son sinónimos de similitud de Jaccard y distancia de Jaccard, pero algunos son matemáticamente diferentes. Muchas fuentes citan un informe técnico de IBM como referencia fundamental. El informe está disponible en varias bibliotecas.

En "Un programa informático para clasificar plantas", publicado en octubre de 1960, se proporciona un método de clasificación basado en una relación de similitud y una función de distancia derivada. Parece que esta es la fuente más autorizada para conocer el significado de los términos "similitud de Tanimoto" y "Distancia Tanimoto". La relación de similitud es equivalente a la similitud de Jaccard, pero la función de distancia no es la misma que la distancia de Jaccard.

Definiciones de similitud y distancia de Tanimoto

En ese artículo, una "relación de similitud" se proporciona en mapas de bits, donde cada bit de una matriz de tamaño fijo representa la presencia o ausencia de una característica en la planta que se está modelando. La definición de la relación es el número de bits comunes, dividido por el número de bits establecidos (es decir, distinto de cero) en cualquiera de las muestras.

Presentado en términos matemáticos, si muestras X y Y son chiflados, ${displaystyle X_{i}}$ es it bit of X, y ${displaystyle landlor }$ son bitwise y, o operadores respectivamente, luego la relación de similitud ${displaystyle T_{s}}$ es

{displaystyle T_{s}(X,Y)={frac {sum _{i}(X_{i}land Y_{i})}{sum _{i}(X_{i}lor Y_{i})}}}

Si cada muestra se modela como un conjunto de atributos, este valor es igual al coeficiente de Jaccard de los dos conjuntos. Jaccard no se cita en el artículo y parece probable que los autores no lo supieran.

Tanimoto continúa definiendo un "coeficiente de distancia" basado en esta relación, definida para mapas de bits con similitud distinta de cero:

{displaystyle T_{d}(X,Y)=-log _{2}(T_{s}(X,Y))}

Este coeficiente no es, deliberadamente, una métrica de distancia. Se elige para permitir la posibilidad de que dos especímenes, que son bastante diferentes entre sí, sean similares a un tercero. Es fácil construir un ejemplo que refute la propiedad de la desigualdad triangular.

Otras definiciones de distancia Tanimoto

La distancia de Tanimoto es a menudo referida, erróneamente, como sinónimo de distancia de Jaccard ${displaystyle 1-T_{s}}$ . Esta función es una métrica de distancia adecuada. "Tanimoto Distancia" a menudo se declara como una métrica de distancia adecuada, probablemente debido a su confusión con la distancia de Jaccard.

Si la similitud de Jaccard o Tanimoto se expresa sobre un vector de bits, entonces se puede escribir como

{displaystyle f(A,B)={frac {Acdot B}{|A|^{2}+|B|^{2}-Acdot B}}}

donde el mismo cálculo se expresa en términos de producto escalar vectorial y magnitud. Esta representación se basa en el hecho de que, para un vector de bits (donde el valor de cada dimensión es 0 o 1), entonces

{displaystyle Acdot B=sum _{i}A_{i}B_{i}=sum _{i}(A_{i}land B_{i})}

{displaystyle |A|^{2}=sum _{i}A_{i}^{2}=sum _{i}A_{i}.}

Esta es una representación potencialmente confusa, porque la función expresada sobre los vectores es más general, a menos que su dominio esté explícitamente restringido. Propiedades de ${displaystyle T_{s}}$ no se extiende necesariamente ${displaystyle f}$ . En particular, la función de diferencia ${displaystyle 1-f}$ no preserva la desigualdad del triángulo, y por lo tanto no es una distancia métrica adecuada, mientras que ${displaystyle 1-T_{s}}$ Lo es.

Existe un peligro real de que la combinación de "Tanimoto Distancia" que se define utilizando esta fórmula, junto con la afirmación "Tanimoto Distancia es una distancia métrica adecuada" lleve a la conclusión falsa de que la función ${displaystyle 1-f}$ es de hecho una distancia métrica sobre vectores o multisets en general, mientras que su uso en la búsqueda de similitudes o algoritmos de agrupación puede no producir resultados correctos.

Lipkus utiliza una definición de la similitud Tanimoto que es equivalente a ${displaystyle f}$ , y se refiere a la distancia Tanimoto como la función ${displaystyle 1-f}$ . Sin embargo, en el documento queda claro que el contexto está restringido por el uso de un vector de ponderación (positivo) ${displaystyle W}$ tal que, para cualquier vector A siendo considerado, ${displaystyle A_{i}in {0,W_{i}}.}$ Bajo estas circunstancias, la función es una métrica de distancia adecuada, y por lo tanto un conjunto de vectores gobernados por tal vector de peso forma un espacio métrico bajo esta función.

Índice de Jaccard en matrices de confusión de clasificación binaria

En las matrices de confusión empleadas para la clasificación binaria, el índice de Jaccard se puede enmarcar en la siguiente fórmula:

{displaystyle {text{Jaccard index}}={frac {TP}{TP+FP+FN}}}

donde TP son los verdaderos positivos, FP los falsos positivos y FN los falsos negativos.

Más resultados...