Impedancia de onda

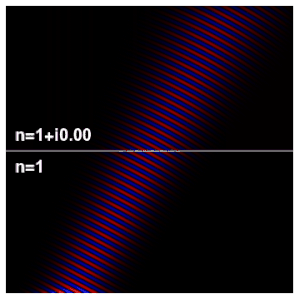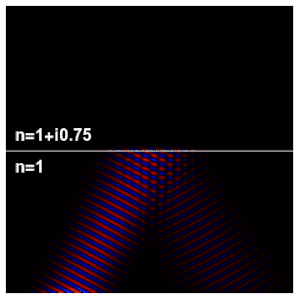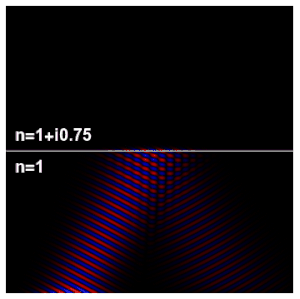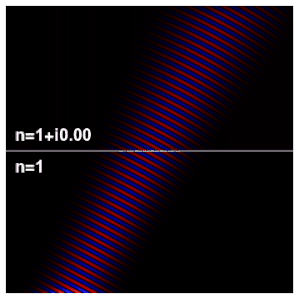
La impedancia de onda de una onda electromagnética es la relación de las componentes transversales de los campos eléctrico y magnético (siendo las componentes transversales aquellas que forman ángulos rectos con la dirección de propagación). Para una onda plana electromagnética transversal (TEM) que viaja a través de un medio homogéneo, la impedancia de la onda es en todas partes igual a la impedancia intrínseca del medio. En particular, para una onda plana que viaja a través del espacio vacío, la impedancia de la onda es igual a la impedancia del espacio libre. Se utiliza el símbolo Z para representarlo y se expresa en unidades de ohmios. Se puede usar el símbolo η (eta) en lugar de Z para la impedancia de onda para evitar confusiones con la impedancia eléctrica.

Definición

Para evitar las reflexiones, la impedancia de dos medios debe coincidir. Por otro lado, incluso si la parte real del índice refractivo es la misma, pero uno tiene un gran coeficiente de absorción, el desajuste de impedancia hará que la interfaz sea altamente reflexiva.

La impedancia de onda viene dada por

Z=E0− − ()x)H0− − ()x){displaystyle Z={E_{0}{-}(x) over H_{0}{-}(x)}

Donde E0− − ()x){displaystyle E_{0} {-}(x)} es el campo eléctrico y H0− − ()x){displaystyle H_{0} {-}(x)} es el campo magnético, en representación de faasor. La impedancia es, en general, un número complejo.

En términos de los parámetros de una onda electromagnética y el medio por el que viaja, la impedancia de la onda viene dada por

Z=j⋅ ⋅ μ μ σ σ +j⋅ ⋅ ε ε {displaystyle Z={sqrt {jomega mu over sigma +jomega varepsilon }

donde μ es la permeabilidad magnética, ε es la permitividad eléctrica (real) y σ es la conductividad eléctrica del material de la onda está transitando (correspondiente a la componente imaginaria de la permitividad multiplicada por omega). En la ecuación, j es la unidad imaginaria y ω es la frecuencia angular de la onda. Al igual que la impedancia eléctrica, la impedancia es una función de la frecuencia. En el caso de un dieléctrico ideal (donde la conductividad es cero), la ecuación se reduce al número real

Z=μ μ ε ε .{displaystyle Z={sqrt {mu over varepsilon }}

En espacio libre

En el espacio libre, la impedancia de onda de las ondas planas es:

Z0=μ μ 0ε ε 0{displaystyle Z_{0}={sqrt {frac # ¿Qué? ♪♪

(donde ε₀ es la constante de permitividad en el espacio libre y μ₀ es la constante de permeabilidad en espacio libre). Ahora, desde

c0=1μ μ 0ε ε 0=299,792,458m/s{displaystyle c_{0}={frac {1}{sqrt {mu} _{0}varepsilon - Sí. (por la definición SI del metro),

Z0=μ μ 0c0{displaystyle Z_{0}=mu ¿Qué?.

De ahí que el valor dependa esencialmente de μ μ 0{displaystyle mu _{0}}. Hasta el 20 de mayo de 2019, μ μ 0=4π π × × 10− − 7H/m{displaystyle mu _{0}=4pitimes 10^{-7}{text{H/m}}, por lo tanto

Z0=376.73031346177...... Ω Ω .. 120π π Ω Ω {displaystyle Z_{0}=376.73031346177ldots ~Omega approx 120pi - Omega..

El valor actualmente aceptado Z0{displaystyle Z_{0} es

Z0=376.730313668()57)Ω Ω {displaystyle Z_{0}=376.730313668(57)~Omega }.

En un dieléctrico ilimitado

En una dieléctrica isotrópica y homogénea con propiedades magnéticas insignificantes, es decir. μ μ =μ μ 0=4π π × × 10− − 7{displaystyle mu =mu _{0}=4pitimes 10^{-7} H/m y ε ε =ε ε r× × 8.854× × 10− − 12{displaystyle varepsilon =varepsilon ¿Qué? F/m. Entonces, el valor de la impedancia de onda en una perfecta dielectrica es

Z=μ μ ε ε =μ μ 0ε ε 0ε ε r=Z0ε ε r.. 377ε ε rΩ Ω {displaystyle Z={sqrt {mu over varepsilon }={sqrt {mu _{0} over varepsilon _{0}varepsilon {cHFF}={Z_{0} {sqrt {varepsilon }_{r}approx {377 over {varepsilon Oh, Dios.,

Donde ε ε r{displaystyle varepsilon _{r} es la relativa constante dieléctrica.

En una guía de ondas

Para cualquier guía de onda en forma de tubo de metal hueco, (como guía rectangular, guía circular o guía de doble canto), la impedancia de onda de una onda de viaje depende de la frecuencia f{displaystyle f}, pero es lo mismo en todo el guía. Para los modos transversos eléctricos (TE) de propagación la impedancia de onda es:

Z=Z01− − ()fcf)2(Modos TTE),{displaystyle Z={frac {Z_{0}{sqrt {1-left({frac} {f}}}qquad {mbox{(TE modes)}}}}

donde f_c es la frecuencia de corte del modo, y para los modos de propagación magnéticos transversales (TM), la impedancia de onda es:

Z=Z01− − ()fcf)2(Modos TM){displaystyle Z=Z_{0}{sqrt {1-left({frac {f_{c} {f}}}qquad {mbox{(TM modes)}}}

Por encima del corte (f > f_c ), la impedancia es real (resistiva) y la onda transporta energía. Por debajo del corte, la impedancia es imaginaria (reactiva) y la onda es evanescente. Estas expresiones ignoran el efecto de pérdida resistiva en las paredes de la guía de ondas. Para una guía de ondas completamente llena con un medio dieléctrico homogéneo, se aplican expresiones similares, pero con la impedancia de onda del medio reemplazando Z₀. La presencia del dieléctrico también modifica la frecuencia de corte f_c.

Para una guía de ondas o una línea de transmisión que contenga más de un tipo de medio dieléctrico (como una microcinta), la impedancia de la onda variará en general a lo largo de la sección transversal de la línea.