IEEE754-1985
IEEE 754-1985 era un estándar de la industria para representar números de coma flotante en computadoras, adoptado oficialmente en 1985 y reemplazado en 2008 por IEEE 754-2008, y luego nuevamente en 2019 por una revisión menor IEEE 754-2019. Durante sus 23 años, fue el formato más utilizado para el cálculo de punto flotante. Se implementó en software, en forma de bibliotecas de punto flotante, y en hardware, en las instrucciones de muchas CPU y FPU. El primer circuito integrado en implementar el borrador de lo que se convertiría en IEEE 754-1985 fue el Intel 8087.
IEEE 754-1985 representa números en binario y proporciona definiciones para cuatro niveles de precisión, de los cuales los dos más utilizados son:
| Nivel | Width | Rango a toda precisión | Precisión |
|---|---|---|---|
| Precisión sencilla | 32 bits | ±1.18×10,38 - 38 a ±3,4×1038 | Aproximadamente 7 dígitos decimales |
| Doble precisión | 64 bits | ±2,23×10−308 a ± 1,80×10308 | Aproximadamente 16 dígitos decimales |
El estándar también define representaciones para infinito positivo y negativo, un "cero negativo", cinco excepciones para manejar resultados no válidos como la división por cero, valores especiales llamados NaN para representar esas excepciones, números anormales para representar números más pequeño que el que se muestra arriba, y cuatro modos de redondeo.
Representación de números
Los números de punto flotante en formato IEEE 754 constan de tres campos: un bit de signo, un exponente sesgado y una fracción. El siguiente ejemplo ilustra el significado de cada uno.
El número decimal 0,1562510 representado en binario es 0,001012 (es decir, 1/8 + 1/32). (Los subíndices indican la base numérica.) Análogamente a la notación científica, donde los números se escriben para tener un solo dígito distinto de cero a la izquierda del punto decimal, reescribimos este número para que tenga un solo bit 1 a la izquierda del & #34;punto binario". Simplemente multiplicamos por la potencia apropiada de 2 para compensar el desplazamiento de los bits dejados por tres posiciones:
- 0,001012=1.012× × 2− − 3{displaystyle 0,00101_{2}=1.01_{2}times 2^{-3}
Ahora podemos leer la fracción y el exponente: la fracción es.012 y el exponente es −3.
Como se ilustra en las imágenes, los tres campos en la representación IEEE 754 de este número son:
- Signatura = 0, porque el número es positivo. (1 indica negativo.)
- exponente sesgado = −3 + los "bias". In precisión única, el sesgo es 127, así que en este ejemplo el exponente sesgado es 124; en doble precisión, el sesgo es 1023, por lo que el exponente sesgado en este ejemplo es 1020.
- fracción =.01000...2.
IEEE 754 añade un sesgo al exponente para que, en muchos casos, los números puedan compararse cómodamente con el mismo hardware que compara los enteros con signo en complemento a 2. Usando un exponente sesgado, el menor de dos números de coma flotante positivos resultará "menor que" el mayor siguiendo el mismo orden que para los enteros de signo y magnitud. Si dos números de punto flotante tienen signos diferentes, la comparación de signo y magnitud también funciona con exponentes sesgados. Sin embargo, si ambos números de punto flotante con exponente sesgado son negativos, entonces se debe invertir el orden. Si el exponente se representara como, por ejemplo, un número en complemento a 2, la comparación para ver cuál de los dos números es mayor no sería tan conveniente.
El bit 1 inicial se omite ya que todos los números, excepto el cero, comienzan con un 1 inicial; el 1 inicial está implícito y en realidad no necesita almacenarse, lo que brinda un poco más de precisión de forma "gratis".
Cero
El número cero se representa especialmente:
- Signatura = 0 para cero positivo, 1 para cero negativo.
- exponente sesgado = 0.
- fracción = 0.
Números desnormalizados
Las representaciones numéricas descritas anteriormente se denominan normalizadas, lo que significa que el dígito binario inicial implícito es un 1. Para reducir la pérdida de precisión cuando se produce un desbordamiento, IEEE 754 incluye la capacidad de representar fracciones más pequeñas de lo que es posible en la representación normalizada, haciendo que el dígito inicial implícito sea 0. Estos números se denominan denormales. No incluyen tantos dígitos significativos como un número normalizado, pero permiten una pérdida gradual de precisión cuando el resultado de una operación no es exactamente cero pero está demasiado cerca de cero para ser representado por un número normalizado.
Un número anormal se representa con un exponente sesgado de todos los 0 bits, lo que representa un exponente de −126 en precisión simple (no −127), o −1022 en precisión doble (no −1023). Por el contrario, el exponente sesgado más pequeño que representa un número normal es 1 (ver ejemplos a continuación).
Representación de no números
El campo de exponente sesgado se llena con todos los bits 1 para indicar infinito o un resultado no válido de un cálculo.
Infinito positivo y negativo
El infinito positivo y negativo se representan así:
- Signatura = 0 para el infinito positivo, 1 para el infinito negativo.
- exponente sesgado = todos 1 bits.
- fracción = todos 0 bits.
NaN
Algunas operaciones de aritmética de coma flotante no son válidas, como sacar la raíz cuadrada de un número negativo. El acto de obtener un resultado no válido se denomina excepción de punto flotante. Un resultado excepcional se representa mediante un código especial llamado NaN, por "No es un número". Todos los NaN en IEEE 754-1985 tienen este formato:
- Signatura = 0 o 1.
- exponente sesgado = todos 1 bits.
- fracción = cualquier cosa excepto los 0 bits (ya que todos los 0 bits representa infinito).
Alcance y precisión
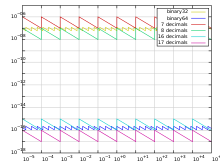
La precisión se define como la diferencia mínima entre dos representaciones de mantisa sucesivas; así es una función sólo en la mantisa; mientras que la brecha se define como la diferencia entre dos números sucesivos.
Precisión simple
Los números de precisión simple ocupan 32 bits. En precisión simple:
- Los números positivos y negativos más cercanos a cero (representados por el valor desnormalizado con todos los 0s en el campo exponente y el valor binario 1 en el campo de la fracción) son
- ±2,23 a 23 × 2−126 ± 1.40130×10,45 - 45
- Los números normalizados positivos y negativos más cercanos a cero (representados con el valor binario 1 en el campo exponente y 0 en el campo de la fracción) son
- ±1 × 2−126 ±1.17549×10,38 - 38
- Los números negativos positivos finitos y finitos más lejos de cero (representados por el valor con 254 en el campo exponente y los 1s en el campo de la fracción) son
- ± 2 - 2,23 a 23) × 2127 ±3.40282×1038
Algunos valores de rango y brecha de ejemplo para exponentes dados en precisión simple:
| Exponente real (sin prejuicios) | Exp (biased) | Mínimo | Máximo | Gap |
|---|---|---|---|---|
| −1 | 126 | 0.5 | Entendido 0,9999940395 | ■ 5.96046e-8 |
| 0 | 127 | 1 | ■ 1.999880791 | ■ 1.19209e-7 |
| 1 | 128 | 2 | Entendido. | ■ 2.38419e-7 |
| 2 | 129 | 4 | Entendido. | ■ 4.76837e-7 |
| 10 | 137 | 1024 | Entendido 2047.999877930 | ■ 1.22070e-4 |
| 11 | 138 | 2048 | ■ 4095.999755859 | ■ 2.44141e-4 |
| 23 | 150 | 8388608 | 16777215 | 1 |
| 24 | 151 | 16777216 | 33554430 | 2 |
| 127 | 254 | ■ 1.70141e38 | Entendido. | ■ 2.02824e31 |
Por ejemplo, 16 777 217 no se puede codificar como un flotante de 32 bits, ya que se redondeará a 16 777 216. Esto muestra por qué la aritmética de punto flotante no es adecuada para el software de contabilidad. Sin embargo, todos los enteros dentro del rango representable que son una potencia de 2 se pueden almacenar en un flotante de 32 bits sin redondeo.
Doble precisión
Los números de doble precisión ocupan 64 bits. En doble precisión:
- Los números positivos y negativos más cercanos a cero (representados por el valor desnormalizado con todos los 0s en el campo Exp y el valor binario 1 en el campo Fracción) son
- ±2−52 × 2−10-22 ±4.94066×10−324
- Los números positivos y negativos normalizados más cercanos a cero (representados con el valor binario 1 en el campo Exp y 0 en el campo de la fracción) son
- ±1 × 2−10-22 ±2.22507×10−308
- Los números negativos positivos finitos y finitos más lejos de cero (representados por el valor con 2046 en el campo Exp y los 1s en el campo de la fracción) son
- ± 2 - 2−52) × 21023 ±1.79769×10308
Algunos valores de rango y brecha de ejemplo para exponentes dados en doble precisión:
| Exponente real (sin prejuicios) | Exp (biased) | Mínimo | Máximo | Gap |
|---|---|---|---|---|
| −1 | 1022 | 0.5 | Entendido. | ■ 1.11022e-16 |
| 0 | 1023 | 1 | ■ 1.999999999999999777955 | ■ 2.22045e-16 |
| 1 | 1024 | 2 | Entendido. | Entendido 4.44089e-16 |
| 2 | 1025 | 4 | Entendido 7.999999999999999111822 | ■ 8.88178e-16 |
| 10 | 1033 | 1024 | Entendido 2047.999999999999772626 | ■ 2.27374e-13 |
| 11 | 1034 | 2048 | ■ 4095.999999999999545253 | ■ 4.54747e-13 |
| 52 | 1075 | 4503599627370496 | 90071992540991 | 1 |
| 53 | 1076 | 90071992540992 | 18014398509481982 | 2 |
| 1023 | 2046 | ■ 8.98847e307 | ■ 1.79769e308 | ■ 1.99584e292 |
Formatos extendidos
El estándar también recomienda el uso de formato(s) extendido(s) para realizar cálculos internos con una precisión mayor que la requerida para el resultado final, para minimizar los errores de redondeo: el estándar solo especifica los requisitos mínimos de precisión y exponente para dichos formatos.. El formato extendido x87 de 80 bits es el formato extendido más comúnmente implementado que cumple con estos requisitos.
Ejemplos
Estos son algunos ejemplos de representaciones IEEE 754 de precisión simple:
| Tipo | Signatura | Exponente real | Exp (biased) | Campo expositivo | Campo de fractura | Valor |
|---|---|---|---|---|---|---|
| Cero | 0 | −126 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | 0,0 |
| Negativo cero | 1 | −126 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | 0.0− |
| Uno | 0 | 0 | 127 | 0111 1111 | 000 0000 0000 0000 0000 0000 | 1.0 |
| Menos Uno | 1 | 0 | 127 | 0111 1111 | 000 0000 0000 0000 0000 0000 | 1.0− |
| Número desnormalizado más pequeño | * | −126 | 0 | 0000 0000 | 000 0000 0000 0000 | ±2,23 a 23 × 2−126 = ±2−149 ±1.4×10,45 - 45 |
| Número desnormalizado "Middle" | * | −126 | 0 | 0000 0000 | 100 0000 0000 0000 0000 0000 | ±2−1 × 2−126 = ±2−127 ± 5,88×10−39− |
| Número desnormalizado más grande | * | −126 | 0 | 0000 0000 | 111 1111 1111 1111 1111 1111 1111 1111 | ± 1 - 2,23 a 23) × 2−126 ± 1.18×10,38 - 38 |
| Número normalizado más pequeño | * | −126 | 1 | 0000 0001 | 000 0000 0000 0000 0000 0000 | ±2−126 ± 1.18×10,38 - 38 |
| Número normalizado más grande | * | 127 | 254 | 1111 1110 | 111 1111 1111 1111 1111 1111 1111 1111 | ± 2 - 2,23 a 23) × 2127 ± 3,4×1038 |
| Infinidad positiva | 0 | 128 | 255 | 1111 1111 | 000 0000 0000 0000 0000 0000 | + |
| Infinidad negativa | 1 | 128 | 255 | 1111 1111 | 000 0000 0000 0000 0000 0000 | JUEGO |
| No. | * | 128 | 255 | 1111 1111 | no cero | Nan |
| * Sign bit puede ser 0 o 1. | ||||||
Comparar números de coma flotante
Cada combinación de bits posible es un NaN o un número con un valor único en el sistema de números reales afinemente extendido con su orden asociado, excepto las dos combinaciones de bits para el cero negativo y el cero positivo, que a veces requieren una atención especial (vea abajo). La representación binaria tiene la propiedad especial de que, excluyendo los NaN, dos números cualesquiera pueden compararse como enteros de signo y magnitud (se aplican problemas de endianness). Al comparar como enteros en complemento a 2: si los bits de signo difieren, el número negativo precede al número positivo, por lo que el complemento a 2 da el resultado correcto (excepto que el cero negativo y el cero positivo deben considerarse iguales). Si ambos valores son positivos, la comparación del complemento a 2 vuelve a dar el resultado correcto. De lo contrario (dos números negativos), la ordenación correcta de FP es la opuesta a la ordenación del complemento a 2.
Los errores de redondeo inherentes a los cálculos de punto flotante pueden limitar el uso de comparaciones para comprobar la igualdad exacta de los resultados. Elegir un rango aceptable es un tema complejo. Una técnica común es utilizar un valor épsilon de comparación para realizar comparaciones aproximadas. Dependiendo de cuán indulgentes sean las comparaciones, los valores comunes incluyen 1e-6 o 1e-5 para precisión simple y 1e-14 para precisión doble. -precisión. Otra técnica común es ULP, que verifica cuál es la diferencia en los dígitos del último lugar, verificando efectivamente cuántos pasos se encuentran entre los dos valores.
Aunque el cero negativo y el cero positivo generalmente se consideran iguales a efectos de comparación, algunos operadores relacionales del lenguaje de programación y construcciones similares los tratan como distintos. De acuerdo con la especificación del lenguaje Java, los operadores de comparación e igualdad los tratan como iguales, pero Math.min() y Math.max() los distinguen (oficialmente comenzando con la versión de Java 1.1 pero en realidad con 1.1.1), al igual que los métodos de comparación equals(), compareTo() e incluso compare() de clases Flotante y Doble.
Redondeo de números de coma flotante
El estándar IEEE tiene cuatro modos de redondeo diferentes; el primero es el predeterminado; los otros se llaman redondeos dirigidos.
- Round to Nearest – rondas al valor más cercano; si el número cae a mitad de camino se redondea al valor más cercano con un bit aún (cero) menos significativo, lo que significa que se redondea el 50% del tiempo (en IEEE 754-2008 este modo se llama redonda TiesToEven para distinguirlo de otro modo redondo-a-resto)
- Ronda hacia 0 – redondeo dirigido hacia cero
- Redondo hacia +∞ – redondeo dirigido hacia el infinito positivo
- Redondo hacia − – redondeo dirigido hacia el infinito negativo.
Extendiendo los números reales
El estándar IEEE emplea (y amplía) el sistema de números reales extendido por afinidad, con infinitos positivos y negativos separados. Durante la redacción, hubo una propuesta para que el estándar incorporara el sistema de números reales proyectivamente extendido, con un único infinito sin signo, proporcionando a los programadores una opción de selección de modo. Sin embargo, con el fin de reducir la complejidad del estándar final, se eliminó el modo proyectivo. Los coprocesadores de coma flotante Intel 8087 e Intel 80287 admiten este modo proyectivo.
Funciones y predicados
Operaciones estándar
Se deben proporcionar las siguientes funciones:
- Añadir, restar, multiplicar, dividir
- Base cuadrada
- Permanecedor de punto flotante. Esto no es como una operación de modulo normal, puede ser negativo para dos números positivos. Devuelve el valor exacto de x–(round(x/y)·y).
- Redondeado a entero más cercano. Para redondeo no dirigido cuando a mitad de camino entre dos enteros el entero es elegido.
- Operaciones de comparación. Además de los resultados más obvios, IEEE 754 define que −∞ = −∞, +∞ = LGBT y xل
NaNpara cualquier x (incluidasNaN).
Funciones y predicados recomendados
copysign(x,y)devuelve x con la señal de y, asíabs(x)igualescopysign(x,1.0). Esta es una de las pocas operaciones que opera en una NaN de una manera parecido a la aritmética. La funcióncopysignes nuevo en el estándar C99.- −x devuelve x con el signo revertido. Esto es diferente de 0−x en algunos casos, especialmente cuando x es 0. Así que −(0) es −0, pero el signo de 0−0 depende del modo de redondeo.
scalb(y, N)logb(x)finite(x)a predicate for "x is a finite value", equivalent to −Inf Identificado xisnan(x)un predicado para "x es un NaN", equivalente a "x ‡ x"x y, que resulta tener un comportamiento diferente a NO(x = y) debido a NaN.unordered(x, y)es cierto cuando "x está sin orden con y", es decir, x o y es una NaN.class(x)nextafter(x,y)devuelve el siguiente valor representable de x en la dirección hacia y
Historia
En 1976, Intel estaba iniciando el desarrollo de un coprocesador de punto flotante. Intel esperaba poder vender un chip que contuviera buenas implementaciones de todas las operaciones que se encuentran en las bibliotecas de software de matemáticas muy variadas.
John Palmer, quien dirigió el proyecto, creía que el esfuerzo debería estar respaldado por un estándar que unificara las operaciones de punto flotante en procesadores dispares. Se puso en contacto con William Kahan de la Universidad de California, quien había ayudado a mejorar la precisión de las calculadoras de Hewlett-Packard. Kahan sugirió que Intel use el punto flotante de VAX de Digital Equipment Corporation (DEC). El primer VAX, el VAX-11/780, acababa de salir a finales de 1977 y su punto flotante era muy apreciado. Sin embargo, al tratar de comercializar su chip en el mercado más amplio posible, Intel quería el mejor punto flotante posible, y Kahan pasó a redactar las especificaciones. Kahan inicialmente recomendó que la base de coma flotante fuera decimal, pero el diseño de hardware del coprocesador estaba demasiado avanzado para hacer ese cambio.
El trabajo dentro de Intel preocupó a otros proveedores, quienes establecieron un esfuerzo de estandarización para garantizar un "campo de juego nivelado". Kahan asistió a la segunda reunión del grupo de trabajo de estándares IEEE 754, celebrada en noviembre de 1977. Posteriormente, recibió permiso de Intel para presentar un borrador de propuesta basado en su trabajo para su coprocesador; se le permitió explicar los detalles del formato y su fundamento, pero nada relacionado con la arquitectura de implementación de Intel. El borrador fue coescrito con Jerome Coonen y Harold Stone, e inicialmente se conoció como la "propuesta de Kahan-Coonen-Stone" o "formato K-C-S".
Como un exponente de 8 bits no era lo suficientemente ancho para algunas operaciones deseadas para números de doble precisión, p. para almacenar el producto de dos números de 32 bits, tanto la propuesta de Kahan como una contrapropuesta de DEC utilizaron 11 bits, como el formato de punto flotante de 60 bits probado en el tiempo del CDC 6600 de 1965. Kahan& La propuesta de #39 también proporcionó infinitos, que son útiles cuando se trata de condiciones de división por cero; valores no numéricos, que son útiles cuando se trata de operaciones no válidas; números anormales, que ayudan a mitigar los problemas causados por el desbordamiento; y un sesgo de exponente mejor equilibrado, que puede ayudar a evitar el desbordamiento y el subdesbordamiento al tomar el recíproco de un número.
Incluso antes de que se aprobara, varios fabricantes habían implementado el borrador del estándar. El Intel 8087, que se anunció en 1980, fue el primer chip en implementar el borrador del estándar.
En 1980, ya se lanzó el chip Intel 8087, pero DEC siguió oponiéndose, en particular a los números anormales, debido a problemas de rendimiento y porque le daría a DEC una ventaja competitiva para estandarizar el formato de DEC.
Los argumentos sobre el desbordamiento gradual duraron hasta 1981, cuando un experto contratado por DEC para evaluarlo se puso del lado de los disidentes. DEC hizo realizar el estudio para demostrar que el subdesbordamiento gradual era una mala idea, pero el estudio concluyó lo contrario y DEC cedió. En 1985, el estándar fue ratificado, pero ya se había convertido en el estándar de facto un año antes, implementado por muchos fabricantes.
Contenido relacionado
Transacciones de Yakarta
Marco de distribucion principal
Cifrar



