Idiota (física)

En física, sacudida o sacudida es la velocidad a la que cambia la aceleración de un objeto con respecto al tiempo. Es una cantidad vectorial (que tiene tanto magnitud como dirección). Jerk se denota más comúnmente con el símbolo j y se expresa en m/s³ (unidades SI) o gravedades estándar por segundo (g₀/s).

Expresiones

Como vector, el tirón j se puede expresar como la primera derivada temporal de la aceleración, la segunda derivada temporal de la velocidad y la tercera derivada temporal de posición:

j()t)=da()t)dt=d2v()t)dt2=d3r()t)dt3{displaystyle mathbf {j} (t)={frac {mathrm {d} mathbf {a} (t)}{mathrm {d} {fnK} {fnK}} {fn}} {f}} {fn}}} {m}}}= {m}}} {m} {fn}} {} {}}}m} {}}} {}} {}}}} {}}}} {}}}}}} {}}}}}} {}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}

dónde

• a es aceleración
• v es velocidad
• r posición
• t es tiempo

Ecuaciones diferenciales de tercer orden de la forma

J()x...,x.. ,xÍ Í ,x)=0{displaystyle Jleft {fnMitbf} {fnMitbf} {x},{ddot {x}},{dot {x}},xright)=0}

Efectos fisiológicos y percepción humana

La posición del cuerpo humano se controla equilibrando las fuerzas de los músculos antagónicos. Al equilibrar una fuerza dada, como sostener un peso, la circunvolución poscentral establece un circuito de control para lograr el equilibrio deseado. Si la fuerza cambia demasiado rápido, los músculos no pueden relajarse o tensarse lo suficientemente rápido y se exceden en cualquier dirección, causando una pérdida temporal de control. El tiempo de reacción para responder a los cambios de fuerza depende de las limitaciones fisiológicas y del nivel de atención del cerebro: un cambio esperado se estabilizará más rápido que una disminución o aumento repentino de carga.

Para evitar que los pasajeros del vehículo pierdan el control sobre el movimiento del cuerpo y se lesionen, es necesario limitar la exposición tanto a la fuerza máxima (aceleración) como al tirón máximo, ya que se necesita tiempo para ajustar la tensión muscular y adaptarse incluso a cambios de estrés limitados. Los cambios repentinos en la aceleración pueden causar lesiones como latigazo cervical. Una sacudida excesiva también puede provocar una conducción incómoda, incluso a niveles que no causen lesiones. Los ingenieros dedican un esfuerzo de diseño considerable a minimizar el "movimiento brusco" en ascensores, tranvías y otros medios de transporte.

Por ejemplo, considere los efectos de la aceleración y las sacudidas cuando viaja en automóvil:

• Los controladores con habilidades y experiencia pueden acelerarse sin problemas, pero los principiantes a menudo proporcionan un gilipollas paseo. Al cambiar los engranajes en un coche con un embrague operado a pie, la fuerza de aceleración está limitada por la potencia del motor, pero un conductor inexperto puede causar un tirón severo debido al cierre intermitente de la fuerza sobre el embrague.
• La sensación de ser presionado en los asientos en un coche deportivo de alta potencia se debe a la aceleración. A medida que el coche se lanza desde el descanso, hay un gran imbécil positivo a medida que su aceleración aumenta rápidamente. Después del lanzamiento, hay un pequeño y sostenido imbécil negativo a medida que la fuerza de resistencia al aire aumenta con la velocidad del coche, disminuyendo gradualmente la aceleración y reduciendo la fuerza presionando al pasajero en el asiento. Cuando el coche alcanza su velocidad máxima, la aceleración ha alcanzado 0 y sigue siendo constante, después de lo cual no hay ningún idiota hasta que el conductor desacelera o cambia la dirección.
• Cuando se frena repentinamente o durante colisiones, los pasajeros avanzan con una aceleración inicial que es mayor que durante el resto del proceso de frenado porque la tensión muscular recupera el control del cuerpo rápidamente después del inicio del frenado o el impacto. Estos efectos no se modelan en las pruebas de vehículos porque los cadáveres y las dummies de prueba de choque no tienen control muscular activo.
• Para minimizar los efectos de un tirón, las curvas a lo largo de las carreteras están diseñadas para ser telas como son curvas ferroviarias y los lazos de montaña rusa.

Fuerza, aceleración y tirones

Para una masa constante m, la aceleración a es directamente proporcional a la fuerza F según la segunda ley del movimiento de Newton:

F=ma{displaystyle mathbf {F} =mmathbf {a}

En la mecánica clásica de cuerpos rígidos, no existen fuerzas asociadas a las derivadas de la aceleración; sin embargo, los sistemas físicos experimentan oscilaciones y deformaciones como resultado de sacudidas. Al diseñar el Telescopio Espacial Hubble, la NASA estableció límites tanto para las sacudidas como para los rebotes.

La fuerza de Abraham-Lorentz es la fuerza de retroceso sobre una partícula cargada en aceleración que emite radiación. Esta fuerza es proporcional al tirón de la partícula y al cuadrado de su carga. La teoría del absorbedor de Wheeler-Feynman es una teoría más avanzada, aplicable en un entorno cuántico y relativista, y que explica la energía propia.

En un entorno idealizado

Las discontinuidades en la aceleración no ocurren en entornos del mundo real debido a la deformación, los efectos de la mecánica cuántica y otras causas. Sin embargo, una discontinuidad de salto en la aceleración y, en consecuencia, un tirón ilimitado son factibles en un entorno idealizado, como una masa puntual idealizada que se mueve a lo largo de una trayectoria continua completa y suave por partes. La discontinuidad de salto ocurre en puntos donde el camino no es uniforme. Extrapolando de estos escenarios idealizados, uno puede describir, explicar y predecir cualitativamente los efectos del jerk en situaciones reales.

La discontinuidad de salto en la aceleración se puede modelar usando una función delta de Dirac en jerk, escalada a la altura del salto. La integración de sacudidas en el tiempo a través del delta de Dirac produce la discontinuidad de salto.

Por ejemplo, considere un camino a lo largo de un arco de radio r, que se conecta tangencialmente a una línea recta. Todo el camino es continuo, y sus piezas son suaves. Ahora suponga que una partícula puntual se mueve con velocidad constante a lo largo de este camino, por lo que su aceleración tangencial es cero. La aceleración centrípeta dada por v²/r es normal al arco y hacia adentro. Cuando la partícula pasa por la conexión de las piezas, experimenta un salto discontinuo en la aceleración dada por v²/r , y sufre un tirón que puede ser modelado por un delta de Dirac, escalado a la discontinuidad de salto.

Para un ejemplo más tangible de aceleración discontinua, considere un sistema resorte-masa ideal con la masa oscilando sobre una superficie idealizada con fricción. La fuerza sobre la masa es igual a la suma vectorial de la fuerza del resorte y la fuerza de fricción cinética. Cuando la velocidad cambia de signo (en los desplazamientos máximo y mínimo), la magnitud de la fuerza sobre la masa cambia en el doble de la magnitud de la fuerza de fricción, porque la fuerza del resorte es continua y la fuerza de fricción invierte la dirección con la velocidad. El salto en la aceleración es igual a la fuerza sobre la masa dividida por la masa. Es decir, cada vez que la masa pasa por un desplazamiento mínimo o máximo, la masa experimenta una aceleración discontinua y la sacudida contiene un delta de Dirac hasta que la masa se detiene. La fuerza de fricción estática se adapta a la fuerza residual del resorte, estableciendo un equilibrio con fuerza neta cero y velocidad cero.

Considere el ejemplo de un automóvil que frena y desacelera. Las pastillas de freno generan fuerzas de fricción cinética y pares de frenado constantes en los discos (o tambores) de las ruedas. La velocidad de rotación disminuye linealmente hasta cero con una desaceleración angular constante. La fuerza de fricción, el par y la desaceleración del automóvil repentinamente llegan a cero, lo que indica un delta de Dirac en una sacudida física. El delta de Dirac es suavizado por el entorno real, cuyos efectos acumulativos son análogos a la amortiguación de la sacudida percibida fisiológicamente. Este ejemplo ignora los efectos del deslizamiento de los neumáticos, el hundimiento de la suspensión, la desviación real de todos los mecanismos idealmente rígidos, etc.

Otro ejemplo de sacudida significativa, similar al primer ejemplo, es el corte de una cuerda con una partícula en su extremo. Suponga que la partícula oscila en una trayectoria circular con una aceleración centrípeta distinta de cero. Cuando se corta la cuerda, el camino de la partícula cambia abruptamente a un camino recto, y la fuerza en la dirección hacia adentro cambia repentinamente a cero. Imagine una fibra monomolecular cortada por un láser; la partícula experimentaría tasas muy altas de sacudidas debido al tiempo de corte extremadamente corto.

En rotación

Animation showing a four-position external Geneva drive in operation

Diagrama de fijación sobre una revolución para ángulo, velocidad angular, aceleración angular y tirón angular

Considere un cuerpo rígido que gira sobre un eje fijo en un marco de referencia inercial. Si su posición angular en función del tiempo es θ(t), la velocidad angular, la aceleración y el tirón pueden expresarse como sigue:

• Velocidad angular, ⋅ ⋅ ()t)=Silencio Silencio Í Í ()t)=dSilencio Silencio ()t)dt{displaystyle omega (t)={dot {theta }(t)={frac {mathrm {d} theta (t)}{mathrm {d} }, es el derivado del tiempo Silencio()t).
• Aceleración angular, α α ()t)=⋅ ⋅ Í Í ()t)=d⋅ ⋅ ()t)dt{displaystyle alpha (t)={dot {omega }}(t)={frac {mathrm {d}omega (t)}{mathrm {d} {} {} {}} {}}} {}} {}}}} {m}}} {}}}}} {m}}}}} {}}} }, es el derivado del tiempo ⋅()t).
• Zorro anular, Especificaciones Especificaciones ()t)=α α Í Í ()t)=⋅ ⋅ .. ()t)=Silencio Silencio ...()t){displaystyle zeta (t)={dot {alpha }(t)={ddot {omega }(t)={overset {}{theta }(t)} {} {} {fnunci)}, es el derivado del tiempo α()t).

La aceleración angular es igual al par que actúa sobre el cuerpo, dividido por el momento de inercia del cuerpo con respecto al eje de rotación momentáneo. Un cambio en el par da como resultado una sacudida angular.

El caso general de un cuerpo rígido giratorio se puede modelar utilizando la teoría del tornillo cinemático, que incluye un vector axial, la velocidad angular Ω(t), y un vector polar, velocidad lineal v(t). A partir de esto, la aceleración angular se define como

α α ()t)=ddtΩ Ω ()t)=Ω Ω Í Í ()t){displaystyle {boldsymbol {alpha } {frac {mathrm {}{mathrm {d} t}{boldsymbol {Omega } {t)={dot {boldsymbol {Omega }} {}} {} t}} {}} {f}}} {f}}}} {f}}}}}} {f}}}}} {f}}}}}}}}}} {f}}}}}}}} {f}}}}} {f}}}} {f}}}}}}}}}} {f}}}}} {f}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

y el tirón angular viene dado por

Especificaciones Especificaciones ()t)=ddtα α ()t)=α α Í Í ()t)=Ω Ω .. ()t){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrom {} {m} {m} t} {m} {fnuncio} {fnMicrosoft} {fnMicrosoft Sans} {fnMicrosoft Sans Serif} {fnMicros} {fnMicrosoft}}} {f}}}}}}}}}} {f}f}}}}fnMisigual}fnMinMicrom} {f}fnMinMinun}fnMinMinMinun}fnMinun}fnMinMinun}fnMinun}fnun}fnunt}fnun}fnun}fnun}fnMinunt} {fnMinMinMinun}fnMinMinMinMinun}f}fnMin

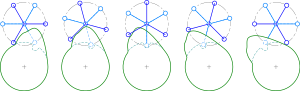
Por ejemplo, considere una unidad de Ginebra, un dispositivo utilizado para crear una rotación intermitente de una rueda motriz (la rueda azul en la animación) mediante la rotación continua de una rueda motriz (la rueda roja en la animación). Durante un ciclo de la rueda motriz, la posición angular de la rueda motriz θ cambia 90 grados y luego permanece constante. Debido al grosor finito de la horquilla de la rueda motriz (la ranura para el pasador de conducción), este dispositivo genera una discontinuidad en la aceleración angular α, y un tirón angular ilimitado ζ en la rueda motriz.

Jerk no impide que la unidad Geneva se utilice en aplicaciones como proyectores de películas y cámaras. En los proyectores de películas, la película avanza fotograma a fotograma, pero el funcionamiento del proyector tiene poco ruido y es muy fiable debido a la baja carga de película (sólo se impulsa una pequeña sección de película que pesa unos pocos gramos), la velocidad moderada (2,4 m/s), y la baja fricción.

Dobles unidades de cámara

1/6 por revolución

1/3 por revolución

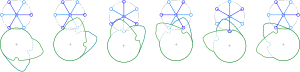
Con los sistemas de accionamiento por leva, el uso de una leva doble puede evitar las sacudidas de una sola leva; sin embargo, la doble cámara es más voluminosa y costosa. El sistema de doble leva tiene dos levas en un eje que desplaza un segundo eje en una fracción de revolución. El gráfico muestra transmisiones escalonadas de un sexto y un tercio de rotación por una revolución del eje motriz. No hay juego radial porque dos brazos de la rueda escalonada siempre están en contacto con la doble leva. En general, se pueden usar contactos combinados para evitar las sacudidas (y el desgaste y el ruido) asociados con un solo seguidor (como un solo seguidor que se desliza a lo largo de una ranura y cambiar su punto de contacto de un lado de la ranura al otro se puede evitar usando dos seguidores deslizándose a lo largo de la misma ranura, un lado cada uno).

En materia elásticamente deformable

Patrones de onda de compresión

Ola de avión

Simetría cilíndrica

Una masa elásticamente deformable se deforma bajo una fuerza aplicada (o aceleración); la deformación es función de su rigidez y de la magnitud de la fuerza. Si el cambio de fuerza es lento, la sacudida es pequeña y la propagación de la deformación se considera instantánea en comparación con el cambio de aceleración. El cuerpo distorsionado actúa como si estuviera en un régimen cuasiestático, y solo una fuerza cambiante (sacudida distinta de cero) puede causar la propagación de ondas mecánicas (u ondas electromagnéticas para una partícula cargada); por lo tanto, para sacudidas distintas de cero a altas, se debe considerar una onda de choque y su propagación a través del cuerpo.

La propagación de la deformación se muestra en el gráfico "Patrones de ondas de compresión" como una onda plana de compresión a través de un material elásticamente deformable. También se muestran, para el tirón angular, las ondas de deformación que se propagan en un patrón circular, lo que provoca un esfuerzo cortante y posiblemente otros modos de vibración. El reflejo de las ondas a lo largo de los límites genera patrones de interferencia constructivos (no ilustrados), que producen tensiones que pueden exceder los límites del material. Las ondas de deformación pueden causar vibraciones, que pueden provocar ruido, desgaste y fallas, especialmente en casos de resonancia.

Polo con top masivo

El gráfico con la leyenda "Polo con parte superior masiva" muestra un bloque conectado a un poste elástico y una parte superior maciza. El poste se dobla cuando el bloque acelera, y cuando la aceleración se detiene, la parte superior oscilará (amortiguada) bajo el régimen de rigidez del poste. Se podría argumentar que una mayor sacudida (periódica) podría excitar una mayor amplitud de oscilación porque las pequeñas oscilaciones son amortiguadas antes del refuerzo por una onda de choque. También se puede argumentar que una sacudida más grande podría aumentar la probabilidad de excitar un modo resonante porque los componentes de onda más grandes de la onda de choque tienen frecuencias y coeficientes de Fourier más altos.

Perfil de aceleración sinusoidal

Para reducir la amplitud de las ondas de tensión excitadas y las vibraciones, se puede limitar la sacudida dando forma al movimiento y haciendo que la aceleración sea continua con pendientes lo más planas posible. Debido a las limitaciones de los modelos abstractos, los algoritmos para reducir las vibraciones incluyen derivadas más altas, como rebotes, o sugieren regímenes continuos tanto para aceleración como para sacudidas. Un concepto para limitar el tirón es dar forma sinusoidal a la aceleración y la desaceleración con una aceleración cero en el medio (consulte el gráfico titulado "Perfil de aceleración sinusoidal"), haciendo que la velocidad parezca sinusoidal con una velocidad máxima constante. El tirón, sin embargo, permanecerá discontinuo en los puntos donde la aceleración entra y sale de las fases cero.

En el diseño geométrico de caminos y vías

Una curva de transición de pista limita el tirón. La transición se muestra en rojo entre la línea recta azul y el arco verde.

Las carreteras y vías están diseñadas para limitar las sacudidas causadas por los cambios en su curvatura. En los ferrocarriles, los diseñadores utilizan 0,35 m/s³ como objetivo de diseño y 0,5 m/s³ como máximo. Las curvas de transición de pista limitan el tirón cuando se pasa de una línea recta a una curva, o viceversa. Recuerde que en un movimiento de velocidad constante a lo largo de un arco, el tirón es cero en la dirección tangencial y distinto de cero en la dirección normal hacia adentro. Las curvas de transición aumentan gradualmente la curvatura y, en consecuencia, la aceleración centrípeta.

Una espiral de Euler, la curva de transición teóricamente óptima, aumenta linealmente la aceleración centrípeta y da como resultado una sacudida constante (ver gráfico). En aplicaciones del mundo real, el plano de la pista está inclinado (peralte) a lo largo de las secciones curvas. La pendiente provoca una aceleración vertical, que es una consideración de diseño para el desgaste de la vía y el terraplén. La Wiener Kurve (curva vienesa) es una curva patentada diseñada para minimizar este desgaste.

Las montañas rusas también están diseñadas con transiciones de pista para limitar las sacudidas. Al entrar en un bucle, los valores de aceleración pueden alcanzar alrededor de 4g (40 m/s²), y circular en este entorno de alta aceleración solo es posible con transiciones de pista. Las curvas en forma de S, como la figura de ocho, también usan transiciones de pista para paseos suaves.

En control de movimiento

En el control de movimiento, el diseño se centra en el movimiento recto y lineal, con la necesidad de mover un sistema de una posición estable a otra (movimiento de punto a punto). La preocupación del diseño desde la perspectiva del tirón es el tirón vertical; el tirón de la aceleración tangencial es efectivamente cero ya que el movimiento lineal no es rotacional.

Las aplicaciones de control de movimiento incluyen ascensores de pasajeros y herramientas de mecanizado. Limitar el tirón vertical se considera esencial para la comodidad de uso del ascensor. ISO 18738 especifica los métodos de medición de la calidad de conducción del ascensor con respecto a las sacudidas, la aceleración, la vibración y el ruido; sin embargo, el estándar especifica niveles de calidad de conducción aceptable o inaceptable. Se informa que la mayoría de los pasajeros califican una sacudida vertical de 2 m/s³ como aceptable y 6 m/s³ como intolerable. Para hospitales, 0,7 m/s³ es el límite recomendado.

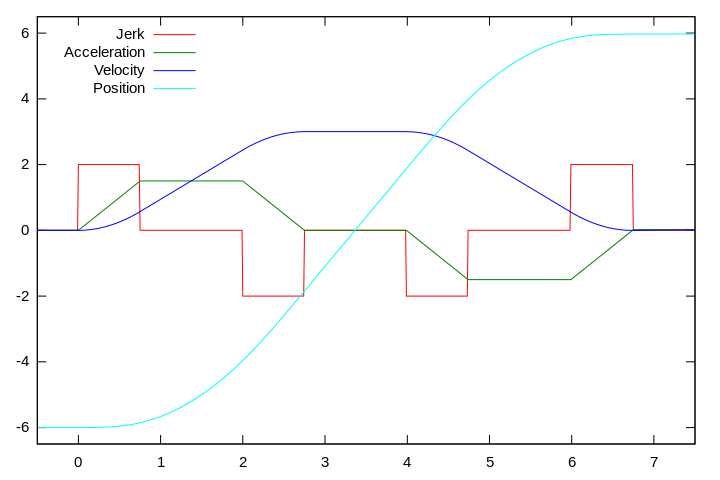
Un objetivo de diseño principal para el control de movimiento es minimizar el tiempo de transición sin exceder los límites de velocidad, aceleración o tirones. Considere un perfil de control de movimiento de tercer orden con fases de aceleración y desaceleración cuadráticas en la velocidad (consulte la figura).

Este perfil de movimiento consta de los siguientes siete segmentos:

1. La aceleración se acumula — límite positivo del tirón; aumento lineal de la aceleración al límite de aceleración positivo; aumento cuadrático de la velocidad
2. Límite de aceleración superior — cero tirón; aumento lineal de velocidad
3. Aceleración de la rampa hacia abajo — límite negativo del tirón; disminución lineal de la aceleración; (negativo) aumento cuadrático de la velocidad, acercando el límite de velocidad deseado
4. Límite de velocidad — cero tirón; aceleración cero
5. La desaceleración se acumula — límite negativo del tirón; disminución lineal de la aceleración al límite de aceleración negativo; (negativo) disminución cuadrática de la velocidad
6. Límite de desaceleración inferior — cero tirón; disminución lineal de velocidad
7. Desceleración de la rampa hacia abajo — límite positivo del tirón; aumento lineal de aceleración a cero; disminución cuadrática de la velocidad; aproximación de la posición deseada a velocidad cero y aceleración cero

El período de tiempo del segmento cuatro (velocidad constante) varía con la distancia entre las dos posiciones. Si esta distancia es tan pequeña que la omisión del segmento cuatro no sería suficiente, entonces los segmentos dos y seis (aceleración constante) podrían reducirse igualmente y no se alcanzaría el límite de velocidad constante. Si esta modificación no reduce suficientemente la distancia recorrida, entonces los segmentos uno, tres, cinco y siete podrían acortarse en la misma cantidad y no se alcanzarían los límites de aceleración constante.

Se utilizan otras estrategias de perfil de movimiento, como minimizar el cuadrado de la sacudida para un tiempo de transición dado y, como se mencionó anteriormente, perfiles de aceleración de forma sinusoidal. Los perfiles de movimiento se adaptan a aplicaciones específicas, incluidas máquinas, transportadores de personas, polipastos de cadena, automóviles y robótica.

En fabricación

Jerk es una consideración importante en los procesos de fabricación. Los cambios rápidos en la aceleración de una herramienta de corte pueden provocar un desgaste prematuro de la herramienta y producir cortes desiguales; en consecuencia, los controladores de movimiento modernos incluyen características de limitación de tirones. En ingeniería mecánica, el tirón, además de la velocidad y la aceleración, se considera en el desarrollo de perfiles de leva debido a las implicaciones tribológicas y la capacidad del cuerpo accionado para seguir el perfil de la leva sin vibraciones. Jerk a menudo se considera cuando la vibración es una preocupación. Un dispositivo que mide el tirón se llama "medidor de tirón".

Otras derivadas

También se han nombrado otras derivadas del tiempo, como chasquido o jounce (cuarta derivada), crujido (quinta derivada) y pop (sexta derivada). Sin embargo, rara vez aparecen derivadas temporales de posición de orden superior a cuatro.

Los términos snap, crackle y pop—para las derivadas cuarta, quinta y sexta de posición—se inspiraron en el mascotas publicitarias Snap, Crackle y Pop.