Identidad (matemáticas)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Ecuación que está satisfecha para todos los valores de las variables

En matemáticas, un identidad es una igualdad relacionada con una expresión matemática Aa otra expresión matemáticaB, tal que A y B (que podría contener algunas variables) producen el mismo valor para todos los valores de las variables dentro de un cierto rango de validez. En otras palabras, A=B es una identidad si A y B definir las mismas funciones, y una identidad es una igualdad entre las funciones que se definen de manera diferente. Por ejemplo, ${displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ y ${displaystyle cos ^{2}theta +sin ^{2}theta =1}$ son identidades. Las identidades son a veces indicadas por el símbolo de la barra triple $↑$ en lugar de $=$ El signo igual. Formalmente, una identidad es una igualdad universalmente cuantificada.

Identidades comunes

Identidades algebraicas

Ciertas identidades, como ${displaystyle a+0=a}$ y ${displaystyle a+(-a)=0}$ , formar la base del álgebra, mientras que otras identidades, como ${displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ y $a^2 - b^2 = (a+b)(a-b)$ , puede ser útil para simplificar las expresiones algebraicas y expandirlas.

Identidades trigonométricas

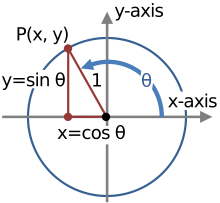
Geométricamente, las identidades trigonométricas son identidades que involucran ciertas funciones de uno o más ángulos. Son distintas de las identidades de triángulos, que son identidades que involucran tanto los ángulos como las longitudes de los lados de un triángulo. Solo los primeros están cubiertos en este artículo.

Estas identidades son útiles cuando es necesario simplificar expresiones que involucran funciones trigonométricas. Otra aplicación importante es la integración de funciones no trigonométricas: una técnica común que implica primero usar la regla de sustitución con una función trigonométrica y luego simplificar la integral resultante con una identidad trigonométrica.

Uno de los ejemplos más destacados de identidades trigonométricas implica la ecuación ${displaystyle sin ^{2}theta +cos ^{2}theta =1,}$ que es verdad para todos los valores reales de $theta$ . Por otro lado, la ecuación

{displaystyle cos theta =1}

es sólo cierto para ciertos valores $theta$ No todos. Por ejemplo, esta ecuación es verdadera cuando ${displaystyle theta =0,}$ pero falso $theta =2$ .

Otro grupo de identidades trigonométricas se refiere a las denominadas fórmulas de adición/substracción (por ejemplo, la identidad de doble ángulo ${displaystyle sin(2theta)=2sin theta cos theta }$ , la fórmula de adición para ${displaystyle tan(x+y)}$ ), que se puede utilizar para romper expresiones de ángulos más grandes en aquellos con componentes más pequeños.

Identidades exponenciales

Las siguientes identidades son válidas para todos los exponentes enteros, siempre que la base no sea cero:

{begin{aligned}b^{m+n}&=b^{m}cdot b^{n}\(b^{m})^{n}&=b^{mcdot n}\(bcdot c)^{n}&=b^{n}cdot c^{n}end{aligned}}

A diferencia de la suma y la multiplicación, la exponenciación no es conmutativa. Por ejemplo, 2 + 3 = 3 + 2 = 5 y 2 · 3 = 3 · 2 = 6, pero 2³ = 8 mientras que 3² = 9.

A diferencia de la suma y la multiplicación, la exponenciación tampoco es asociativa. Por ejemplo, (2 + 3) + 4 = 2 + (3 + 4) = 9 y (2 · 3) · 4 = 2 · (3 · 4) = 24, pero 2³ elevado al 4 es 8⁴ (o 4096) mientras que 2 elevado al 3⁴ es 2⁸¹ (o 2,417,851,639,229,258,349,412,352). Cuando no se escriben paréntesis, por convención el orden es de arriba hacia abajo, no de abajo hacia arriba:

{displaystyle b^{p^{q}}:=b^{(p^{q})},}

mientras que

{displaystyle (b^{p})^{q}=b^{pcdot q}.}

Identidades logarítmicas

Varias fórmulas importantes, a veces llamadas identidades logarítmicas o leyes logarítmicas, relacionan logaritmos entre sí:

Producto, cociente, potencia y raíz

El logaritmo de un producto es la suma de los logaritmos de los números que se multiplican; el logaritmo de la relación de dos números es la diferencia de los logaritmos. El logaritmo del $p$ el poder de un número es $p$ tiempos el logaritmo del número mismo; el logaritmo de un $p$ la raíz es el logaritmo del número dividido por $p$ . En el cuadro siguiente se enumeran estas identidades con ejemplos. Cada una de las identidades puede derivarse después de la sustitución de las definiciones de logaritmo ${displaystyle x=b^{log _{b}x},}$ y/o ${displaystyle y=b^{log _{b}y},}$ en los lados izquierdos.

	Formula	Ejemplo
producto	${displaystyle log _{b}(xy)=log _{b}(x)+log _{b}(y)}$	${displaystyle log _{3}(243)=log _{3}(9cdot 27)=log _{3}(9)+log _{3}(27)=2+3=5}$
quotient	${displaystyle log _{b}!left({frac {x}{y}}right)=log _{b}(x)-log _{b}(y)}$	${displaystyle log _{2}(16)=log _{2}!left({frac {64}{4}}right)=log _{2}(64)-log _{2}(4)=6-2=4}$
poder	${displaystyle log _{b}(x^{p})=plog _{b}(x)}$	${displaystyle log _{2}(64)=log _{2}(2^{6})=6log _{2}(2)=6}$
root	${displaystyle log _{b}!{sqrt[{p}]{x}}={frac {log _{b}(x)}{p}}}$	${displaystyle log _{10}!{sqrt {1000}}={frac {1}{2}}log _{10}1000={frac {3}{2}}=1.5}$

Cambio de base

El logaritmo log_b(x) se puede calcular a partir de los logaritmos de x y b con respecto a una base arbitraria k utilizando la siguiente fórmula:

{displaystyle log _{b}(x)={frac {log _{k}(x)}{log _{k}(b)}}.}

Las calculadoras científicas típicas calculan los logaritmos en base 10 y e. Los logaritmos con respecto a cualquier base b se pueden determinar utilizando cualquiera de estos dos logaritmos mediante la fórmula anterior:

{displaystyle log _{b}(x)={frac {log _{10}(x)}{log _{10}(b)}}={frac {log _{e}(x)}{log _{e}(b)}}.}

Dado un número x y su logaritmo log_b(x) en una base desconocida b, la base viene dada por:

b=x^{frac {1}{log _{b}(x)}}.

Identidades de funciones hiperbólicas

Las funciones hiperbólicas satisfacen muchas identidades, todas ellas similares en forma a las identidades trigonométricas. De hecho, la regla de Osborn establece que uno puede convertir cualquier identidad trigonométrica en una identidad hiperbólica expandiéndola completamente en términos de potencias enteras de senos y cosenos, cambiando seno a senh y coseno a cosh, y cambiando el signo de todo término que contenga un producto de un número par de senos hiperbólicos.

La función de Gudermann da una relación directa entre las funciones trigonométricas y las hiperbólicas que no involucra números complejos.

Lógica y álgebra universal

Formally, una identidad es una verdadera fórmula universalmente cuantificada de la forma ${displaystyle forall x_{1},ldotsx_{n}:s=t,}$ Donde $s$ y $t$ son términos sin otras variables libres que ${displaystyle x_{1},ldotsx_{n}.}$ El prefijo cuantificador ${displaystyle forall x_{1},ldotsx_{n}}$ a menudo se deja implícita, cuando se dice que la fórmula es una identidad. Por ejemplo, los axiomas de un monoide a menudo se dan como fórmulas

{displaystyle forall x,y,z:x*(y*z)=(x*y)*z,quad forall x:x*1=x,quad forall x:1*x=x,}

o, en breve,

{displaystyle x*(y*z)=(x*y)*z,qquad x*1=x,qquad 1*x=x.}

Entonces, estas fórmulas son identidades en cada monoide. Como para cualquier igualdad, las fórmulas sin cuantificador suelen llamarse ecuaciones. En otras palabras, una identidad es una ecuación que se cumple para todos los valores de las variables.

Contenido relacionado

Más resultados...