Icoságono

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Poligono con 20 bordes

Did you mean:

In geometry, a icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon 's interior angles is 3240 degrees.

Icoságono regular

El icoságono regular tiene el símbolo de Schläfli ${20}$ y también se puede construir como un decágono truncado, $t{10}$ , o un pentágono truncado dos veces, $tt{5}$ .

Un ángulo interior en un icoságono regular es de 162°, lo que significa que un ángulo exterior sería de 18°.

El área de un icoságono regular con una longitud de arista $t$ es

A={5}t^2(1+sqrt{5}+sqrt{5+2sqrt{5}}) simeq 31.5687 t^2.

Did you mean:

In terms of the radius Ri> of its circumcircle, the area is

$A=frac{5R^2}{2}(sqrt{5}-1);$

ya que el área del círculo es $pi R^{2},$ el icosagon regular llena aproximadamente el 98.36% de su círculo.

Usos

Showing translation for
The Big Wheel on the popular US game show The Price Is Right has an octagonal cross-section.
Did you mean:
The Globe, the outdoor theater used by William Shakespeare 's acting company, was discovered to have been built on an octagonal foundation when a partial excavation was done in 1989.
Did you mean:
As a polygonal path, the swastika is considered to be an irregular icosagon.
Un cuadrado regular, pentágono y icosagon puede llenar completamente un vértice plano.
Construcción
Como $20 = 2 2 \times 5$ , el icoságono regular se puede construir usando un compás y una regla, o mediante la bisección de un decágono regular., o un pentágono regular dos veces bisectado:

Construcción de un icosagon regular
Construcción de un decagón regular
La proporción áurea en un icoságono
En la construcción con longitud lateral dada el arco circular alrededor $C$ con radio $CD$ , comparte el segmento $E 20 F$ en relación de la relación de oro.
${displaystyle {frac {overline {E_{20}E_{1}}}{overline {E_{1}F}}}={frac {overline {E_{20}F}}{overline {E_{20}E_{1}}}}={frac {1+{sqrt {5}}}{2}}=varphi approx 1.618}$
Icosagon con longitud lateral dada, animación (La construcción es muy similar a la de decagón con longitud lateral dada)
Simetría
Simetrías de un icosagon regular. Los vértices son coloreados por sus posiciones de simetría. Los espejos azules se dibujan a través de vértices, y los espejos púrpuras se dibujan a través del borde. Las órdenes de giro se dan en el centro.
El icoságono regular tiene simetría Dih20, orden 40. Hay 5 simetrías diédricas de subgrupo: $(Dih 10, Dih 5)$ y $(Dih 4, Dih 2 y Dih 1)$ , y 6 simetrías de grupos cíclicos: $(Z 20, Z 10, Z 5)$ , y ( $Z 4, Z 2, Z 1)$ .
Estas 10 simetrías se pueden ver en 16 simetrías distintas en el icoságono, un número mayor porque las líneas de reflexión pueden pasar a través de vértices o aristas. John Conway los etiqueta mediante letras y orden de grupo. La simetría completa de la forma regular es $r40$ y ninguna simetría está etiquetada como $a1 . Las simetrías diédricas se dividen dependiendo de si pasan por vértices (d para diagonal) o por aristas (p para perpendiculares) y i cuando las líneas de reflexión atraviesan ambos bordes y vértices. Las simetrías cíclicas en la columna del medio están etiquetadas como g por sus órdenes de giro central.$
Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Sólo el subgrupo $g20$ no tiene grados de libertad pero puede verse como aristas dirigidas.
Los icoságonos irregulares de mayor simetría son $d20$ , un icoságono isogonal construido por diez espejos que pueden alternar bordes largos y cortos, y $p20$ , un icoságono isotoxal, construido con longitudes de bordes iguales, pero vértices que alternan dos ángulos internos diferentes. Estas dos formas son duales entre sí y tienen la mitad del orden de simetría del icoságono regular.
Disección
20-gon con 180 rombs

ordinario
Isotoxal
Coxeter afirma que cada zonogon (un góno $2 m$ cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en $m (m -1)/2$ paralelogramos. En particular, esto es cierto para los polígonos regulares con el mismo número de lados, en cuyo caso todos los paralelogramos son rombos. Para el icoságono, $m =10$ , y se puede dividir en 45: 5 cuadrados y 4 conjuntos de 10 rombos. Esta descomposición se basa en una proyección de polígono de Petrie de un cubo de 10, con 45 de 11520 caras. La lista OEIS: A006245 enumera el número de soluciones como 18,410,581,880, incluidas rotaciones de hasta 20 veces y formas quirales en reflexión.
Disección en 45 rombs

10-cube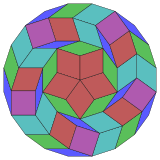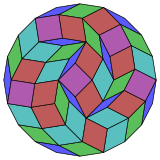
Polígonos relacionados
Un icosagrama es un polígono estrella de 20 lados, representado por el símbolo ${20/n}$ . Hay tres formas regulares dadas por los símbolos de Schläfli: ${20/3}$ , ${20/7}$ y ${20/9}$ . También hay cinco figuras de estrellas regulares (compuestas) que utilizan la misma disposición de vértices: $2{10}$ , $4{5}$ , $5{4}$ , $2{10/3}$ , $4{5/2}$ y $10{2}$ .
n 1 2 3 4 5
Formulario Convex polygon Compuesto Pológono estrella Compuesto
Imagen
{20/1} = {20}
{20/2} = 2{10}
{20/3}
{20/4} = 4{5}
{20/5} = 5{4}
Ángulo interior 162° 144° 126° 108° 90°
n 6 7 8 9 10
Formulario Compuesto Pológono estrella Compuesto Pológono estrella Compuesto
Imagen
{20/6} = 2{10/3}
{20/7}
{20/8} = 4{5/2}
{20/9}
{20/10} = 10{2}
Ángulo interior 72° 54° 36° 18° 0°
Los truncamientos más profundos del decágono y el decagrama regulares pueden producir formas de icosagramas intermedias isogonales (transitivas a vértices) con vértices igualmente espaciados y dos longitudes de aristas.
Un icosagrama normal, ${20/9}$ , puede verse como un decágono cuasitruncado, $t{10/9}={20 /9}$ . De manera similar, un decagramo, ${10/3}$ tiene un cuasitruncamiento $t{10/7}={20/7}$ , y finalmente, un simple truncamiento de un decagramo da $t{10/3}={20/3}$ .
Icosagrams as truncations of a regular decagons and decagrams, {10}, {10/3}
Quasiregular Quasiregular

T{10}={20}
t{10/9}={20/9}

t{10/3}={20/3}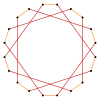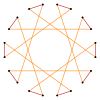
t{10/7}={20/7}
Polígonos de Petrie
El icoságono regular es el polígono de Petrie para varios politopos de dimensiones superiores, que se muestran en proyecciones ortogonales en planos de Coxeter:
A₁₉ B₁₀ D₁₁ E₈ H₄ 1⁄22H₂ 2H₂

19-simplex
10-orthoplex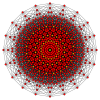
10-cube
11-demicube
(421)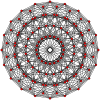
600 celdas
Gran antiprisma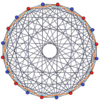
10-10 duopyramid
10-10 duoprismo
También es el polígono de Petrie para el icosaédrico de 120 celdas, el pequeño estrellado de 120 celdas, el gran icosaédrico de 120 celdas y el bisabuelo de 120 celdas.

Construcción de un icosagon regular	Construcción de un decagón regular

20-gon con 180 rombs
ordinario	Isotoxal

Disección en 45 rombs
10-cube

n	1	2	3	4	5
Formulario	Convex polygon	Compuesto	Pológono estrella	Compuesto
Imagen	{20/1} = {20}	{20/2} = 2{10}	{20/3}	{20/4} = 4{5}	{20/5} = 5{4}
Ángulo interior	162°	144°	126°	108°	90°
n	6	7	8	9	10
Formulario	Compuesto	Pológono estrella	Compuesto	Pológono estrella	Compuesto
Imagen	{20/6} = 2{10/3}	{20/7}	{20/8} = 4{5/2}	{20/9}	{20/10} = 10{2}
Ángulo interior	72°	54°	36°	18°	0°

A₁₉	B₁₀	D₁₁	E₈	H₄	1⁄22H₂	2H₂
19-simplex	10-orthoplex	10-cube	11-demicube	(421)	600 celdas	Gran antiprisma	10-10 duopyramid	10-10 duoprismo

Contenido relacionado

Mapa exponencial (geometría de Riemann)
En la geometría de Riemann, un mapa exponencial es un mapa de un subconjunto de un espacio tangente TpM de una variedad Riemanniana M a M misma. La métrica...
Punto aislado
En matemáticas, un punto x se llama punto aislado de un subconjunto S si x es un elemento de S y existe una vecindad de x que no contiene ningún otro punto...
Polígono equilátero
En geometría, un polígono equilátero es un polígono que tiene todos los lados de la misma longitud. Excepto en el caso del triángulo, un polígono...
Más resultados...
Te puede interesar

Quasiregular					Quasiregular
T{10}={20}					t{10/9}={20/9}
t{10/3}={20/3}					t{10/7}={20/7}