Homotetia

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Homothety: Ejemplo con $0}" xmlns="http://www.w3.org/1998/Math/MathML">k■0{displaystyle k]0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27b3af208b148139eefc03f0f80fa94c38c5af45" style="vertical-align: -0.338ex; width:5.472ex; height:2.176ex;"/>$
Para $k=1$ uno consigue el *identidad* (sin punto se mueve),
para $1}" xmlns="http://www.w3.org/1998/Math/MathML">k■1{displaystyle k]1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5cda43bd4034dc2d04cd562005d0af81d3d2dbc6" style="vertical-align: -0.338ex; width:5.472ex; height:2.176ex;"/>$ an *ampliación*
para $<math alttext="{displaystyle kk.1{displaystyle k won1} <img alt="{displaystyle k$ a *Reducción*

Ejemplo con $<math alttext="{displaystyle kk.0{displaystyle k made0} <img alt="k$
Para $k=-1$ uno consigue un punto de reflexión en el punto $S$

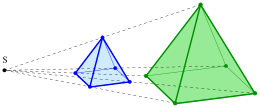
En matemáticas, a homothety (o homothecy, o dilatación homogénea) es una transformación de un espacio afinado determinado por un punto S llamada centro y un número no cero $k$ llamada ratio, que envía punto $X$ a un punto $X'$ por la regla

{displaystyle {overrightarrow {SX'}}=k{overrightarrow {SX}}}

para un número fijo

{displaystyle kneq 0}

Usando vectores de posición:

{displaystyle mathbf {x} '=mathbf {s} +k(mathbf {x} -mathbf {s})}

En caso de ${displaystyle S=O}$ (Origin):

{displaystyle mathbf {x} '=kmathbf {x} }

que es un escalado uniforme y muestra el significado de opciones especiales para $k$ :

para

k=1

uno consigue el identidad mapeo,

para

k=-1

uno consigue el reflexión en el centro,

Para $1/k$ uno consigue el inverso cartografía definida por $k$ .

En las homotheties de la geometría euclidiana son las similitudes que fijan un punto y o bien conservan (si $0}" xmlns="http://www.w3.org/1998/Math/MathML">k■0{displaystyle k]0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27b3af208b148139eefc03f0f80fa94c38c5af45" style="vertical-align: -0.338ex; width:5.472ex; height:2.176ex;"/>$ ) o inverso (si $<math alttext="{displaystyle kk.0{displaystyle k made0} <img alt="k$ ) la dirección de todos los vectores. Junto con las traducciones, todas las homotheties de un espacio affine (o Euclidean) forman un grupo, el grupo de dilaciones o homothety-translations. Estas son precisamente las transformaciones afinadas con la propiedad que la imagen de cada línea g es una línea paralela a g.

En geometría proyectiva, una transformación homotética es una transformación de similitud (es decir, fija una involución elíptica dada) que deja la línea en el infinito invariante puntualmente.

En la geometría euclidiana, una homoteca de relación $k$ multiplicaciones distancias entre puntos por ${displaystyle |k|}$ , áreas por $k^2$ y volúmenes por ${displaystyle |k|^{3}}$ . Aquí. $k$ es ratio de aumento o factor de dilación o factor de escala o relación de similitud. Tal transformación se puede llamar ampliación si el factor de escala excede 1. El punto fijo mencionado S se llama Centro homotético o centro de similitud o centro de similitud.

El término, acuñado por el matemático francés Michel Chasles, se deriva de dos elementos griegos: el prefijo homo- (όμο), que significa "similar", y tesis (Θέσις), que significa "posición". Describe la relación entre dos figuras de la misma forma y orientación. Por ejemplo, dos muñecas rusas que miran en la misma dirección pueden considerarse homotéticas.

Las homotetas se utilizan para escalar el contenido de las pantallas de las computadoras; por ejemplo, teléfonos inteligentes, portátiles y portátiles.

Propiedades

Las siguientes propiedades son válidas en cualquier dimensión.

Mapeo de líneas, segmentos de línea y ángulos

Una homotecia tiene las siguientes propiedades:

A línea se mapea en una línea paralela. Por lo tanto: ángulos permanecer sin cambios.
El ratio de dos segmentos de línea se conserva.

Ambas propiedades muestran:

Una homoteca es una similaridad.

Derivación de las propiedades:Para hacer los cálculos fácil se supone que el centro $S$ es el origen: ${displaystyle mathbf {x} to kmathbf {x} }$ . Una línea $g$ con representación paramétrica ${displaystyle mathbf {x} =mathbf {p} +tmathbf {v} }$ se mapea en el conjunto de puntos $g'$ con ecuación ${displaystyle mathbf {x} =k(mathbf {p} +tmathbf {v})=kmathbf {p} +tkmathbf {v} }$ , que es una línea paralela a $g$ .

La distancia de dos puntos ${displaystyle P:mathbf {p};Q:mathbf {q} }$ es ${displaystyle |mathbf {p} -mathbf {q} |}$ y ${displaystyle |kmathbf {p} -kmathbf {q} |=|k||mathbf {p} -mathbf {q} |}$ la distancia entre sus imágenes. Por lo tanto, ratio (cociente) de dos segmentos de línea sigue sin modificarse.

En caso de ${displaystyle Sneq O}$ el cálculo es análogo pero un poco extenso.

Consecuencias: Un triángulo se mapea sobre otro similar. La imagen homotética de un círculo es un círculo. La imagen de una elipse es similar. es decir, la relación de los dos ejes no cambia.

Construcciones gráficas

Usando el teorema de la intersección

Si para una homoteca con centro $S$ la imagen $Q_{1}$ de un punto $P_{1}$ se da (ver diagrama) entonces la imagen $Q_{2}$ de un segundo punto $P_{2}$ , que no está en línea ${displaystyle SP_{1}}$ se puede construir gráficamente utilizando el teorema de interceptación: $Q_{2}$ es el punto común de dos líneas $overline {P_{1}P_{2}}$ y ${displaystyle {overline {SP_{2}}}}$ . La imagen de un punto collinear con ${displaystyle P_{1},Q_{1}}$ puede determinarse utilizando ${displaystyle P_{2},Q_{2}}$ .

Utilizando un pantógrafo

Antes de que las computadoras se volvieran omnipresentes, las escalas de los dibujos se realizaban utilizando un pantógrafo, una herramienta similar a una brújula.

Did you mean: Construction and geometric background:

Toma 4 varillas y monta un móvil paralelogramo con vértices ${displaystyle P_{0},Q_{0},H,P}$ tal que las dos barras de reunión en $Q_{0}$ se prolongan en el otro extremo como se muestra en el diagrama. Elija el ratio $k$ .
En las barras prolongadas marcan los dos puntos ${displaystyle S,Q}$ tales que ${displaystyle |SQ_{0}|=k|SP_{0}|}$ y ${displaystyle |QQ_{0}|=k|HQ_{0}|}$ . Este es el caso si ${displaystyle |SQ_{0}|={tfrac {k}{k-1}}|P_{0}Q_{0}|.}$ (En lugar de $k$ la ubicación del centro $S$ se puede prescribir. En este caso la relación es ${displaystyle k=|SQ_{0}|/|SP_{0}|}$ .)
Adjuntar las varillas móviles girables en el punto $S$ .
Vary la ubicación del punto $P$ y marcar en cada momento $Q$ .

Debido a ${displaystyle |SQ_{0}|/|SP_{0}|=|Q_{0}Q|/|PP_{0}|}$ (ver diagrama) se obtiene de la interceptar que los puntos ${displaystyle S,P,Q}$ son collinear (en línea) y ecuación ${displaystyle |SQ|=k|SP|}$ sostiene. Eso muestra: el mapeo $Pto Q$ es una homoteca con centro $S$ y ratio $k$ .

Composición

La composición de dos homoteties con la mismo centro $S$ es otra vez una homoteca con el centro $S$ . Las homotheties con el centro $S$ formar un grupo.
La composición de dos homoteties con diferentes centros $S_{1},S_{2}$ y sus ratios $k_{1},k_{2}$ es

en caso de

{displaystyle k_{1}k_{2}neq 1}

a homothety con su centro en línea

{displaystyle {overline {S_{1}S_{2}}}}

y ratio

k_1k_2

en caso de

{displaystyle k_{1}k_{2}=1}

a traducción en dirección

{displaystyle {overrightarrow {S_{1}S_{2}}}}

. Especialmente, si

{displaystyle k_{1}=k_{2}=-1}

(puntos de reflexión).

Derivación:

Para la composición ${displaystyle sigma _{2}sigma _{1}}$ de las dos $sigma _{1},sigma _{2}$ con centros $S_{1},S_{2}$ con

{displaystyle sigma _{1}:mathbf {x} to mathbf {s} _{1}+k_{1}(mathbf {x} -mathbf {s} _{1}),}

{displaystyle sigma _{2}:mathbf {x} to mathbf {s} _{2}+k_{2}(mathbf {x} -mathbf {s} _{2}) }

uno consigue por cálculo para la imagen del punto ${displaystyle X:mathbf {x} }$ :

{displaystyle (sigma _{2}sigma _{1})(mathbf {x})=mathbf {s} _{2}+k_{2}{big (}mathbf {s} _{1}+k_{1}(mathbf {x} -mathbf {s} _{1})-mathbf {s} _{2}{big)}}

{displaystyle qquad qquad =(1-k_{1})k_{2}mathbf {s} _{1}+(1-k_{2})mathbf {s} _{2}+k_{1}k_{2}mathbf {x} }

Por lo tanto, la composición es

en caso de

{displaystyle k_{1}k_{2}=1}

a traducción en dirección

{displaystyle {overrightarrow {S_{1}S_{2}}}}

vector

{displaystyle (1-k_{2})(mathbf {s} _{2}-mathbf {s} _{1})}

en caso de

{displaystyle k_{1}k_{2}neq 1}

punto

{displaystyle S_{3}:mathbf {s} _{3}={frac {(1-k_{1})k_{2}mathbf {s} _{1}+(1-k_{2})mathbf {s} _{2}}{1-k_{1}k_{2}}}=mathbf {s} _{1}+{frac {1-k_{2}}{1-k_{1}k_{2}}}(mathbf {s} _{2}-mathbf {s} _{1})}

es un punto fijo (no se mueve) y la composición

{displaystyle sigma _{2}sigma _{1}: mathbf {x} to mathbf {s} _{3}+k_{1}k_{2}(mathbf {x} -mathbf {s} _{3})quad }

es un homothety con centro $S_{3}$ y ratio $k_1k_2$ . $S_{3}$ mentiras en línea ${displaystyle {overline {S_{1}S_{2}}}}$ .

La composición de una homoteca y una traducción es una homoteca.

Derivación:

La composición de la homotecia

{displaystyle sigma:mathbf {x} to mathbf {s} +k(mathbf {x} -mathbf {s}),;kneq 1,;}

y la traducción

{displaystyle tau:mathbf {x} to mathbf {x} +mathbf {v} }

{displaystyle tau sigma:mathbf {x} to mathbf {s} +mathbf {v} +k(mathbf {x} -mathbf {s})}

{displaystyle =mathbf {s} +{frac {mathbf {v} }{1-k}}+kleft(mathbf {x} -(mathbf {s} +{frac {mathbf {v} }{1-k}})right)}

que es una homoteca con centro ${displaystyle mathbf {s} '=mathbf {s} +{frac {mathbf {v} }{1-k}}}$ y ratio $k$ .

Showing translation for

In homogeneous coordinates

La homoteca ${displaystyle sigma:mathbf {x} to mathbf {s} +k(mathbf {x} -mathbf {s})}$ con centro ${displaystyle S=(u,v)}$ se puede escribir como la composición de una homoteca con centro $O$ y una traducción:

{displaystyle mathbf {x} to kmathbf {x} +(1-k)mathbf {s} }

Por lo tanto $sigma$ puede ser representado en coordenadas homogéneas por la matriz:

{displaystyle {begin{pmatrix}k&0&(1-k)u\0&k&(1-k)v\0&0&1end{pmatrix}}}

Una transformación lineal de homotecia pura también es conforme porque se compone de traslación y escala uniforme.

Contenido relacionado

Más resultados...