Historia del sistema de numeración hindú-árabe
El sistema de numeración hindú-árabe es un sistema de numeración de valor posicional decimal que utiliza un glifo cero como en "205".
Sus glifos son descendidos de los números indios Brahmi. El sistema completo surgió por los siglos VIII a IX, y se describe por primera vez fuera de la India en los Sobre la Cálculo con Numerales Hindúes (ca. 825), y el segundo trabajo de cuatro volúmenes de Al-Kindi Sobre el uso de los Numerosos Indios (ca. 830). Hoy el nombre Números hindú-árabes generalmente se utiliza.
Sistema decimal
Los historiadores remontan los números modernos en la mayoría de los idiomas a los números brahmi, que estaban en uso a mediados del siglo III a.C. El sistema de valor posicional, sin embargo, se desarrolló más tarde. Los números Brahmi se han encontrado en inscripciones en cuevas y en monedas en regiones cercanas a Pune, Maharashtra y Uttar Pradesh en la India. Estos números (con ligeras variaciones) estuvieron en uso hasta el siglo IV.
Durante el período Gupta (principios del siglo IV a finales del siglo VI), los números Gupta se desarrollaron a partir de los números Brahmi y el imperio Gupta los extendió por grandes áreas a medida que conquistaban territorio. A partir del siglo VII, los números Gupta se convirtieron en los números Nagari.
Desarrollo en la India
Durante el período védico (1500–500 a. C.), motivado por la construcción geométrica de los altares de fuego y la astronomía, el uso de un sistema numérico y de operaciones matemáticas básicas se desarrollaron en el norte de la India. La cosmología hindú requería el dominio de números muy grandes, como el kalpa (la vida del universo), que se dice es de 4.320.000.000 de años y la "órbita del cielo" se dice que son 18.712.069.200.000.000 yojanas. Los números se expresaron usando una "notación de valor posicional con nombre", usando nombres para las potencias de 10, como dasa, shatha, sahasra, ayuta, niyuta, prayuta, arbuda, nyarbuda, < i>samudra, madhya, anta, parardha etc., siendo el último de ellos el nombre de un billón (10< sup>12). Por ejemplo, el número 26.432 se expresó como "2 ayuta, 6 sahasra, 4 shatha, 3 dasa, 2." En el texto budista Lalitavistara, se dice que Buda narró un esquema de números hasta 1053.
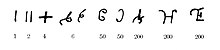
La forma de los números en las inscripciones de Ashoka en escritura brahmi (mediados del siglo III a. C.) implicaba signos separados para los números del 1 al 9, del 10 al 90, 100 y 1000. Un múltiplo de 100 o 1000 estaba representado por una modificación (o "cifrado") del signo del número utilizando el signo del número multiplicador. Dichos números cifrados representaban directamente los números de valor posicional nombrados utilizados verbalmente. Continuaron utilizándose en inscripciones hasta finales del siglo IX.
En su texto fundamental del año 499 EC, Aryabhata ideó un novedoso sistema numérico posicional, usando consonantes sánscritas para números pequeños y vocales para potencias de 10. Usando el sistema, números hasta mil millones podrían expresarse usando frases cortas, p. ej., khyu-ghṛ representa el número 4.320.000. El sistema no tuvo éxito porque producía frases bastante impronunciables, pero podría haber hecho entender el principio del sistema numérico posicional (llamado dasa-gunottara, exponentes de 10) a los matemáticos posteriores. En siglos posteriores se ideó un esquema katapayadi más elegante que representaba un sistema de valor posicional que incluía el cero.
Números de valor posicional sin cero

Si bien los números en textos e inscripciones usaban una notación de valor posicional con nombre, se podría haber empleado una notación más eficiente en los cálculos, posiblemente desde el siglo I d.C. Los cálculos se llevaban a cabo en tablillas de arcilla cubiertas con una fina capa de arena, dando origen al término dhuli-karana ('trabajo con arena') para cálculos superiores. Karl Menninger cree que, en tales cálculos, debieron prescindir de los números cifrados y escribir sólo secuencias de dígitos para representar los números. Un cero se habría representado como un "lugar faltante", como un punto. El único manuscrito con ejemplos elaborados que tenemos a nuestra disposición, el manuscrito Bakhshali (de fecha poco clara), utiliza un sistema de valor posicional con un punto para indicar el cero. El punto se llamaba shunya-sthāna 'lugar vacío'. El mismo símbolo también se usó en expresiones algebraicas para lo desconocido (como en la x canónica en el álgebra moderna).
Las referencias textuales a un sistema de valor posicional se ven desde el siglo V d.C. en adelante. Un comentario sobre los Yoga Sutras de Patanjali del siglo V dice: "Así como una línea en el lugar de las centenas [significa] cien, en las decenas, diez, y una en las unidades, así uno y la misma mujer se llama madre, hija y hermana."
Se empleó un sistema llamado bhūta-sankhya ('números objeto' o 'números concretos') para representar números en versos sánscritos, utilizando un concepto representar un dígito para representar el dígito mismo. El texto jainista titulado Lokavibhaga, fechado en 458 d.C., menciona el número objetivado
"panchabhyah khalu shunyebhyah param dve sapta chambaram ekam trini cha rupam cha"
que significa "cinco vacíos, luego dos y siete, el cielo, uno y tres y la forma", es decir, el número 13107200000. Estos números objetivados se utilizaron ampliamente desde el siglo VI en adelante, especialmente después de Varāhamihira. (c. siglo V d.C.). El cero se representa explícitamente en números como "el vacío" (sunya) o el "espacio-cielo" (ambara akasha). En consecuencia, el punto utilizado en lugar del cero en los números escritos se denominaba sunya-bindu.
Números de valor posicional con cero

En 628 EC, el astrónomo y matemático Brahmagupta escribió su texto Brahma Sphuta Siddhanta que contenía el primer tratamiento matemático del cero. Definió el cero como el resultado de restar un número de sí mismo, postuló los números negativos y analizó sus propiedades en operaciones aritméticas. Su palabra para cero era shunya (vacío), el mismo término utilizado anteriormente para el espacio vacío en el sistema de valor posicional de 9 dígitos. Esto proporcionó una nueva perspectiva sobre el shunya-bindu como numeral y allanó el camino para la eventual evolución de un dígito cero. El punto continuó utilizándose durante al menos 100 años después y se transmitió al sudeste asiático y Arabia. La escritura Sharada de Cachemira ha conservado el punto cero hasta el día de hoy.
A finales del siglo VII, los números decimales comienzan a aparecer en inscripciones en el sudeste asiático y en la India. Algunos estudiosos sostienen que aparecieron incluso antes. A menudo se cita una concesión en placa de cobre del siglo VI en Mankani que lleva el número 346 (correspondiente al 594 d.C.). Pero su fiabilidad es objeto de controversia. La primera aparición indiscutible de 0 en una inscripción ocurre en Gwalior en 876 EC, y contiene un número "270" en una notación sorprendentemente similar a la nuestra. A lo largo de los siglos VIII y IX, se utilizaron tanto los antiguos números brahmi como los nuevos números decimales, apareciendo en ocasiones en las mismas inscripciones. En algunos documentos, se ve que se produce una transición alrededor del año 866 d.C.
Adopción por los árabes
Antes del surgimiento del Califato, el sistema de numeración hindú-árabe ya se estaba desplazando hacia Occidente y fue mencionado en Siria en el año 662 d.C. por el erudito nestoriano siríaco Severus Sebokht, quien escribió lo siguiente:
- "Omitiré toda discusión sobre la ciencia de los indios, ..., de sus descubrimientos sutiles en la astronomía, descubrimientos que son más ingeniosos que los de los griegos y los babilonios, y de sus valiosos métodos de cálculo que superan la descripción. Sólo quiero decir que esta computación se hace por medio de nueve signos. Si aquellos que creen, porque hablan griego, que han llegado a los límites de la ciencia, leerían los textos indios, estarían convencidos, incluso si un poco tarde en el día, de que hay otros que saben algo de valor."
Según la Historia de los hombres eruditos de Al-Qifti:
- "... una persona de la India se presentó ante el califa al-Mansur en el año [776 dC] que estaba bien versado en el método de cálculo siddhanta relacionado con el movimiento de los cuerpos celestiales, y teniendo maneras de calcular ecuaciones basadas en el medio-chord [esencialmente el seno] calculado en medio-de acuerdo ... Todo esto está contenido en una obra... de la que él afirmó haber tomado el medio cuarto calculado por un minuto. Al-Mansur ordenó que este libro se tradujera al árabe, y un trabajo por escrito, basado en la traducción, para dar a los árabes una base sólida para calcular los movimientos de los planetas ..."
Lo más probable es que la obra haya sido Brāhmasphuṭasiddhānta (La apertura del universo) de Brahmagupta, escrita en el año 628. Independientemente de si esto es incorrecto, ya que todos los textos indios posteriores a Aryabhata& Aryabhatiya utilizó el sistema numérico indio; ciertamente, a partir de esta época los árabes tenían una traducción de un texto escrito en el sistema numérico indio.
En su texto La aritmética de Al-Uqlîdisî (Dordrecht: D. Reidel, 1978), A.S. Los estudios de Saidan no pudieron responder completamente cómo llegaron los números al mundo árabe:
- "Parece plausible que se desplara poco a poco, probablemente antes del siglo VII, a través de dos canales, uno a partir de Sind, sometiendo a la filtración persa y extendiéndose en lo que ahora se conoce como Oriente Medio, y el otro a partir de las costas del Océano Índico y extendiéndose a las costas meridionales del Mediterráneo".
Al-Uqlidisi desarrolló una notación para representar fracciones decimales. Los números saltaron a la fama debido a su uso en la obra fundamental del matemático persa Al-Khwarizmi, cuyo libro Sobre el cálculo con números hindúes fue escrito alrededor del año 825, y del matemático árabe Al-Kindi, que escribió cuatro volúmenes (ver [2]) "Sobre el uso de los números indios" (Ketab fi Isti'mal al-'Adad al-Hindi) alrededor del año 830. Ellos, entre otras obras, contribuyeron a la difusión del sistema de numeración indio en Oriente Medio y Occidente.
Desarrollo de símbolos
El desarrollo de los números a principios de Europa se muestra a continuación:
El ábaco versus el sistema de numeración hindú-árabe en las primeras imágenes modernas
Adopción en Europa
- 976. Los primeros números árabes en Europa aparecieron en Codex Vigilanus en el año 976.
- 1202. Fibonacci, un matemático italiano que había estudiado en Béjaïa (Bougie), Argelia, promovió el sistema de numeral árabe en Europa con su libro Liber Abaci, que se publicó en 1202.
- 1482. Sin embargo, el sistema no llegó a un amplio uso en Europa hasta la invención de la impresión. (Véase, por ejemplo, el mapa de 1482 Ptolemaeus del mundo impreso por Lienhart Holle en Ulm, y otros ejemplos en el Museo Gutenberg en Mainz (Alemania).
- 1512. Los números aparecen en su forma moderna en el título del “Conpusicion de la arte de la arismetica y juntamente de geometría” escrito por Juan de Ortega.
- 1549. Estos son el formato correcto y la secuencia del "números modernos"en la portada del Libro Intitulado Arithmetica Practica por Juan de Yciar, el caligrador y matemático vasco, Zaragoza 1549.
En los últimos siglos, la variedad europea de números arábigos se extendió por todo el mundo y poco a poco se convirtió en el sistema de numeración más utilizado en el mundo.
Incluso en muchos países con idiomas que tienen sus propios sistemas de numeración, los números arábigos europeos se utilizan ampliamente en el comercio y las matemáticas.
Impacto en la aritmética
La importancia del desarrollo del sistema numérico posicional es descrita por el matemático francés Pierre-Simon Laplace (1749–1827), quien escribió:
Es la India que nos dio el ingenioso método de expresar todos los números por medio de diez símbolos, cada símbolo recibiendo un valor de posición, así como un valor absoluto; una idea profunda e importante que parece tan simple para nosotros ahora que ignoramos su verdadero mérito, pero su misma simplicidad, la gran facilidad que ha prestado a todas las computaciones, pone nuestra aritmética en el primer rango de las invenciones útiles, y apreciaremos la grande mente de este genio











