Historia de la trigonometría

El estudio temprano de los triángulos se remonta al segundo milenio antes de Cristo, en las matemáticas egipcias (papiro matemático Rhind) y las matemáticas babilónicas. La trigonometría también prevalecía en las matemáticas kushitas. El estudio sistemático de las funciones trigonométricas comenzó en las matemáticas helenísticas y llegó a la India como parte de la astronomía helenística.En la astronomía india, el estudio de las funciones trigonométricas floreció en el período Gupta, especialmente debido a Aryabhata (siglo VI EC), quien descubrió la función seno. Durante la Edad Media, el estudio de la trigonometría continuó en las matemáticas islámicas, por matemáticos como Al-Khwarizmi y Abu al-Wafa. Se convirtió en una disciplina independiente en el mundo islámico, donde se conocían las seis funciones trigonométricas. Las traducciones de textos árabes y griegos llevaron a que la trigonometría se adoptara como materia en el Occidente latino a partir del Renacimiento con Regiomontanus. El desarrollo de la trigonometría moderna cambió durante el Siglo de las Luces occidental, comenzando con las matemáticas del siglo XVII (Isaac Newton y James Stirling) y alcanzando su forma moderna con Leonhard Euler (1748).

Etimología

El término "trigonometría" se deriva del griego τρίγωνον trigōnon, "triángulo" y μέτρον metron, "medida".

La palabra moderna "seno" se deriva de la palabra latina sinus, que significa "bahía", "seno" o "pliegue" indirectamente, a través de la transmisión india, persa y árabe, derivada del término griego khordḗ "cuerda de arco, cuerda". ". El término hindú para seno en sánscrito es jyā "cuerda de arco", los hindúes introdujeron originalmente y generalmente empleaban tres funciones trigonométricas jyā, koti-jyā y utkrama-jyā. Los hindúes los definieron como funciones de un arco de círculo, no de un ángulo, de ahí su asociación con la cuerda de un arco, y de ahí que la "cuerda de un arco" para el arco se llame "un arco" (dhanu, cāpa). Sus sinónimos son jivā, siñjini, maurvi, guna, etc. El sánscrito jīvā se tradujo (adoptó) al árabe como jiba, escrito jb جب. Luego, esto se interpretó como la palabra árabe genuina jayb, que significa "seno, pliegue, bahía", ya sea por los árabes o por un error de los traductores europeos como Robert de Chester, quien tradujo jayb al latín como seno. En particular, el arcus sinus rectus de Fibonacci demostró ser influyente en el establecimiento del término seno. Las palabras "minuto" y "segundo" se derivan de las frases latinas partes minutae primae y partes minutae secundae.Estos se traducen aproximadamente como "primeras piezas pequeñas" y "segundas piezas pequeñas".

Desarrollo

Antiguo Cercano Oriente

Los antiguos egipcios y babilonios conocían teoremas sobre las proporciones de los lados de triángulos similares durante muchos siglos. Sin embargo, como las sociedades prehelénicas carecían del concepto de medida de ángulo, se limitaban a estudiar los lados de los triángulos.

Los astrónomos babilónicos mantuvieron registros detallados sobre la salida y la puesta de las estrellas, el movimiento de los planetas y los eclipses solares y lunares, todo lo cual requería familiarizarse con las distancias angulares medidas en la esfera celeste. Con base en una interpretación de la tablilla cuneiforme Plimpton 322 (c. 1900 a. C.), algunos incluso han afirmado que los antiguos babilonios tenían una tabla de secantes, pero no funciona en este contexto, ya que sin el uso de círculos y ángulos en la situación ganó las notaciones trigonométricas modernas. no aplicar Sin embargo, existe mucho debate sobre si se trata de una tabla de ternas pitagóricas, una solución de ecuaciones cuadráticas o una tabla trigonométrica.

Los egipcios, por otro lado, utilizaron una forma primitiva de trigonometría para construir pirámides en el segundo milenio antes de Cristo. El papiro matemático Rhind, escrito por el escriba egipcio Ahmes (c. 1680-1620 a. C.), contiene el siguiente problema relacionado con la trigonometría:

"Si una pirámide tiene 250 codos de alto y el lado de su base 360 ​​codos de largo, ¿cuál es su tamaño ?"

La solución de Ahmes al problema es la relación entre la mitad del lado de la base de la pirámide y su altura, o la relación entre el recorrido y la elevación de su cara. En otras palabras, la cantidad que encontró para el seked es la cotangente del ángulo a la base de la pirámide y su cara.

Antigüedad clásica

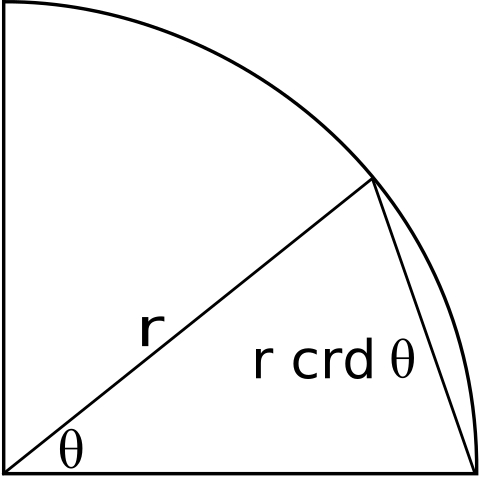
Los antiguos matemáticos griegos y helenísticos hicieron uso del acorde. Dado un círculo y un arco sobre el círculo, la cuerda es la línea que subtiende el arco. La bisectriz perpendicular de una cuerda pasa por el centro del círculo y biseca el ángulo. La mitad de la cuerda bisecada es el seno de la mitad del ángulo bisecado, es decir,

y, en consecuencia, la función seno también se conoce como semiacorde. Debido a esta relación, los matemáticos helenísticos también conocían una serie de identidades y teoremas trigonométricos que se conocen hoy en día, pero en su forma de cuerda equivalente.

Aunque no hay trigonometría en las obras de Euclides y Arquímedes, en el sentido estricto de la palabra, hay teoremas presentados de manera geométrica (en lugar de trigonométrica) que son equivalentes a leyes o fórmulas trigonométricas específicas. Por ejemplo, las proposiciones doce y trece del libro dos de los Elementos son las leyes de los cosenos para ángulos obtusos y agudos, respectivamente. Los teoremas sobre las longitudes de las cuerdas son aplicaciones de la ley de los senos. Y el teorema de Arquímedes sobre cuerdas rotas es equivalente a fórmulas para senos de sumas y diferencias de ángulos. Para compensar la falta de una tabla de cuerdas, los matemáticos de la época de Aristarco a veces usaban la afirmación de que, en la notación moderna, sen α / sen β < α / β < tan α /tan β siempre que 0° < β < α < 90°, ahora conocida como desigualdad de Aristarco.

Aparentemente, la primera tabla trigonométrica fue compilada por Hiparco de Nicea (180 - 125 a. C.), a quien ahora se le conoce como "el padre de la trigonometría". Hiparco fue el primero en tabular los valores correspondientes de arco y cuerda para una serie de ángulos.

Aunque no se sabe cuándo entró en las matemáticas el uso sistemático del círculo de 360°, se sabe que la introducción sistemática del círculo de 360° se produjo poco después de que Aristarco de Samos compusiera Sobre los tamaños y distancias del sol y la luna (ca.. 260 aC), ya que midió un ángulo en términos de una fracción de un cuadrante. Parece que el uso sistemático del círculo de 360° se debe en gran parte a Hiparco y su tabla de cuerdas. Hipparchus pudo haber tomado la idea de esta división de Hypsicles, quien anteriormente había dividido el día en 360 partes, una división del día que pudo haber sido sugerida por la astronomía babilónica.En la astronomía antigua, el zodíaco se dividía en doce "signos" o treinta y seis "decanatos". Un ciclo estacional de aproximadamente 360 ​​días podría haber correspondido a los signos y decanatos del zodíaco al dividir cada signo en treinta partes y cada decanato en diez partes. Es debido al sistema de numeración sexagesimal babilónico que cada grado se divide en sesenta minutos y cada minuto se divide en sesenta segundos.

Menelao de Alejandría (ca. 100 dC) escribió en tres libros su Sphaerica. En el Libro I, estableció una base para triángulos esféricos análoga a la base euclidiana para triángulos planos. Establece un teorema que no tiene análogo euclidiano, que dos triángulos esféricos son congruentes si los ángulos correspondientes son iguales, pero no distingue entre triángulos esféricos congruentes y simétricos. Otro teorema que establece es que la suma de los ángulos de un triángulo esférico es mayor a 180°. El Libro II de Sphaerica aplica la geometría esférica a la astronomía. Y el Libro III contiene el "teorema de Menelao". Además, dio su famosa "regla de las seis cantidades".

Más tarde, Claudio Ptolomeo (ca. 90 - ca. 168 d. C.) amplió los acordes en un círculo de Hipparchus en su Almagesto, o la sintaxis matemática. El Almagesto es principalmente un trabajo sobre astronomía, y la astronomía se basa en la trigonometría. La tabla de cuerdas de Ptolomeo da las longitudes de las cuerdas de un círculo de 120 de diámetro en función del número de grados n en el correspondiente arco del círculo, para n que va de 1/2 a 180 en incrementos de 1/2. Los trece libros del Almagesto son el trabajo trigonométrico más influyente y significativo de toda la antigüedad.Un teorema que fue fundamental para el cálculo de cuerdas de Ptolomeo fue lo que todavía se conoce hoy como el teorema de Ptolomeo, que la suma de los productos de los lados opuestos de un cuadrilátero cíclico es igual al producto de las diagonales. Un caso especial del teorema de Ptolomeo apareció como la proposición 93 en los Datos de Euclides. El teorema de Ptolomeo conduce al equivalente de las cuatro fórmulas de suma y diferencia para seno y coseno que hoy se conocen como fórmulas de Ptolomeo, aunque el propio Ptolomeo usó cuerdas en lugar de seno y coseno. Ptolomeo derivó además el equivalente de la fórmula del medio ángulo

Ptolomeo usó estos resultados para crear sus tablas trigonométricas, pero no se puede determinar si estas tablas se derivaron del trabajo de Hiparco.

Ni las tablas de Hipparchus ni las de Ptolomeo han sobrevivido hasta nuestros días, aunque las descripciones de otros autores antiguos dejan pocas dudas de que alguna vez existieron.

Pitágoras descubrió muchas de las propiedades de lo que se convertiría en funciones trigonométricas. El Teorema de Pitágoras, p + b = h es una representación de la identidad trigonométrica fundamental sen (x) + cos (x) = 1. La longitud 1 es la hipotenusa de cualquier triángulo rectángulo, y tiene catetos de longitud sen(x) y cos (x) siendo x uno de los dos ángulos no rectos. Con esto en mente, la identidad en la que se basa la trigonometría resulta ser el Teorema de Pitágoras.

Matemáticas indias

Algunos de los primeros y muy significativos desarrollos de la trigonometría se produjeron en la India. Obras influyentes de los siglos IV y V d. C., conocidas como los Siddhantas (de los cuales había cinco, el más importante de los cuales es el Surya Siddhanta) definieron primero el seno como la relación moderna entre la mitad de un ángulo y la mitad de una cuerda, mientras que también definiendo el coseno, el verseno y el seno inverso. Poco después, otro matemático y astrónomo indio, Aryabhata (476–550 d. C.), recopiló y amplió los desarrollos de los Siddhantas en un importante trabajo llamado Aryabhatiya. Los Siddhantas y los Aryabhatiya contienen las tablas más antiguas de valores de seno y valores de verseno (1 - coseno), en intervalos de 3,75 ° de 0 ° a 90 °, con una precisión de 4 decimales. Usaron las palabras jya para seno, kojya para coseno, utkrama-jya para versine y otkram jya para seno inverso. Las palabras jya y kojya eventualmente se convirtieron en seno y coseno respectivamente después de una mala traducción descrita anteriormente.

En el siglo VII, Bhaskara I produjo una fórmula para calcular el seno de un ángulo agudo sin el uso de una tabla. También dio la siguiente fórmula de aproximación para sen(x), que tenía un error relativo de menos del 1,9 %:

Más tarde, en el siglo VII, Brahmagupta volvió a desarrollar la fórmula

(también derivado anteriormente, como se mencionó anteriormente) y la fórmula de interpolación de Brahmagupta para calcular valores de seno.

Otro autor indio posterior sobre trigonometría fue Bhaskara II en el siglo XII. Bhaskara II desarrolló la trigonometría esférica y descubrió muchos resultados trigonométricos.

Bhaskara II fue uno de los primeros en descubrir resultados trigonométricos como :

• 

Madhava (c. 1400) hizo avances tempranos en el análisis de funciones trigonométricas y sus expansiones en series infinitas. Desarrolló los conceptos de la serie de potencias y la serie de Taylor, y produjo las expansiones de la serie de potencias de seno, coseno, tangente y arcotangente. Usando las aproximaciones de la serie de Taylor de seno y coseno, produjo una tabla de senos con 12 decimales de precisión y una tabla de cosenos con 9 decimales de precisión. También dio la serie de potencias de π y el ángulo, radio, diámetro y circunferencia de un círculo en términos de funciones trigonométricas. Sus obras fueron ampliadas por sus seguidores en la Escuela de Kerala hasta el siglo XVI.

No.	Serie	Nombre	Descubridores occidentales de la seriey fechas aproximadas de descubrimiento.
1	sen x = x − x / 3! + x /5! − x / 7! +...	Serie de senos de Madhava	Isaac Newton (1670) y Wilhelm Leibniz (1676)
2	porque x = 1 − x / 2! + x /4! − x / 6! +...	Serie coseno de Madhava	Isaac Newton (1670) y Wilhelm Leibniz (1676)
3	bronceado x = x − x / 3 + x / 5 − x / 7 +...	Serie arcotangente de Madhava	James Gregory (1671) y Wilhelm Leibniz (1676)

El texto indio Yuktibhāṣā contiene pruebas de la expansión de las funciones seno y coseno y la derivación y prueba de la serie de potencias para la tangente inversa, descubierta por Madhava. El Yuktibhāṣā también contiene reglas para encontrar los senos y los cosenos de la suma y la diferencia de dos ángulos.

Matemáticas chinas

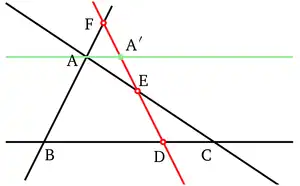
En China, la tabla de senos de Aryabhata se tradujo al libro matemático chino Kaiyuan Zhanjing, compilado en el año 718 d. C. durante la dinastía Tang. Aunque los chinos sobresalieron en otros campos de las matemáticas, como la geometría sólida, el teorema del binomio y las fórmulas algebraicas complejas, las primeras formas de trigonometría no fueron tan apreciadas como en los primeros mundos griego, helenístico, indio e islámico. En cambio, los primeros chinos usaron un sustituto empírico conocido como chong cha, mientras que se conocía el uso práctico de la trigonometría plana al usar el seno, la tangente y la secante.Sin embargo, este estado embrionario de la trigonometría en China comenzó a cambiar y avanzar lentamente durante la dinastía Song (960-1279), cuando los matemáticos chinos comenzaron a enfatizar más la necesidad de la trigonometría esférica en la ciencia calendárica y los cálculos astronómicos. El erudito científico, matemático y funcionario chino Shen Kuo (1031-1095) utilizó funciones trigonométricas para resolver problemas matemáticos de cuerdas y arcos. Victor J. Katz escribe que en la fórmula de Shen "técnica de círculos que se cortan", creó una aproximación del arco s de un círculo dado el diámetro d, sagitta v y longitud c de la cuerda que subtiende el arco, cuya longitud él aproximado como

Sal Restivo escribe que el trabajo de Shen sobre las longitudes de los arcos de círculos proporcionó la base para la trigonometría esférica desarrollada en el siglo XIII por el matemático y astrónomo Guo Shoujing (1231-1316). Como afirman los historiadores L. Gauchet y Joseph Needham, Guo Shoujing utilizó la trigonometría esférica en sus cálculos para mejorar el sistema calendárico y la astronomía china. Junto con una ilustración china posterior del siglo XVII de las pruebas matemáticas de Guo, Needham afirma que:

Guo usó una pirámide esférica cuadrangular, cuyo cuadrilátero basal constaba de un arco ecuatorial y otro eclíptico, junto con dos arcos meridianos, uno de los cuales pasaba por el punto del solsticio de verano... Mediante tales métodos pudo obtener el du lü. (grados del ecuador correspondientes a grados de la eclíptica), el ji cha (valores de cuerdas para arcos eclípticos dados) y el cha lü (diferencia entre cuerdas de arcos que difieren en 1 grado).

A pesar de los logros del trabajo de Shen y Guo en trigonometría, no se volvería a publicar otro trabajo sustancial en trigonometría china hasta 1607, con la publicación dual de los Elementos de Euclides por el funcionario y astrónomo chino Xu Guangqi (1562-1633) y el jesuita italiano Matteo Ricci. (1552-1610).

Mundo islámico medieval

Los trabajos anteriores fueron posteriormente traducidos y ampliados en el mundo islámico medieval por matemáticos musulmanes de ascendencia mayoritariamente persa y árabe, quienes enunciaron una gran cantidad de teoremas que liberaron al tema de la trigonometría de la dependencia del cuadrilátero completo, como fue el caso de las matemáticas helenísticas debido a a la aplicación del teorema de Menelao. Según ES Kennedy, fue después de este desarrollo de las matemáticas islámicas que "surgió la primera trigonometría real, en el sentido de que sólo entonces el objeto de estudio se convirtió en el triángulo esférico o plano, sus lados y ángulos".

También se conocían métodos relacionados con triángulos esféricos, en particular el método de Menelao de Alejandría, quien desarrolló el "teorema de Menelao" para tratar problemas esféricos. Sin embargo, ES Kennedy señala que si bien en las matemáticas preislámicas era posible calcular las magnitudes de una figura esférica, en principio, mediante el uso de la tabla de cuerdas y el teorema de Menelao, la aplicación del teorema a problemas esféricos era muy difícil en la práctica.Para observar los días sagrados en el calendario islámico en el que los tiempos se determinaban por las fases de la luna, los astrónomos utilizaron inicialmente el método de Menelao para calcular el lugar de la luna y las estrellas, aunque este método resultó ser torpe y difícil. Se trataba de establecer dos triángulos rectángulos que se cruzan; aplicando el teorema de Menelao era posible resolver uno de los seis lados, pero solo si se conocían los otros cinco lados. Para saber la hora a partir de la altura del sol, por ejemplo, se requerían aplicaciones repetidas del teorema de Menelao. Para los astrónomos islámicos medievales, había un desafío obvio para encontrar un método trigonométrico más simple.

A principios del siglo IX d. C., Muhammad ibn Mūsā al-Khwārizmī produjo tablas precisas de senos y cosenos, y la primera tabla de tangentes. También fue un pionero en trigonometría esférica. En 830 dC, Habash al-Hasib al-Marwazi produjo la primera tabla de cotangentes. Muhammad ibn Jābir al-Harrānī al-Battānī (Albatenius) (853-929 d. C.) descubrió las funciones recíprocas de secante y cosecante, y produjo la primera tabla de cosecantes para cada grado de 1° a 90°.

En el siglo X d. C., en el trabajo de Abū al-Wafā' al-Būzjānī, los matemáticos musulmanes usaban las seis funciones trigonométricas. Abu al-Wafa tenía tablas de senos en incrementos de 0,25 °, con 8 decimales de precisión y tablas precisas de valores de tangente. También desarrolló la siguiente fórmula trigonométrica:(un caso especial de la fórmula de suma de ángulos de Ptolomeo; ver arriba)

En su texto original, Abū al-Wafā' afirma: "Si queremos eso, multiplicamos el seno dado por los minutos del coseno, y el resultado es la mitad del seno del doble". Abū al-Wafā también estableció las identidades de adición y diferencia de ángulos presentadas con pruebas completas:

Para el segundo, el texto dice: "Multiplicamos el seno de cada uno de los dos arcos por el coseno de los otros minutos. Si queremos el seno de la suma, sumamos los productos, si queremos el seno de la diferencia, tomamos su diferencia".

También descubrió la ley de los senos para la trigonometría esférica:

También a fines del siglo X y principios del XI d.C., el astrónomo egipcio Ibn Yunus realizó muchos cálculos trigonométricos cuidadosos y demostró la siguiente identidad trigonométrica:

Al-Jayyani (989-1079) de al-Andalus escribió El libro de los arcos desconocidos de una esfera, que se considera "el primer tratado de trigonometría esférica". "Contiene fórmulas para triángulos derechos, la ley general de los senos y la solución de un triángulo esférico por medio del triángulo polar". Este tratado tuvo más tarde una "fuerte influencia en las matemáticas europeas", y es probable que su "definición de proporciones como números" y "método para resolver un triángulo esférico cuando se desconocen todos los lados" hayan influido en Regiomontanus.

El método de triangulación fue desarrollado por primera vez por matemáticos musulmanes, quienes lo aplicaron a usos prácticos como la topografía y la geografía islámica, como lo describió Abu Rayhan Biruni a principios del siglo XI. El propio Biruni introdujo técnicas de triangulación para medir el tamaño de la Tierra y las distancias entre varios lugares. A fines del siglo XI, Omar Khayyám (1048–1131) resolvió ecuaciones cúbicas usando soluciones numéricas aproximadas encontradas por interpolación en tablas trigonométricas. En el siglo XIII, Nasīr al-Dīn al-Tūsī fue el primero en tratar la trigonometría como una disciplina matemática independiente de la astronomía, y desarrolló la trigonometría esférica hasta su forma actual. Enumeró los seis casos distintos de un triángulo rectángulo en trigonometría esférica, y en suEn la figura del sector, estableció la ley de los senos para triángulos planos y esféricos, descubrió la ley de tangentes para triángulos esféricos y proporcionó pruebas para ambas leyes. Nasir al-Din al-Tusi ha sido descrito como el creador de la trigonometría como una disciplina matemática por derecho propio.

En el siglo XV, Jamshīd al-Kāshī proporcionó la primera declaración explícita de la ley de los cosenos en una forma adecuada para la triangulación. En Francia, la ley de los cosenos todavía se conoce como el teorema de Al-Kashi. También dio tablas trigonométricas de valores de la función seno a cuatro dígitos sexagesimales (equivalentes a 8 decimales) por cada 1° de argumento con diferencias a sumar por cada 1/60 de 1°. Ulugh Beg también proporciona tablas precisas de senos y tangentes con 8 decimales aproximadamente al mismo tiempo.

Renacimiento europeo y después.

En 1342, Levi ben Gershon, conocido como Gersonides, escribió Sobre senos, cuerdas y arcos, en particular demostrando la ley de los senos para triángulos planos y dando tablas de senos de cinco cifras.

Una tabla trigonométrica simplificada, la " toleta de marteloio ", fue utilizada por los marineros en el Mar Mediterráneo durante los siglos XIV-XV para calcular los cursos de navegación. Está descrito por Ramon Llull de Mallorca en 1295 y recogido en el atlas de 1436 del capitán veneciano Andrea Bianco.

Regiomontanus fue quizás el primer matemático en Europa en tratar la trigonometría como una disciplina matemática distinta, en su De triangulis omnimodis escrito en 1464, así como en su posterior Tabulae directionum que incluía la función tangente, sin nombre. El Opus palatinum de triangulis de Georg Joachim Rheticus, estudiante de Copérnico, fue probablemente el primero en Europa en definir funciones trigonométricas directamente en términos de triángulos rectángulos en lugar de círculos, con tablas para las seis funciones trigonométricas; este trabajo fue terminado por el alumno de Rheticus Valentin Otho en 1596.

En el siglo XVII, Isaac Newton y James Stirling desarrollaron la fórmula general de interpolación Newton-Stirling para funciones trigonométricas.

En el siglo XVIII, la Introducción de Leonhard Euler en analysin infinitorum (1748) fue la principal responsable de establecer el tratamiento analítico de las funciones trigonométricas en Europa, derivando sus series infinitas y presentando la "fórmula de Euler" e = cos x + i sen x. Euler usó las abreviaturas casi modernas sin. , porque , Tang. , cuna. , seg. , y cosec. Antes de esto, Roger Cotes había calculado la derivada del seno en su Harmonia Mensurarum (1722). También en el siglo XVIII, Brook Taylor definió la serie general de Taylor y dio las expansiones y aproximaciones de la serie para las seis funciones trigonométricas. Los trabajos de James Gregory en el siglo XVII y Colin Maclaurin en el siglo XVIII también fueron muy influyentes en el desarrollo de las series trigonométricas.