Historia de la teoría gravitacional

Pioneers of gravitational theory

Aristotle

Galileo Galilei

Isaac Newton

Albert Einstein

En física, las teorías de la gravitación postulan mecanismos de interacción que rigen los movimientos de los cuerpos con masa. Desde la antigüedad, han existido numerosas teorías de la gravitación. Las primeras fuentes existentes que tratan de dichas teorías se encuentran en la filosofía griega antigua. Este trabajo fue impulsado durante la Edad Media por científicos indios, islámicos y europeos, antes de lograr grandes avances durante el Renacimiento y la Revolución Científica, que culminaron en la formulación de la ley de la gravedad de Newton. Esta fue reemplazada por la teoría de la relatividad de Albert Einstein a principios del siglo XX.

El filósofo griego Aristóteles (fl. siglo IV a.C.) descubrió que los objetos sumergidos en un medio tienden a caer a velocidades proporcionales a su peso. Vitruvio (fl. siglo I a.C.) entendió que los objetos caen en función de su gravedad específica. En el siglo VI d.C., el erudito alejandrino bizantino Juan Filópono modificó el concepto aristotélico de gravedad con la teoría del ímpetu. En el siglo VII, el astrónomo indio Brahmagupta habló de la gravedad como una fuerza atractiva. En el siglo XIV, los filósofos europeos Jean Buridan y Alberto de Sajonia, influidos por ciertos eruditos islámicos, desarrollaron la teoría del impulso y la relacionaron con la aceleración y la masa de los objetos. Alberto también desarrolló una ley de proporción sobre la relación entre la velocidad de un objeto en caída libre y el tiempo transcurrido.

Los italianos del siglo XVI descubrieron que los objetos en caída libre tienden a acelerarse de la misma manera. En 1632, Galileo Galilei formuló el principio básico de la relatividad. La existencia de la constante gravitacional fue explorada por varios investigadores desde mediados del siglo XVII, lo que ayudó a Isaac Newton a formular su ley de gravitación universal. La mecánica clásica de Newton fue reemplazada a principios del siglo XX, cuando Einstein desarrolló las teorías especial y general de la relatividad. En los enfoques de la gravedad cuántica, como la teoría de cuerdas, se plantea la hipótesis de un portador de fuerza elemental de la gravedad, en una teoría potencialmente unificada del todo.

El filósofo griego jónico Heráclito (c. 535 – c. 475 a. C.) utilizó la palabra logos ('palabra') para describir un tipo de ley que mantiene el cosmos en armonía, moviendo todos los objetos, incluidas las estrellas, los vientos y las olas.

El antiguo atomista Leucipo (siglo V a. C.) propuso que el cosmos se creó cuando un gran grupo de átomos se unió y giró en un vórtice. Los átomos más pequeños se convirtieron en los cuerpos celestes del cosmos. Los átomos más grandes del centro se unieron para formar una membrana a partir de la cual se formó la Tierra.

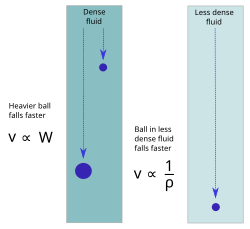
En el siglo IV a. C., el filósofo griego Aristóteles enseñó que no hay efecto ni movimiento sin una causa. La causa del movimiento natural descendente de los cuerpos pesados, como los elementos tierra y agua, estaba relacionada con su naturaleza (gravedad), que los hacía moverse hacia abajo, hacia el centro del universo (geocéntrico). Por esta razón, Aristóteles defendía una Tierra esférica, ya que «cada porción de la Tierra tiene peso hasta que alcanza el centro, y el empuje de las partes más grandes y más pequeñas no produciría una superficie ondulada, sino más bien una compresión y convergencia de parte a parte hasta que se alcanzara el centro». Por otro lado, los cuerpos ligeros, como los elementos fuego y aire, se movían por su naturaleza (levedad) hacia arriba, hacia la esfera celeste de la Luna (véase esfera sublunar). Los objetos astronómicos cercanos a las estrellas fijas están compuestos de éter, cuyo movimiento natural es circular. Más allá de ellos se encuentra el motor primario, la causa final de todo movimiento en el cosmos. En su Física, Aristóteles afirmó correctamente que los objetos sumergidos en un medio tienden a caer a velocidades proporcionales a su peso e inversamente proporcionales a la densidad del medio.

El filósofo griego Estratón de Lámpsaco (c. 335 – c. 269 a. C.) rechazó la creencia aristotélica de los "lugares naturales" a cambio de una visión mecanicista según la cual los objetos no ganan peso al caer, argumentando en cambio que el mayor impacto se debía a un aumento de la velocidad.

Epicuro (c. 341–270 a. C.) consideraba que el peso era una propiedad inherente de los átomos que influye en su movimiento. Estos átomos se mueven hacia abajo en caída libre constante dentro de un vacío infinito sin resistencia a la misma velocidad, independientemente de su masa. Por otro lado, el movimiento hacia arriba se debe a las colisiones atómicas. Los epicúreos se desviaron de las teorías atomistas más antiguas, como la de Demócrito (c. 460–c. 370 a. C.) al proponer la idea de que los átomos pueden desviarse aleatoriamente de su curso esperado.

El astrónomo griego Aristarco de Samos (c. 310 – c. 230 a. C.) teorizó la rotación de la Tierra sobre su propio eje y la órbita de la Tierra alrededor del Sol en una cosmología heliocéntrica. Seleuco de Seleucia (c. 190 – c. 150 a. C.) apoyó su cosmología y también describió los efectos gravitacionales de la Luna sobre la amplitud de las mareas.

El físico griego del siglo III a. C. Arquímedes (c. 287 – c. 212 a. C.) descubrió el centro de masas de un triángulo. También postuló que si los centros de gravedad de dos pesos iguales no fueran los mismos, estarían ubicados en el medio de la línea que los une. En Sobre los cuerpos flotantes, Arquímedes afirmó que para cualquier objeto sumergido en un fluido existe una fuerza de flotación ascendente equivalente al peso del fluido desplazado por el volumen del objeto. Los fluidos descritos por Arquímedes no son autogravitantes, ya que supone que "cualquier fluido en reposo es la superficie de una esfera cuyo centro es el mismo que el de la Tierra".

El astrónomo griego Hiparco de Nicea (c. 190 – c. 120 a. C.) también rechazó la física aristotélica y siguió a Estratón al adoptar alguna forma de teoría del impulso para explicar el movimiento. El poema De rerum natura de Lucrecio (c. 99 – c. 55 a. C.) afirma que los cuerpos más masivos caen más rápido en un medio porque este último resiste menos, pero en el vacío caen con la misma velocidad. El ingeniero y arquitecto romano Vitruvio (c. 85 – c. 15 a. C.) sostiene en su De architectura que la gravedad no depende del peso de una sustancia sino más bien de su "naturaleza" (cf. gravedad específica):

Si el velocista es derramado en un vaso, y una piedra que pesa cien libras sobre él, la piedra nada sobre la superficie, y no puede deprimir el líquido, ni atravesarlo, ni separarlo. Si quitamos el peso de cien libras, y ponemos un escrúpulo de oro, no nadará, pero se hundirá al fondo de su propio acuerdo. Por lo tanto, es innegable que la gravedad de una sustancia no depende de la cantidad de su peso, sino de su naturaleza.

El filósofo griego Plutarco (c. 46 – 120 d. C.) atestiguó la existencia de astrónomos romanos que rechazaban la física aristotélica, "incluso contemplaban teorías de inercia y gravitación universal", y sugirieron que la atracción gravitatoria no era exclusiva de la Tierra. Los efectos gravitatorios de la Luna sobre las mareas fueron observados por Plinio el Viejo (23–79 d. C.) en su Naturalis Historia y Claudio Ptolomeo (100 – c. 170 d. C.) en su Tetrabiblos.

En el siglo VI d. C., el erudito alejandrino bizantino Juan Filópono propuso la teoría del ímpetu, que modifica la teoría de Aristóteles de que "la continuación del movimiento depende de la acción continua de una fuerza" al incorporar una fuerza causal que disminuye con el tiempo. En su comentario a la Física de Aristóteles dice que "si uno deja caer simultáneamente desde la misma altura dos cuerpos que difieren mucho en peso, se encontrará que la relación de los tiempos de su movimiento no corresponde a la relación de sus pesos, sino que la diferencia en el tiempo es muy pequeña".

Brahmagupta (c. 598 – c. 668 d. C.) fue el primero entre los matemáticos y astrónomos indios en describir la gravedad como una fuerza atractiva utilizando el término "gurutvākarṣaṇam (गुरुत्वाकर्षणम्)":

La tierra en todos sus lados es la misma; toda la gente en la tierra se levanta, y todas las cosas pesadas caen a la tierra por una ley de la naturaleza, porque es la naturaleza de la tierra para atraer y mantener las cosas, como es la naturaleza del agua para fluir... Si una cosa quiere ir más abajo que la tierra, déjala intentarlo. La tierra es la única bajo cosa, y las semillas siempre vuelven a ella, en cualquier dirección que puedas tirarlas, y nunca se levantan hacia arriba de la tierra.

Otro famoso matemático y astrónomo indio, Bhāskarā II (Bhāskarāchārya, "Bhāskara, el maestro", c. 1114 – c. 1185), describe la gravedad como una propiedad atractiva inherente de la Tierra en la sección Golādhyāyah (Sobre las esferas) de su tratado Siddhānta Shiromani:

La propiedad de la atracción es inherente en la Tierra. Por esta propiedad la Tierra atrae cualquier cosa pesada no apoyada hacia ella: La cosa parece estar cayendo pero está en un estado de ser arrastrada a la Tierra.... Se manifiesta de esto que... personas situadas a distancias de una cuarta parte de la circunferencia [de la tierra] de nosotros o en el hemisferio opuesto, no pueden por ningún medio caer hacia abajo [en el espacio].

En el siglo XI d. C., el erudito persa Ibn Sina (Avicena) coincidió con la teoría de Filópono de que "el objeto en movimiento adquiere una inclinación a partir del motor" como explicación del movimiento de un proyectil. Ibn Sina publicó después su propia teoría del ímpetu en El libro de la curación (c. 1020). A diferencia de Filópono, que creía que se trataba de una virtud temporal que decaería incluso en el vacío, Ibn Sina la consideraba persistente y requería fuerzas externas como la resistencia del aire para disiparla. Ibn Sina hizo una distinción entre "fuerza" e "inclinación" (mayl) y sostuvo que un objeto ganaba mayl cuando se oponía a su movimiento natural. Concluyó que la continuación del movimiento se atribuye a la inclinación que se transfiere al objeto, y que el objeto estará en movimiento hasta que se agote el mayl. El erudito iraquí Ibn al-Haytham describe la gravedad como una fuerza por la cual un cuerpo más pesado se mueve hacia el centro de la Tierra. También describe que la fuerza de la gravedad solo se moverá hacia la dirección del centro de la Tierra, no en direcciones diferentes.

Otro erudito persa del siglo XI, Al-Biruni, propuso que los cuerpos celestes tienen masa, peso y gravedad, al igual que la Tierra. Criticó tanto a Aristóteles como a Ibn Sina por sostener la opinión de que sólo la Tierra tiene estas propiedades. El erudito del siglo XII Al-Khazini sugirió que la gravedad que contiene un objeto varía según su distancia al centro del universo (refiriéndose al centro de la Tierra). Al-Biruni y Al-Khazini estudiaron la teoría del centro de gravedad y la generalizaron y aplicaron a los cuerpos tridimensionales. También se desarrollaron métodos experimentales de gran calidad para determinar la gravedad específica o el peso específico de los objetos, basándose en la teoría de las balanzas y el pesaje.

En el siglo XII, Abu'l-Barakāt al-Baghdādī adoptó y modificó la teoría de Ibn Sina sobre el movimiento de proyectiles. En su Kitab al-Mu'tabar, Abu'l-Barakat afirmó que el motor imparte una inclinación violenta (mayl qasri) sobre el objeto en movimiento y que esta disminuye a medida que el objeto en movimiento se distancia del motor. Según Shlomo Pines, la teoría del movimiento de al-Baghdādī era "la negación más antigua de la ley dinámica fundamental de Aristóteles [es decir, que una fuerza constante produce un movimiento uniforme], [y es por lo tanto una] anticipación de manera vaga de la ley fundamental de la mecánica clásica [es decir, que una fuerza aplicada continuamente produce aceleración]".

En el siglo XIV, tanto el filósofo francés Jean Buridan como los calculistas de Oxford (la Escuela Merton) del Merton College de Oxford rechazaron el concepto aristotélico de gravedad. Atribuían el movimiento de los objetos a un ímpetu (similar al momento), que varía según la velocidad y la masa; Buridan recibió la influencia del Libro de la curación de Ibn Sina. Buridan y el filósofo Alberto de Sajonia (c. 1320-1390) adoptaron la teoría de Abu'l-Barakat de que la aceleración de un cuerpo que cae es el resultado de su ímpetu creciente. Influenciado por Buridan, Alberto desarrolló una ley de proporción sobre la relación entre la velocidad de un objeto en caída libre y el tiempo transcurrido. También teorizó que las montañas y los valles son causados por la erosión, que desplaza el centro de gravedad de la Tierra.

Las raíces de la expresión de Domingo de Soto movimiento uniformemente acelerado (uniform difform) se encuentran en los términos movimiento "uniforme" y movimiento "difforme" de los Calculadores de Oxford. El movimiento "uniforme" se utilizaba de forma diferente en aquel entonces que en la actualidad. El movimiento "uniforme" podría referirse tanto a la velocidad constante como al movimiento en el que todas las partes de un cuerpo se mueven a la misma velocidad. Aparentemente, los Calculadores no ilustraron los diferentes tipos de movimiento con ejemplos del mundo real. John of Holland, de la Universidad de Praga, ilustró el movimiento uniforme con lo que más tarde se llamaría velocidad uniforme, pero también con una piedra que cae (todas las partes se mueven a la misma velocidad) y con una esfera en rotación uniforme. Sin embargo, hizo distinciones entre diferentes tipos de movimiento "uniforme". El movimiento difforme se ejemplificó caminando a una velocidad creciente.

También en el siglo XIV, la Escuela de Merton desarrolló el teorema de la velocidad media: un cuerpo uniformemente acelerado que parte del reposo recorre la misma distancia que un cuerpo con velocidad uniforme cuya velocidad es la mitad de la velocidad final del cuerpo acelerado. El teorema de la velocidad media fue demostrado por Nicole Oresme (c. 1323–1382) y sería influyente en ecuaciones gravitacionales posteriores. Escrito como una ecuación moderna:

${\displaystyle \ s={\frac {1}{2}v_{f}t}$

Sin embargo, como no se podían medir intervalos de tiempo pequeños, la relación entre el tiempo y la distancia no era tan evidente como sugiere la ecuación. En términos más generales, las ecuaciones, que no se usaron ampliamente hasta después de la época de Galileo, implican una claridad que no existía.

Leonardo da Vinci (1452-1519) hizo dibujos que registraban la aceleración de los objetos que caían. Escribió que la "madre y origen de la gravedad" es la energía. Describe dos pares de poderes físicos que surgen de un origen metafísico y tienen un efecto sobre todo: abundancia de fuerza y movimiento, y gravedad y resistencia. Asocia la gravedad con los elementos clásicos "fríos", el agua y la tierra, y llama a su energía infinita. En el Codex Arundel, Leonardo registró que si un jarrón que vierte agua se mueve transversalmente (de lado), simulando la trayectoria de un objeto que cae verticalmente, produce un triángulo rectángulo con la misma longitud de catetos, compuesto por el material que cae que forma la hipotenusa y la trayectoria del jarrón que forma uno de los catetos. En la hipotenusa, Leonardo señaló la equivalencia de los dos movimientos ortogonales, uno efectuado por la gravedad y el otro propuesto por el experimentador.

En 1514, Nicolás Copérnico había escrito un esbozo de su modelo heliocéntrico, en el que afirmaba que el centro de la Tierra es el centro tanto de su rotación como de la órbita de la Luna. En 1533, el humanista alemán Petrus Apianus describió el ejercicio de la gravedad:

Puesto que es evidente que en el descenso [durante el arco] hay más impedimento adquirido, está claro que la gravedad se disminuye en esta cuenta. Pero porque esto viene por razón de la posición de los cuerpos pesados, que se llame una gravedad posicional [es decir. gravedad secundum situm]

En 1544, según Benedetto Varchi, los experimentos de al menos dos italianos, Francesco Beato, filósofo dominico de Pisa, y Luca Ghini, médico y botánico de Bolonia, habían disipado la afirmación aristotélica de que los objetos caen a velocidades proporcionales a su peso.

En 1551, Domingo de Soto teorizó que los objetos en caída libre se aceleran de manera uniforme en su libro Physicorum Aristotelis quaestiones. Esta idea fue explorada posteriormente con más detalle por Galileo Galilei, quien derivó su cinemática del Merton College del siglo XIV y de Jean Buridan, y posiblemente también de De Soto.

En 1585, el erudito flamenco Simon Stevin realizó una demostración para Jan Cornets de Groot, un político local de la ciudad holandesa de Delft. Stevin dejó caer dos bolas de plomo desde la Nieuwe Kerk de esa ciudad. A partir del sonido de los impactos, Stevin dedujo que las bolas habían caído a la misma velocidad. El resultado se publicó en 1586.

Tomemos (como... Jan Cornets de Groot... y he hecho) dos bolas de plomo, la una diez veces más grande y más pesado que la otra, y déjelas juntas desde una altura de 30 pies en un tablero o algo en el que dan un sonido perceptible. Entonces se encontrará que el más ligero no será diez veces más largo en su camino que el más pesado, pero que caen juntos en el tablero de modo que simultáneamente sus dos sonidos parecen ser uno y el mismo.... Por lo tanto Aristóteles... está equivocado.

—Simon Stevin, De Beghinselen der Weeghconst

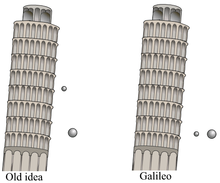
Entre 1589 y 1592 se dice que el científico italiano Galileo Galilei (entonces profesor de matemáticas en la Universidad de Pisa) ha bajado "pesos desiguales del mismo material" de la Torre de Pisa para demostrar que su tiempo de descenso era independiente de su masa, según una biografía del alumno de Galileo Vincenzo Viviani, compuesta en 1654 y publicada en 1717. La premisa básica ya había sido demostrada por los experimentadores italianos unas décadas antes.

Según la historia, Galileo descubrió a través de este experimento que los objetos cayeron con la misma aceleración, demostrando su predicción verdadera, mientras al mismo tiempo desprobando la teoría de gravedad de Aristóteles (que afirma que los objetos caen a velocidad proporcional a su masa). La mayoría de los historiadores consideran que ha sido un experimento de pensamiento en lugar de una prueba física.

Galileo aplicó con éxito las matemáticas a la aceleración de la caída de objetos, planteando correctamente en una carta de 1604 a Paolo Sarpi la hipótesis de que la distancia de un objeto en caída es proporcional al cuadrado del tiempo transcurrido.

He llegado a una propuesta, es decir, que los espacios atravesados en movimiento natural están en la proporción cuadrada de los tiempos.

—Galileo Galilei, Carta a Paolo Sarpi

Escrito con símbolos modernos: s ∝ t²

El resultado fue publicado en Two New Sciences en 1638. En el mismo libro, Galileo sugirió que la ligera variación de la velocidad de caída de objetos de diferente masa se debía a la resistencia del aire, y que los objetos caerían de manera completamente uniforme en el vacío. La relación entre la distancia de los objetos en caída libre y el cuadrado del tiempo empleado fue confirmada por los jesuitas italianos Grimaldi y Riccioli entre 1640 y 1650. También realizaron un cálculo de la gravedad de la Tierra registrando las oscilaciones de un péndulo.

En su Astronomia nova (1609), Johannes Kepler propuso una fuerza de atracción de radio limitado entre cuerpos "afines":

La gravedad es una disposición corpórea mutua entre cuerpos encendidos para unir o unirse; así la tierra atrae una piedra mucho más que la piedra busca la tierra. (La facultad magnética es otro ejemplo de este tipo).... Si dos piedras se colocaran cerca una de la otra en algún lugar del mundo fuera de la esfera de influencia de un cuerpo de tercera clase, estas piedras, como dos cuerpos magnéticos, se unirían en un lugar intermedio, cada uno acercándose al otro por un espacio proporcional al grueso [toposDel otro...

Un discípulo de Galileo, Evangelista Torricelli reiteró el modelo de Aristóteles que implica un centro gravitacional, añadiendo su opinión de que un sistema sólo puede estar en equilibrio cuando el propio centro común es incapaz de caer.

La relación entre la distancia de los objetos en caída libre y el cuadrado del tiempo empleado fue confirmada por Francesco Maria Grimaldi y Giovanni Battista Riccioli entre 1640 y 1650. También calcularon la gravedad de la Tierra constante mediante el registro de las oscilaciones de un péndulo.

En 1644, René Descartes propuso que no puede existir ningún espacio vacío y que un continuo de materia hace que todo movimiento sea curvilíneo. Así, la fuerza centrífuga empuja la materia relativamente ligera lejos de los vórtices centrales de los cuerpos celestes, reduciendo la densidad localmente y creando así una presión centrípeta. Utilizando aspectos de esta teoría, entre 1669 y 1690, Christiaan Huygens diseñó un modelo matemático de vórtice. En una de sus pruebas, demuestra que la distancia recorrida por un objeto que se deja caer desde una rueda giratoria aumentará proporcionalmente al cuadrado del tiempo de rotación de la rueda. En 1671, Robert Hooke especuló que la gravitación es el resultado de cuerpos que emiten ondas en el éter. Nicolas Fatio de Duillier (1690) y Georges-Louis Le Sage (1748) propusieron un modelo corpuscular que utiliza algún tipo de mecanismo de protección o sombreado. En 1784, Le Sage postuló que la gravedad podría ser resultado de la colisión de átomos y, a principios del siglo XIX, amplió la teoría de la presión corpuscular de Daniel Bernoulli al universo en su conjunto. Un modelo similar fue creado más tarde por Hendrik Lorentz (1853-1928), quien utilizó radiación electromagnética en lugar de corpúsculos.

El matemático inglés Isaac Newton utilizó el argumento de Descartes de que el movimiento curvilíneo limita la inercia y, en 1675, sostuvo que las corrientes de éter atraen a todos los cuerpos entre sí. Newton (1717) y Leonhard Euler (1760) propusieron un modelo en el que el éter pierde densidad cerca de la masa, lo que lleva a una fuerza neta que actúa sobre los cuerpos. Entre 1650 y 1900 se crearon otras explicaciones mecánicas de la gravitación (incluida la teoría de Le Sage) para explicar la teoría de Newton, pero los modelos mecanicistas finalmente cayeron en desgracia porque la mayoría de ellos conducen a una cantidad inaceptable de arrastre (resistencia del aire), que no se observaba. Otros violan la ley de conservación de la energía y son incompatibles con la termodinámica moderna.

Antes de Newton, "peso" tenía el doble significado de "cantidad" y "pesadez".

Lo que ahora sabemos como masa fue hasta el momento de Newton llamado “peso”.... Un orfebre creía que una onza de oro era una cantidad de oro.... Pero los antiguos creían que un equilibrio de haz también midió la “avidad” que reconocieron a través de sus sentidos musculares.... Se creía que la misa y su fuerza descendente asociada eran lo mismo. Kepler formó un concepto [distinto] de masa (“monto de la materia” (materia copiae)), pero lo llamó “peso” como todos en ese momento.

—K. M. Browne, El significado pre-Newtoniano de la palabra “peso”

En 1686, Newton dio nombre al concepto de masa. En el primer párrafo de los Principia, Newton definió la cantidad de materia como “densidad y volumen conjuntamente”, y la masa como cantidad de materia.

La cantidad de materia es la medida de lo mismo, derivada de su densidad y vracs conjuntamente... Es esta cantidad que me refiero en todas partes bajo el nombre del cuerpo o la masa. Y lo mismo es conocido por el peso de cada cuerpo; porque es proporcional al peso.

—Isaac Newton, Principios matemáticos de la filosofía natural, Definición I.

En 1679, Robert Hooke escribió a Isaac Newton sobre su hipótesis acerca del movimiento orbital, que depende en parte de una fuerza del cuadrado inverso. En 1684, tanto Hooke como Newton le dijeron a Edmond Halley que habían demostrado la ley del cuadrado inverso del movimiento planetario, en enero y agosto, respectivamente. Aunque Hooke se negó a presentar sus pruebas, Newton se sintió impulsado a componer De motu corporum in gyrum ('Sobre el movimiento de los cuerpos en una órbita'), en el que deduce matemáticamente las leyes de Kepler sobre el movimiento planetario. En 1687, con el apoyo de Halley (y para consternación de Hooke), Newton publicó Philosophiæ Naturalis Principia Mathematica (Principios matemáticos de la filosofía natural), que plantea la hipótesis de la ley del cuadrado inverso de la gravitación universal. En sus propias palabras:

Deduje que las fuerzas que mantienen a los planetas en sus orbes deben ser recíprocamente como los cuadrados de sus distancias de los centros sobre los que giran; y así comparar la fuerza necesaria para mantener la luna en su orbe con la fuerza de gravedad en la superficie de la tierra; y los halló para responder casi.

La fórmula original de Newton era:

${\fnMicrosoft {\fnMicrosoft Sans Serif}\fnMicroc {\fnMicrom {\,of\,object\,1\,\,\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans}}}} {\\\fnMicros}}\\\\\\\\\\\\\\\\\fnMicrom}\\\\fnMicrom}\\\\\\\\\\\\\\\\\\\\\fnMicrom\\\\\\\\\\\\\\\\\\\\\\\fnMicrom}\\\\\\\\\\\\\\\\\\\\\\\\\fnMicrox4\fnMicrox4\\\\\\\fnMicrom {distance\,from\,centers}}}$

donde el símbolo ${\displaystyle \propto }$ significa "es proporcional a". Para convertir esto en una fórmula o ecuación de la misma cara, debía haber un factor multiplicador o una constante que daría la fuerza correcta de la gravedad sin importar el valor de las masas o la distancia entre ellas – la constante gravitacional. Newton necesitaría una medida exacta de esta constante para probar su ley inversa-cuarela. Las mediciones razonablemente precisas no estaban disponibles hasta el experimento de Cavendish de Henry Cavendish en 1797.

En la teoría de Newton (reescrito usando matemáticas más modernas) la densidad de masa ${\displaystyle \rho \,}$ genera un campo de escalar, el potencial gravitacional ${\displaystyle \varphi \,}$ en joules por kilogramo, por

${\displaystyle {\partial ^{2}\varphi \over \partial x^{j}\,\partial x^{j}=4\pi G\rho \,$

Utilizando el operador Nabla ${\displaystyle \nabla }$ para el gradiente y la divergencia (dependientes parciales), esto se puede escribir convenientemente como:

${\displaystyle \nabla ^{2}\varphi =4\pi G\rho \,}$

Este campo escalar gobierna el movimiento de una partícula en caída libre mediante:

${\displaystyle {d^{2}x^{j} \over dt^{2}=-{\partial} \varphi \over \partial x^{j}\,}$

A una distancia r de una masa aislada M, el campo escalar es

${\displaystyle \varphi =-{\frac {GM}\,}$

Los Principia se agotaron rápidamente, lo que inspiró a Newton a publicar una segunda edición en 1713. Sin embargo, la teoría de la gravedad en sí no fue aceptada rápidamente.

La teoría de la gravedad se enfrentó a dos obstáculos. Primero, científicos como Gottfried Wilhelm Leibniz se quejaron de que dependía de la acción a distancia, de que el mecanismo de la gravedad era "invisible, intangible y no mecánico". El filósofo francés Voltaire refutó estas preocupaciones y, en 1738, escribió su propio libro para explicar aspectos de la teoría a los lectores franceses, lo que ayudó a popularizar la teoría de Newton.

En segundo lugar, las comparaciones detalladas con los datos astronómicos no fueron inicialmente favorables. Uno de los problemas más evidentes fue la llamada gran desigualdad de Júpiter y Saturno. Las comparaciones de las observaciones astronómicas antiguas con las de principios del siglo XVIII implicaban que la órbita de Saturno aumentaba de diámetro mientras que la de Júpiter disminuía. En última instancia, esto significaba que Saturno abandonaría el Sistema Solar y Júpiter colisionaría con otros planetas o con el Sol. El problema fue abordado primero por Leonhard Euler en 1748, luego por Joseph-Louis Lagrange en 1763 y por Pierre-Simon Laplace en 1773. Cada esfuerzo mejoró el tratamiento matemático hasta que Laplace resolvió el problema en 1784, aproximadamente 100 años después de la primera publicación de Newton sobre la gravedad. Laplace demostró que los cambios eran periódicos pero con períodos inmensamente largos más allá de cualquier medición existente.

Se fueron acumulando éxitos, como la solución al gran misterio de la desigualdad entre Júpiter y Saturno. En 1755, el filósofo prusiano Immanuel Kant publicó un manuscrito cosmológico basado en los principios newtonianos, en el que desarrolla una versión temprana de la hipótesis nebular. Edmond Halley propuso que los objetos de aspecto similar que aparecían cada 76 años eran en realidad un único cometa. La aparición del cometa en 1759, que ahora lleva su nombre, un mes después de las predicciones basadas en la gravedad de Newton, mejoró enormemente la opinión científica sobre la teoría. La teoría de Newton disfrutó de su mayor éxito cuando se utilizó para predecir la existencia de Neptuno basándose en los movimientos de Urano que no podían explicarse por las acciones de los otros planetas. Los cálculos de John Couch Adams y Urbain Le Verrier predijeron la posición general del planeta. En 1846, Le Verrier envió su posición a Johann Gottfried Galle, pidiéndole que la verificara. Esa misma noche, Galle avistó a Neptuno cerca de la posición que había predicho Le Verrier.

No todas las comparaciones resultaron acertadas. A finales del siglo XIX, Le Verrier demostró que la órbita de Mercurio no podía explicarse en su totalidad bajo la gravedad newtoniana, y todas las búsquedas de otro cuerpo perturbador (como un planeta que orbitara el Sol aún más cerca que Mercurio) resultaron infructuosas. Aun así, se cree que la teoría de Newton es excepcionalmente precisa en el límite de los campos gravitatorios débiles y las velocidades bajas.

A finales del siglo XIX, muchos intentaron combinar la ley de fuerza de Newton con las leyes establecidas de la electrodinámica (como las de Wilhelm Eduard Weber, Carl Friedrich Gauss y Bernhard Riemann) para explicar la precesión anómala del perihelio de Mercurio. En 1890, Maurice Lévy lo logró combinando las leyes de Weber y Riemann, según las cuales la velocidad de la gravedad es igual a la velocidad de la luz. En otro intento, Paul Gerber (1898) logró derivar la fórmula correcta para el desplazamiento del perihelio (que era idéntica a la fórmula utilizada posteriormente por Albert Einstein). Estas hipótesis fueron rechazadas debido a que las leyes en las que se basaban estaban obsoletas, y fueron reemplazadas por las de James Clerk Maxwell.

En 1900, Hendrik Lorentz intentó explicar la gravedad basándose en su teoría del éter y en las ecuaciones de Maxwell. Supuso, al igual que Ottaviano Fabrizio Mossotti y Johann Karl Friedrich Zöllner, que la atracción de partículas con cargas opuestas es más fuerte que la repulsión de partículas con cargas iguales. La fuerza neta resultante es exactamente lo que se conoce como gravitación universal, en la que la velocidad de la gravedad es la de la luz. Lorentz calculó que el valor del avance del perihelio de Mercurio era demasiado bajo.

A finales del siglo XIX, Lord Kelvin consideró la posibilidad de una teoría del todo. Propuso que todos los cuerpos pulsan, lo que podría ser una explicación de la gravitación y las cargas eléctricas. Sus ideas eran en gran medida mecanicistas y requerían la existencia del éter, que el experimento de Michelson-Morley no logró detectar en 1887. Esto, combinado con el principio de Mach, condujo a modelos gravitacionales que presentan la acción a distancia.

Albert Einstein desarrolló su revolucionaria teoría de la relatividad en artículos publicados en 1905 y 1915; estos dan cuenta de la precesión del perihelio de Mercurio. En 1914, Gunnar Nordström intentó unificar la gravedad y el electromagnetismo en su teoría de la gravitación en cinco dimensiones. La relatividad general se demostró en 1919, cuando Arthur Eddington observó un efecto de lente gravitacional alrededor de un eclipse solar, que coincidía con las ecuaciones de Einstein. Esto dio como resultado que la teoría de Einstein reemplazara a la física newtoniana. A partir de entonces, el matemático alemán Theodor Kaluza promovió la idea de la relatividad general con una quinta dimensión, que en 1921 el físico sueco Oskar Klein dio una interpretación física en una teoría de cuerdas prototípica, un posible modelo de gravedad cuántica y una teoría potencial del todo.

Las ecuaciones de campo de Einstein incluyen una constante cosmológica para explicar la supuesta estaticidad del universo. Sin embargo, Edwin Hubble observó en 1929 que el universo parece estar expandiéndose. En la década de 1930, Paul Dirac desarrolló la hipótesis de que la gravitación debería disminuir lenta y constantemente a lo largo de la historia del universo. Alan Guth y Alexei Starobinsky propusieron en 1980 que la inflación cósmica en el universo primitivo podría haber sido impulsada por un campo de presión negativa, un concepto que más tarde se acuñó como "energía oscura", que en 2013 se descubrió que constituía alrededor del 68,3% del universo primitivo.

En 1922, Jacobus Kapteyn propuso la existencia de materia oscura, una fuerza invisible que mueve las estrellas en las galaxias a velocidades superiores a las que permite la gravedad por sí sola. En 2013 se descubrió que constituía el 26,8% del universo primitivo. Junto con la energía oscura, la materia oscura es un caso atípico en la relatividad de Einstein, y una explicación de sus efectos aparentes es un requisito para una teoría del todo exitosa.

En 1957, Hermann Bondi propuso que la masa gravitacional negativa (combinada con la masa inercial negativa) cumpliría con el principio de equivalencia fuerte de la relatividad general y las leyes del movimiento de Newton. La prueba de Bondi arrojó soluciones sin singularidades para las ecuaciones de la relatividad.

Las primeras teorías de la gravedad intentaron explicar las órbitas planetarias (Newton) y órbitas más complicadas (p. ej., Lagrange). Luego vinieron los intentos fallidos de combinar la gravedad con las teorías ondulatorias o corpusculares de la gravedad. Todo el panorama de la física cambió con el descubrimiento de las transformaciones de Lorentz, y esto condujo a los intentos de reconciliarla con la gravedad. Al mismo tiempo, los físicos experimentales comenzaron a probar los fundamentos de la gravedad y la relatividad: la invariancia de Lorentz, la desviación gravitacional de la luz, el experimento de Eötvös. Estas consideraciones condujeron al desarrollo de la relatividad general y lo siguieron.

En 1905, Albert Einstein publicó una serie de artículos en los que estableció la teoría especial de la relatividad y el hecho de que la masa y la energía son equivalentes. En 1907, en lo que describió como "el pensamiento más feliz de mi vida", Einstein se dio cuenta de que alguien que está en caída libre no experimenta ningún campo gravitatorio. En otras palabras, la gravitación es exactamente equivalente a la aceleración.

La publicación en dos partes de Einstein en 1912 (y antes en 1908) es realmente importante sólo por razones históricas. Para entonces ya conocía el corrimiento al rojo gravitacional y la desviación de la luz. Se había dado cuenta de que las transformaciones de Lorentz no son de aplicación general, pero las mantuvo. La teoría establece que la velocidad de la luz es constante en el espacio libre pero varía en presencia de materia. Se esperaba que la teoría sólo fuera válida cuando la fuente del campo gravitacional estuviera estacionaria. Incluye el principio de mínima acción:

${\displaystyle \delta \int d\tau =0\,}$

${\displaystyle {d\tau }{2}=-\eta _{\mu\nu }\,dx^{\mu }\,dx^{\nu }\,}$

Donde ${\displaystyle \eta _{\mu\nu }\,}$ es la métrica de Minkowski, y hay una suma de 1 a 4 sobre índices ${\displaystyle \mu \,}$ y ${\displaystyle \nu \nu}$.

Einstein y Grossmann incluyen la geometría de Riemann y el cálculo tensorial.

${\displaystyle \delta \int d\tau =0\,}$

${\displaystyle {d\tau }{2}=-g_{\mu\nu }\,dx^{\mu }\,dx^{\nu }\,}$

Las ecuaciones de la electrodinámica coinciden exactamente con las de la relatividad general. La ecuación

${\displaystyle T^{\mu \nu }=\rho {dx^{\mu } \over d\tau }{dx^{\nu } \over d\tau }\,}$

No se encuentra en la relatividad general. Expresa el tensor de tensión-energía como una función de la densidad de materia.

Basándose en el principio de la relatividad, Henri Poincaré (1905, 1906), Hermann Minkowski (1908) y Arnold Sommerfeld (1910) intentaron modificar la teoría de Newton y establecer una ley gravitatoria invariante de Lorentz, en la que la velocidad de la gravedad es la de la luz. Como en el modelo de Lorentz, el valor del avance del perihelio de Mercurio era demasiado bajo.

Mientras tanto, Max Abraham desarrolló un modelo alternativo de la gravedad en el que la velocidad de la luz depende de la intensidad del campo gravitatorio y, por lo tanto, es variable en casi todas partes. Se dice que la revisión de los modelos gravitacionales que realizó Abraham en 1914 es excelente, pero su propio modelo era deficiente.

El primer enfoque de Nordström (1912) fue mantener la métrica de Minkowski y un valor constante de ${\displaystyle c\,}$ pero dejar que la masa dependa de la fuerza de campo gravitacional ${\displaystyle \varphi \,}$. Permitir esta fuerza de campo para satisfacer

${\displaystyle \Box \varphi =\rho \,}$

Donde ${\displaystyle \rho \,}$ es energía de masa de descanso y ${\displaystyle \Box \,}$ es el d'Alembertian,

${\displaystyle m=m_{0}\exp \left({\frac {\varphi ¿Qué? }$

Donde ${\displaystyle m_{0}$ es la masa cuando el potencial gravitacional desaparece y,

${\displaystyle -{\partial \varphi \over \partial x^{\mu }={\dot {u}_{\mu} }+{u_{\mu } \over c^{2}{\dot {\varphi ♪♪$

Donde ${\displaystyle u\,}$ es la cuatro-velocidad y el punto es un diferencial con respecto al tiempo.

El segundo enfoque de Nordström (1913) se recuerda como la primera teoría relativista de la gravitación de campo lógicamente consistente jamás formulada. (Notación de Pais, no de Nordström):

${\displaystyle \delta \int \psi \,d\tau =0\,}$

${\displaystyle {d\tau }{2}=-\eta _{\mu\nu }\,dx^{\mu }\,dx^{\nu }\,}$

Donde ${\displaystyle \psi \,}$ es un campo de escalar,

${\displaystyle - {\partial T^{\mu\nu } \over \partial x^{\nu }=T{1 \over \psi }{\partial \psi \over \partial x_{\mu }\,}$

Esta teoría es invariante respecto de Lorentz, satisface las leyes de conservación, se reduce correctamente al límite newtoniano y satisface el principio de equivalencia débil.

Esta teoría es el primer análisis de Einstein de la gravitación en el que se respeta estrictamente la covarianza general. Escritura:

${\displaystyle \delta \int ds=0\,}$

${\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif}$

${\displaystyle g_{\mu\nu }=\psi ^{2}\eta _{\mu\nu }\,}$

Relacionan a Einstein-Grossmann con Nordström. También afirman:

${\displaystyle T\,\propto \,R\,.}$

Es decir, la traza del tensor de energía de tensión es proporcional a la curvatura del espacio.

Entre 1911 y 1915, Einstein desarrolló la idea de que la gravitación es equivalente a la aceleración, inicialmente enunciada como principio de equivalencia, en su teoría general de la relatividad, que fusiona las tres dimensiones del espacio y la única dimensión del tiempo en el tejido cuatridimensional del espacio-tiempo. Sin embargo, no unifica la gravedad con los cuantos, partículas individuales de energía, cuya existencia el propio Einstein había postulado en 1905.

En la relatividad general, los efectos de la gravitación se atribuyen a la curvatura del espacio-tiempo en lugar de a una fuerza. El punto de partida de la relatividad general es el principio de equivalencia, que equipara la caída libre con el movimiento inercial. El problema que esto crea es que los objetos en caída libre pueden acelerarse unos con respecto a otros. Para abordar esta dificultad, Einstein propuso que el espacio-tiempo está curvado por la materia y que los objetos en caída libre se mueven a lo largo de trayectorias localmente rectas en el espacio-tiempo curvado. Más específicamente, Einstein y David Hilbert descubrieron las ecuaciones de campo de la relatividad general, que relacionan la presencia de materia y la curvatura del espacio-tiempo. Estas ecuaciones de campo son un conjunto de 10 ecuaciones diferenciales simultáneas, no lineales. Las soluciones de las ecuaciones de campo son los componentes del tensor métrico del espacio-tiempo, que describe su geometría. Las trayectorias geodésicas del espacio-tiempo se calculan a partir del tensor métrico.

Entre las soluciones más destacadas de las ecuaciones de campo de Einstein se incluyen:

• La solución Schwarzschild, que describe el tiempo espacial que rodea un objeto masivo sin carga esféricamente simétrico. Para objetos con radio más pequeño que el radio Schwarzschild, esta solución genera un agujero negro con una singularidad central.
• La solución Reissner-Nordström, en la que el objeto central tiene una carga eléctrica. Para cargos con una longitud geometrizada inferior a la longitud geometrizada de la masa del objeto, esta solución produce agujeros negros con un horizonte de eventos que rodea un horizonte Cauchy.
• La solución Kerr para rotar objetos masivos. Esta solución también produce agujeros negros con múltiples horizontes.
• La solución cosmológica Robertson-Walker (de 1922 y 1924), que predice la expansión del universo.

La relatividad general ha tenido mucho éxito porque sus predicciones (que no exigían las teorías de la gravedad anteriores) se han confirmado con regularidad. Por ejemplo:

• La relatividad general representa la precesión anómala del perhelio de Mercurio.
• La lente gravitacional fue confirmada por primera vez en 1919, y ha sido confirmada más recientemente a través del uso de un quásar que pasa detrás del Sol como se ve desde la Tierra.
• La expansión del universo (predictada por la métrica Robertson-Walker) fue confirmada por Edwin Hubble en 1929.
• La predicción de que el tiempo corre más lento a los potenciales más bajos ha sido confirmada por el experimento Pound-Rebka, el experimento Hafele–Keating y el GPS.
• El retraso de la luz que pasa cerca de un objeto masivo fue identificado por primera vez por Irwin Shapiro en 1964 en señales de naves espaciales interplanetarias.
• La radiación gravitacional ha sido confirmada indirectamente a través de estudios de pulsares binarios como PSR 1913+16.
  • En 2015, el LIGO experimentó directamente la radiación gravitacional detectada a partir de dos agujeros negros colliding, haciendo de esta la primera observación directa de ondas gravitacionales y agujeros negros.

Se cree que las fusiones de estrellas de neutrones (detectadas desde 2017) y la formación de agujeros negros también pueden crear cantidades detectables de radiación gravitacional.

Varias décadas después del descubrimiento de la relatividad general, se comprendió que no puede ser la teoría completa de la gravedad porque es incompatible con la mecánica cuántica. Más tarde se entendió que es posible describir la gravedad en el marco de la teoría cuántica de campos como las otras fuerzas fundamentales. En este marco, la fuerza de atracción de la gravedad surge debido al intercambio de gravitones virtuales, de la misma manera que la fuerza electromagnética surge del intercambio de fotones virtuales. Esto reproduce la relatividad general en el límite clásico, pero solo en el nivel linealizado y postulando que se cumplen las condiciones para la aplicabilidad del teorema de Ehrenfest, lo que no siempre es el caso. Además, este enfoque falla a distancias cortas del orden de la longitud de Planck.

• Antigravidad
• Historia de la física

• Gillispie, Charles Coulston (1960). El borde de la objetividad: Un ensayo en la historia de las ideas científicas. Princeton University Press. ISBN 0-691-02350-6.
• Wallace, W. A. (2004a). "El enigma de Domingo de Soto: Uniformiter difformis y cuerpos caídos en la física medieval tardía". En Wallace, W. A. (ed.). Domingo de Soto y el Galileo temprano: Ensayos sobre la historia intelectual. Routledge. (Reimpreso de "El enigma de Domingo de Soto: Uniformiter difformis y cuerpos caídos en la física medieval tardía". (1968). Isis, 59(4), 384–401).
• Wallace, W. A. (2004b). "Domingo de Soto y las raíces ibéricas de la ciencia de Galileo". En Wallace, W. A. (ed.). Domingo de Soto y el Galileo temprano: Ensayos sobre la historia intelectual. Routledge. (Reimpreso de White, K. (Ed. (1997)). Filosofía hispana en la era del descubrimiento. Estudios en Filosofía e Historia de la Filosofía 29. Catholic University of America Press).