Hipótesis nula

En estadística inferencial una hipótesis nula (H₀) significa que dos posibilidades diferentes son exactamente iguales. Es decir, la hipótesis nula es un planteamiento hipotético que no representa ninguna variación probabilística, donde por tanto cualquier diferencia observada se debe únicamente al azar. Usando pruebas estadísticas, es posible calcular la probabilidad de que la hipótesis nula sea cierta.

Definiciones básicas

La hipótesis nula y la hipótesis alternativa son tipos de conjeturas utilizadas en pruebas estadísticas, que son métodos formales para llegar a conclusiones o tomar decisiones sobre la base de datos. Las hipótesis son conjeturas sobre un modelo estadístico de la población, que se basan en una muestra de la población. Las pruebas son elementos centrales de la inferencia estadística, muy utilizados en la interpretación de datos experimentales científicos, para separar las afirmaciones científicas del ruido estadístico.

"La declaración que se prueba en una prueba de significancia estadística se denomina hipótesis nula. La prueba de significancia está diseñada para evaluar la fuerza de la evidencia contra la hipótesis nula. Por lo general, la hipótesis nula es una declaración de 'sin efecto' o ' ninguna diferencia'." A menudo se simboliza como H ₀.

El enunciado que se contrasta con la hipótesis nula es la hipótesis alternativa. Los símbolos incluyen H ₁ y H _a.

Prueba de significancia estadística: "En términos generales, el procedimiento para decidir es así: tome una muestra aleatoria de la población. Si los datos de la muestra son consistentes con la hipótesis nula, entonces no rechace la hipótesis nula; si los datos de la muestra son inconsistentes con la hipótesis nula". la hipótesis nula, luego rechace la hipótesis nula y concluya que la hipótesis alternativa es verdadera".

Lo siguiente agrega contexto y matiz a las definiciones básicas.

Dados los puntajes de las pruebas de dos muestras aleatorias, una de hombres y otra de mujeres, ¿diferencia un grupo del otro? Una posible hipótesis nula es que la puntuación media de los hombres es la misma que la puntuación media de las mujeres:H ₀: μ ₁ = μ ₂

dondeH ₀ = la hipótesis nula,μ ₁ = la media de la población 1, yμ ₂ = la media de la población 2.

Una hipótesis nula más sólida es que las dos muestras se extraen de la misma población, de modo que las varianzas y las formas de las distribuciones también son iguales.

Terminología

Hipótesis simpleCualquier hipótesis que especifique completamente la distribución de la población. Para tal hipótesis, la distribución muestral de cualquier estadística es una función únicamente del tamaño de la muestra.Hipótesis compuestaCualquier hipótesis que no especifique completamente la distribución de la población. Ejemplo: una hipótesis que especifica una distribución normal con una media especificada y una varianza no especificada.

La distinción simple/compuesto fue realizada por Neyman y Pearson.Hipótesis exactaCualquier hipótesis que especifica un valor de parámetro exacto. Ejemplo: μ = 100. Sinónimo: hipótesis puntual.Hipótesis inexactaLos que especifican un rango o intervalo de parámetros. Ejemplos: μ ≤ 100; 95 ≤ μ ≤ 105.

Fisher requirió una hipótesis nula exacta para la prueba (ver las citas a continuación).

Una hipótesis de una cola (probada mediante una prueba de una cola) es una hipótesis inexacta en la que el valor de un parámetro se especifica como:

• superior o igual a cierto valor, o
• inferior o igual a un valor determinado.

Se dice que una hipótesis de una cola tiene direccionalidad.

El ejemplo original de Fisher (dama probando té) era una prueba de una cola. La hipótesis nula era asimétrica. La probabilidad de adivinar todas las tazas correctamente era la misma que la de adivinar todas las tazas incorrectamente, pero Fisher notó que solo adivinar correctamente era compatible con la afirmación de la dama.

Ejemplos

• ¿Son los niños más altos que las niñas a los ocho años? La hipótesis nula es "tienen la misma estatura promedio".
• ¿Los adolescentes usan las aplicaciones de localización de restaurantes más que los adultos? La hipótesis nula es "usan estas aplicaciones la misma cantidad promedio".
• ¿Comer una manzana al día reduce las visitas al médico? La hipótesis nula es "las manzanas no reducen las visitas al médico".
• ¿Son los estados pequeños más densamente poblados que los estados grandes? La hipótesis nula es que "los estados pequeños tienen la misma densidad de población que los estados grandes".
• ¿Los estados grandes están más densamente poblados que los estados pequeños? La hipótesis nula es que "los estados grandes tienen la misma densidad de población que los estados pequeños".
• ¿El tamaño de un estado afecta la densidad de población? La hipótesis nula es "todos los estados tienen la misma densidad de población".
• ¿Los perros grandes prefieren las croquetas grandes? La hipótesis nula es que "los perros grandes no tienen preferencia por croquetas grandes".
• ¿Los gatos prefieren pescado o leche? La hipótesis nula es "los gatos no tienen preferencias, les gustan igual".

Descripción técnica

La hipótesis nula es una hipótesis por defecto de que una cantidad a medir es cero (nula). Normalmente, la cantidad a medir es la diferencia entre dos situaciones. Por ejemplo, tratar de determinar si existe una prueba positiva de que se ha producido un efecto o que las muestras proceden de diferentes lotes.

La hipótesis nula establece que una cantidad (de interés) es mayor o igual a cero y menor o igual a cero. Si cualquiera de los requisitos puede anularse positivamente, la hipótesis nula está "excluida del ámbito de las posibilidades".

En general, se supone que la hipótesis nula sigue siendo posiblemente cierta. Se pueden realizar múltiples análisis para mostrar cómo se debe rechazar o excluir la hipótesis, por ejemplo, si tiene un alto nivel de confianza, lo que demuestra una diferencia estadísticamente significativa. Esto se demuestra al mostrar que el cero está fuera del intervalo de confianza especificado de la medición en cualquier lado, generalmente dentro de los números reales. El hecho de no excluir la hipótesis nula (con alguna confianza) no confirma ni respalda lógicamente la hipótesis nula (no demostrable). (Cuando se prueba que algo es, por ejemplo, mayor que x, no implica necesariamente que sea plausible que sea menor o igual que x; en cambio, puede ser una medición de mala calidad con baja precisión. Confirmar la hipótesis nula de dos colas equivaldría a probar positivamente que es mayor o igual que 0 ya probar positivamente que es menor o igual a 0; esto es algo para lo que se necesita una precisión infinita, así como un efecto exactamente nulo, ninguno de los cuales normalmente es realista. Además, las mediciones nunca indicarán una probabilidad distinta de cero de una diferencia exactamente cero). Por lo tanto, el fracaso de una exclusión de una hipótesis nula equivale a un "no sé" en el nivel de confianza especificado; no implica inmediatamente nulo de alguna manera, ya que los datos ya pueden mostrar una indicación (menos fuerte) de no nulo. El nivel de confianza utilizado ciertamente no corresponde a la probabilidad de nulo al no poder excluir; de hecho, en este caso, un alto nivel de confianza utilizado amplía el rango aún plausible.

Una hipótesis no nula puede tener los siguientes significados, dependiendo del autor a) se utiliza un valor distinto de cero, b) se utiliza algún margen distinto de cero y c) la hipótesis "alternativa".

Probar (excluir o no excluir) la hipótesis nula proporciona evidencia de que hay (o no hay) motivos estadísticamente suficientes para creer que existe una relación entre dos fenómenos (p. ej., que un tratamiento potencial tiene un efecto distinto de cero, de cualquier manera). Probar la hipótesis nula es una tarea central en la prueba de hipótesis estadísticas en la práctica moderna de la ciencia. Existen criterios precisos para excluir o no excluir una hipótesis nula en un cierto nivel de confianza. El nivel de confianza debe indicar la probabilidad de que muchos más y mejores datos aún puedan excluir la hipótesis nula del mismo lado.

El concepto de hipótesis nula se usa de manera diferente en dos enfoques de la inferencia estadística. En el enfoque de prueba de significación de Ronald Fisher, se rechaza una hipótesis nula si es muy poco probable que los datos observados se hayan producido si la hipótesis nula fuera verdadera. En este caso, se rechaza la hipótesis nula y se acepta una hipótesis alternativa en su lugar. Si los datos son consistentes con la hipótesis nula estadísticamente posiblemente verdadera, entonces la hipótesis nula no se rechaza. En ningún caso se prueba la hipótesis nula o su alternativa; con mejores o más datos, el nulo aún puede ser rechazado. Esto es análogo al principio legal de presunción de inocencia,

En el enfoque de prueba de hipótesis de Jerzy Neyman y Egon Pearson, una hipótesis nula se contrasta con una hipótesis alternativa, y las dos hipótesis se distinguen sobre la base de los datos, con ciertas tasas de error. Se utiliza en la formulación de respuestas en la investigación.

La inferencia estadística se puede realizar sin una hipótesis nula, especificando un modelo estadístico correspondiente a cada hipótesis candidata y utilizando técnicas de selección de modelos para elegir el modelo más apropiado. (Las técnicas de selección más comunes se basan en el criterio de información de Akaike o en el factor de Bayes).

Principio

La prueba de hipótesis requiere la construcción de un modelo estadístico de cómo se verían los datos si el azar o los procesos aleatorios fueran los únicos responsables de los resultados. La hipótesis de que sólo el azar es responsable de los resultados se llama hipótesis nula. El modelo del resultado del proceso aleatorio se denomina distribución bajo la hipótesis nula. Los resultados obtenidos se comparan con la distribución bajo la hipótesis nula, y así se determina la probabilidad de encontrar los resultados obtenidos.

La prueba de hipótesis funciona mediante la recopilación de datos y la medición de la probabilidad de que el conjunto de datos en particular sea (suponiendo que la hipótesis nula sea verdadera), cuando el estudio se realiza en una muestra representativa seleccionada al azar. La hipótesis nula supone que no hay relación entre las variables de la población de la que se selecciona la muestra.

Si el conjunto de datos de una muestra representativa seleccionada al azar es muy poco probable en relación con la hipótesis nula (definida como parte de una clase de conjuntos de datos que rara vez se observarán), el experimentador rechaza la hipótesis nula, concluyéndola (probablemente) Es falso. Esta clase de conjuntos de datos generalmente se especifica a través de una estadística de prueba, que está diseñada para medir el grado de desviación aparente de la hipótesis nula. El procedimiento funciona evaluando si la desviación observada, medida por el estadístico de prueba, es mayor que un valor definido, de modo que la probabilidad de ocurrencia de un valor más extremo sea pequeña bajo la hipótesis nula (generalmente en menos del 5% o 1 % de conjuntos de datos similares en los que se cumple la hipótesis nula).

Si los datos no contradicen la hipótesis nula, entonces solo se puede llegar a una conclusión débil: a saber, que el conjunto de datos observado proporciona evidencia insuficiente contra la hipótesis nula. En este caso, debido a que la hipótesis nula puede ser verdadera o falsa, en algunos contextos esto se interpreta como que los datos proporcionan evidencia insuficiente para llegar a una conclusión, mientras que en otros contextos se interpreta como que no hay evidencia suficiente para llegar a una conclusión. apoyar el cambio de un régimen actualmente útil a otro diferente. Sin embargo, si en este punto el efecto parece probable y/o lo suficientemente grande, puede haber un incentivo para investigar más a fondo, como analizar una muestra más grande.

Por ejemplo, cierto medicamento puede reducir la posibilidad de sufrir un ataque al corazón. Las posibles hipótesis nulas son "este fármaco no reduce las posibilidades de sufrir un infarto" o "este fármaco no tiene ningún efecto sobre las posibilidades de sufrir un infarto". La prueba de la hipótesis consiste en administrar el fármaco a la mitad de las personas de un grupo de estudio a modo de experimento controlado. Si los datos muestran un cambio estadísticamente significativo en las personas que reciben el fármaco, se rechaza la hipótesis nula.

Objetivos de las pruebas de hipótesis nula

Existen muchos tipos de pruebas de significación para una, dos o más muestras, para medias, varianzas y proporciones, datos apareados o no apareados, para diferentes distribuciones, para muestras grandes y pequeñas; todos tienen hipótesis nulas. También hay al menos cuatro objetivos de hipótesis nulas para las pruebas de significación:

• Las hipótesis nulas técnicas se utilizan para verificar los supuestos estadísticos. Por ejemplo, los residuos entre los datos y un modelo estadístico no se pueden distinguir del ruido aleatorio. Si es cierto, no hay justificación para complicar el modelo.
• Los supuestos científicos nulos se utilizan para avanzar directamente en una teoría. Por ejemplo, el momento angular del universo es cero. Si no es cierto, la teoría del universo primitivo puede necesitar una revisión.
• Se utilizan hipótesis nulas de homogeneidad para verificar que múltiples experimentos están produciendo resultados consistentes. Por ejemplo, el efecto de un medicamento en los ancianos es consistente con el de la población adulta en general. Si es cierto, esto fortalece la conclusión de efectividad general y simplifica las recomendaciones de uso.
• Las hipótesis nulas que afirman la igualdad de efecto de dos o más tratamientos alternativos, por ejemplo, un fármaco y un placebo, se utilizan para reducir las afirmaciones científicas basadas en ruido estadístico. Esta es la hipótesis nula más popular; Es tan popular que muchas declaraciones sobre pruebas significativas asumen tales hipótesis nulas.

El rechazo de la hipótesis nula no es necesariamente el objetivo real de un probador de significación. Un modelo estadístico adecuado puede estar asociado con una falla en rechazar el valor nulo; el modelo se ajusta hasta que no se rechaza el nulo. Fisher conocía bien los numerosos usos de las pruebas de significación, y discutió muchos en su libro escrito una década antes de definir la hipótesis nula.

Una prueba de significancia estadística comparte muchas matemáticas con un intervalo de confianza. Se iluminan mutuamente. Un resultado suele ser significativo cuando hay confianza en el signo de una relación (el intervalo no incluye el 0). Siempre que el signo de una relación es importante, la significación estadística es un objetivo valioso. Esto también revela las debilidades de las pruebas de significación: un resultado puede ser significativo sin una buena estimación de la fuerza de una relación; la importancia puede ser una meta modesta. Una relación débil también puede lograr significación con suficientes datos. Comúnmente se recomienda informar tanto la importancia como los intervalos de confianza.

Los variados usos de las pruebas de significación reducen el número de generalizaciones que se pueden hacer sobre todas las aplicaciones.

Elección de la hipótesis nula

La elección de la hipótesis nula está asociada con consejos escasos e inconsistentes. Fisher mencionó algunas limitaciones en la elección y afirmó que se deben considerar muchas hipótesis nulas y que son posibles muchas pruebas para cada una. La variedad de aplicaciones y la diversidad de objetivos sugiere que la elección puede ser complicada. En muchas aplicaciones la formulación de la prueba es tradicional. Una familiaridad con la gama de pruebas disponibles puede sugerir una hipótesis y una prueba nulas particulares. La formulación de la hipótesis nula no está automatizada (aunque los cálculos de las pruebas de significación suelen estarlo). Sir David Cox dijo: "La forma en que [la] traducción del problema de la materia en cuestión se realiza a un modelo estadístico es a menudo la parte más crítica de un análisis".

Una prueba de significación estadística está destinada a probar una hipótesis. Si la hipótesis resume un conjunto de datos, no tiene valor probar la hipótesis en ese conjunto de datos. Ejemplo: si un estudio de los informes meteorológicos del año pasado indica que la lluvia en una región cae principalmente los fines de semana, solo es válido probar esa hipótesis nula en los informes meteorológicos de cualquier otro año. Probar las hipótesis sugeridas por los datos es un razonamiento circular que no prueba nada; Es una limitación especial en la elección de la hipótesis nula.

Un procedimiento de rutina es el siguiente: Partir de la hipótesis científica. Traduzca esto a una hipótesis alternativa estadística y proceda: "Debido a que H _a expresa el efecto para el que deseamos encontrar evidencia, a menudo comenzamos con H _a y luego establecemos H ₀ como la afirmación de que el efecto esperado no está presente. " Este consejo se invierte para aplicaciones de modelado en las que esperamos no encontrar evidencia contra el nulo.

Un ejemplo de caso complejo es el siguiente: El estándar de oro en la investigación clínica es el ensayo clínico aleatorizado, doble ciego, controlado con placebo. Pero probar un nuevo fármaco contra un placebo (médicamente ineficaz) puede no ser ético para una enfermedad grave. Probar un fármaco nuevo frente a un fármaco médicamente eficaz más antiguo plantea cuestiones filosóficas fundamentales con respecto al objetivo de la prueba y la motivación de los experimentadores. La hipótesis nula estándar de "sin diferencia" puede recompensar a la compañía farmacéutica por recopilar datos inadecuados. La "diferencia" es una mejor hipótesis nula en este caso, pero la significación estadística no es un criterio adecuado para llegar a una conclusión matizada que requiere una buena estimación numérica de la eficacia del fármaco. Un "menor" o "simple"

Direccionalidad

La elección de la hipótesis nula (H ₀) y la consideración de la direccionalidad (ver "prueba de una cola") es fundamental.

Cola de la prueba de hipótesis nula

Considere la cuestión de si una moneda lanzada al aire es justa (es decir, que en promedio cae cara el 50% de las veces) y un experimento en el que lanza la moneda 5 veces. Un posible resultado del experimento que consideramos aquí es 5 cabezas. Deje que los resultados se consideren improbables con respecto a una distribución supuesta si su probabilidad es inferior a un umbral de significación de 0,05.

Una hipótesis nula potencial que implica una prueba de una cola es "esta moneda no está sesgada hacia las caras". Tenga en cuenta que, en este contexto, la palabra "cola" tiene dos significados: como resultado de un solo lanzamiento o como región de valores extremos en una distribución de probabilidad.

De hecho, con una moneda justa, la probabilidad del resultado de este experimento es 1/2 = 0,031, que sería incluso menor si la moneda estuviera sesgada a favor de las cruces. Por lo tanto, las observaciones no son lo suficientemente probables como para que se cumpla la hipótesis nula, y la prueba la refuta. Dado que la moneda aparentemente no es justa ni está sesgada hacia la cruz, la conclusión del experimento es que la moneda está sesgada hacia la cara.

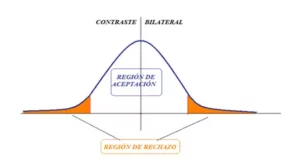
Alternativamente, una hipótesis nula que implica una prueba de dos colas es "esta moneda es justa". Esta única hipótesis nula podría examinarse buscando demasiadas cruces o demasiadas caras en los experimentos. Los resultados que tenderían a rechazar esta hipótesis nula son aquellos con un gran número de caras o un gran número de cruces, y nuestro experimento con 5 caras parecería pertenecer a esta clase.

Sin embargo, la probabilidad de 5 lanzamientos del mismo tipo, independientemente de si estos son cara o cruz, es el doble que la ocurrencia de 5 caras consideradas individualmente. Por lo tanto, bajo esta hipótesis nula de dos colas, la observación recibe un valor de probabilidad de 0,063. Por lo tanto, nuevamente, con el mismo umbral de significancia utilizado para la prueba de una cola (0.05), el mismo resultado no es estadísticamente significativo. Por lo tanto, la hipótesis nula de dos colas se mantendrá en este caso, no apoyando la conclusión alcanzada con la hipótesis nula de una sola cola, que la moneda está sesgada hacia cara.

Este ejemplo ilustra que la conclusión a la que se llega a partir de una prueba estadística puede depender de la formulación precisa de las hipótesis nula y alternativa.

Discusión

Fisher dijo, "la hipótesis nula debe ser exacta, es decir, libre de vaguedad y ambigüedad, porque debe proporcionar la base del 'problema de distribución', cuya solución es la prueba de significación", lo que implica un dominio más restrictivo para H ₀. De acuerdo con este punto de vista, la hipótesis nula debe ser numéricamente exacta: debe establecer que una cantidad o diferencia en particular es igual a un número en particular. En la ciencia clásica, lo más típico es la declaración de que no hay efecto de un tratamiento en particular; en las observaciones, normalmente no hay diferencia entre el valor de una variable medida en particular y el de una predicción.

La mayoría de los estadísticos creen que es válido establecer la dirección como parte de la hipótesis nula, o como parte de un par de hipótesis nula/hipótesis alternativa. Sin embargo, los resultados no son una descripción completa de todos los resultados de un experimento, sino simplemente un único resultado adaptado a un propósito particular. Por ejemplo, considere una H ₀ que afirma que la media poblacional de un nuevo tratamiento es una mejora en un tratamiento bien establecido con una media poblacional = 10 (conocida por una larga experiencia), siendo la alternativa de una cola que la media del nuevo tratamiento > 10 _ Si la evidencia muestral obtenida a través de x-bar es igual a −200 y el estadístico de prueba t correspondiente es igual a −50, la conclusión de la prueba sería que no hay evidencia de que el nuevo tratamiento sea mejor que el existente: no informaría que es notablemente peor, pero eso no es lo que busca esta prueba en particular. Para superar cualquier posible ambigüedad al informar el resultado de la prueba de una hipótesis nula, es mejor indicar si la prueba fue bilateral y, si fue unilateral, incluir la dirección del efecto que se está probando.

La teoría estadística requerida para tratar los casos simples de direccionalidad tratados aquí, y los más complicados, hace uso del concepto de prueba imparcial.

La direccionalidad de las hipótesis no siempre es obvia. La hipótesis nula explícita del ejemplo de Fisher's Lady probando té era que Lady no tenía tal habilidad, lo que condujo a una distribución de probabilidad simétrica. La naturaleza de una cola de la prueba resultó de la hipótesis alternativa de una cola (un término no utilizado por Fisher). La hipótesis nula se convirtió implícitamente en una cola. La negación lógica del reclamo unilateral de la Dama también fue unilateral. (Afirmación: Habilidad > 0; Nulo declarado: Habilidad = 0; Nulo implícito: Habilidad ≤ 0).

Los argumentos puros sobre el uso de pruebas de una cola se complican por la variedad de pruebas. Algunas pruebas (por ejemplo, la prueba de bondad de ajuste χ) son inherentemente unilaterales. Algunas distribuciones de probabilidad son asimétricas. Las pruebas tradicionales de 3 o más grupos son de dos colas.

Los consejos sobre el uso de hipótesis unilaterales han sido inconsistentes y la práctica aceptada varía entre los campos. La mayor objeción a las hipótesis unilaterales es su subjetividad potencial. Un resultado no significativo a veces se puede convertir en un resultado significativo mediante el uso de una hipótesis unilateral (como la prueba de la moneda justa, a capricho del analista). La otra cara del argumento: es menos probable que las pruebas unilaterales ignoren un efecto real. Las pruebas de una cola pueden suprimir la publicación de datos que difieren en signo de las predicciones. La objetividad era una meta de los desarrolladores de pruebas estadísticas.

Es una práctica común usar una hipótesis de una cola por defecto. Sin embargo, "si no tiene una dirección específica firmemente en mente de antemano, use una alternativa de dos lados. Además, algunos usuarios de estadísticas argumentan que siempre debemos trabajar con la alternativa de dos lados".

Una alternativa a este consejo es utilizar pruebas de tres resultados. Elimina los problemas relacionados con la direccionalidad de las hipótesis probando dos veces, una en cada dirección y combinando los resultados para producir tres resultados posibles. Las variaciones de este enfoque tienen una historia, siendo sugeridas quizás 10 veces desde 1950.

Los desacuerdos sobre las pruebas de una cola surgen de la filosofía de la ciencia. Si bien Fisher estaba dispuesto a ignorar el improbable caso de que la Dama adivinara incorrectamente todas las tazas de té (lo que puede haber sido apropiado para las circunstancias), la medicina cree que un tratamiento propuesto que mata a los pacientes es significativo en todos los sentidos y debería informarse y tal vez explicarse.. Las malas prácticas de informes estadísticos han contribuido a los desacuerdos sobre las pruebas de una cola. La significación estadística resultante de las pruebas de dos colas es insensible al signo de la relación; Informar la importancia por sí sola es inadecuado. "El tratamiento tiene un efecto" es el resultado no informativo de una prueba de dos colas. "El tratamiento tiene un efecto beneficioso" es el resultado más informativo de una prueba de una cola. "El tratamiento tiene un efecto, combinar el resultado de una prueba de significación de dos colas con una estimación numérica de la relación entre el tratamiento y el efecto. Informar explícitamente un resultado numérico elimina una ventaja filosófica de una prueba de una cola. Una cuestión subyacente es la forma apropiada de una ciencia experimental sin teorías predictivas numéricas: un modelo de resultados numéricos es más informativo que un modelo de signos de efecto (positivo, negativo o desconocido), que es más informativo que un modelo de significado simple (no cero o desconocido); en ausencia de teoría numérica, los signos pueden ser suficientes. combinar el resultado de una prueba de significación de dos colas con una estimación numérica de la relación entre el tratamiento y el efecto. Informar explícitamente un resultado numérico elimina una ventaja filosófica de una prueba de una cola. Una cuestión subyacente es la forma apropiada de una ciencia experimental sin teorías predictivas numéricas: un modelo de resultados numéricos es más informativo que un modelo de signos de efecto (positivo, negativo o desconocido), que es más informativo que un modelo de significado simple (no cero o desconocido); en ausencia de teoría numérica, los signos pueden ser suficientes. Un modelo de resultados numéricos es más informativo que un modelo de signos de efecto (positivo, negativo o desconocido) que es más informativo que un modelo de significado simple (distinto de cero o desconocido); en ausencia de teoría numérica, los signos pueden ser suficientes. Un modelo de resultados numéricos es más informativo que un modelo de signos de efecto (positivo, negativo o desconocido) que es más informativo que un modelo de significado simple (distinto de cero o desconocido); en ausencia de teoría numérica, los signos pueden ser suficientes.

Historia de las pruebas estadísticas

La historia de las hipótesis nula y alternativa está incrustada en la historia de las pruebas estadísticas.

• Antes de 1925: hay rastros transitorios ocasionales de pruebas estadísticas durante siglos en el pasado, que proporcionan ejemplos tempranos de hipótesis nulas. A finales del siglo XIX se definió la significación estadística. A principios del siglo XX se definieron importantes distribuciones de probabilidad. Gossett y Pearson trabajaron en casos específicos de pruebas de significación.
• 1925: Fisher publicó la primera edición de Statistical Methods for Research Workers, que definió la prueba de significación estadística y la convirtió en un método de análisis principal para gran parte de la ciencia experimental. El texto estaba desprovisto de pruebas y débil en las explicaciones, pero estaba lleno de ejemplos reales. Colocó la práctica estadística en las ciencias mucho antes de la teoría estadística publicada.
• 1933: en una serie de artículos (publicados durante una década a partir de 1928), Neyman & Pearson definieron la prueba de hipótesis estadística como una propuesta de mejora de la prueba de Fisher. Los documentos proporcionaron gran parte de la terminología para las pruebas estadísticas, incluida la hipótesis alternativa y H ₀ como hipótesis para ser probada utilizando datos de observación (con H ₁, H ₂... como alternativas). Neyman no usó el término hipótesis nula en escritos posteriores sobre su método.
• 1935: Fisher publicó la primera edición del libro El diseño de experimentos que introdujo la hipótesis nula (por ejemplo más que por definición) y explicó cuidadosamente la justificación de las pruebas de significación en el contexto de la interpretación de los resultados experimentales; ver El diseño de experimentos # Citas con respecto a la hipótesis nula.
• Siguiente: Fisher y Neyman discutieron sobre los méritos relativos de sus formulaciones en competencia hasta la muerte de Fisher en 1962. Los cambios de carrera y la Segunda Guerra Mundial terminaron con la asociación de Neyman y Pearson. Las formulaciones fueron fusionadas por escritores de libros de texto, experimentadores (editores de revistas) y estadísticos matemáticos relativamente anónimos sin la participación de los directores. El tema de hoy combina gran parte de la terminología y el poder explicativo de Neyman & Pearson con la filosofía científica y los cálculos proporcionados por Fisher. Si las pruebas estadísticas son propiamente un tema o dos sigue siendo una fuente de desacuerdo. Muestra de dos: un texto se refiere al tema como prueba de hipótesis (sin mencionar la prueba de significación en el índice), mientras que otro dice prueba de significación (con una sección sobre la inferencia como decisión). Fisher desarrolló pruebas de significancia como una herramienta flexible para que los investigadores sopesen su evidencia. En cambio, las pruebas se han institucionalizado. La significación estadística se ha convertido en un criterio rígidamente definido y aplicado para la publicación de resultados experimentales en muchas revistas científicas. En algunos campos, las pruebas de significación se han convertido en la forma dominante y casi exclusiva de análisis estadístico. Como consecuencia, las limitaciones de las pruebas han sido exhaustivamente estudiadas. Los libros se han llenado con la crítica recopilada de las pruebas de significancia.