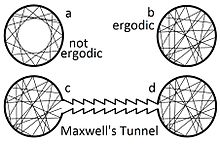
Hipótesis ergódica
En física y termodinámica, la hipótesis ergódica dice que, durante largos períodos de tiempo, el tiempo que pasa un sistema en alguna región del espacio de fase de microestados con la misma energía es proporcional a la volumen de esta región, es decir, que todos los microestados accesibles son equiprobables durante un largo período de tiempo.
El teorema de Liouville establece que, para un sistema hamiltoniano, la densidad local de los microestados que siguen la trayectoria de una partícula a través del espacio de fase es constante, tal como la ve un observador que se mueve con el conjunto (es decir, la derivada convectiva del tiempo es cero). Por lo tanto, si los microestados están inicialmente distribuidos uniformemente en el espacio de fases, permanecerán así en todo momento. Pero el teorema de Liouville no implica que la hipótesis ergódica se cumple para todos los sistemas hamiltonianos.
La hipótesis ergódica a menudo se asume en el análisis estadístico de la física computacional. El analista supondría que el promedio de un parámetro de proceso a lo largo del tiempo y el promedio del conjunto estadístico son iguales. Esta suposición, que es tan bueno simular un sistema durante un largo tiempo como hacer muchas realizaciones independientes del mismo sistema, no siempre es correcta. (Véase, por ejemplo, el experimento Fermi-Pasta-Ulam-Tsingou de 1953).
La asunción de la hipótesis ergódica permite probar que ciertos tipos de máquinas de movimiento perpetuo del segundo tipo son imposibles.
Se dice que los sistemas que son ergódicos tienen la propiedad de ergodicidad; una amplia gama de sistemas en geometría, física y teoría de probabilidad estocástica son ergódicas. Los sistemas ergódicos se estudian en la teoría ergódica.
Fenomenología
En los sistemas macroscópicos, las escalas de tiempo en las que un sistema puede realmente explorar la totalidad de su propio espacio de fase pueden ser lo suficientemente grandes como para que el estado de equilibrio termodinámico muestre alguna forma de ruptura de la ergodicidad. Un ejemplo común es el de la magnetización espontánea en sistemas ferromagnéticos, donde por debajo de la temperatura de Curie el sistema adopta preferentemente una magnetización distinta de cero, aunque la hipótesis ergódica implicaría que no debería existir magnetización neta en virtud de que el sistema explora todos los estados cuyo tiempo- la magnetización promediada debe ser cero. El hecho de que los sistemas macroscópicos a menudo violen la forma literal de la hipótesis ergódica es un ejemplo de ruptura de simetría espontánea.
Sin embargo, los sistemas desordenados complejos, como un vidrio giratorio, muestran una forma aún más complicada de ruptura de la ergodicidad en la que las propiedades del estado de equilibrio termodinámico visto en la práctica son mucho más difíciles de predecir únicamente mediante argumentos de simetría. También los vidrios convencionales (por ejemplo, vidrios para ventanas) violan la ergodicidad de manera complicada. En la práctica, esto significa que en escalas de tiempo suficientemente cortas (por ejemplo, de partes de segundos, minutos o unas pocas horas), los sistemas pueden comportarse como sólidos, es decir, con un módulo de corte positivo, pero en tiempos extremadamente largos. escalas, por ej. durante milenios o eones, como líquidos, o con dos o más escalas de tiempo y mesetas en el medio.
Hipótesis ergódica en finanzas
Los modelos utilizados en finanzas e inversión asumen la ergodicidad, explícita o implícitamente. La hipótesis ergódica prevalece en la teoría de cartera moderna, los modelos de flujo de efectivo descontado (DCF) y los modelos de indicadores agregados que infunden la macroeconomía, entre otros.
Las situaciones modeladas por estas teorías pueden ser útiles. Pero a menudo solo son útiles durante gran parte, pero no todo, de un período de tiempo particular bajo estudio. Por lo tanto, pueden pasar por alto algunas de las mayores desviaciones del modelo estándar, como las crisis financieras, las crisis de deuda y el riesgo sistémico en el sistema bancario que ocurren con poca frecuencia.
Nassim Nicholas Taleb ha argumentado que una parte muy importante de la realidad empírica en finanzas e inversiones no es ergódica. Una distribución estadística uniforme de probabilidades, en la que el sistema vuelve a todos los estados posibles un número infinito de veces, simplemente no es el caso que observamos en situaciones en las que "estados absorbentes" se alcanzan, un estado donde se ve ruina. La muerte de un individuo, o la pérdida total de todo, o la devolución o desmembramiento de un estado nación y el régimen legal que lo acompañó, son todos estados absorbentes. Por lo tanto, en finanzas, la dependencia de la ruta es importante. Un camino en el que un individuo, una empresa o un país llega a un "stop", una barrera absorbente, "cualquier cosa que impida que las personas con el pellejo en el juego salgan de él, y a los que el sistema tenderá invariablemente. Llamemos a estas situaciones ruina, ya que el ente no puede salir de la condición. El problema central es que si existe la posibilidad de ruina, los análisis de costo-beneficio ya no son posibles. Será no ergódico. Todos los modelos tradicionales basados en estadísticas probabilísticas estándar fallan en estas situaciones extremas.
Hipótesis ergódica en ciencias sociales
En las ciencias sociales, la hipótesis ergódica corresponde a la suposición de que los individuos son representativos de los grupos y viceversa, que los promedios de los grupos pueden caracterizar adecuadamente lo que se puede ver en un individuo. Parece que este no es el caso: los datos a nivel de grupo a menudo dan una mala indicación de la variación del nivel individual, ya que las desviaciones estándar (SD) individuales tienden a ser casi ocho veces mayores que las SD a nivel de grupo de las mismas personas. Posteriormente, un tercio de las observaciones individuales quedan fuera del intervalo de confianza del 99,9 % de los datos a nivel de grupo.
Contenido relacionado
Micron (desambiguación)
Dosimetría
Rodolfo koenig