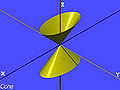
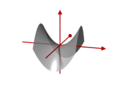
Hipérbola

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Curva del plano: sección cónica

Una hiperbola es una curva abierta con dos ramas, la intersección de un plano con ambas mitades de un cono doble. El plano no tiene que ser paralelo al eje del cono; la hiperbola será simétrica en cualquier caso.

Hyperbola (red): características

En matemáticas, una hipérbola (pl. hyperbolas o hyperbolae; adj. hipérbola) es un tipo de curva suave situada en un plano, definida por sus propiedades geométricas o por ecuaciones para las que es el conjunto solución. Una hipérbola tiene dos piezas, llamadas componentes conectados o ramas, que son imágenes especulares entre sí y se asemejan a dos arcos infinitos. La hipérbola es una de las tres clases de sección cónica, formada por la intersección de un plano y un doble cono. (Las otras secciones cónicas son la parábola y la elipse. Un círculo es un caso especial de una elipse). Si el plano interseca ambas mitades del cono doble pero no pasa por el vértice de los conos, entonces la cónica es una hipérbola..

Las hipérbolas surgen de muchas maneras:

como curva que representa la función recíproca ${displaystyle y(x)=1/x}$ en el plano cartesiano,
como el camino seguido por la sombra de la punta de un sundial,
como la forma de una órbita abierta (a diferencia de una órbita elíptica cerrada), como la órbita de una nave espacial durante una gravedad asistida oscilación por un planeta o, más generalmente, cualquier nave espacial (o objeto celestial) que supere la velocidad de escape del planeta más cercano u otro cuerpo gravitatorio,
como la trayectoria dispersa de una partícula subatómica (actuada por repulsivo en lugar de fuerzas atractivas, pero el principio es el mismo),
en la navegación por radio, cuando se puede determinar la diferencia entre distancias a dos puntos, pero no las distancias mismas,

y así sucesivamente.

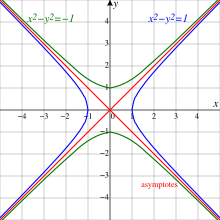
Cada rama de la hiperbola tiene dos brazos que se vuelven más rectos (curvatura más baja) más lejos del centro de la hiperbola. Los brazos diagonalmente opuestos, uno de cada rama, tienden en el límite a una línea común, llamada el asintoto de esos dos brazos. Así que hay dos asintotos, cuya intersección está en el centro de la simetría de la hiperbola, que se puede considerar como el punto de espejo sobre el cual cada rama refleja para formar la otra rama. En el caso de la curva ${displaystyle y(x)=1/x}$ los asintotos son los dos ejes de coordenadas.

Las hipérbolas comparten muchas de las elipses' propiedades analíticas tales como excentricidad, foco y directriz. Por lo general, la correspondencia se puede hacer con nada más que un cambio de signo en algún término. Muchos otros objetos matemáticos tienen su origen en la hipérbola, como los paraboloides hiperbólicos (superficies de silla de montar), los hiperboloides ("papeleras"), la geometría hiperbólica (la célebre geometría no euclidiana de Lobachevsky), las funciones hiperbólicas (sinh, cosh, tanh, etc.) y espacios girovectoriales (una geometría propuesta para su uso tanto en la relatividad como en la mecánica cuántica que no es euclidiana).

Etimología e historia

La palabra "hipérbola" deriva del griego ὑπερβολή, que significa "derribado" o "excesivo", de donde también deriva el término inglés hipérbole. Las hipérbolas fueron descubiertas por Menaechmus en sus investigaciones sobre el problema de doblar el cubo, pero luego se las llamó secciones de conos obtusos. Se cree que el término hipérbola fue acuñado por Apolonio de Perga (c. 262–c. 190 a. C.) en su obra definitiva sobre las secciones cónicas, las Cónicas. Los nombres de las otras dos secciones cónicas generales, la elipse y la parábola, derivan de las palabras griegas correspondientes para "deficiente" y "aplicado"; los tres nombres están tomados de la terminología pitagórica anterior que se refería a una comparación del lado de los rectángulos de área fija con un segmento de línea dado. El rectángulo se podría "aplicar" al segmento (es decir, tienen la misma longitud), ser más cortos que el segmento o exceder el segmento.

Definiciones

Como lugar geométrico de los puntos

Hyperbola: definición por las distancias de puntos a dos puntos fijos (foci)

Hyperbola: definición con directrix circular

Una hipérbola se puede definir geométricamente como un conjunto de puntos (lugar geométrico de los puntos) en el plano euclidiano:

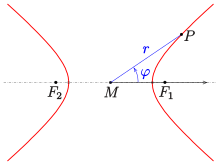
A hiperbola es un conjunto de puntos, tal que para cualquier punto

P

del conjunto, la diferencia absoluta de las distancias

{displaystyle |PF_{1}|,,|PF_{2}|}

a dos puntos fijos

F_{1},F_{2}

(Foci) es constante, generalmente denotado por

0}" xmlns="http://www.w3.org/1998/Math/MathML">2a,a■0{displaystyle 2a,,a}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/953d05ee106d48e80e648175ba027c4a4431d9c9" style="vertical-align: -0.671ex; width:9.304ex; height:2.509ex;"/>

{displaystyle H={P:left|left|PF_{2}right|-left|PF_{1}right|right|=2a}.}

El punto medio $M$ del segmento de línea que une el foci se llama centro de la hiperbola. La línea a través de la foci se llama eje principal. Contiene el vertices ${displaystyle V_{1},V_{2}}$ , que tienen distancia $a$ al centro. La distancia $c$ del foci al centro se llama el distancia focal o excentricidad lineal. El cociente ${displaystyle {tfrac {c}{a}}}$ es excentricidad $e$ .

La ecuación ${displaystyle ||PF_{2}|-|PF_{1}||=2a}$ se puede ver de una manera diferente (ver diagrama):
Si $c_{2}$ es el círculo con punto medio $F_{2}$ y radio $2a$ , entonces la distancia de un punto $P$ de la rama derecha al círculo $c_{2}$ iguala la distancia al foco $F_{1}$ :

{displaystyle |PF_{1}|=|Pc_{2}|.}

c_{2}

circular directrix

F_{2}

F_{1}

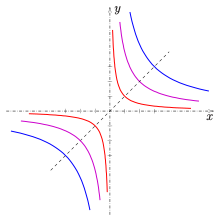
Hipérbola con ecuación y = A/x

Rotación del sistema de coordenadas para describir una hiperbola rectangular como gráfico de una función

Tres hiperbolas rectangulares

{displaystyle y=A/x}

con los ejes de coordenadas como
rojo: A = 1; magenta: A = 4; azul: A = 9

Si xy- sistema coordinado se gira sobre el origen por el ángulo ${displaystyle +45^{circ }}$ y nuevas coordenadas ${displaystyle xieta }$ son asignados, entonces ${displaystyle x={tfrac {xi +eta }{sqrt {2}}},;y={tfrac {-xi +eta }{sqrt {2}}}}$ .
La hiperbola rectangular ${displaystyle {tfrac {x^{2}-y^{2}}{a^{2}}}=1}$ (cuyos semi-axes son iguales) tiene la nueva ecuación ${displaystyle {tfrac {2xi eta }{a^{2}}}=1}$ . Solving for $eta$ rendimientos ${displaystyle eta ={tfrac {a^{2}/2}{xi }}.}$

Así, en un xy- sistema coordinado el gráfico de una función $0;,}" xmlns="http://www.w3.org/1998/Math/MathML">f:x↦ ↦ Ax,A■0,{displaystyle f:xmapsto {fnMicroc {A}{x},;A título0;,}0;,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/979904574a9809ad9220e2dbec9924553c0ecee3" style="vertical-align: -1.005ex; width:19.203ex; height:3.509ex;"/>$ con ecuación

0;,}" xmlns="http://www.w3.org/1998/Math/MathML">Sí.=Ax,A■0,{displaystyle y={frac ¿Qué?0;,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2e923b3902eb9deb0e8c3af450805e93bb9adc48" style="vertical-align: -1.838ex; width:15.808ex; height:5.343ex;"/>

es un hiperbola rectangular enteramente en los cuadrantes primero y tercero con

los ejes de coordenadas como asymptotes,
la línea $y=x$ como eje principal
el centro $(0,0)$ y el semi-eje ${displaystyle a=b={sqrt {2A}};,}$
el vertices ${displaystyle left({sqrt {A}},{sqrt {A}}right),left(-{sqrt {A}},-{sqrt {A}}right);,}$
el semi-latus recto y radio de curvatura en los vértices ${displaystyle p=a={sqrt {2A}};,}$
el excentricidad lineal ${displaystyle c=2{sqrt {A}}}$ y la excentricidad ${displaystyle e={sqrt {2}};,}$
el tangente ${displaystyle y=-{tfrac {A}{x_{0}^{2}}}x+2{tfrac {A}{x_{0}}}}$ punto ${displaystyle (x_{0},A/x_{0});.}$

Una rotación de la hiperbola original por ${displaystyle -45^{circ }}$ resultados en una hiperbola rectangular enteramente en los cuadrantes segundo y cuarto, con los mismos asintotos, centro, semi-latus recto, radio de curvatura en los vértices, excentricidad lineal, y excentricidad en el caso del caso ${displaystyle +45^{circ }}$ rotación, con ecuación

0;,}" xmlns="http://www.w3.org/1998/Math/MathML">Sí.=− − Ax,A■0,{displaystyle y={frac {-A}{x};,A título0;,}0;,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c9bf0b3045f7489e47d1d236fe9e5be26b6d9cd0" style="vertical-align: -1.838ex; width:17.616ex; height:5.343ex;"/>

el semi-axes ${displaystyle a=b={sqrt {2A}};,}$
la línea ${displaystyle y=-x}$ como eje principal,
el vertices ${displaystyle left(-{sqrt {A}},{sqrt {A}}right),left({sqrt {A}},-{sqrt {A}}right);.}$

Cambio de la hiperbola con ecuación ${displaystyle y={frac {A}{x}}, Aneq 0}$ así que el nuevo centro es ${displaystyle (c_{0},d_{0})}$ , produce la nueva ecuación

{displaystyle y={frac {A}{x-c_{0}}}+d_{0};,}

y los nuevos asintotos son ${displaystyle x=c_{0}}$ y ${displaystyle y=d_{0}}$ .
Los parámetros de la forma ${displaystyle a,b,p,c,e}$ permanecer sin cambios.

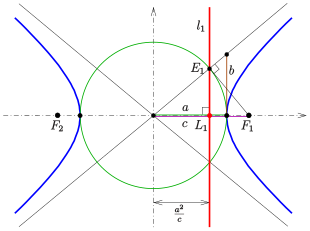
Por la propiedad de la directriz

Hyperbola: propiedad directrix

Hyperbola: definición con propiedad directrix

Las dos líneas a distancia ${textstyle d={frac {a^{2}}{c}}}$ desde el centro y paralelo al eje menor se llaman Directrices de la hiperbola (ver diagrama).

Para un punto arbitrario $P$ de la hiperbola el cociente de la distancia a un enfoque y al correspondiente directrix (ver diagrama) es igual a la excentricidad:

{displaystyle {frac {|PF_{1}|}{|Pl_{1}|}}={frac {|PF_{2}|}{|Pl_{2}|}}=e={frac {c}{a}}.}

La prueba para el par ${displaystyle F_{1},l_{1}}$ del hecho de que ${displaystyle |PF_{1}|^{2}=(x-c)^{2}+y^{2}, |Pl_{1}|^{2}=left(x-{tfrac {a^{2}}{c}}right)^{2}}$ y ${displaystyle y^{2}={tfrac {b^{2}}{a^{2}}}x^{2}-b^{2}}$ satisfacer la ecuación

{displaystyle |PF_{1}|^{2}-{frac {c^{2}}{a^{2}}}|Pl_{1}|^{2}=0.}

El segundo caso se prueba de forma análoga.

Ápice de conics con un vértice común y recto semi-lato común

La proposición inversa también es verdadera y se puede usar para definir una hipérbola (de manera similar a la definición de una parábola):

Para cualquier punto $F$ (enfoque), cualquier línea $l$ (directrix) not through $F$ y cualquier número real $e$ con $1}" xmlns="http://www.w3.org/1998/Math/MathML">e■1{displaystyle e confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9605ca17e3915b659685c0326fbbcbfb522f11b3" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>$ el conjunto de puntos (luz de puntos), para los cuales el cociente de las distancias al punto y a la línea es $e$

{displaystyle H=left{P,{Biggr |},{frac {|PF|}{|Pl|}}=eright}}

es una hiperbola.

(La elección $e=1$ cede una parabola y si $<math alttext="{displaystyle ee.1{displaystyle e won1} <img alt="{displaystyle e$ un elipse.)

Prueba

Vamos $0}" xmlns="http://www.w3.org/1998/Math/MathML">F=()f,0),e■0{displaystyle F=(f,0), e título0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4f988ef1675c91f286332c94191bfd6b53674ba5" style="vertical-align: -0.838ex; width:17.083ex; height:2.843ex;"/>$ y asumir $(0,0)$ es un punto en la curva. El directo $l$ tiene ecuación ${displaystyle x=-{tfrac {f}{e}}}$ . Con $P=(x,y)$ , la relación ${displaystyle |PF|^{2}=e^{2}|Pl|^{2}}$ produce las ecuaciones

{displaystyle (x-f)^{2}+y^{2}=e^{2}left(x+{tfrac {f}{e}}right)^{2}=(ex+f)^{2}}

{displaystyle x^{2}(e^{2}-1)+2xf(1+e)-y^{2}=0.}

La sustitución ${displaystyle p=f(1+e)}$ rendimientos

{displaystyle x^{2}(e^{2}-1)+2px-y^{2}=0.}

Esta es la ecuación de un elipse () $<math alttext="{displaystyle ee.1{displaystyle e won1} <img alt="e$ ) o un parabola () $e=1$ ) o un hiperbola () $1}" xmlns="http://www.w3.org/1998/Math/MathML">e■1{displaystyle e confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9605ca17e3915b659685c0326fbbcbfb522f11b3" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>$ ). Todos estos conics no degenerados tienen, en común, el origen como un vértice (ver diagrama).

Si $1}" xmlns="http://www.w3.org/1998/Math/MathML">e■1{displaystyle e confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9605ca17e3915b659685c0326fbbcbfb522f11b3" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>$ , introducir nuevos parámetros $a,b$ así ${displaystyle e^{2}-1={tfrac {b^{2}}{a^{2}}},{text{ and }} p={tfrac {b^{2}}{a}}}$ , y entonces la ecuación anterior se convierte

{displaystyle {tfrac {(x+a)^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1}

que es la ecuación de una hiperbola con centro ${displaystyle (-a,0)}$ , el x-eje como eje principal y el eje semi mayor/minor $a,b$ .

Hyperbola: construcción de un directrix

Construcción de un directrix

Debido a ${displaystyle ccdot {tfrac {a^{2}}{c}}=a^{2}}$ punto $L_{1}$ de directrix $l_{1}$ (ver diagrama) y enfoque $F_{1}$ son inversos con respecto a la inversión del círculo en círculo ${displaystyle x^{2}+y^{2}=a^{2}}$ (en el diagrama verde). Por aquí $E_{1}$ se puede construir utilizando el teorema de Thales (no se muestra en el diagrama). El directrix $l_{1}$ es el perpendicular a la línea ${displaystyle {overline {F_{1}F_{2}}}}$ a través del punto $E_{1}$ .
Construcción alternativa $E_{1}$ : Cálculo muestra, ese punto $E_{1}$ es la intersección del asintoto con su perpendicular a través $F_{1}$ (ver diagrama).

Como sección plana de un cono

Hyperbola (red): dos vistas de un cono y dos esferas de Dandelin d₁, d₂

La intersección de un cono doble recto por un plano no a través del vértice con pendiente mayor que la pendiente de las líneas en el cono es una hiperbola (ver diagrama: curva roja). Para probar la propiedad definitoria de una hiperbola (ver arriba) se utiliza dos esferas de Dandelin $d_{1},d_{2}$ , que son esferas que tocan el cono a lo largo de círculos $c_{1}$ ${displaystyle c_{2}}$ y el plano de intersección (hiperbola) en puntos $F_{1}$ y $F_{2}$ . Resulta que: $F_{1},F_{2}$ son Foci de la hiperbola.

Vamos $P$ ser un punto arbitrario de la curva de intersección.
El génerotrix del cono que contiene $P$ intersects circle $c_{1}$ punto $A$ y círculo $c_{2}$ en un momento $B$ .
Los segmentos de línea ${displaystyle {overline {PF_{1}}}}$ y ${displaystyle {overline {PA}}}$ son tangenciales a la esfera $d_{1}$ y, por lo tanto, son de igual longitud.
Los segmentos de línea ${displaystyle {overline {PF_{2}}}}$ y ${displaystyle {overline {PB}}}$ son tangenciales a la esfera $d_{2}$ y, por lo tanto, son de igual longitud.
El resultado es: ${displaystyle |PF_{1}|-|PF_{2}|=|PA|-|PB|=|AB|}$ es independiente del punto hiperbola $P$ , porque no importa dónde punto $P$ es, $A,B$ tienen que estar en círculos $c_{1}$ ${displaystyle c_{2}}$ , y segmento de línea $AB$ tiene que cruzar el ápice. Por lo tanto, como punto $P$ se mueve a lo largo de la curva roja (hiperbola), segmento de línea ${overline {AB}}$ simplemente gira alrededor del ápice sin cambiar su longitud.

Construcción con pasadores y cuerdas

Hyperbola: Construcción de pins y cadenas

La definición de una hipérbola por sus focos y sus directrices circulares (ver arriba) se puede usar para dibujar un arco con la ayuda de alfileres, una cuerda y una regla:

Elija el Foci $F_{1},F_{2}$ , los vértices ${displaystyle V_{1},V_{2}}$ y uno de los circular directrices por ejemplo $c_{2}$ (circo con radio $2a$ )
A ruler se fija en el punto $F_{2}$ libre para girar alrededor $F_{2}$ . Punto $B$ está marcado a distancia $2a$ .
A cuerda con longitud ${displaystyle |AB|}$ está preparado.
Un extremo de la cuerda se fija en el punto $A$ en el gobernante, el otro extremo está marcado a punto $F_{1}$ .
Toma. pluma y mantener la cuerda ajustada al borde del gobernante.
Rotación la regla alrededor $F_{2}$ incita al bolígrafo a dibujar un arco de la rama derecha de la hiperbola, debido a ${displaystyle |PF_{1}|=|PB|}$ (ver la definición de hiperbola por circular directrices).

Generación de Steiner de una hipérbola

Hyperbola: Steiner generation

Hyperbola Sí. 1/x: Steiner generation

El siguiente método para construir puntos únicos de una hipérbola se basa en la generación de Steiner de una sección cónica no degenerada:

Dado dos lápices

B(U),B(V)

líneas en dos puntos

U,V

(todas las líneas que contienen

U

V

, respectivamente) y una asignación proyectiva pero no perspectiva

pi

B(U)

sobre

B(V)

, entonces los puntos de intersección de las líneas correspondientes forman una sección conic proyectiva no degenerada.

Para la generación de puntos de la hiperbola ${displaystyle {tfrac {x^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1}$ uno utiliza los lápices en los vértices ${displaystyle V_{1},V_{2}}$ . Vamos ${displaystyle P=(x_{0},y_{0})}$ ser un punto de la hiperbola y ${displaystyle A=(a,y_{0}),B=(x_{0},0)}$ . El segmento de línea ${displaystyle {overline {BP}}}$ se divide en segmentos de igual espacio y esta división se proyecta paralelamente con la diagonal $AB$ como dirección en el segmento de línea ${displaystyle {overline {AP}}}$ (ver diagrama). La proyección paralela es parte de la cartografía proyectiva entre los lápices en $V_{1}$ y $V_{2}$ necesario. Los puntos de intersección de las dos líneas conexas ${displaystyle S_{1}A_{i}}$ y ${displaystyle S_{2}B_{i}}$ son puntos de la hiperbola única definida.

Observación: La subdivisión podría ampliarse más allá de los puntos $A$ y $B$ para obtener más puntos, pero la determinación de los puntos de intersección sería más inexacta. Una mejor idea es ampliar los puntos ya construidos por simetría (ver animación).

Observación:

La generación Steiner también existe para elipses y parabolas.
La generación Steiner a veces se llama método para paralelograma porque uno puede utilizar otros puntos en lugar de los vértices, que comienza con un paralelograma en lugar de un rectángulo.

Ángulos inscritos para hipérbolas y = a/(x − b) + c y la forma de 3 puntos

Hyperbola: teorema de ángulo inscrito

Una hiperbola con ecuación ${displaystyle y={tfrac {a}{x-b}}+c, aneq 0}$ está determinado por tres puntos ${displaystyle (x_{1},y_{1}),;(x_{2},y_{2}),;(x_{3},y_{3})}$ con diferente x- y Sí.- coordinación. Una manera sencilla de determinar los parámetros de forma $a,b,c$ usos teorema de ángulo inscrito para hiperbolas:

Para medir un ángulo entre dos líneas con ecuaciones

{displaystyle y=m_{1}x+d_{1}, y=m_{2}x+d_{2}m_{1},m_{2}neq 0}

en este contexto se utiliza el coeficiente

{displaystyle {frac {m_{1}}{m_{2}}}.}

Análogo al teorema del ángulo inscrito para círculos, se obtiene el

Teorema del ángulo inscrito para hipérbolas:

Para cuatro puntos

{displaystyle P_{i}=(x_{i},y_{i}), i=1,2,3,4, x_{i}neq x_{k},y_{i}neq y_{k},ineq k}

(ver diagrama) la siguiente declaración es verdadera:

Los cuatro puntos están en una hiperbola con ecuación

{displaystyle y={tfrac {a}{x-b}}+c}

si y sólo si los ángulos

P_{3}

P_{4}

son iguales en el sentido de la medición anterior. Eso significa si

{displaystyle {frac {(y_{4}-y_{1})}{(x_{4}-x_{1})}}{frac {(x_{4}-x_{2})}{(y_{4}-y_{2})}}={frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}{frac {(x_{3}-x_{2})}{(y_{3}-y_{2})}}}

(Proof: cálculo directo. Si los puntos están en una hiperbola, uno puede asumir que la ecuación de la hiperbola es ${displaystyle y=a/x}$ .)

Una consecuencia del teorema del ángulo inscrito para las hipérbolas es la

Forma de 3 puntos de la ecuación de una hipérbola:

La ecuación de la hiperbola determinada por 3 puntos

{displaystyle P_{i}=(x_{i},y_{i}), i=1,2,3, x_{i}neq x_{k},y_{i}neq y_{k},ineq k}

es la solución de la ecuación

{displaystyle {frac {({color {red}y}-y_{1})}{({color {green}x}-x_{1})}}{frac {({color {green}x}-x_{2})}{({color {red}y}-y_{2})}}={frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}{frac {(x_{3}-x_{2})}{(y_{3}-y_{2})}}}

para

{displaystyle {color {red}y}}

Como una imagen afín de la unidad hipérbola x² − y² = 1

Hyperbola como imagen afinada de la unidad hiperbola

Otra definición de una hipérbola utiliza transformaciones afines:

Cualquier hiperbola es la imagen afine de la unidad hiperbola con ecuación

x^2-y^2=1

Representación paramétrica

Una transformación afinada del plano Euclideano tiene la forma ${displaystyle {vec {x}}to {vec {f}}_{0}+A{vec {x}}}$ , donde $A$ es una matriz regular (su determinante no es 0) y ${displaystyle {vec {f}}_{0}}$ es un vector arbitrario. Si ${displaystyle {vec {f}}_{1},{vec {f}}_{2}}$ son los vectores de columna de la matriz $A$ , la unidad hiperbola ${displaystyle (pm cosh(t),sinh(t)),tin mathbb {R}}$ se mapea en la hiperbola

{displaystyle {vec {x}}={vec {p}}(t)={vec {f}}_{0}pm {vec {f}}_{1}cosh t+{vec {f}}_{2}sinh t.}

${displaystyle {vec {f}}_{0}}$ es el centro, ${displaystyle {vec {f}}_{0}+{vec {f}}_{1}}$ un punto de la hiperbola y ${displaystyle {vec {f}}_{2}}$ un vector tangente en este punto.

vertices

En general los vectores ${displaystyle {vec {f}}_{1},{vec {f}}_{2}}$ no son perpendiculares. Eso significa, en general ${displaystyle {vec {f}}_{0}pm {vec {f}}_{1}}$ son no los vértices de la hiperbola. Pero... ${displaystyle {vec {f}}_{1}pm {vec {f}}_{2}}$ apuntar a las direcciones de los asintotos. El vector tangente en punto ${displaystyle {vec {p}}(t)}$ es

{displaystyle {vec {p}}'(t)={vec {f}}_{1}sinh t+{vec {f}}_{2}cosh t.}

Porque en un vértice el tangente es perpendicular al eje mayor de la hiperbola se obtiene el parámetro $t_{0}$ de un vértice de la ecuación

{displaystyle {vec {p}}'(t)cdot left({vec {p}}(t)-{vec {f}}_{0}right)=left({vec {f}}_{1}sinh t+{vec {f}}_{2}cosh tright)cdot left({vec {f}}_{1}cosh t+{vec {f}}_{2}sinh tright)=0}

y por lo tanto de

{displaystyle coth(2t_{0})=-{tfrac {{vec {f}}_{1}^{,2}+{vec {f}}_{2}^{,2}}{2{vec {f}}_{1}cdot {vec {f}}_{2}}}}

que produce

{displaystyle t_{0}={tfrac {1}{4}}ln {tfrac {left({vec {f}}_{1}-{vec {f}}_{2}right)^{2}}{left({vec {f}}_{1}+{vec {f}}_{2}right)^{2}}}.}

(La fórmula) ${displaystyle cosh ^{2}x+sinh ^{2}x=cosh 2x, 2sinh xcosh x=sinh 2x, operatorname {arcoth} x={tfrac {1}{2}}ln {tfrac {x+1}{x-1}}}$ fueron utilizados.)

Los dos vertices de la hiperbola son ${displaystyle {vec {f}}_{0}pm left({vec {f}}_{1}cosh t_{0}+{vec {f}}_{2}sinh t_{0}right).}$

representación implícita

Resolver la representación paramétrica ${displaystyle ;cosh t,sinh t;}$ por la regla de Cramer y usando ${displaystyle ;cosh ^{2}t-sinh ^{2}t-1=0;}$ , uno consigue la representación implícita

{displaystyle det({vec {x}}!-!{vec {f}}!_{0},{vec {f}}!_{2})^{2}-det({vec {f}}!_{1},{vec {x}}!-!{vec {f}}!_{0})^{2}-det({vec {f}}!_{1},{vec {f}}!_{2})^{2}=0}

hiperbola en el espacio

La definición de hiperbola en esta sección da una representación paramétrica de una hiperbola arbitraria, incluso en el espacio, si se permite ${displaystyle {vec {f}}!_{0},{vec {f}}!_{1},{vec {f}}!_{2}}$ ser vectores en el espacio.

Como imagen afín de la hipérbola y = 1/x

Hyperbola como imagen afinada de Sí. 1/x

Porque la unidad hiperbola $x^2-y^2=1$ es afinalmente equivalente a la hiperbola $y=1/x$ , una hiperbola arbitraria se puede considerar como la imagen afine (ver sección anterior) de la hiperbola ${displaystyle y=1/x:}$

{displaystyle {vec {x}}={vec {p}}(t)={vec {f}}_{0}+{vec {f}}_{1}t+{vec {f}}_{2}{tfrac {1}{t}},quad tneq 0.}

${displaystyle M:{vec {f}}_{0}}$ es el centro de la hiperbola, los vectores ${displaystyle {vec {f}}_{1},{vec {f}}_{2}}$ tienen las direcciones de los asintotos y ${displaystyle {vec {f}}_{1}+{vec {f}}_{2}}$ es un punto de la hiperbola. El vector tangente es

{displaystyle {vec {p}}'(t)={vec {f}}_{1}-{vec {f}}_{2}{tfrac {1}{t^{2}}}.}

En un vértice la tangente es perpendicular al eje mayor. Por eso

{displaystyle {vec {p}}'(t)cdot left({vec {p}}(t)-{vec {f}}_{0}right)=left({vec {f}}_{1}-{vec {f}}_{2}{tfrac {1}{t^{2}}}right)cdot left({vec {f}}_{1}t+{vec {f}}_{2}{tfrac {1}{t}}right)={vec {f}}_{1}^{2}t-{vec {f}}_{2}^{2}{tfrac {1}{t^{3}}}=0}

y el parámetro de un vértice es

{displaystyle t_{0}=pm {sqrt[{4}]{tfrac {{vec {f}}_{2}^{2}}{{vec {f}}_{1}^{2}}}}.}

${displaystyle |{vec {f}}_{1}|=|{vec {f}}_{2}|}$ equivale a ${displaystyle t_{0}=pm 1}$ y ${displaystyle {vec {f}}_{0}pm ({vec {f}}_{1}+{vec {f}}_{2})}$ son los vértices de la hiperbola.

Las siguientes propiedades de una hipérbola se prueban fácilmente usando la representación de una hipérbola presentada en esta sección.

Construcción tangente

Construcción tangente: asintotos y P dado → tangente

El vector tangente se puede reescribir por factorización:

{displaystyle {vec {p}}'(t)={tfrac {1}{t}}left({vec {f}}_{1}t-{vec {f}}_{2}{tfrac {1}{t}}right).}

Esto significa que

la diagonal

AB

del paralelograma

{displaystyle M: {vec {f}}_{0}, A={vec {f}}_{0}+{vec {f}}_{1}t, B: {vec {f}}_{0}+{vec {f}}_{2}{tfrac {1}{t}}, P: {vec {f}}_{0}+{vec {f}}_{1}t+{vec {f}}_{2}{tfrac {1}{t}}}

es paralelo al tangente en el punto hiperbola

P

(ver diagrama).

Esta propiedad proporciona una forma de construir la tangente en un punto de la hipérbola.

Esta propiedad de una hipérbola es una versión afín de la degeneración de 3 puntos del teorema de Pascal.

Área del paralelograma gris

El área del paralelograma gris ${displaystyle MAPB}$ en el diagrama anterior

{displaystyle {text{Area}}={Big |}det left(t{vec {f}}_{1},{tfrac {1}{t}}{vec {f}}_{2}right){Big |}={Big |}det left({vec {f}}_{1},{vec {f}}_{2}right){Big |}=cdots ={frac {a^{2}+b^{2}}{4}}}

y, por consiguiente, independiente del punto $P$ . La última ecuación sigue de un cálculo para el caso, donde $P$ es un vértice y la hiperbola en su forma canónica ${displaystyle {tfrac {x^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1.}$

Construcción de puntos

Construcción de puntos: asintotos y P₁ se dan → P₂

Para una hiperbola con representación paramétrica ${displaystyle {vec {x}}={vec {p}}(t)={vec {f}}_{1}t+{vec {f}}_{2}{tfrac {1}{t}}}$ (para simplicidad el centro es el origen) lo siguiente es cierto:

Por dos puntos

{displaystyle P_{1}: {vec {f}}_{1}t_{1}+{vec {f}}_{2}{tfrac {1}{t_{1}}}, P_{2}: {vec {f}}_{1}t_{2}+{vec {f}}_{2}{tfrac {1}{t_{2}}}}

los puntos

{displaystyle A: {vec {a}}={vec {f}}_{1}t_{1}+{vec {f}}_{2}{tfrac {1}{t_{2}}}, B: {vec {b}}={vec {f}}_{1}t_{2}+{vec {f}}_{2}{tfrac {1}{t_{1}}}}

son collinear con el centro de la hiperbola (ver diagrama).

La prueba simple es una consecuencia de la ecuación ${displaystyle {tfrac {1}{t_{1}}}{vec {a}}={tfrac {1}{t_{2}}}{vec {b}}}$ .

Esta propiedad brinda la posibilidad de construir puntos de una hipérbola si se dan las asíntotas y un punto.

Esta propiedad de una hipérbola es una versión afín de la degeneración de 4 puntos del teorema de Pascal.

Tangente-asintotas-triángulo

Hyperbola: tangente-asymptotes-triángulo

Para la simplicidad el centro de la hiperbola puede ser el origen y los vectores ${displaystyle {vec {f}}_{1},{vec {f}}_{2}}$ tienen igual longitud. Si la última suposición no se cumple se puede aplicar primero una transformación del parámetro (ver arriba) para hacer realidad la suposición. Por lo tanto ${displaystyle pm ({vec {f}}_{1}+{vec {f}}_{2})}$ son los vértices, ${displaystyle pm ({vec {f}}_{1}-{vec {f}}_{2})}$ el eje menor y uno consigue ${displaystyle |{vec {f}}_{1}+{vec {f}}_{2}|=a}$ y ${displaystyle |{vec {f}}_{1}-{vec {f}}_{2}|=b}$ .

Para los puntos de intersección del tangente en punto ${displaystyle {vec {p}}(t_{0})={vec {f}}_{1}t_{0}+{vec {f}}_{2}{tfrac {1}{t_{0}}}}$ con los asintotes uno consigue los puntos

{displaystyle C=2t_{0}{vec {f}}_{1}, D={tfrac {2}{t_{0}}}{vec {f}}_{2}.}

El zona del triángulo ${displaystyle M,C,D}$ puede ser calculado por un 2 × 2 determinante:

{displaystyle A={tfrac {1}{2}}{Big |}det left(2t_{0}{vec {f}}_{1},{tfrac {2}{t_{0}}}{vec {f}}_{2}right){Big |}=2{Big |}det left({vec {f}}_{1},{vec {f}}_{2}right){Big |}}

(ver reglas para los determinantes). ${displaystyle |det({vec {f}}_{1},{vec {f}}_{2})|}$ es el área del rombo generado por ${displaystyle {vec {f}}_{1},{vec {f}}_{2}}$ . El área de un rombo es igual a la mitad del producto de sus diagonales. Las diagonales son las semi-axas $a,b$ de la hiperbola. Por lo tanto:

El zona del triángulo

{displaystyle MCD}

es independiente del punto de la hiperbola:

{displaystyle A=ab.}

Reciprocidad de un círculo

La reciprocidad de un círculo B en un círculo C siempre produce una sección cónica como una hipérbola. El proceso de "reciprocidad en un círculo C" consiste en sustituir cada recta y punto de una figura geométrica por su correspondiente polo y polar, respectivamente. El polo de una línea es la inversión de su punto más cercano al círculo C, mientras que el polar de un punto es lo contrario, es decir, una línea cuyo punto más cercano a C es la inversión del punto.

La excentricidad de la sección cónica obtenida por vaivén es la relación de las distancias entre los dos círculos' centros al radio r del círculo de reciprocidad C. Si B y C representan los puntos en los centros de los círculos correspondientes, entonces

e = frac{overline{BC}}{r}.

Dado que la excentricidad de una hipérbola siempre es mayor que uno, el centro B debe estar fuera del círculo alternativo C.

Esta definición implica que la hipérbola es tanto el lugar geométrico de los polos de las rectas tangentes a la circunferencia B, como la envolvente de las rectas polares de los puntos sobre B. Por el contrario, la circunferencia B es la envolvente de las polares de los puntos de la hipérbola y el lugar geométrico de las polares de las tangentes a la hipérbola. Dos rectas tangentes a B no tienen polos (finitos) porque pasan por el centro C del círculo de reciprocidad C; las polares de los puntos tangentes correspondientes en B son las asíntotas de la hipérbola. Las dos ramas de la hipérbola corresponden a las dos partes del círculo B que están separadas por estos puntos tangentes.

Ecuación cuadrática

Una hipérbola también se puede definir como una ecuación de segundo grado en las coordenadas cartesianas (x, y) en el plano,

{displaystyle A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0,}

siempre que las constantes A_xx, A_xy, A_aa, B_x, B_y y C satisfacen la condición determinante

<math alttext="{displaystyle D:={begin{vmatrix}A_{xx}&A_{xy}\A_{xy}&A_{yy}end{vmatrix}}D:=SilencioAxxAxSí.AxSí.ASí.Sí.Silencio.0.{displaystyle D:={begin{vmatrix}A_{xx} {xy}A_{xy} limitA_{yy}end{vmatrix}}} {0},}}<img alt=" D:= begin{vmatrix} A_{xx} & A_{xy}\A_{xy} & A_{yy} end{vmatrix}

Este determinante se denomina convencionalmente el discriminante de la sección cónica.

Un caso especial de hipérbola, la hipérbola degenerada que consiste en dos líneas que se cruzan, ocurre cuando otro determinante es cero:

{displaystyle Delta:={begin{vmatrix}A_{xx}&A_{xy}&B_{x}\A_{xy}&A_{yy}&B_{y}\B_{x}&B_{y}&Cend{vmatrix}}=0.}

Este determinante Δ a veces se llama el discriminante de la sección cónica.

Dada la parametrización general anterior de la hipérbola en coordenadas cartesianas, la excentricidad se puede encontrar utilizando la fórmula en Sección cónica#Excentricidad en términos de coeficientes.

El centro (x_c, y_c) de la hipérbola se puede determinar a partir de las fórmulas

{displaystyle x_{c}=-{frac {1}{D}}{begin{vmatrix}B_{x}&A_{xy}\B_{y}&A_{yy}end{vmatrix}};}

{displaystyle y_{c}=-{frac {1}{D}}{begin{vmatrix}A_{xx}&B_{x}\A_{xy}&B_{y}end{vmatrix}}.}

En términos de nuevas coordenadas, ξ = x − x_c y η = y − y_c, la ecuación definitoria de la hipérbola se puede escribir

{displaystyle A_{xx}xi ^{2}+2A_{xy}xi eta +A_{yy}eta ^{2}+{frac {Delta }{D}}=0.}

Los ejes principales de la hipérbola forman un ángulo φ con el eje positivo x que viene dado por

{displaystyle tan 2varphi ={frac {2A_{xy}}{A_{xx}-A_{yy}}}.}

Al girar los ejes de coordenadas de manera que el eje x esté alineado con el eje transversal, la ecuación adquiere su forma canónica

{frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1.

Los semiejes mayor y menor a y b están definidos por las ecuaciones

{displaystyle a^{2}=-{frac {Delta }{lambda _{1}D}}=-{frac {Delta }{lambda _{1}^{2}lambda _{2}}},}

{displaystyle b^{2}=-{frac {Delta }{lambda _{2}D}}=-{frac {Delta }{lambda _{1}lambda _{2}^{2}}},}

donde λ₁ y λ₂ son las raíces de la ecuación cuadrática

{displaystyle lambda ^{2}-left(A_{xx}+A_{yy}right)lambda +D=0.}

A modo de comparación, la ecuación correspondiente para una hipérbola degenerada (que consta de dos líneas que se cruzan) es

{displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=0.}

Se define la recta tangente a un punto dado (x₀, y₀) en la hipérbola por la ecuación

{displaystyle Ex+Fy+G=0}

donde E, F y G están definidos por

{displaystyle E=A_{xx}x_{0}+A_{xy}y_{0}+B_{x},}

{displaystyle F=A_{xy}x_{0}+A_{yy}y_{0}+B_{y},}

{displaystyle G=B_{x}x_{0}+B_{y}y_{0}+C.}

La recta normal a la hipérbola en el mismo punto viene dada por la ecuación

{displaystyle F(x-x_{0})-E(y-y_{0})=0.}

La recta normal es perpendicular a la recta tangente, y ambas pasan por el mismo punto (x₀, y₀).

De la ecuación

<math alttext="{displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1,qquad 0x2a2− − Sí.2b2=1,0.b≤ ≤ a,{displaystyle {frac {x^{2}{a^{2}}-{frac} {y} {y}{b^{2}}=1,qquad 0,2 a<img alt="{displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1,qquad 0

el foco izquierdo ${displaystyle (-ae,0)}$ y el enfoque correcto ${displaystyle (ae,0),}$ Donde $e$ es la excentricidad. Denota las distancias desde un punto (x, y) a la izquierda y derecha foci as $r_1 ,!$ y ${displaystyle r_{2}.,!}$ Por un punto en la rama derecha,

{displaystyle r_{1}-r_{2}=2a,,!}

y para un punto en la rama izquierda,

{displaystyle r_{2}-r_{1}=2a.,!}

Esto se puede demostrar de la siguiente manera:

Si (x,y) es un punto en la hipérbola, la distancia al punto focal izquierdo es

{displaystyle r_{1}^{2}=(x+ae)^{2}+y^{2}=x^{2}+2xae+a^{2}e^{2}+left(x^{2}-a^{2}right)left(e^{2}-1right)=(ex+a)^{2}.}

Al punto focal derecho la distancia es

{displaystyle r_{2}^{2}=(x-ae)^{2}+y^{2}=x^{2}-2xae+a^{2}e^{2}+left(x^{2}-a^{2}right)left(e^{2}-1right)=(ex-a)^{2}.}

Six,Sí.) es un punto en la rama derecha de la hiperbola entonces $a,!}" xmlns="http://www.w3.org/1998/Math/MathML">ex■a{displaystyle ex confiadoa,fnMicrosoft Sans Serif} a,!" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a7be3714c2ac95e15f7dc27b9e20760a3179a3e4" style="vertical-align: -0.338ex; margin-right: -0.387ex; width:7.129ex; height:1.843ex;"/>$ y

{displaystyle r_{1}=ex+a,,!}

{displaystyle r_{2}=ex-a.,!}

Al restar estas ecuaciones se obtiene

{displaystyle r_{1}-r_{2}=2a.,!}

Six,y) es un punto en la rama izquierda de la hiperbola entonces $<math alttext="{displaystyle exex.- - a{displaystyle ex done-a,!} <img alt="e x$ y

{displaystyle r_{1}=-ex-a,,!}

{displaystyle r_{2}=-ex+a.,!}

Al restar estas ecuaciones se obtiene

{displaystyle r_{2}-r_{1}=2a.,!}

En coordenadas cartesianas

Ecuación

Si las coordenadas cartesianas se introducen de modo que el origen sea el centro de la hipérbola y el eje x sea el eje mayor, entonces la hipérbola se denomina apertura este-oeste y

el Foci son los puntos ${displaystyle F_{1}=(c,0), F_{2}=(-c,0)}$ ,

el vertices son ${displaystyle V_{1}=(a,0), V_{2}=(-a,0)}$ .

Para un punto arbitrario $(x,y)$ la distancia al foco $(c,0)$ es ${displaystyle {sqrt {(x-c)^{2}+y^{2}}}}$ y para el segundo enfoque ${displaystyle {sqrt {(x+c)^{2}+y^{2}}}}$ . Por lo tanto el punto $(x,y)$ está en la hiperbola si se cumple la siguiente condición

${displaystyle {sqrt {(x-c)^{2}+y^{2}}}-{sqrt {(x+c)^{2}+y^{2}}}=pm 2a.}$

Quitar las raíces cuadradas por los revestimientos adecuados y utilizar la relación ${displaystyle b^{2}=c^{2}-a^{2}}$ para obtener la ecuación de la hiperbola:

${displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1.}$

Esta ecuación se llama la forma canónica de una hipérbola, porque cualquier hipérbola, independientemente de su orientación relativa a los ejes cartesianos y de la ubicación de su centro, puede transformarse a esta forma mediante un cambio de variables, dando un hipérbola que es congruente con el original (ver más abajo).

Los ejes de la simetría o ejes principales son eje transversal (contiene el segmento de la longitud 2a con puntos finales en los vértices) y conjugar el eje (contiene el segmento de la longitud 2b perpendicular al eje transversal y con punto medio en el centro de la hiperbola). A diferencia de un elipse, una hiperbola tiene sólo dos vértices: ${displaystyle (a,0),;(-a,0)}$ . Los dos puntos ${displaystyle (0,b),;(0,-b)}$ sobre los ejes conjugados no en la hiperbola.

Se deduce de la ecuación que la hipérbola es simétrica con respecto a ambos ejes de coordenadas y, por lo tanto, simétrica con respecto al origen.

Excentricidad

Para una hipérbola en la forma canónica anterior, la excentricidad está dada por

${textstyle e={sqrt {1+{frac {b^{2}}{a^{2}}}}}.}$

Dos hipérbolas son geométricamente similares entre sí, lo que significa que tienen la misma forma, por lo que una puede transformarse en la otra mediante movimientos rígidos hacia la izquierda y hacia la derecha, rotación, toma de una imagen especular y escala (ampliación), si y solo si tienen la misma excentricidad.

Asíntotas

Hyperbola: semi-axes a,b, excentricidad lineal c, semi latus recto p

Hyperbola: 3 propiedades

Resolver la ecuación (arriba) de la hiperbola para $y$ rendimientos

${displaystyle y=pm {frac {b}{a}}{sqrt {x^{2}-a^{2}}}.}$

Se sigue de esto que la hipérbola se acerca a las dos líneas

${displaystyle y=pm {frac {b}{a}}x}$

para grandes valores $|x|$ . Estas dos líneas se intersectan en el centro (origin) y se llaman asymptotes de la hiperbola ${displaystyle {tfrac {x^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1.}$

Con la ayuda de la segunda figura se puede ver que

${displaystyle {color {blue}{(1)}}}$ El distancia perpendicular de un enfoque a asintoto es $b$ (el eje semi-minor).

De la forma normal Hesse ${displaystyle {tfrac {bxpm ay}{sqrt {a^{2}+b^{2}}}}=0}$ de los asintotos y la ecuación de la hiperbola se obtiene:

${displaystyle {color {magenta}{(2)}}}$ El producto de las distancias desde un punto en la hiperbola a ambos los asintotos es la constante ${displaystyle {tfrac {a^{2}b^{2}}{a^{2}+b^{2}}}}$ que también se puede escribir en términos de la excentricidad e como ${displaystyle left({tfrac {b}{e}}right)^{2}.}$

De la ecuación ${displaystyle y=pm {frac {b}{a}}{sqrt {x^{2}-a^{2}}}}$ de la hiperbola (arriba) se puede derivar:

${displaystyle {color {green}{(3)}}}$ El producto de las pendientes de líneas de un punto P a los dos vértices es la constante ${displaystyle b^{2}/a^{2}.}$

Además, de (2) arriba se puede demostrar que

${displaystyle {color {red}{(4)}}}$ El producto de las distancias de un punto en la hiperbola a los asintotos en líneas paralelas a los asintotos es la constante ${displaystyle {tfrac {a^{2}+b^{2}}{4}}.}$

Recto semilato

La longitud del acorde a través de uno de los foci, perpendicular al eje mayor de la hiperbola, se llama el el recto. Una mitad es la semi-latus recto $p$ . Un cálculo muestra

${displaystyle p={frac {b^{2}}{a}}.}$

El recto semi-latus $p$ también se puede considerar como radio de curvatura en los vértices.

Tangente

La forma más simple de determinar la ecuación del tangente en un punto $(x_{0},y_{0})$ es para diferenciar implícitamente la ecuación ${displaystyle {tfrac {x^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1}$ de la hiperbola. Denotación dy/dx como y, esto produce

${displaystyle {frac {2x}{a^{2}}}-{frac {2yy'}{b^{2}}}=0 Rightarrow y'={frac {x}{y}}{frac {b^{2}}{a^{2}}} Rightarrow y={frac {x_{0}}{y_{0}}}{frac {b^{2}}{a^{2}}}(x-x_{0})+y_{0}.}$

Con respecto a ${displaystyle {tfrac {x_{0}^{2}}{a^{2}}}-{tfrac {y_{0}^{2}}{b^{2}}}=1}$ , la ecuación del tangente en el punto $(x_{0},y_{0})$ es

${displaystyle {frac {x_{0}}{a^{2}}}x-{frac {y_{0}}{b^{2}}}y=1.}$

Una línea tangente particular distingue la hipérbola de las otras secciones cónicas. Sea f la distancia desde el vértice V (tanto en la hipérbola como en su eje a través de los dos focos) al foco más cercano. Entonces la distancia, a lo largo de una línea perpendicular a ese eje, desde ese foco hasta un punto P en la hipérbola es mayor que 2f. La tangente a la hipérbola en P interseca ese eje en el punto Q en un ángulo ∠PQV de más de 45°.

Hipérbola rectangular

En el caso $a=b$ la hiperbola se llama rectangular (o equilátero), porque sus asintotos se intersecten en ángulos rectos. Para este caso, la excentricidad lineal es ${displaystyle c={sqrt {2}}a}$ , la excentricidad ${displaystyle e={sqrt {2}}}$ y el recto semi-lato ${displaystyle p=a}$ . El gráfico de la ecuación $y=1/x$ es una hiperbola rectangular.

Representación paramétrica con seno/coseno hiperbólico

Utilizando las funciones de seno hiperbólico y cosino ${displaystyle coshsinh }$ , una representación paramétrica de la hiperbola ${displaystyle {tfrac {x^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1}$ se puede obtener, que es similar a la representación paramétrica de un elipse:

${displaystyle (pm acosh t,bsinh t),,tin mathbb {R} }$

que satisface la ecuación cartesiana porque ${displaystyle cosh ^{2}t-sinh ^{2}t=1.}$

Más representaciones paramétricas se dan en la sección Ecuaciones paramétricas a continuación.

Aquí. a = b = 1 dando a la unidad hiperbola en azul y su hiperbola conjugada en verde, compartiendo los mismos asintotos rojos.

Hipérbola conjugada

Cambio ${displaystyle {frac {x^{2}}{a^{2}}}}$ y ${displaystyle {frac {y^{2}}{b^{2}}}}$ para obtener la ecuación de la conjugar hiperbola (ver diagrama):

${displaystyle {frac {y^{2}}{b^{2}}}-{frac {x^{2}}{a^{2}}}=1}$ también escrito como

${displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=-1.}$

En coordenadas polares

Hyperbola: Coordenadas polares con polo = foco

Hyperbola: Coordenadas polares con poste = centro

Parcela animada de Hyperbola utilizando ${displaystyle r={frac {p}{1-ecos theta }}}$

Para polo = foco:

Las coordenadas polares utilizadas más comúnmente para la hiperbola se definen en relación con el sistema de coordenadas cartesiano que tiene su origin in a focus y su eje x apuntando hacia el origen del "sistema de coordenadas canónicas" como se ilustra en el primer diagrama.
En este caso el ángulo $varphi$ se llama verdadera anomalía.

Relativo a este sistema de coordenadas se tiene que

${displaystyle r={frac {p}{1mp ecos varphi }},quad p={tfrac {b^{2}}{a}}}$

$<math alttext="{displaystyle -arccos left(-{frac {1}{e}}right)<varphi − − arccos⁡ ⁡ ()− − 1e).φ φ .arccos⁡ ⁡ ()− − 1e).{displaystyle - 'arccos left(-{frac {1} {e}}right) Se hizo varphi 'arccos left(-{frac {1} {e}right).<img alt="{displaystyle -arccos left(-{frac {1}{e}}right)<varphi$

para polo = centro:

Con coordenadas polares relativas al "sistema de coordenadas canónicas" (ver segundo diagrama) uno tiene eso

${displaystyle r={frac {b}{sqrt {e^{2}cos ^{2}varphi -1}}}.,}$

Para la rama derecha de la hiperbola el rango de $varphi$ es

$<math alttext="{displaystyle -arccos left({frac {1}{e}}right)<varphi − − arccos⁡ ⁡ ()1e).φ φ .arccos⁡ ⁡ ()1e).{displaystyle -arccos left({frac {1}{e}}right) seleccionóvarphi-traccos left({frac {1}right).}}<img alt="{displaystyle -arccos left({frac {1}{e}}right)<varphi$

Ecuaciones paramétricas

Una hiperbola con ecuación ${displaystyle {tfrac {x^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1}$ puede describirse por varias ecuaciones paramétricas:

${displaystyle {begin{cases}x=pm acosh t,\y=bsinh t,end{cases}}qquad tin mathbb {R}.}$
$0}" xmlns="http://www.w3.org/1998/Math/MathML">{}x=± ± at2+12t,Sí.=bt2− − 12t,t■0{displaystyle {begin{cases}x=pm a{tfrac {fnMicroc} {t^{2}-1}{2t}},end{cases}qquad t título0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bed9d40d9f8b256b5c9fed5eb9854ad259f1e7f0" style="vertical-align: -3.505ex; width:25.038ex; height:8.176ex;"/>$ ()racional representación).
$<math alttext="{displaystyle {begin{cases}x={frac {a}{cos t}}=asec t,\y=pm btan t,end{cases}}qquad 0leq t{}x=a#⁡ ⁡ t=asec⁡ ⁡ t,Sí.=± ± b#⁡ ⁡ t,0≤ ≤ t.2π π ,tل ل π π 2,tل ل 32π π .{displaystyle {begin{cases}x={frac {cos t}=asec t,\y=pm btan t,end{cases}qquad 0leq t made2pi tneq {beq {pi }{2}}, tneq} {3} {2}pi.}<img alt="{displaystyle {begin{cases}x={frac {a}{cos t}}=asec t,\y=pm btan t,end{cases}}qquad 0leq t$
Pendiente tangente como parámetro:
Una representación paramétrica, que utiliza la pendiente $m$ del tangente en un punto de la hiperbola se puede obtener analógicamente al caso elipse: Reemplazar en el caso elipse $b^{2}$ por $-b^{2}$ y utilizar fórmulas para las funciones hiperbólicas. Uno se pone
$b/a.}" xmlns="http://www.w3.org/1998/Math/MathML">c→ → ± ± ()m)=()− − ma2± ± m2a2− − b2,− − b2± ± m2a2− − b2),SilenciomSilencio■b/a.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fnMicroc} {fnMicroc} {fnMicroc} {fnMicrosoft}}{fnMicros}} {fnMicros}} {fnMicrosoft Principiciones}}f}f}}fncipiciones {sqrt {m^{2}a}{2}}} {frac}}} {frac}} {-b^{2}}}}derecha),quad Silencio.b/a.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0175d7bdb9570733715942f4f0c27b6dc1ca1a9d" style="vertical-align: -3.171ex; width:60.896ex; height:7.509ex;"/>$
${displaystyle {vec {c}}_{-}}$ es la parte superior, y ${displaystyle {vec {c}}_{+}}$ la mitad inferior de la hiperbola. Los puntos con tangentes verticales ${displaystyle (pm a,0)}$ ) no están cubiertos por la representación.
La ecuación del tangente en el punto ${vec c}_{pm }(m)$ es
${displaystyle y=mxpm {sqrt {m^{2}a^{2}-b^{2}}}.}$
Esta descripción de los tangentes de una hiperbola es una herramienta esencial para la determinación de la ortoptica de una hiperbola.

Funciones hiperbólicas

Un rayo a través de la unidad hiperbola ${displaystyle x^{2} - y^{2} = 1}$ en el punto ${displaystyle (cosh ,a,,sinh ,a)}$ , donde $a$ es el doble de la zona entre el rayo, la hiperbola, y la $x$ -Eje. Para puntos en la hiperbola debajo del $x$ -eje, el área se considera negativa.

Así como las funciones trigonométricas se definen en términos del círculo unitario, también las funciones hiperbólicas se definen en términos de la hipérbola unitaria, como se muestra en este diagrama. En un círculo unitario, el ángulo (en radianes) es igual al doble del área del sector circular que subtiende ese ángulo. El ángulo hiperbólico análogo se define igualmente como el doble del área de un sector hiperbólico.

Vamos $a$ ser el doble de la zona entre $x$ axis y un rayo a través del origen intersectando la unidad hiperbola, y definir ${textstyle (x,y)=(cosh a,sinh a)=(x,{sqrt {x^{2}-1}})}$ como las coordenadas del punto de intersección. Luego el área del sector hiperbólico es el área del triángulo menos la región curvada por encima del vértice en $(1,0)$ :

${displaystyle {begin{aligned}{frac {a}{2}}&={frac {xy}{2}}-displaystyle int _{1}^{x}{sqrt {t^{2}-1}},dt\&={frac {x{sqrt {x^{2}-1}}}{2}}-{frac {x{sqrt {x^{2}-1}}-ln left(x+{sqrt {x^{2}-1}}right)}{2}},end{aligned}}}$

que se simplifica al coseno hiperbólico del área

${displaystyle a=operatorname {arcosh} x=ln left(x+{sqrt {x^{2}-1}}right).}$

Solving for $x$ produce la forma exponencial de la cosina hiperbólica:

${displaystyle x=cosh a={frac {e^{a}+e^{-a}}{2}}.}$

Desde $x^2-y^2=1$ uno se pone

${displaystyle y=sinh a={sqrt {cosh ^{2}a-1}}={frac {e^{a}-e^{-a}}{2}},}$

y su inversa el área del seno hiperbólico:

${displaystyle a=operatorname {arsinh} y=ln left(y+{sqrt {y^{2}+1}}right).}$

Otras funciones hiperbólicas se definen según el coseno hiperbólico y el seno hiperbólico, así por ejemplo

${displaystyle operatorname {tanh} a={frac {sinh a}{cosh a}}={frac {e^{2a}-1}{e^{2a}+1}}.}$

Propiedades

La tangente biseca el ángulo entre las líneas a los focos

Hyperbola: los bizcoctos tangentes las líneas a través del foci

El tangente en un punto $P$ bisecta el ángulo entre las líneas ${displaystyle {overline {PF_{1}}},{overline {PF_{2}}}}$ .

Prueba

Vamos $L$ ser el punto en la línea ${displaystyle {overline {PF_{2}}}}$ con la distancia $2a$ a la atención $F_{2}$ (ver diagrama, $a$ es el eje semi mayor de la hiperbola). Línea $w$ es el bisector del ángulo entre las líneas ${displaystyle {overline {PF_{1}}},{overline {PF_{2}}}}$ . Para probarlo $w$ es la línea tangente en el punto $P$ , uno verifica que cualquier punto $Q$ on line $w$ que es diferente de $P$ no puede estar en la hiperbola. Por lo tanto $w$ sólo tiene sentido $P$ en común con la hiperbola y es, por lo tanto, el tangente en el punto $P$ .
Desde el diagrama y la desigualdad triángulo uno reconoce que $<math alttext="{displaystyle |QF_{2}|SilencioQF2Silencio.SilencioLF2Silencio+SilencioQLSilencio=2a+SilencioQF1Silencio{displaystyle SilencioQF_{2} detenerse<img alt="{displaystyle |QF_{2}|$ sostiene, lo que significa: $<math alttext="{displaystyle |QF_{2}|-|QF_{1}|SilencioQF2Silencio− − SilencioQF1Silencio.2a{displaystyle TENIENDO:<img alt="{displaystyle |QF_{2}|-|QF_{1}|$ . Pero si $Q$ es un punto de la hiperbola, la diferencia debe ser $2a$ .

Puntos medios de cuerdas paralelas

Hyperbola: los puntos intermedios de los acordes paralelos se encuentran en una línea.

Hyperbola: el punto medio de un acorde es el punto medio del acorde correspondiente de los asintotos.

Los puntos medios de las cuerdas paralelas de una hipérbola se encuentran en una línea que pasa por el centro (ver diagrama).

Los puntos de cualquier cuerda pueden estar en diferentes ramas de la hipérbola.

La prueba de la propiedad en puntos intermedios es mejor hecha para la hiperbola $y=1/x$ . Porque cualquier hiperbola es una imagen afinada de la hiperbola $y=1/x$ (ver sección abajo) y una transformación afinal preserva el paralelismo y los puntos intermedios de segmentos de líneas, la propiedad es verdadera para todas las hiperbolas:
Para dos puntos ${displaystyle P=left(x_{1},{tfrac {1}{x_{1}}}right), Q=left(x_{2},{tfrac {1}{x_{2}}}right)}$ de la hiperbola $y=1/x$

el punto medio del acorde es ${displaystyle M=left({tfrac {x_{1}+x_{2}}{2}},cdots right)=cdots ={tfrac {x_{1}+x_{2}}{2}};left(1,{tfrac {1}{x_{1}x_{2}}}right);}$

la pendiente del acorde es ${displaystyle {frac {{tfrac {1}{x_{2}}}-{tfrac {1}{x_{1}}}}{x_{2}-x_{1}}}=cdots =-{tfrac {1}{x_{1}x_{2}}}.}$

Para acordes paralelos la pendiente es constante y los puntos intermedios de los acordes paralelos se encuentran en la línea ${displaystyle y={tfrac {1}{x_{1}x_{2}}};x.}$

Consecuencia: para cualquier par de puntos $P,Q$ de un acorde existe Reflexión de la sierra con un eje (conjunto de puntos fijos) pasando por el centro de la hiperbola, que intercambia los puntos $P,Q$ y deja la hiperbola (como un todo) fijada. Un reflejo escéptico es una generalización de una reflexión ordinaria a través de una línea $m$ , donde todos los pares de imagen de punto están en una línea perpendicular a $m$ .

Debido a que un reflejo de la mandíbula deja la hiperbola fija, el par de asintotos también se fija. De ahí el punto medio $M$ de un acorde $P Q$ divide el segmento de línea correspondiente ${displaystyle {overline {P}},{overline {Q}}}$ entre los asintotos en las mitades, también. Esto significa que ${displaystyle |P{overline {P}}|=|Q{overline {Q}}|}$ . Esta propiedad se puede utilizar para la construcción de nuevos puntos $Q$ de la hiperbola si un punto $P$ y los asintotos se dan.

Si la cuerda degenera en una tangente, entonces el punto de contacto divide el segmento de línea entre las asíntotas en dos mitades.

Tangentes ortogonales – ortóptica

Hyperbola con su ortoptico (magenta)

Para una hiperbola $b}" xmlns="http://www.w3.org/1998/Math/MathML">x2a2− − Sí.2b2=1,a■b{displaystyle {frac {x^{2}{a^{2}}-{frac} {y^{2}{b^{2}}=1,,a}b}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/79dae9b470b8f2e6d6eeadb9414e3a8dae15b9c8" style="vertical-align: -2.171ex; width:20.119ex; height:6.009ex;"/>$ los puntos de intersección ortogonal tangentes mienten en el círculo $x^{2}+y^{2}=a^{2}-b^{2}$ .
Este círculo se llama ortoptico de la hiperbola dada.

Las tangentes pueden pertenecer a puntos en diferentes ramas de la hipérbola.

En caso de $aleq b$ No hay pares de tangentes ortogonales.

Relación polo-polar para una hipérbola

Hiperbola: relación post-polar

Cualquier hiperbola se puede describir en un sistema de coordenadas adecuado por una ecuación ${displaystyle {tfrac {x^{2}}{a^{2}}}-{tfrac {y^{2}}{b^{2}}}=1}$ . La ecuación del tangente en un punto ${displaystyle P_{0}=(x_{0},y_{0})}$ de la hiperbola es ${displaystyle {tfrac {x_{0}x}{a^{2}}}-{tfrac {y_{0}y}{b^{2}}}=1.}$ Si uno permite el punto ${displaystyle P_{0}=(x_{0},y_{0})}$ ser un punto arbitrario diferente del origen, entonces

punto ${displaystyle P_{0}=(x_{0},y_{0})neq (0,0)}$ se mapea en la línea ${displaystyle {frac {x_{0}x}{a^{2}}}-{frac {y_{0}y}{b^{2}}}=1}$ , no a través del centro de la hiperbola.

Esta relación entre puntos y líneas es una biyección.

Los mapas de funciones inversas

línea ${displaystyle y=mx+d, dneq 0}$ sobre el punto ${displaystyle left(-{frac {ma^{2}}{d}},-{frac {b^{2}}{d}}right)}$ y

línea ${displaystyle x=c, cneq 0}$ sobre el punto ${displaystyle left({frac {a^{2}}{c}},0right).}$

Tal relación entre puntos y líneas generada por una cónica se llama relación polo-polar o simplemente polaridad. El polo es el punto, el polar la línea. Véase Polo y polar.

Mediante el cálculo se comprueban las siguientes propiedades de la relación polo-polar de la hipérbola:

Para un punto (pole) on el hiperbola el polar es el tangente en este punto (ver diagrama: ${displaystyle P_{1}, p_{1}}$ ).
Para un poste $P$ afuera la hiperbola los puntos de intersección de su polar con la hiperbola son los puntos de tangencia de los dos tangentes que pasan $P$ (ver diagrama: ${displaystyle P_{2}, p_{2}, P_{3}, p_{3}}$ ).
Para un punto dentro la hiperbola el polar no tiene sentido con la hiperbola en común. (ver diagrama: ${displaystyle P_{4}, p_{4}}$ ).

Observaciones:

El punto de intersección de dos polares (por ejemplo: ${displaystyle p_{2},p_{3}}$ ) es el polo de la línea a través de sus polos (aquí: ${displaystyle P_{2},P_{3}}$ ).
El foci ${displaystyle (c,0),}$ y ${displaystyle (-c,0)}$ respectivamente y las directrices ${displaystyle x={tfrac {a^{2}}{c}}}$ y ${displaystyle x=-{tfrac {a^{2}}{c}}}$ respectivamente pertenecen a pares de polos y polares.

También existen relaciones polo-polares para elipses y parábolas.

Otras propiedades

Los siguientes son concurrentes: (1) un círculo que pasa por el foci de la hiperbola y se centra en el centro de la hiperbola; (2) cualquiera de las líneas que son tangente a la hiperbola en los vértices; y (3) cualquiera de los asintotos de la hiperbola.
Los siguientes son también concurrentes: (1) el círculo que se centra en el centro de la hiperbola y que pasa a través de los vértices de la hiperbola; (2) ya sea directrix; y (3) cualquiera de los asintotos.

Longitud de arco

La longitud de arco de una hipérbola no tiene una expresión elemental. La mitad superior de una hipérbola se puede parametrizar como

${displaystyle y=b{sqrt {{frac {x^{2}}{a^{2}}}-1}}.}$

Luego la integral dando la longitud del arco $s$ desde $x_{1}$ a $x_{2}$ puede ser calculado como:

${displaystyle s=bint _{operatorname {arcosh} {frac {x_{1}}{a}}}^{operatorname {arcosh} {frac {x_{2}}{a}}}{sqrt {1+left(1+{frac {a^{2}}{b^{2}}}right)sinh ^{2}v}},mathrm {d} v.}$

Después de utilizar la sustitución ${displaystyle z=iv}$ , esto también puede ser representado usando la integral elíptica incompleta del segundo tipo $E$ con parámetro ${displaystyle m=k^{2}}$ :

${displaystyle s=ib{Biggr [}Eleft(iv,{Biggr |},1+{frac {a^{2}}{b^{2}}}right){Biggr ]}_{operatorname {arcosh} {frac {x_{2}}{a}}}^{operatorname {arcosh} {frac {x_{1}}{a}}}.}$

Usando solo números reales, esto se convierte en

${displaystyle s=bleft[Fleft(operatorname {gd} v,{Biggr |}-{frac {a^{2}}{b^{2}}}right)-Eleft(operatorname {gd} v,{Biggr |}-{frac {a^{2}}{b^{2}}}right)+{sqrt {1+{frac {a^{2}}{b^{2}}}tanh ^{2}v}},sinh vright]_{operatorname {arcosh} {tfrac {x_{1}}{a}}}^{operatorname {arcosh} {tfrac {x_{2}}{a}}}}$

Donde $F$ es la integral elíptica incompleta del primer tipo con parámetro ${displaystyle m=k^{2}}$ y ${displaystyle operatorname {gd} v=arctan sinh v}$ es la función Gudermanniana.

Curvas derivadas

espirales sinusoidales ( $r n = 1 n Porque... No.), Silencio = π /2$ ) en coordenadas polares y sus equivalentes en coordenadas rectangulares:
$n = 2$ : Hiperbola equivalente

$n = 1 -$ : Línea

$n = 1/2$ : Parabola

$n = 1/2$ : Cardioide

$n = 1$ : Círculo

$n = 2$ : Lemniscate de Bernoulli

Varias otras curvas pueden derivarse de la hipérbola por inversión, las llamadas curvas inversas de la hipérbola. Si se elige como centro de inversión el propio centro de la hipérbola, la curva inversa es la lemniscata de Bernoulli; la lemniscata es también la envolvente de círculos con centro en una hipérbola rectangular y que pasa por el origen. Si el centro de inversión se elige en un foco o en un vértice de la hipérbola, las curvas inversas resultantes son una limaçon o una estrofoide, respectivamente.

Coordenadas elípticas

Una familia de hipérbolas confocales es la base del sistema de coordenadas elípticas en dos dimensiones. Estas hipérbolas se describen mediante la ecuación

${displaystyle left({frac {x}{ccos theta }}right)^{2}-left({frac {y}{csin theta }}right)^{2}=1}$

donde los focos están ubicados a una distancia c del origen en el eje x, y donde θ es el ángulo de las asíntotas con la x -eje. Cada hipérbola en esta familia es ortogonal a cada elipse que comparte los mismos focos. Esta ortogonalidad puede mostrarse mediante un mapa conforme del sistema de coordenadas cartesianas w = z + 1/z, donde z= x + iy son las coordenadas cartesianas originales, y w=u + iv son los que siguen a la transformación.

Otros sistemas de coordenadas bidimensionales ortogonales que involucran hipérbolas se pueden obtener mediante otras asignaciones conformes. Por ejemplo, la aplicación w = z² transforma el sistema de coordenadas cartesianas en dos familias de hipérbolas ortogonales.

Análisis de sección cónica de la apariencia hiperbólica de círculos

Proyección central de círculos en una esfera: El centro O de proyección está dentro de la esfera, el plano de imagen es rojo.
Como imágenes de los círculos se obtiene un círculo (magenta), elipses, hiperbolas y líneas. El caso especial de una parabola no aparece en este ejemplo.
(Si centro O eran on la esfera, todas las imágenes de los círculos serían círculos o líneas; ver proyección estereográfica).

Además de proporcionar una descripción uniforme de círculos, elipses, parábolas e hipérbolas, las secciones cónicas también pueden entenderse como un modelo natural de la geometría de la perspectiva en el caso de que la escena que se está viendo consista en círculos o, más generalmente, en una elipse.. El espectador suele ser una cámara o el ojo humano y la imagen de la escena es una proyección central sobre un plano de imagen, es decir, todos los rayos de proyección pasan por un punto fijo O, el centro. El plano de la lente es un plano paralelo al plano de la imagen en la lente O.

La imagen de un círculo c es

a) a círculo, si círculo c está en una posición especial, por ejemplo paralela al plano de imagen y otros (ver proyección estereográfica),

b) un elipse, si c tiene no punto con el plano de la lente en común,

c) a parabola, si c tiene uno punto con el plano de la lente en común

d) a hiperbola, si c tiene dos. puntos con el plano de la lente en común.

(Se omiten las posiciones especiales donde el plano del círculo contiene el punto O).

Estos resultados se pueden entender si se reconoce que el proceso de proyección se puede ver en dos pasos: 1) el círculo c y el punto O generan un cono que es 2) cortado por el plano de la imagen, en para generar la imagen.

Uno ve una hipérbola cada vez que ve una parte de un círculo cortado por el plano de la lente. La incapacidad de ver gran parte de los brazos de la rama visible, combinada con la ausencia total de la segunda rama, hace que sea prácticamente imposible que el sistema visual humano reconozca la conexión con las hipérbolas.

Aplicaciones

Hyperbolas como líneas de declinación en un sundial

La zona de contacto de la onda de choque de un avión supersónico de nivel en tierra plana (amarillo) es parte de una hiperbola ya que el suelo interseca el cono paralelo a su eje

Relojes de sol

Las hipérbolas se pueden ver en muchos relojes de sol. En un día cualquiera, el sol gira en un círculo en la esfera celeste, y sus rayos golpeando el punto de un reloj de sol trazan un cono de luz. La intersección de este cono con el plano horizontal del suelo forma una sección cónica. En latitudes más pobladas y en la mayoría de las épocas del año, esta sección cónica es una hipérbola. En términos prácticos, la sombra de la punta de un poste traza una hipérbola en el suelo a lo largo de un día (este camino se llama línea de declinación). La forma de esta hipérbola varía con la latitud geográfica y con la época del año, ya que esos factores afectan el cono de los rayos del sol en relación con el horizonte. Los griegos llamaban pelekinon a la colección de tales hipérbolas durante un año entero en un lugar determinado, ya que se asemeja a un hacha de doble hoja.

Multilateración

Una hipérbola es la base para resolver problemas de multilateración, la tarea de ubicar un punto a partir de las diferencias en sus distancias a puntos dados o, de manera equivalente, la diferencia en tiempos de llegada de señales sincronizadas entre el punto y los puntos dados. Tales problemas son importantes en la navegación, particularmente en el agua; un barco puede ubicar su posición a partir de la diferencia en los tiempos de llegada de las señales de un transmisor LORAN o GPS. Por el contrario, una baliza de búsqueda o cualquier transmisor se puede ubicar comparando los tiempos de llegada de sus señales en dos estaciones receptoras separadas; tales técnicas pueden usarse para rastrear objetos y personas. En particular, el conjunto de posiciones posibles de un punto que tiene una diferencia de distancia de 2a de dos puntos dados es una hipérbola de separación de vértice 2a cuyos focos son los dos puntos dados.

Camino seguido por una partícula

La trayectoria seguida por cualquier partícula en el problema clásico de Kepler es una sección cónica. En particular, si la energía total E de la partícula es mayor que cero (es decir, si la partícula no está ligada), la trayectoria de tal partícula es una hipérbola. Esta propiedad es útil para estudiar las fuerzas atómicas y subatómicas mediante la dispersión de partículas de alta energía; por ejemplo, el experimento de Rutherford demostró la existencia de un núcleo atómico al examinar la dispersión de partículas alfa de los átomos de oro. Si se ignoran las interacciones nucleares de corto alcance, el núcleo atómico y la partícula alfa interactúan solo por una fuerza de Coulomb repulsiva, lo que satisface el requisito de la ley del inverso del cuadrado para un problema de Kepler.

Ecuación de Korteweg-de Vries

Función de trig hiperbólica $operatorname{sech}, x$ aparece como una solución a la ecuación Korteweg-de Vries que describe el movimiento de una onda solitona en un canal.

Trisección de ángulo

Trisecando un ángulo (AOB) usando una hiperbola de excentricidad 2 (curva amarilla)

Como se muestra primero por Apolonio de Perga, una hiperbola se puede utilizar para trisectar cualquier ángulo, un problema bien estudiado de la geometría. Dado un ángulo, primero dibuja un círculo centrado en su vértice O, que intersecte los lados del ángulo en los puntos A y B. Siguiente dibujar el segmento de línea con puntos finales A y B y su bisector perpendicular $ell$ . Construir una hiperbola de excentricidad e=2 con $ell$ como directrix y B como enfoque. Vamos P ser la intersección (upper) de la hiperbola con el círculo. Angle POB ángulo de trisectos AOB.

Para demostrarlo, refleje el segmento de línea OP sobre la línea $ell$ obtener el punto P ' como la imagen de P. Segmento AP' tiene la misma longitud que el segmento BP debido a la reflexión, mientras segmento PP' tiene la misma longitud que el segmento BP debido a la excentricidad de la hiperbola. As OA, OP ', OP y OB son todos los radios del mismo círculo (y así, tienen la misma longitud), los triángulos OAP ', OPP ' y OPB son todos congruentes. Por lo tanto, el ángulo ha sido trisecado, desde 3×POB = AOB.

Frontera de cartera eficiente

En la teoría de carteras, el lugar geométrico de las carteras eficientes de varianza media (llamada frontera eficiente) es la mitad superior de la rama de apertura este de una hipérbola dibujada con la desviación estándar del rendimiento de la cartera trazada horizontalmente y su valor esperado. valor trazado verticalmente; según esta teoría, todos los inversores racionales elegirían una cartera caracterizada por algún punto de este locus.

Bioquímica

En bioquímica y farmacología, la ecuación de Hill y la ecuación de Hill-Langmuir describen, respectivamente, respuestas biológicas y la formación de complejos proteína-ligando en función de la concentración de ligando. Ambas son hipérbolas rectangulares.

Las hipérbolas como secciones planas de cuádricas

Las hipérbolas aparecen como secciones planas de las siguientes cuádricas:

Elliptic cone
Cilindro hiperbólico
Paraboloide hiperbólico
Hiperboloide de una hoja
Hiperboloide de dos hojas

Elliptic cone
Cilindro hiperbólico
Paraboloide hiperbólico
Hiperboloide de una hoja
Hiperboloide de dos hojas

Contenido relacionado

Grupo fundamental
NP (complejidad)
Extensión de campo
Más resultados...
Te puede interesar