Hexominó

Un hexominó (o 6-omino) es un poliominó de orden 6, es decir, un polígono en el plano formado por 6 cuadrados del mismo tamaño conectados por los bordes. hasta el borde. El nombre de este tipo de figuras se forma con el prefijo hex(a)-. Cuando las rotaciones y las reflexiones no se consideran formas distintas, hay 35 hexominós libres diferentes. Cuando las reflexiones se consideran distintas, hay 60 hexominós unilaterales. Cuando las rotaciones también se consideran distintas, hay 216 hexominós fijos.

Simetría

La figura anterior muestra los 35 hexominós libres posibles, coloreados según sus grupos de simetría:

• Los veinte hexominos grises no tienen simetría. Su grupo de simetría consiste sólo en el mapeo de identidad.
• Los seis hexominos rojos tienen un eje de simetría espejo paralelo a las líneas de rejilla. Su grupo de simetría tiene dos elementos, la identidad y una reflexión en una línea paralela a los lados de los cuadrados.
• Los dos hexominos verdes tienen un eje de simetría de espejo a 45° a las líneas de red. Su grupo de simetría tiene dos elementos, la identidad y una reflexión diagonal.
• Los cinco hexominos azules tienen simetría de puntos, también conocida como simetría rotacional del orden 2. Su grupo de simetría tiene dos elementos, la identidad y la rotación de 180°.
• Los dos hexominos púrpuras tienen dos ejes de simetría espejo, ambos paralelos a las líneas de rejilla (por ejemplo, un eje horizontal y un eje vertical). Su grupo de simetría tiene cuatro elementos. Es el grupo dihedral de orden 2, también conocido como el grupo Klein cuatro.

Si los reflejos de un hexominó se consideran distintos, como lo son con los hexominós unilaterales, entonces la primera y la cuarta categoría anteriores duplicarían su tamaño, lo que daría como resultado 25 hexominós adicionales para un total de 60. Si las rotaciones también se se consideran distintos, entonces los hexominós de la primera categoría cuentan ocho veces, los de las siguientes tres categorías cuentan cuatro veces y los de la última categoría cuentan dos veces. Esto da como resultado 20 × 8 + (6 + 2 + 5) × 4 + 2 × 2 = 216 hexominós fijos.

Embalaje y mosaico

Cada uno de los 35 hexominós satisface el criterio de Conway; por tanto, cada hexomino es capaz de enlosar el plano.

Aunque un juego completo de 35 hexominós tiene un total de 210 cuadrados, no es posible empaquetarlos en un rectángulo. (Tal disposición es posible con los 12 pentominós que se pueden empaquetar en cualquiera de los rectángulos 3 × 20, 4 × 15, 5 × 12 y 6 × 10.) Una forma sencilla de demostrar que tal empaquetamiento de hexominós no es posible. es a través de un argumento de paridad. Si los hexominós se colocan en un patrón de tablero de ajedrez, entonces 11 de los hexominós cubrirán un número par de cuadrados negros (ya sea 2 blancos y 4 negros o viceversa) y los otros 24 hexominós cubrirán un número impar de cuadrados negros (3 blancos). y 3 negros). En general, en cualquier disposición se cubrirá un número par de cuadrados negros. Sin embargo, cualquier rectángulo de 210 cuadrados tendrá 105 cuadrados negros y 105 cuadrados blancos y, por lo tanto, no puede estar cubierto por los 35 hexominós.

Sin embargo, existen otras figuras simples de 210 cuadrados que se pueden empaquetar con los hexominós. Por ejemplo, un cuadrado de 15 × 15 al que se le quita un rectángulo de 3 × 5 del centro tiene 210 cuadrados. Con el color del tablero de ajedrez, tiene 106 cuadrados blancos y 104 negros (o viceversa), por lo que la paridad no impide un empaque, y un empaque es realmente posible. También es posible que dos conjuntos de piezas quepan en un rectángulo de tamaño 420, o que el conjunto de 60 hexominós de un lado (18 de los cuales cubren un número par de cuadrados negros) quepan en un rectángulo de tamaño 360.

Redes poliédricas para el cubo

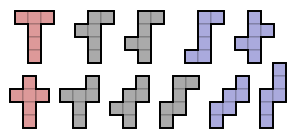
Una red poliédrica para el cubo es necesariamente un hexominó, y 11 hexominós (que se muestran a la derecha) son en realidad redes. Aparecen a la derecha, nuevamente coloreados según sus grupos de simetría.

Una red poliédrica para el cubo no puede contener el O-tetromino, ni el I-pentomino, el U-pentomino, ni el V-pentomino.