Heredabilidad
Heredabilidad es una estadística utilizada en los campos de la cría y la genética que estima el grado de variación en un rasgo fenotípico en una población que se debe a la variación genética entre individuos. en esa población. El concepto de heredabilidad se puede expresar en la forma de la siguiente pregunta: "¿Cuál es la proporción de la variación en un rasgo dado dentro de una población que no se explica por el medio ambiente o el azar? ?"
Otras causas de variación medida en un rasgo se caracterizan como factores ambientales, incluido el error de observación. En los estudios de heredabilidad en humanos, a menudo se distribuyen en factores de "entorno compartido" y "entorno no compartido" en función de si tienden a dar lugar a que las personas criadas en el mismo hogar sean más o menos similares a las personas que no lo fueron.
La heredabilidad se estima comparando la variación fenotípica individual entre individuos relacionados en una población, examinando la asociación entre el fenotipo individual y los datos del genotipo, o incluso modelando datos de nivel de resumen de estudios de asociación del genoma completo (GWAS). La heredabilidad es un concepto importante en la genética cuantitativa, particularmente en la crianza selectiva y la genética del comportamiento (por ejemplo, estudios de gemelos). Es fuente de mucha confusión debido al hecho de que su definición técnica es diferente de su definición popular comúnmente entendida. Por lo tanto, su uso transmite la impresión incorrecta de que los rasgos de comportamiento son "heredados" o específicamente transmitido a través de los genes. Los genetistas conductuales también realizan análisis de heredabilidad basados en la suposición de que los genes y los entornos contribuyen de manera separada y aditiva a los rasgos conductuales.
Resumen
La heredabilidad mide la fracción de la variabilidad del fenotipo que se puede atribuir a la variación genética. Esto no es lo mismo que decir que esta fracción de un fenotipo individual es causada por la genética. Por ejemplo, es incorrecto decir que, dado que la heredabilidad de los rasgos de personalidad es de aproximadamente 0,6, eso significa que el 60 % de su personalidad se hereda de sus padres y el 40 % proviene del entorno. Además, la heredabilidad puede cambiar sin que ocurra ningún cambio genético, como cuando el entorno comienza a contribuir a una mayor variación. Como ejemplo, considere que tanto los genes como el entorno tienen el potencial de influir en la inteligencia. La heredabilidad podría aumentar si aumenta la variación genética, haciendo que los individuos muestren más variación fenotípica, como mostrar diferentes niveles de inteligencia. Por otro lado, la heredabilidad también podría aumentar si la variación ambiental disminuye, lo que hace que los individuos muestren menos variación fenotípica, como mostrar niveles de inteligencia más similares. La heredabilidad aumenta cuando la genética contribuye a una mayor variación o porque los factores no genéticos contribuyen a una menor variación; lo que importa es la contribución relativa. La heredabilidad es específica de una población particular en un entorno particular. La alta heredabilidad de un rasgo, en consecuencia, no significa necesariamente que el rasgo no sea muy susceptible a las influencias ambientales. La heredabilidad también puede cambiar como resultado de cambios en el medio ambiente, la migración, la consanguinidad o la forma en que se mide la heredabilidad en la población en estudio. La heredabilidad de un rasgo no debe interpretarse como una medida de la medida en que dicho rasgo está determinado genéticamente en un individuo.
El grado de dependencia del fenotipo del entorno también puede ser una función de los genes implicados. Las cuestiones de heredabilidad son complicadas porque los genes pueden canalizar un fenotipo, haciendo que su expresión sea casi inevitable en todos los entornos que se presenten. Los individuos con el mismo genotipo también pueden exhibir diferentes fenotipos a través de un mecanismo llamado plasticidad fenotípica, que hace que la heredabilidad sea difícil de medir en algunos casos. Conocimientos recientes en biología molecular han identificado cambios en la actividad transcripcional de genes individuales asociados con cambios ambientales. Sin embargo, existe un gran número de genes cuya transcripción no se ve afectada por el entorno.
Las estimaciones de heredabilidad utilizan análisis estadísticos para ayudar a identificar las causas de las diferencias entre individuos. Dado que la heredabilidad se relaciona con la varianza, es necesariamente una explicación de las diferencias entre los individuos de una población. La heredabilidad puede ser univariada, examinando un solo rasgo, o multivariada, examinando las asociaciones genéticas y ambientales entre múltiples rasgos a la vez. Esto permite una prueba de la superposición genética entre diferentes fenotipos: por ejemplo, color de cabello y color de ojos. El medio ambiente y la genética también pueden interactuar, y los análisis de heredabilidad pueden probar y examinar estas interacciones (modelos GxE).
Un requisito previo para los análisis de heredabilidad es que haya que tener en cuenta alguna variación de la población. Este último punto destaca el hecho de que la heredabilidad no puede tener en cuenta el efecto de factores que son invariantes en la población. Los factores pueden ser invariantes si están ausentes y no existen en la población, como que nadie tenga acceso a un antibiótico en particular, o porque están omnipresentes, como si todos estuvieran bebiendo café. En la práctica, todos los rasgos del comportamiento humano varían y casi todos los rasgos muestran cierta heredabilidad.
Definición
Cualquier fenotipo particular se puede modelar como la suma de los efectos genéticos y ambientales:
- FenotipoP) = Genotipo (G) + Medio ambienteE).
Del mismo modo, la variación fenotípica en el rasgo, Var (P), es la suma de los efectos de la siguiente manera:
- Var(P) = Var(G) + Var(E) + 2 Cov(G,E).
En un experimento planeado Cov(G,E) se puede controlar y mantener a 0. En este caso, heribilidad, H2,{displaystyle H^{2},} se define como
- H2=Var()G)Var()P){displaystyle ¿Qué?
H2 es la heredabilidad en sentido amplio. Esto refleja todas las contribuciones genéticas a la variación fenotípica de una población, incluidas las aditivas, dominantes y epistáticas (interacciones multigénicas), así como los efectos maternos y paternos, donde los individuos se ven afectados directamente por la influencia de sus padres. fenotipo, como la producción de leche en los mamíferos.
Un componente particularmente importante de la variación genética es la variación aditiva, Var(A), que es la variación debida a los efectos promedio (efectos aditivos) de los alelos. Dado que cada progenitor transmite un único alelo por locus a cada descendiente, el parecido entre progenitores e hijos depende del efecto medio de los alelos individuales. La varianza aditiva representa, por lo tanto, el componente genético de la varianza responsable del parecido entre padres e hijos. La porción genética aditiva de la variación fenotípica se conoce como heredabilidad en sentido estricto y se define como
- h2=Var()A)Var()P){displaystyle ¿Qué?
Se usa una H2 mayúscula para denotar un sentido amplio y una h2 minúsculas para un sentido estrecho. sentido.
Para rasgos que no son continuos sino dicotómicos, como un dedo del pie adicional o ciertas enfermedades, la contribución de varios alelos se puede considerar como una suma, que más allá de un umbral, se manifiesta como el rasgo, dando el modelo de umbral de responsabilidad en el que se puede estimar la heredabilidad y modelar la selección.
La varianza aditiva es importante para la selección. Si se ejerce una presión selectiva como mejorar el ganado, la respuesta del rasgo está directamente relacionada con la heredabilidad en sentido estricto. La media del rasgo aumentará en la próxima generación en función de cuánto difiere la media de los padres seleccionados de la media de la población de la que se eligieron los padres seleccionados. La respuesta a la selección observada conduce a una estimación de la heredabilidad en sentido estricto (llamada heredabilidad realizada). Este es el principio que subyace a la selección o reproducción artificial.
Ejemplo
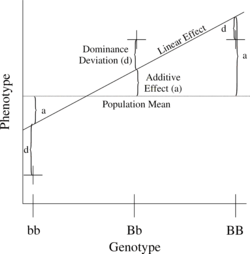
El modelo genético más simple involucra un solo locus con dos alelos (b y B) que afectan un fenotipo cuantitativo.
El número de alelos B puede ser 0, 1 o 2. Para cualquier genotipo, (Bi,B j), donde Bi y Bj son 0 o 1, el fenotipo esperado se puede escribir como la suma de la media general, un efecto lineal y una desviación de dominancia (se puede pensar en el término de dominancia como una interacción entre B i y Bj):
Pij=μ μ +α α ()Bi+Bj)+δ δ ()BiBj)=Población media+Efecto aditivo()aij=α α ()Bi+Bj))+Desviación de la remoción de minas()dij=δ δ ()BiBj)).{displaystyle {begin{aligned}P_{ij} +alpha ,(B_{i}+B_{j})+delta ,(B_{i}B_{j})\ {fnMicrosoft Sans Serif}(a_{ij}=alpha (B_{i}+B_{j})+{text{Dominance Desviación.
La variación genética aditiva en este locus es el promedio ponderado de los cuadrados de los efectos aditivos:
- Var()A)=f()bb)abb2+f()Bb)aBb2+f()BB)aBB2,{displaystyle mathrm {Var} (A)=f(bb)a_{bb}{2}+f(Bb)a_{Bb}{2}+f(BB)a_{2}}}
Donde f()bb)abb+f()Bb)aBb+f()BB)aBB=0.{displaystyle f(bb)a_{bb}+f(Bb)a_{Bb}+f(BB)a_{BB}=0.}
Existe una relación similar para la varianza de las desviaciones de dominancia:
- Var()D)=f()bb)dbb2+f()Bb)dBb2+f()BB)dBB2,{displaystyle mathrm {Var} (D)=f(bb)d_{bb}{2}+f(Bb)d_{Bb}{2}+f(BB)d_{2}}}}
Donde f()bb)dbb+f()Bb)dBb+f()BB)dBB=0.{displaystyle f(bb)d_{bb}+f(Bb)d_{Bb}+f(BB)d_{BB}=0.}
La regresión lineal de fenotipo sobre genotipo se muestra en la Figura 1.
Supuestos
Las estimaciones de la heredabilidad total de los rasgos humanos asumen la ausencia de epistasis, lo que se ha denominado "suposición de aditividad". Aunque algunos investigadores han citado tales estimaciones en apoyo de la existencia de "heredabilidad faltante" no contabilizado por loci genéticos conocidos, la suposición de aditividad puede invalidar estas estimaciones. También hay alguna evidencia empírica de que la suposición de aditividad se viola con frecuencia en los estudios de genética del comportamiento de la inteligencia y el rendimiento académico de los adolescentes.
Estimación de la heredabilidad
Dado que solo P puede observarse o medirse directamente, la heredabilidad debe estimarse a partir de las similitudes observadas en sujetos que varían en su nivel de similitud genética o ambiental. Los análisis estadísticos necesarios para estimar los componentes genéticos y ambientales de la varianza dependen de las características de la muestra. Brevemente, se obtienen mejores estimaciones utilizando datos de individuos con niveles de parentesco genético muy variados, como gemelos, hermanos, padres e hijos, en lugar de sujetos con una relación más lejana (y, por lo tanto, menos similar). El error estándar para las estimaciones de heredabilidad se mejora con muestras de gran tamaño.
En poblaciones no humanas, a menudo es posible recopilar información de forma controlada. Por ejemplo, entre los animales de granja es fácil hacer arreglos para que un toro produzca descendencia de un gran número de vacas y controle los ambientes. Por lo general, dicho control experimental no es posible cuando se recopilan datos humanos, ya que se basan en relaciones y entornos naturales.
En la genética cuantitativa clásica, había dos escuelas de pensamiento con respecto a la estimación de la heredabilidad.
Una escuela de pensamiento fue desarrollada por Sewall Wright en la Universidad de Chicago y popularizada aún más por C. C. Li (Universidad de Chicago) y J. L. Lush (Universidad Estatal de Iowa). Se basa en el análisis de correlaciones y, por extensión, de regresión. Path Analysis fue desarrollado por Sewall Wright como una forma de estimar la heredabilidad.
El segundo fue desarrollado originalmente por R. A. Fisher y se expandió en la Universidad de Edimburgo, la Universidad Estatal de Iowa y la Universidad Estatal de Carolina del Norte, así como en otras escuelas. Se basa en el análisis de varianza de estudios de crianza, utilizando la correlación intraclase de parientes. En estos análisis se utilizan varios métodos para estimar los componentes de la varianza (y, por lo tanto, la heredabilidad) de ANOVA.
Hoy en día, la heredabilidad se puede estimar a partir de genealogías generales utilizando modelos mixtos lineales y de la relación genómica estimada a partir de marcadores genéticos.
Los estudios de heredabilidad humana a menudo utilizan diseños de estudio de adopción, a menudo con gemelos idénticos que se separaron temprano en la vida y se criaron en entornos diferentes. Dichos individuos tienen genotipos idénticos y pueden usarse para separar los efectos del genotipo y el ambiente. Un límite de este diseño es el entorno prenatal común y el número relativamente bajo de gemelos criados por separado. Un segundo y más común diseño es el estudio de gemelos en el que se usa la similitud de gemelos idénticos y mellizos para estimar la heredabilidad. Estos estudios pueden estar limitados por el hecho de que los gemelos idénticos no son completamente idénticos genéticamente, lo que podría resultar en una subestimación de la heredabilidad.
En estudios de observación, o debido a los efectos evocativos (donde un genoma evoca entornos por su efecto sobre ellos), G y E pueden covariar: correlación entre genes y entornos. Según los métodos utilizados para estimar la heredabilidad, las correlaciones entre los factores genéticos y los entornos compartidos o no compartidos pueden o no confundirse con la heredabilidad.
Métodos de estimación de regresión/correlación
La primera escuela de estimación utiliza la regresión y la correlación para estimar la heredabilidad.
Comparación de parientes cercanos
En la comparación de parientes, encontramos que en general,
- h2=br=tr{displaystyle h^{2}={frac {b} {r}={frac} {} {}}}
donde r se puede considerar como el coeficiente de relación, b es el coeficiente de regresión y t es el coeficiente de correlación.
Regresión padre-hijo
La heredabilidad se puede estimar comparando los rasgos de los padres y los descendientes (como en la Fig. 2). La pendiente de la línea (0,57) se aproxima a la heredabilidad del rasgo cuando los valores de la descendencia se comparan con el rasgo promedio de los padres. Si solo se usa el valor de uno de los padres, la heredabilidad es el doble de la pendiente. (Tenga en cuenta que esta es la fuente del término "regresión", ya que los valores de descendencia siempre tienden a retroceder al valor medio de la población, es decir,, la pendiente siempre es menor de una). Este efecto de regresión también subyace en el método DeFries-Fulker para analizar gemelos seleccionados para un miembro afectado.
Comparación entre hermanos
Se puede adoptar un enfoque básico de la heredabilidad utilizando diseños de hermanos completos: comparar la similitud entre hermanos que comparten una madre y un padre biológicos. Cuando solo hay una acción genética aditiva, esta correlación fenotípica entre hermanos es un índice de familiaridad: la suma de la mitad de la variación genética aditiva más el efecto total del entorno común. Por lo tanto, establece un límite superior en la heredabilidad aditiva del doble de la correlación fenotípica de Sib completo. Los diseños de medios hermanos comparan los rasgos fenotípicos de los hermanos que comparten un padre con otros grupos de hermanos.
Estudios de gemelos
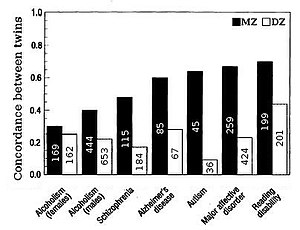
La heredabilidad de los rasgos en humanos se estima con mayor frecuencia comparando las semejanzas entre gemelos. "La ventaja de los estudios de gemelos es que la varianza total se puede dividir en componentes genéticos, ambientales compartidos o comunes y ambientales únicos, lo que permite una estimación precisa de la heredabilidad". Los gemelos fraternos o dicigóticos (DZ) en promedio comparten la mitad de sus genes (suponiendo que no haya apareamiento selectivo para el rasgo), por lo que los gemelos idénticos o monocigóticos (MZ) en promedio son dos veces más similares genéticamente que los gemelos DZ. Entonces, una estimación aproximada de la heredabilidad es aproximadamente el doble de la diferencia en la correlación entre gemelos MZ y DZ, es decir, la fórmula de Falconer H2=2(r(MZ)-r(DZ)).
El efecto del entorno compartido, c2, contribuye a la similitud entre hermanos debido a la similitud del entorno en el que se crían. El entorno compartido se aproxima mediante la DZ correlación menos la mitad de la heredabilidad, que es el grado en que los gemelos DZ comparten los mismos genes, c2=DZ-1/2h2. La variación ambiental única, e2, refleja el grado en que los gemelos idénticos criados juntos son diferentes, e2= 1-r(MZ).
Análisis de varianza métodos de estimación
El segundo conjunto de métodos de estimación de la heredabilidad implica ANOVA y la estimación de los componentes de la varianza.
Modelo básico
Usamos la discusión básica de Kempthorne. Considerando solo los modelos genéticos más básicos, podemos ver la contribución cuantitativa de un solo locus con el genotipo Gi como
- Sí.i=μ μ +gi+e{displaystyle Y... +g_{i}+e}
Donde gi{displaystyle g_{i} es el efecto del genotipo Gi y e{displaystyle e} es el efecto ambiental.
Considere un experimento con un grupo de toros y su progenie de madres aleatorias. Dado que la progenie obtiene la mitad de sus genes del padre y la otra mitad de su madre (aleatoria), la ecuación de la progenie es
- zi=μ μ +12gi+e{displaystyle z_{i}=mu +{frac {1}{2}g_{i}+e}
Correlaciones intraclase
Considere el experimento anterior. Tenemos dos grupos de progenie que podemos comparar. El primero es comparar las diversas progenies de un toro individual (llamado dentro del grupo de toros). La varianza incluirá términos para la varianza genética (ya que no todos obtuvieron el mismo genotipo) y la varianza ambiental. Esto se considera un término de error.
El segundo grupo de progenie son comparaciones de medias de medios hermanos entre sí (llamadas entre grupos de padres). Además del término de error como en los grupos de toros internos, tenemos un término adicional debido a las diferencias entre las diferentes medias de medios hermanos. La correlación intraclase es
- corr()z,z.)=corr()μ μ +12g+e,μ μ +12g+e.)=14Vg{displaystyle mathrm {corr} (z,z')=mathrm {corr} (mu +{frac {1}{2}}g+e,mu +{frac {1} {2}g+e')={frac {1}{4}}V_{g}}} {}} {} {}}} {} {}}} {}} {}}}} {}}}}} {}}}}} {}}}}}} {}}} {}}} {}}}}} {} {}}}}}}}} {}}}}} {}}}}}}}}}}}} {} {}}}}} {}} {} {}}}}}}}} {}}} {}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}} {}}}}} {}}}}}}}}}}
ya que los efectos ambientales son independientes entre sí.
La ANOVA
(feminine)En un experimento con n{displaystyle n} señores y r{displaystyle r} progenie per sire, podemos calcular la siguiente ANOVA, utilizando Vg{displaystyle V_{g} como la varianza genética y Ve{displaystyle V_{e} como la diferencia ambiental:
| Fuente | d.f. | Mean Square | Esperado Mean Square |
|---|---|---|---|
| Entre grupos de sire | n− − 1{displaystyle n-1} | S{displaystyle S. | 34Vg+Ve+r()14Vg){displaystyle {frac {3}{4}V_{g}+V_{e}+r({frac {f} {f} {fn}} {f}}}fn}fn} {1}{4}V_{g}}} |
| Dentro de grupos de sire | n()r− − 1){displaystyle n(r-1)} | W{displaystyle W. | 34Vg+Ve{displaystyle {frac {3}{4}V_{g}+V_{e} |
El 14Vg{displaystyle {frac}{4}V_{g} término es la correlación intraclase entre medias sibs. Podemos calcular fácilmente H2=VgVg+Ve=4()S− − W)S+()r− − 1)W{displaystyle H^{2}={frac {fnK} {fnMicroc {4(S-W)} {S+(r-1)W}}}}. El cuadrado medio esperado se calcula a partir de la relación de los individuos (progenía dentro de un sire son todos semi-sibs, por ejemplo), y una comprensión de las correlaciones intraclase.
El uso de ANOVA para calcular la heredabilidad a menudo no tiene en cuenta la presencia de interacciones gen-ambiente, porque ANOVA tiene un poder estadístico mucho menor para probar los efectos de interacción que los efectos directos.
Modelo con términos aditivos y de dominancia
Para un modelo con términos aditivos y de dominancia, pero no otros, la ecuación para un solo lugar geométrico es
- Sí.ij=μ μ +α α i+α α j+dij+e,{displaystyle Y... +alfa ¿Por qué? ¿Qué?
dónde
α α i{displaystyle alpha _{i} es el efecto aditivo del iT Allele, α α j{displaystyle alpha _{j}} es el efecto aditivo del jT Allele, dij{displaystyle d_{ij}} es la desviación dominante para el ijT genotipo, y e{displaystyle e} es el medio ambiente.
Los experimentos se pueden ejecutar con una configuración similar a la que se da en la tabla 1. Utilizando diferentes grupos de relaciones, podemos evaluar diferentes correlaciones intraclase. Uso Va{displaystyle V_{a} como la varianza genética aditiva y Vd{displaystyle V_{d} como la diferencia de desviación de dominio, las correlaciones intraclase se convierten en funciones lineales de estos parámetros. En general,
- Correlación intraclase=rVa+Silencio Silencio Vd,{displaystyle =rV_{a}+theta V_{d},}
Donde r{displaystyle r} y Silencio Silencio {displaystyle theta } se encuentran
r={displaystyle r=}P[ los alelos dibujados al azar del par de relación son idénticos por descenso], y
Silencio Silencio ={displaystyle theta =}P[ genotipos dibujados al azar del par de relación son idénticos por descenso].
Algunas relaciones comunes y sus coeficientes se dan en la Tabla 2.
| Relación | r{displaystyle r} | Silencio Silencio {displaystyle theta } |
|---|---|---|
| Gemelos idénticos | 1{displaystyle 1} | 1{displaystyle 1} |
| Parent-Offspring | 12{fnMicroc} {1}{2}}} | 0{displaystyle 0} |
| Medios hermanos | 14{fnMicroc} {1}{4}} | 0{displaystyle 0} |
| Full Siblings | 12{fnMicroc} {1}{2}}} | 14{fnMicroc} {1}{4}} |
| Primeros primos | 18{fnMicroc} {1}{8}} | 0{displaystyle 0} |
| Los primeros primos dobles | 14{fnMicroc} {1}{4}} | 116{displaystyle {frac {1}{16}} {fnK}}}} {fnK}}} {f}}}} {f}}} {f}}}}}} |
Modelos mixtos lineales
En la literatura se ha informado de una amplia variedad de enfoques que utilizan modelos mixtos lineales. A través de estos métodos, la variación fenotípica se divide en variaciones genéticas, ambientales y de diseño experimental para estimar la heredabilidad. La variación ambiental se puede modelar explícitamente mediante el estudio de individuos en una amplia gama de entornos, aunque la inferencia de la variación genética a partir de la variación fenotípica y ambiental puede llevar a subestimar la heredabilidad debido al desafío de capturar la gama completa de influencia ambiental que afecta un rasgo. Otros métodos para calcular la heredabilidad utilizan datos de estudios de asociación de todo el genoma para estimar la influencia de los factores genéticos en un rasgo, lo que se refleja en la tasa y la influencia de loci genéticos supuestamente asociados (generalmente polimorfismos de un solo nucleótido) en el rasgo. Sin embargo, esto puede llevar a subestimar la heredabilidad. Esta discrepancia se conoce como "falta de heredabilidad" y refleja el desafío de modelar con precisión la variación genética y ambiental en los modelos de heredabilidad.
Cuando se dispone de un pedigrí grande y complejo u otro tipo de datos mencionado anteriormente, la heredabilidad y otros parámetros genéticos cuantitativos se pueden estimar mediante la máxima verosimilitud restringida (REML) o métodos bayesianos. Los datos sin procesar generalmente tendrán tres o más puntos de datos para cada individuo: un código para el padre, un código para la madre y uno o varios valores de rasgos. Valores de características diferentes pueden ser para características diferentes o para puntos de medición diferentes en el tiempo.
La metodología actualmente popular se basa en altos grados de certeza sobre las identidades del padre y la madre; no es común tratar la identidad del padre de forma probabilística. Esto no suele ser un problema, ya que la metodología rara vez se aplica a poblaciones silvestres (aunque se ha utilizado para varias poblaciones de aves y ungulados silvestres), y los sementales se conocen invariablemente con un alto grado de certeza en los programas de reproducción. También hay algoritmos que dan cuenta de la paternidad incierta.
Los árboles genealógicos pueden verse con programas como Pedigree Viewer [1] y analizarse con programas como ASReml, VCE [2], WOMBAT [3], MCMCglmm dentro del entorno R [4] o la familia de programas BLUPF90 [5].
Los modelos genealógicos son útiles para desenredar factores de confusión como la causalidad inversa, los efectos maternos como el entorno prenatal y la confusión de la dominancia genética, el entorno compartido y los efectos de los genes maternos.
Heredabilidad genómica
Cuando se dispone de datos de genotipos y fenotipos de todo el genoma de grandes muestras de población, se pueden estimar las relaciones entre los individuos en función de sus genotipos y utilizar un modelo mixto lineal para estimar la varianza explicada por los marcadores genéticos. Esto proporciona una estimación de la heredabilidad genómica basada en la varianza capturada por las variantes genéticas comunes. Existen múltiples métodos que realizan diferentes ajustes para la frecuencia alélica y el desequilibrio de ligamiento. En particular, el método llamado High-Definition Likelihood (HDL) puede estimar la heredabilidad genómica utilizando solo estadísticas de resumen de GWAS, lo que facilita la incorporación de muestras de gran tamaño disponibles en varios metanálisis de GWAS.
Respuesta a la selección
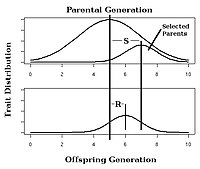
En la cría selectiva de plantas y animales, la respuesta esperada a la selección de un rasgo con heritabilidad de sentido estrecho conocido ()h2){displaystyle (h^{2})} se puede calcular utilizando el ecuación del criador:
- R=h2S{displaystyle R=h^{2}S}
En esta ecuación, la respuesta a la selección (R) se define como la diferencia promedio observada entre la generación principal y la siguiente, y el diferencial de selección (S) se define como la diferencia promedio entre la generación principal y la seleccionada. padres.
Por ejemplo, imagine que un fitomejorador está involucrado en un proyecto de reproducción selectiva con el objetivo de aumentar la cantidad de granos por mazorca de maíz. En aras del argumento, supongamos que la mazorca de maíz promedio en la generación de los padres tiene 100 granos. Supongamos también que los padres seleccionados producen maíz con un promedio de 120 granos por mazorca. Si h2 es igual a 0,5, la próxima generación producirá maíz con un promedio de 0,5(120-100) = 10 granos adicionales por mazorca. Por lo tanto, el número total de granos por mazorca de maíz será, en promedio, 110.
La observación de la respuesta a la selección en un experimento de selección artificial permitirá el cálculo de la heredabilidad realizada como en la figura 4.
Note que la heritabilidad en la ecuación anterior es igual a la relación Var()A)/Var()P){displaystyle mathrm {Var} (A)/mathrm {Var} (P)} sólo si el genotipo y el ruido ambiental siguen las distribuciones gausianas.
Controversias
Estimaciones de heredabilidad' críticos destacados, como Steven Rose, Jay Joseph y Richard Bentall, se centran en gran medida en las estimaciones de heredabilidad en las ciencias del comportamiento y las ciencias sociales. Bentall ha afirmado que tales puntajes de heredabilidad generalmente se calculan de manera contraria a la intuición para obtener puntajes numéricamente altos, que la heredabilidad se malinterpreta como determinación genética y que este supuesto sesgo distrae la atención de otros factores que las investigaciones han encontrado más causalmente importantes, como el abuso infantil que causa psicosis posterior. Las estimaciones de heredabilidad también son inherentemente limitadas porque no transmiten ninguna información sobre si los genes o el medio ambiente juegan un papel más importante en el desarrollo del rasgo en estudio. Por esta razón, David Moore y David Shenk describen el término "heredabilidad" en el contexto de la genética del comportamiento como "...uno de los más engañosos en la historia de la ciencia" y argumentan que no tiene valor excepto en casos muy raros. Cuando se estudian rasgos humanos complejos, es imposible utilizar el análisis de heredabilidad para determinar las contribuciones relativas de los genes y el medio ambiente, ya que dichos rasgos resultan de la interacción de múltiples causas. En particular, Feldman y Lewontin enfatizan que la heredabilidad es en sí misma una función de la variación ambiental. Sin embargo, algunos investigadores argumentan que es posible separar los dos.
La controversia sobre las estimaciones de heredabilidad se debe en gran parte a su base en estudios de gemelos. El escaso éxito de los estudios de genética molecular para corroborar tales estudios de genética de poblaciones' conclusiones es el problema de heredabilidad faltante. Eric Turkheimer ha argumentado que los métodos moleculares más nuevos han reivindicado la interpretación convencional de los estudios de gemelos, aunque sigue sin estar claro cómo explicar las relaciones entre los genes y los comportamientos. Según Turkheimer, tanto los genes como el entorno son hereditarios, la contribución genética varía según el entorno y centrarse en la heredabilidad distrae la atención de otros factores importantes. En general, sin embargo, la heredabilidad es un concepto ampliamente aplicable.
Contenido relacionado
Seno renal
Criobiología
Número triangular