Helio-4 superfluido

El helio-4 superfluido es la forma superfluida del helio-4, un isótopo del elemento helio. Un superfluido es un estado de la materia en el que la materia se comporta como un fluido con viscosidad cero. La sustancia, que parece un líquido normal, fluye sin fricción por cualquier superficie, lo que le permite seguir circulando sobre las obstrucciones y por los poros de los recipientes que la contienen, sujeta únicamente a su propia inercia.

Se sabe que la formación del superfluido está relacionada con la formación de un condensado de Bose-Einstein. Esto se hace evidente por el hecho de que la superfluidez se produce en el helio-4 líquido a temperaturas mucho más altas que en el helio-3. Cada átomo de helio-4 es una partícula de bosón, en virtud de su espín cero. El helio-3, sin embargo, es una partícula de fermión, que puede formar bosones solo apareándose consigo mismo a temperaturas mucho más bajas, en un proceso similar al apareamiento de electrones en la superconductividad.

Historia

Conocido como una faceta importante en el estudio de la hidrodinámica cuántica y los fenómenos cuánticos macroscópicos, Pyotr Kapitsa, John F. Allen y Don Misener descubrieron el efecto de superfluidez en 1937. Desde entonces, se ha descrito mediante teorías fenomenológicas y microscópicas.

En la década de 1950, Hall y Vinen realizaron experimentos para establecer la existencia de líneas de vórtice cuantificadas en helio superfluido. En la década de 1960, Rayfield y Reif establecieron la existencia de anillos de vórtice cuantizados. Packard ha observado la intersección de las líneas de vórtice con la superficie libre del fluido, y Avenel y Varoquaux han estudiado el efecto Josephson en helio-4 superfluido. En 2006, un grupo de la Universidad de Maryland visualizó vórtices cuantificados mediante el uso de pequeñas partículas trazadoras de hidrógeno sólido.

A principios de la década de 2000, los físicos crearon un condensado fermiónico a partir de pares de átomos fermiónicos ultrafríos. Bajo ciertas condiciones, los pares de fermiones forman moléculas diatómicas y sufren condensación de Bose-Einstein. En el otro límite, los fermiones (sobre todo los electrones superconductores) forman pares de Cooper que también presentan superfluidez. Este trabajo con gases atómicos ultrafríos ha permitido a los científicos estudiar la región entre estos dos extremos, conocida como cruce BEC-BCS.

Los supersólidos también pueden haber sido descubiertos en 2004 por físicos de la Universidad Estatal de Pensilvania. Cuando el helio-4 se enfría por debajo de unos 200 mK a altas presiones, una fracción (≈1 %) del sólido parece volverse superfluida. Mediante el enfriamiento rápido o el alargamiento del tiempo de recocido, aumentando o disminuyendo así la densidad del defecto respectivamente, se demostró, a través del experimento del oscilador torsional, que la fracción supersólida podía oscilar entre el 20 % y la inexistencia total. Esto sugirió que la naturaleza supersólida del helio-4 no es intrínseca al helio-4 sino una propiedad del helio-4 y el desorden. Algunas teorías emergentes postulan que la señal supersólida observada en el helio-4 era en realidad una observación de un estado de supervidrio o de límites de grano intrínsecamente superfluidos en el cristal de helio-4.

Aplicaciones

Recientemente, en el campo de la química, el helio-4 superfluido se ha utilizado con éxito en técnicas espectroscópicas como solvente cuántico. Denominada espectroscopia de gotas de helio superfluido (SHedS), es de gran interés en los estudios de moléculas de gas, ya que una sola molécula solvatada en un medio superfluido permite que una molécula tenga libertad de rotación efectiva, lo que le permite comportarse de manera similar a como lo haría en el "gasolina" fase. Las gotas de helio superfluido también tienen una temperatura característica de alrededor de 0,4 K que enfría la(s) molécula(s) solvatada(s) hasta su estado rovibrónico molido o casi molido.

Los superfluidos también se utilizan en dispositivos de alta precisión, como los giroscopios, que permiten medir algunos efectos gravitacionales predichos teóricamente (para ver un ejemplo, consulte Sonda de gravedad B).

El satélite astronómico infrarrojo IRAS, lanzado en enero de 1983 para recopilar datos infrarrojos, se enfrió con 73 kilogramos de helio superfluido, manteniendo una temperatura de 1,6 K (−271,55 °C). Cuando se usa junto con helio-3, se alcanzan habitualmente temperaturas tan bajas como 40 mK en experimentos con temperaturas extremadamente bajas. El helio-3, en estado líquido a 3,2 K, se puede evaporar en el superfluido helio-4, donde actúa como gas debido a las propiedades de este último como condensado de Bose-Einstein. Esta evaporación extrae energía del sistema general, que se puede bombear de una manera completamente análoga a las técnicas de refrigeración normales.

La tecnología de helio superfluido se utiliza para extender el rango de temperatura de los refrigeradores criogénicos a temperaturas más bajas. Hasta ahora, el límite es de 1,19 K, pero existe la posibilidad de llegar a 0,7 K.

Propiedades

Los superfluidos, como el helio-4 por debajo del punto lambda, exhiben muchas propiedades inusuales. Un superfluido actúa como si fuera una mezcla de un componente normal, con todas las propiedades de un fluido normal, y un componente superfluido. El componente superfluido tiene cero viscosidad y cero entropía. La aplicación de calor a un punto en helio superfluido da como resultado un flujo del componente normal que se encarga del transporte de calor a una velocidad relativamente alta (hasta 20 cm/s), lo que conduce a una conductividad térmica efectiva muy alta.

Flujo de película

Muchos líquidos ordinarios, como el alcohol o el petróleo, trepan por paredes sólidas, impulsados por su tensión superficial. El helio líquido también tiene esta propiedad, pero, en el caso del He-II, el flujo del líquido en la capa no está restringido por su viscosidad sino por una velocidad crítica que es de unos 20 cm/s. Esta es una velocidad bastante alta, por lo que el helio superfluido puede fluir con relativa facilidad hacia arriba por la pared de los contenedores, sobre la parte superior y hacia abajo hasta el mismo nivel que la superficie del líquido dentro del contenedor, en un efecto de sifón. Sin embargo, se observó que el flujo a través de la membrana nanoporosa se restringe si el diámetro del poro es inferior a 0,7 nm (es decir, aproximadamente tres veces el diámetro clásico del átomo de helio), lo que sugiere que las propiedades hidrodinámicas inusuales del He surgen a mayor escala que en el clásico helio líquido.

Rotación

Otra propiedad fundamental se hace visible si se coloca un superfluido en un recipiente giratorio. En lugar de rotar uniformemente con el contenedor, el estado de rotación consiste en vórtices cuantificados. Es decir, cuando el recipiente gira a velocidades por debajo de la primera velocidad angular crítica, el líquido permanece perfectamente estacionario. Una vez que se alcanza la primera velocidad angular crítica, el superfluido formará un vórtice. La fuerza del vórtice está cuantificada, es decir, un superfluido solo puede girar a ciertas velocidades "permitidas" valores. La rotación en un fluido normal, como el agua, no está cuantificada. Si se aumenta la velocidad de rotación, se formarán más y más vórtices cuantizados que se organizan en bonitos patrones similares a la red de Abrikosov en un superconductor.

Comparación con helio-3

Aunque las fenomenologías de los estados superfluidos del helio-4 y el helio-3 son muy similares, los detalles microscópicos de las transiciones son muy diferentes. Los átomos de helio-4 son bosones y su superfluidez se puede entender en términos de las estadísticas de Bose-Einstein que obedecen. Específicamente, la superfluidez del helio-4 puede considerarse como una consecuencia de la condensación de Bose-Einstein en un sistema interactivo. Por otro lado, los átomos de helio-3 son fermiones, y la transición superfluida en este sistema se describe mediante una generalización de la teoría de la superconductividad BCS. En él, el emparejamiento de Cooper tiene lugar entre átomos en lugar de electrones, y la interacción atractiva entre ellos está mediada por fluctuaciones de espín en lugar de fonones. (Ver condensado de fermión). Es posible una descripción unificada de la superconductividad y la superfluidez en términos de ruptura de la simetría de calibre.

Teoría macroscópica

Termodinámica

Fig. 1. Diagrama de fase ⁴Él. En este diagrama también se da la línea λ.

Fig. 2. Capacidad de calor del líquido ⁴Él a presión saturada de vapor como función de la temperatura. El pico en T=2.17 K marca una transición de fase (segundo pedido).

Fig. 3. La dependencia de la temperatura del superfluido relativo y componentes normales ρ_n/ y ρρ_s/ como funciones de T.

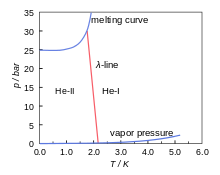
La figura 1 es el diagrama de fase de ⁴He. Es un diagrama de presión-temperatura (p-T) que indica las regiones sólida y líquida separadas por la curva de fusión (entre el estado líquido y sólido) y la región líquida y gaseosa, separadas por la línea de presión de vapor. Este último termina en el punto crítico donde desaparece la diferencia entre gas y líquido. El diagrama muestra la notable propiedad de que ⁴He es líquido incluso en el cero absoluto. ⁴Solo es sólido a presiones superiores a 25 bar.

La figura 1 también muestra la línea λ. Esta es la línea que separa dos regiones fluidas en el diagrama de fase indicado por He-I y He-II. En la región He-I el helio se comporta como un fluido normal; en la región He-II, el helio es superfluido.

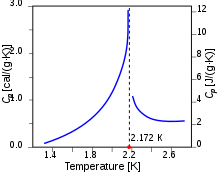
El nombre línea lambda proviene del gráfico de calor específico – temperatura que tiene la forma de la letra griega λ. Véase la figura 2, que muestra un pico a 2,172 K, el llamado punto λ de ⁴He.

Por debajo de la línea lambda, el líquido se puede describir mediante el llamado modelo de dos fluidos. Se comporta como si constara de dos componentes: un componente normal, que se comporta como un fluido normal, y un componente superfluido con viscosidad cero y entropía cero. Las relaciones de las respectivas densidades ρ_n/ρ y ρ_s/ρ, con ρ_n (ρ_s) la densidad del componente normal (superfluido), y ρ (la densidad total), depende de la temperatura y se representa en la figura 3. Al bajar la temperatura, la fracción de la densidad del superfluido aumenta desde cero en T_λ a uno en cero kelvins. Por debajo de 1 K, el helio es casi completamente superfluido.

Es posible crear ondas de densidad del componente normal (y por lo tanto del componente superfluido ya que ρ_n + ρ_s = constante) que son similares al sonido ordinario ondas. Este efecto se llama segundo sonido. Debido a la dependencia de la temperatura de ρ_n (figura 3), estas ondas en ρ_n también son ondas de temperatura.

Fig. 4. El helio II "creep" a lo largo de las superficies para encontrar su propio nivel – después de un corto tiempo, los niveles en los dos contenedores se igualarán. La película Rollin también cubre el interior del contenedor más grande; si no estuviera sellada, el helio II se arrastraría y escaparía.

Fig. 5. El helio líquido está en la fase superfluida. Mientras permanezca superfluo, se arrastra por la pared de la copa como una película delgada. Se baja en el exterior, formando una gota que caerá en el líquido debajo. Otra gota formará – y así sucesivamente – hasta que la taza esté vacía.

Hidrodinámica de superfluidos

La ecuación de movimiento del componente superfluido, en una forma algo simplificada, viene dada por la ley de Newton

F→ → =M4dv→ → sdt.{displaystyle {vec}=M_{4}{frac {mathrm {d} {fnMicrosoft Sans Serif}

La masa M₄ es la masa molar ⁴Él y v→ → s{displaystyle {vec {}_{s}} es la velocidad del componente superfluido. El derivado del tiempo es el denominado derivado hidrodinámico, es decir, la tasa de aumento de la velocidad al moverse con el fluido. En el caso de superfluida ⁴Él en el campo gravitacional la fuerza es dada por

F→ → =− − Silencio Silencio → → ()μ μ +M4gz).{displaystyle {vec {vec}=-{vec {nabla} {mu +M_{4}gz).}

En esta expresión, μ es el potencial químico molar, g la aceleración gravitatoria y z la coordenada vertical. Así obtenemos la ecuación que establece que la termodinámica de una cierta constante será amplificada por la fuerza de la aceleración gravitatoria natural

M4dv→ → sdt=− − Silencio Silencio → → ()μ μ +M4gz).{displaystyle M_{4}{frac} {mhm} {fnK} {fnK} {fnK}=-{vec {nabla} {mu +M_{4}gz).}

()1)

Ec. (1) solo se cumple si v_s está por debajo de cierto valor crítico, que generalmente está determinado por el diámetro del canal de flujo.

En la mecánica clásica, la fuerza suele ser el gradiente de una energía potencial. ecuación (1) muestra que, en el caso del componente superfluido, la fuerza contiene un término debido al gradiente del potencial químico. Este es el origen de las notables propiedades del He-II, como el efecto fuente.

Fig. 6. Vía de integración para calcular μ en arbitrarios p y T.

Fig. 7. Demostración de la presión de la fuente. Los dos vasos están conectados por un superleak a través del cual sólo el componente superfluido puede pasar.

Fig. 8. Demostración del efecto fuente. Un tubo capilar es "cerrado" en un extremo por un superleak y se coloca en un baño de helio superfluido y luego calentado. El helio fluye hacia arriba a través del tubo y pica como una fuente.

Presión de la fuente

Para reescribir la Ec.(1) en una forma más familiar usamos la fórmula general

dμ μ =Vmdp− − SmdT.{displaystyle mathrm {d} mu =V_{m}mathrm T.

()2)

Aquí S_m es la entropía molar y V_m el volumen molar. Con la Ec.(2) μ(p,T) se puede encontrar mediante una integración lineal en el plano p-T. Primero integramos desde el origen (0,0) a (p,0), entonces en T =0. Luego integramos desde (p,0) a (p,T), así que con presión constante (ver figura 6). En la primera integral dT=0 y en la segunda dp=0. Con la Ec.(2) obtenemos

μ μ ()p,T)=μ μ ()0,0)+∫ ∫ 0pVm()p.. ,0)dp.. − − ∫ ∫ 0TSm()p,T.. )dT.. .{displaystyle mu (p,T)=mu (0,0)+int ¿Qué? ¿Qué? T^{prime }

()3)

Solo nos interesan los casos en los que p es pequeño, de modo que V_m es prácticamente constante. Asi que

∫ ∫ 0pVm()p.. ,0)dp.. =Vm0p{displaystyle int ¿Qué? }=V_{m0}p}

()4)

donde V_m0 es el volumen molar del líquido en T =0 y p =0. El otro término en la Ec.(3) también se escribe como un producto de V_m0 y una cantidad p _f que tiene la dimensión de presión

∫ ∫ 0TSm()p,T.. )dT.. =Vm0pf.{displaystyle int ¿Qué? T^{prime }=V_{m0}p_{f}

()5)

La presión p_f se llama presión de la fuente. Se puede calcular a partir de la entropía de ⁴He que, a su vez, se puede calcular a partir de la capacidad calorífica. Para T =T_λ la presión de la fuente es igual a 0,692 bar. Con una densidad de helio líquido de 125 kg/m³ y g = 9,8 m/s² esto corresponde a una columna de helio líquido de 56 metros de altura. Entonces, en muchos experimentos, la presión de la fuente tiene un efecto mayor en el movimiento del helio superfluido que la gravedad.

Con las Ecs.(4) y (5), la Ec.(3) obtiene la forma

μ μ ()p,T)=μ μ 0+Vm0()p− − pf).{displaystyle mu (p,T)=mu _{0}+V_{m0}(p-p_{f}).}

()6)

La sustitución de la Ec.(6) en (1) da

*** *** 0dv→ → sdt=− − Silencio Silencio → → ()p+*** *** 0gz− − pf).{displaystyle rho _{0}{frac {mathrm {d} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}(p+rho _{0}gz-p_{f}}}

()7)

con ρ₀ = M₄/V_m0 la densidad de líquido ⁴He a presión y temperatura cero.

Eq.(7) muestra que el componente superfluido es acelerado por gradientes en la presión y en el campo gravitatorio, como de costumbre, pero también por un gradiente en la fuente de presión.

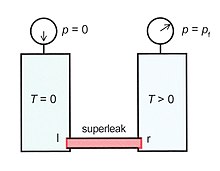
Hasta ahora, la Ec.(5) solo tiene significado matemático, pero en arreglos experimentales especiales p_f puede aparecer como una presión real. La Figura 7 muestra dos recipientes que contienen He-II. Se supone que el recipiente izquierdo está a cero kelvins (T_l=0) y cero presión (p_l = 0). Los vasos están conectados por una llamada superfuga. Este es un tubo lleno de un polvo muy fino, por lo que se bloquea el flujo del componente normal. Sin embargo, el componente superfluido puede fluir a través de esta superfuga sin ningún problema (por debajo de una velocidad crítica de unos 20 cm/s). En el estado estacionario v_s=0 entonces Eq.(7) implica

pl+*** *** 0gzl− − pfl=pr+*** *** 0gzr− − pfr{displaystyle P_{l}+rho ¿Por qué? ¿Qué?

()8)

donde el índice l (r) se aplica al lado izquierdo (derecho) de la superfuga. En este caso particular p_l = 0, z_l = z_r, y p_fl = 0 (ya que T_l = 0). Como consecuencia,

0=pr− − pfr.{displaystyle 0=p_{r}-p_{fr}

Esto significa que la presión en el recipiente derecho es igual a la presión de la fuente en T_r.

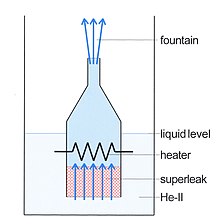
En un experimento, dispuesto como en la figura 8, se puede crear una fuente. El efecto fuente se utiliza para impulsar la circulación de ³He en refrigeradores de dilución.

Fig. 9. Transporte de calor por un contraflujo de los componentes normales y superfluos de He-II

Transporte de calor

La Figura 9 muestra un experimento de conducción de calor entre dos temperaturas T_H y T_L conectadas por un tubo lleno de He-II. Cuando se aplica calor al extremo caliente, se acumula presión en el extremo caliente de acuerdo con la Ec.(7). Esta presión impulsa el componente normal desde el extremo caliente al extremo frío de acuerdo con

Δ Δ p=− − .. nZVÍ Í n.{displaystyle Delta p=-eta # Z{n}Z{dot {V}_{n}.}

()9)

Aquí._n es la viscosidad del componente normal, Z algún factor geométrico, y VÍ Í n{displaystyle { dot {fn} el flujo de volumen. El flujo normal está equilibrado por un flujo del componente superfluido del frío al extremo caliente. En las secciones finales se realiza una conversión normal a superfluida y viceversa. Así que el calor es transportado, no por conducción de calor, sino por convección. Este tipo de transporte de calor es muy eficaz, por lo que la conductividad térmica de He-II es mucho mejor que los mejores materiales. La situación es comparable con las tuberías de calor donde el calor se transporta a través de la conversión de gas líquido. La alta conductividad térmica de He-II se aplica para estabilizar imanes superconductores como en el Gran Colisionador de Hadrones en CERN.

Teoría microscópica

Enfoque de dos fluidos de Landau

L. La teoría fenomenológica y semimicroscópica de la superfluidez del helio-4 de D. Landau le valió el Premio Nobel de física en 1962. Suponiendo que las ondas sonoras son las excitaciones más importantes en el helio-4 a bajas temperaturas, demostró que el helio-4 que fluye más allá de una pared no crearía excitaciones espontáneamente si la velocidad del flujo fuera menor que la velocidad del sonido. En este modelo, la velocidad del sonido es la "velocidad crítica" por encima del cual se destruye la superfluidez. (El helio-4 en realidad tiene una velocidad de flujo más baja que la velocidad del sonido, pero este modelo es útil para ilustrar el concepto). Landau también demostró que la onda de sonido y otras excitaciones podrían equilibrarse entre sí y fluir por separado del resto del helio. -4, que se conoce como "condensado".

A partir del impulso y la velocidad de flujo de las excitaciones, pudo definir un "fluido normal" densidad, que es cero a temperatura cero y aumenta con la temperatura. A la llamada temperatura Lambda, donde la densidad normal del fluido es igual a la densidad total, el helio-4 ya no es superfluido.

Para explicar los primeros datos de calor específico del helio-4 superfluido, Landau postuló la existencia de un tipo de excitación que denominó "rotón", pero a medida que disponía de mejores datos, consideró que el ";rotón" era lo mismo que una versión de sonido de alto impulso.

La teoría de Landau no elabora la estructura microscópica del componente superfluido del helio líquido. Los primeros intentos de crear una teoría microscópica del propio componente superfluido fueron realizados por London y, posteriormente, por Tisza. Otros modelos microscópicos han sido propuestos por diferentes autores. Su principal objetivo es derivar la forma del potencial entre partículas entre átomos de helio en estado superfluido a partir de los primeros principios de la mecánica cuántica. Hasta la fecha, se han propuesto varios modelos de este tipo, incluidos: modelos con anillos de vórtice, modelos de esfera dura y teorías de cúmulos gaussianos.

Modelo de anillo de vórtice

Landau pensó que la vorticidad entraba en el helio-4 superfluido a través de láminas de vórtice, pero desde entonces se ha demostrado que dichas láminas son inestables. Lars Onsager y, posteriormente, de forma independiente, Feynman demostraron que la vorticidad entra por líneas de vórtice cuantizadas. También desarrollaron la idea de los anillos de vórtice cuánticos. Arie Bijl en la década de 1940, y Richard Feynman alrededor de 1955, desarrollaron teorías microscópicas para el roton, que Palevsky observó en breve con experimentos de neutrones inelásticos. Más tarde, Feynman admitió que su modelo solo da concordancia cualitativa con el experimento.

Modelos de esfera dura

Los modelos se basan en la forma simplificada del potencial entre partículas entre los átomos de helio-4 en la fase superfluida. Es decir, se supone que el potencial es del tipo de esfera dura. En estos modelos se reproduce cualitativamente el famoso espectro de excitaciones de Landau (roton).

Enfoque de clúster gaussiano

Este es un enfoque de dos escalas que describe el componente superfluido del helio-4 líquido. Eso consta de dos modelos anidados vinculados a través del espacio paramétrico. La parte de longitud de onda corta describe la estructura interior del elemento fluido utilizando un enfoque no perturbativo basado en la ecuación logarítmica de Schrödinger; sugiere el comportamiento de tipo gaussiano de la densidad interior del elemento y el potencial de interacción entre partículas. La parte de longitud de onda larga es la teoría cuántica de muchos cuerpos de tales elementos que se ocupa de su dinámica e interacciones. El enfoque proporciona una descripción unificada de las excitaciones de fonones, maxones y rotones, y tiene un acuerdo notable con el experimento: con un parámetro esencial para ajustar, se reproduce con alta precisión el espectro de rotones de Landau, la velocidad del sonido y el factor de estructura del helio-4 superfluido. Este modelo utiliza la teoría general de los líquidos cuánticos de Bose con no linealidades logarítmicas que se basa en la introducción de una contribución de tipo disipativo a la energía relacionada con la función de entropía cuántica de Everett-Hirschman.