Hashing extensible

El hash extensible es un tipo de sistema hash que trata un hash como una cadena de bits y utiliza un trie para la búsqueda en el contenedor. Debido a la naturaleza jerárquica del sistema, el rehashing es una operación incremental (se realiza un contenedor a la vez, según sea necesario). Esto significa que las aplicaciones sensibles al tiempo se ven menos afectadas por el crecimiento de la tabla que por los rehashes estándar de tabla completa.

El hash extensible fue descrito por Ronald Fagin en 1979. Prácticamente todos los sistemas de archivos modernos utilizan hash extensible o árboles B. En particular, el sistema de archivos global, ZFS y el sistema de archivos SpadFS utilizan hash extensible.

Supongamos que la función hash ${\displaystyle h(k)}$ devuelve una cuerda de bits. La primera ${\displaystyle i}$ bits de cada cadena se utilizarán como índices para averiguar a dónde irán en el "directorio" ( tabla de barras), donde ${\displaystyle i}$ es el número más pequeño tal que el índice de cada elemento en la tabla es único.

Teclas a utilizar:

${\displaystyle {\begin{aligned}h(k_{1})=100100\h(k_{2})=0110\h(k_{3})=110\end{aligned}}$

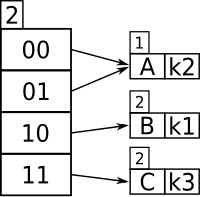
Supongamos que, para este ejemplo en particular, el tamaño del depósito es 1. Las dos primeras claves que se insertarán, k₁ y k₂, se pueden distinguir por el bit más significativo y se insertarían en la tabla de la siguiente manera:

Ahora bien, si se tuviera que aplicar un algoritmo hash a k₃ en la tabla, no sería suficiente distinguir las tres claves por un bit (porque tanto k₃ como k₁ tienen 1 como su bit más a la izquierda). Además, como el tamaño del contenedor es uno, la tabla se desbordaría. Como comparar los dos primeros bits más significativos daría a cada clave una ubicación única, el tamaño del directorio se duplica de la siguiente manera:

Y ahora k₁ y k₃ tienen una ubicación única, y se distinguen por los dos primeros bits más a la izquierda. Como k₂ está en la mitad superior de la tabla, tanto 00 como 01 apuntan a él porque no hay otra clave con la que comparar que comience con un 0.

El ejemplo anterior es de Fagin et al. (1979).

${\displaystyle h(k_{4}=011110}$

Ahora, es necesario insertar k₄, y tiene los dos primeros bits como 01..(1110), y utilizando una profundidad de 2 bits en el directorio, esto asigna de 01 al Bucket A. El Bucket A está lleno (tamaño máximo 1), por lo que debe dividirse; debido a que hay más de un puntero al Bucket A, no hay necesidad de aumentar el tamaño del directorio.

Lo que se necesita es información sobre:

1. El tamaño clave que mapea el directorio (la profundidad global), y
2. El tamaño clave que previamente ha mapeado el cubo (la profundidad local)

Para distinguir los dos casos de acción:

1. Duplicar el directorio cuando un cubo se llena
2. Crear un cubo nuevo, y re-distribuir las entradas entre el viejo y el nuevo cubo

Si examinamos el caso inicial de una estructura hash extensible, si cada entrada de directorio apunta a un contenedor, entonces la profundidad local debería ser igual a la profundidad global.

La cantidad de entradas de directorio es igual a 2^{profundidad global}, y la cantidad inicial de contenedores es igual a 2^{profundidad local}.

Por lo tanto, si la profundidad global = profundidad local = 0, entonces 2⁰ = 1, es decir, un directorio inicial de un puntero a un contenedor.

Volvamos a los dos casos de acción; si el cubo está lleno:

1. Si la profundidad local es igual a la profundidad global, entonces sólo hay un puntero al cubo, y no hay otros punteros del directorio que pueden mapear al cubo, por lo que el directorio debe ser duplicado.
2. Si la profundidad local es menor que la profundidad global, entonces existe más de un puntero desde el directorio hasta el cubo, y el cubo se puede dividir.

La clave 01 apunta al contenedor A, y la profundidad local del contenedor A de 1 es menor que la profundidad global del directorio de 2, lo que significa que las claves cifradas al contenedor A solo han utilizado un prefijo de 1 bit (es decir, 0), y el contenedor necesita dividir su contenido utilizando claves de 1 + 1 = 2 bits de longitud; en general, para cualquier profundidad local d donde d es menor que D, la profundidad global, entonces d debe incrementarse después de una división del contenedor, y el nuevo d debe utilizarse como el número de bits de la clave de cada entrada para redistribuir las entradas del contenedor anterior en los nuevos contenedores.

Ahora,

${\displaystyle h(k_{4}=011110}$

es probado de nuevo, con 2 bits 01., y ahora clave 01 puntos a un nuevo cubo pero todavía ⁠${\displaystyle K_{2}$⁠ en él (${\displaystyle h(k_{2}=010110}$ y también comienza con 01).

Si ⁠${\displaystyle K_{2}$⁠ había sido 000110, con la llave 00, no habría habido ningún problema, porque ⁠${\displaystyle K_{2}$⁠ habría permanecido en el nuevo cubo A' y el cubo D habría estado vacío.

(Este habría sido el caso más probable con diferencia cuando los contenedores son de un tamaño mayor que 1 y sería extremadamente improbable que los contenedores recién divididos se desbordaran, a menos que todas las entradas se volvieran a dividir en un solo contenedor. Pero solo para enfatizar el papel de la información de profundidad, el ejemplo se seguirá de manera lógica hasta el final).

Por lo tanto, es necesario dividir el contenedor D, pero la comprobación de su profundidad local, que es 2, es la misma que la profundidad global, que es 2, por lo que el directorio debe dividirse nuevamente para contener claves con suficiente detalle, por ejemplo, 3 bits.

1. El cubo D necesita dividirse debido a estar lleno.
2. Como la profundidad local de D = la profundidad global, el directorio debe duplicarse para aumentar el poco detalle de las teclas.
3. La profundidad global ha aumentado después de la división del directorio a 3.
4. La nueva entrada ⁠${\displaystyle K_{4}$⁠ se vuelve con profundidad global 3 bits y termina en D que tiene profundidad local 2, que ahora puede ser incrementado a 3 y D se pueden dividir a D' y E.
5. El contenido del cubo de división D, ⁠${\displaystyle K_{2}$⁠, ha sido revestido con 3 bits, y termina en D'.
6. K4 es retriado y termina en E que tiene una ranura de repuesto.

Ahora, ${\displaystyle h(k_{2}=010110}$ está en D y ${\displaystyle h(k_{4}=011110}$ es probado de nuevo, con 3 bits 011.., y señala a cubo D que ya contiene ⁠${\displaystyle K_{2}$⁠ así que está lleno; la profundidad local de D es 2 pero ahora la profundidad global es 3 después de la duplicación del directorio, por lo que ahora D puede dividirse en D' y E del balde, el contenido de D, ⁠${\displaystyle K_{2}$⁠ tiene ${\displaystyle h(k_{2}}$ retrito con un nuevo bitmask de profundidad global de 3 y ⁠${\displaystyle K_{2}$⁠ termina en D', luego la nueva entrada ⁠${\displaystyle K_{4}$⁠ se retira con ${\displaystyle h(k_{4}}$ bitmasked utilizando el nuevo recuento global de profundidad de 3 y esto da 011 que ahora apunta a un nuevo cubo E que está vacío. Así que... ⁠${\displaystyle K_{4}$⁠ va a Bucket E.

A continuación se muestra el algoritmo de hash extensible en Python, con la asociación de bloques de disco/páginas de memoria, el almacenamiento en caché y los problemas de consistencia eliminados. Tenga en cuenta que existe un problema si la profundidad excede el tamaño de bits de un entero, porque entonces la duplicación del directorio o la división de un contenedor no permitirá que las entradas se vuelvan a codificar en contenedores diferentes.

El código utiliza los bits menos significativos, lo que hace que sea más eficiente expandir la tabla, ya que todo el directorio se puede copiar como un bloque (Ramakrishnan y Gehrke (2003)).

PAGE_SZ = 10clase Página: def __init_()auto) - No. Ninguno: auto.mapa = [] auto.local_fund = 0 def completo()auto) - No. bool: Regreso Len()auto.mapa) >= PAGE_SZ def #()auto, k, v) - No. Ninguno: para i, ()clave, valor) dentro enumerado()auto.mapa): si clave == k: del auto.mapa[i] descanso auto.mapa.apéndice(()k, v) def #()auto, k): para clave, valor dentro auto.mapa: si clave == k: Regreso valor def get_local_high_bit()auto): Regreso 1 c) c) auto.local_fundclase ExtendibleHashing: def __init_()auto) - No. Ninguno: auto.global_fund = 0 auto.directorio = [Página()] def get_page()auto, k): h = hash()k) Regreso auto.directorio[h " (()1 c) c) auto.global_fund) - 1) def #()auto, k, v) - No. Ninguno: p = auto.get_page()k) completo = p.completo() p.#()k, v) si completo: si p.local_fund == auto.global_fund: auto.directorio *= 2 auto.global_fund += 1 p0 = Página() p1 = Página() p0.local_fund = p1.local_fund = p.local_fund + 1 high_bit = p.get_local_high_bit() para k2, v2 dentro p.mapa: h = hash()k2) new_p = p1 si h " high_bit más p0 new_p.#()k2, v2) para i dentro rango()hash()k) " ()high_bit - 1), Len()auto.directorio), high_bit): auto.directorio[i] = p1 si i " high_bit más p0 def #()auto, k): Regreso auto.get_page()k).#()k)si __name_ == "__main__": ¿Eh? = ExtendibleHashing() N = 10088 l = lista()rango()N) importación al azar al azar.shuffle()l) para x dentro l: ¿Eh?.#()x, x) impresión()l) para i dentro rango()N): impresión()¿Eh?.#()i)

• Trie
• Hash table
• Stable hashing
• Castigo persistente
• Hacha lineal

• Fagin, R.; Nievergelt, J.; Pippenger, N.; Strong, H. R. (septiembre de 1979), "Extendible Hashing - Un método de acceso rápido para archivos dinámicos", Transacciones ACM sobre sistemas de bases de datos, 4 (3): 315–344, doi:10.1145/320083.320092, S2CID 2723596
• Ramakrishnan, R.; Gehrke, J. (2003), Sistemas de gestión de bases de datos, 3a edición: Capítulo 11, Índice de base de hash, págs. 373 a 378
• Silberschatz, Abraham; Korth, Henry; Sudarshan, S., Conceptos del sistema de bases de datos, Sexta edición: Capítulo 11.7, Hashing dinámico

• Este artículo incorpora material de dominio público Paul E. Black. "Escandaloso". Diccionario de Algoritmos y Estructuras de Datos. NIST.
• Notas extensibles de Hashing en la Universidad Estatal de Arkansas
• Notas de corte extensibles Archived 2016-03-03 en la máquina Wayback
• Slides from the database System Concepts book on extendible hashing for hash based dynamic indices