Habló
Un radio es una de varias varillas que irradian desde el centro de una rueda (el cubo donde se conecta el eje), conectando el cubo con la superficie de tracción redonda.
El término se refería originalmente a las partes de un tronco que se habían partido (partido a lo largo) en cuatro o seis secciones. Los miembros radiales de una rueda de carreta se hicieron tallando un radio (de un tronco) en su forma final. Un Spokeshave es una herramienta desarrollada originalmente para este propósito. Eventualmente, el término radio se aplicó más comúnmente al producto terminado del trabajo del carpintero que a los materiales que usaban.
Historia
La rueda de radios se inventó para permitir la construcción de vehículos más ligeros y rápidos. La evidencia física más antigua de ruedas con radios se encontró en la cultura Sintashta, que data de c. 2000 a. Poco después de esto, las culturas ecuestres de la región del Cáucaso utilizaron carros de guerra con ruedas de radios tirados por caballos durante la mayor parte de los tres siglos. Se adentraron en la península griega donde se unieron a los pueblos mediterráneos existentes para dar lugar, finalmente, a la Grecia clásica después de la ruptura del dominio minoico y las consolidaciones lideradas por la Esparta y Atenas preclásicas.
Las pinturas del período neocalcolítico/protohistórico (1800-1200 a. C.) en varias regiones de la India, como Chibbar Nulla, Chhatur Bhoj Nath Nulla, Kathotia, etc., representan el uso de carros con ruedas de radios.
Los carros celtas introdujeron un borde de hierro alrededor de la rueda en el primer milenio a. La rueda de radios se siguió utilizando sin modificaciones importantes hasta la década de 1870, cuando se inventaron las ruedas de alambre y los neumáticos de goma.
Construcción
Los radios pueden ser de madera, metal o fibra sintética dependiendo de si estarán en tensión o compresión.
Radios de compresión
El tipo original de rueda de radios con radios de madera se usaba para carruajes y carros tirados por caballos. En los primeros automóviles, normalmente se usaban ruedas de radios de madera del tipo de artillería.
En una rueda de madera simple, una carga en el cubo hace que el borde de la rueda se aplaste ligeramente contra el suelo a medida que el radio de madera más bajo se acorta y comprime. Los otros radios de madera no muestran cambios significativos.
Los radios de madera se montan radialmente. También están abombados, generalmente hacia el exterior del vehículo, para evitar que se tambalee. Además, el abombamiento permite que la rueda compense la expansión de los radios debido a la humedad absorbida al abombarse más.
Radios de tensión
Para su uso en bicicletas, las ruedas pesadas con radios de madera fueron reemplazadas por ruedas más livianas con radios hechos de alambres de metal ajustables y tensados, llamados ruedas de alambre. Estos también se utilizan en sillas de ruedas, motocicletas, automóviles y los primeros aviones.
Tipos
Algunos tipos de ruedas tienen radios extraíbles que se pueden reemplazar individualmente si se rompen o doblan. Estos incluyen ruedas de bicicletas y sillas de ruedas. Las bicicletas de alta calidad con ruedas convencionales usan radios de acero inoxidable, mientras que las bicicletas más económicas pueden usar radios galvanizados (también llamados "sin óxido") o cromados. Mientras que un radio de buena calidad es capaz de soportar alrededor de 225 kgf (c. 500 libras-fuerza o 2200 newtons) de tensión, se utilizan con una fracción de esta carga para evitar sufrir fallas por fatiga. Dado que los radios de las ruedas de bicicletas y sillas de ruedas solo están en tensión, ocasionalmente también se utilizan materiales flexibles y resistentes, como las fibras sintéticas. Los radios de metal también se pueden ovalar o aplanar para reducir la resistencia aerodinámica y empalmar (el doble o incluso el triple) para reducir el peso y mantener la resistencia.
Una variación de la rueda de radios de alambre fue el "Disco de tensión" de Tioga, que superficialmente parecía ser un disco sólido, pero de hecho se construyó utilizando los mismos principios que una rueda de radios de tensión normal. rueda. En lugar de radios de alambre individuales, se utilizó un hilo continuo de Kevlar (aramida) para unir el buje a la llanta bajo alta tensión. Los hilos estaban encerrados en un disco translúcido para protección y algún beneficio aerodinámico, pero esto no era un componente estructural.
| medidor de alambre | diámetro | Sección |
|---|---|---|
| 15G | 1.8 mm | 3.24 mm2 |
| 14G | 2.0 mm | 4 mm2 |
| 13G | 2.3 mm | 5.29 mm2 |
| 12G | 2.6 mm | 6,76 mm2 |
| 11G | 2.9 mm | 8.41 mm2 |
| 10G | 3.2 mm | 10.24 mm2 |
Cordón tangencial
Los radios de alambre pueden ser radiales al cubo, pero con más frecuencia se montan tangencialmente al cubo. Los radios tangenciales permiten la transferencia de par entre la llanta y el buje. Por lo tanto, los radios tangenciales son necesarios para la rueda motriz, que tiene torque en el cubo debido al pedaleo, y cualquier rueda que use frenos montados en el cubo, como frenos de disco o de banda, que transfieren el torque desde la llanta al freno en la dirección opuesta (a través de buje) al frenar.
Construcción de ruedas
La construcción de una rueda con radios tensados a partir de sus partes constituyentes se denomina construcción de ruedas y requiere el procedimiento de construcción correcto para obtener un producto final resistente y duradero. Los radios tensados generalmente se unen a la llanta o, a veces, al buje con una boquilla de radio. El otro extremo comúnmente se martilla en un disco o rara vez se dobla en forma de "Z" para evitar que tire a través de su agujero en el cubo. La versión doblada tiene la ventaja de reemplazar un radio roto en una rueda trasera de bicicleta sin tener que quitar los engranajes traseros.
Las llantas de alambre, con su excelente relación peso-resistencia, pronto se hicieron populares para los vehículos livianos. Para los autos de todos los días, las ruedas de alambre pronto fueron reemplazadas por ruedas de disco de metal menos costosas, pero las ruedas de alambre siguieron siendo populares para los autos deportivos hasta la década de 1960. Las ruedas con radios siguen siendo populares en motocicletas y bicicletas.
Longitud de radios
Al construir una rueda de bicicleta, los radios deben tener la longitud correcta; de lo contrario, es posible que no haya suficientes hilos enganchados, lo que produce una rueda más débil, o pueden sobresalir a través de la llanta y posiblemente perforar la cámara de aire.
Cálculo
Para los radios de bicicleta, la longitud del radio se define desde el asiento de la brida hasta la punta de la rosca. Para radios con extremos doblados, la longitud nominal del radio no incluye el ancho del radio en el extremo doblado.
Para ruedas con radios cruzados (que son la norma), la longitud de radio deseada es
- l=d2+r12+r22− − 2r1r2# ()a)− − r3{displaystyle l={sqrt {2} {2}} {2} {2}} {2}} {2}}} {2},r_{1}r_{2}cos(a)}}-r_{3}
dónde
- d = distancia del centro del eje (a lo largo del eje) a la brida, por ejemplo 30 mm,
- r1 = radio de círculo de agujeros en el cubo, por ejemplo 19,5 mm,
- r2 = la mitad del Diámetro Rim efectivo (ERD), o el diámetro de los extremos de los radios hacen en una rueda construida (ver 'Discusión' adjunta a este artículo para explicación) del borde, por ejemplo 301 mm,
- r3 = radio de agujeros en el radio brida, por ejemplo 1.1 mm,
- m = número de radios a utilizar para un lado de la rueda, por ejemplo 36/2=18,
- k = número de cruces por radio, por ejemplo 3 y
- a = 360° k/m, por ejemplo 360°*3/18 = 60°.
Con respecto a d: Para una rueda simétrica como una rueda delantera sin freno de disco, esta es la mitad de la distancia entre las pestañas. Para una rueda asimétrica como una rueda delantera con freno de disco o una rueda trasera con cambio de cadena, el valor de d es diferente para los lados izquierdo y derecho.
a es el ángulo entre (1) el radio hasta el orificio de la boquilla en la llanta a la que se une un radio y (2) el radio hasta el Orificio de la brida que sujeta el radio. El radio cruza 1, 2 o 3 radios que apuntan de manera opuesta, según el diseño de los cordones. En la brida, el ángulo entre los radios de los agujeros adyacentes es de 360°/m (para agujeros igualmente espaciados). Para cada radio cruzado, el buje se gira con referencia al "ángulo de la llanta entre los orificios de las bridas adyacentes". Por lo tanto, al multiplicar el "ángulo entre orificios de brida adyacentes" por k da el ángulo a. Por ejemplo, una rueda de 32 radios tiene 16 radios por lado, 360° dividido por 16 es igual a 22,5°. Multiplique 22,5° ("ángulo entre orificios de brida adyacentes") por el número de cruces para obtener el ángulo a: si hay 3 cruces, los 32 radios rueda tiene un ángulo a de 67,5°. Respecto a r3: El tamaño de los agujeros de los radios en la brida no importa para la longitud de radios necesaria. Este término elimina el efecto del tamaño del agujero. Dado que los agujeros suelen ser pequeños (poco más de 2 mm de diámetro), el efecto es pequeño y en la práctica importa poco.
Para ruedas con radios radiales (pasos por cero), la fórmula se simplifica al teorema de Pitágoras, con una longitud de radio l más r 3 siendo la pendiente, r2 menos r1 siendo la base, y d siendo la elevación:
- ()l+r3)2=()r2− − r1)2+d2{displaystyle (l+r_{3})^{2}=(r_{2}-r_{1}^{2}+d^{2}}; o resolución para la longitud
- l=d2+()r2− − r1)2− − r3.{displaystyle l={2}-r_{3}.}
Derivación
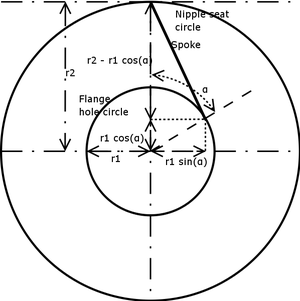
La fórmula de la longitud de los radios calcula la longitud de la diagonal del espacio de una caja rectangular imaginaria. Imagínese sosteniendo una rueda frente a usted de tal manera que un pezón esté en la parte superior. Mira la rueda desde el eje. El rayo a través del orificio superior ahora es una diagonal de la caja imaginaria. La caja tiene una profundidad de d, una altura de r2-r1cos(α) y un ancho de r1sin(a).
De manera equivalente, la ley de los cosenos se puede usar para calcular primero la longitud del radio tal como se proyecta en el plano de la rueda (como se ilustra en el diagrama), seguido de una aplicación del teorema de Pitágoras.
Contenido relacionado
Guerra de información
Ferrocarril de Caledonia (Brechin)
Aceite (desambiguación)