Guía de ondas
Una guía de ondas es una estructura que guía las ondas, como las ondas electromagnéticas o el sonido, con una pérdida mínima de energía al restringir la transmisión de energía a una dirección. Sin la restricción física de una guía de ondas, las intensidades de las ondas disminuyen según la ley del inverso del cuadrado a medida que se expanden en el espacio tridimensional.
Existen diferentes tipos de guías de ondas para diferentes tipos de ondas. El significado original y más común es un tubo de metal conductor hueco que se usa para transportar ondas de radio de alta frecuencia, particularmente microondas. Las guías de ondas dieléctricas se utilizan en frecuencias de radio más altas, y las guías de ondas dieléctricas transparentes y las fibras ópticas sirven como guías de ondas para la luz. En acústica, los conductos de aire y las bocinas se utilizan como guías de onda para el sonido en instrumentos musicales y altavoces, y las varillas de metal de forma especial conducen ondas ultrasónicas en el mecanizado ultrasónico.
La geometría de una guía de ondas refleja su función; Además de los tipos más comunes que canalizan la onda en una dimensión, existen guías de ondas de losa bidimensionales que limitan las ondas a dos dimensiones. La frecuencia de la onda transmitida también dicta el tamaño de una guía de ondas: cada guía de ondas tiene una longitud de onda de corte determinada por su tamaño y no conducirá ondas de mayor longitud de onda; una fibra óptica que guía la luz no transmitirá microondas que tienen una longitud de onda mucho mayor. Algunas estructuras naturales también pueden actuar como guías de ondas. La capa del canal SOFAR en el océano puede guiar el sonido del canto de las ballenas a través de enormes distancias. Cualquier forma de sección transversal de la guía de ondas puede admitir ondas EM. Las formas irregulares son difíciles de analizar. Las guías de ondas comúnmente utilizadas tienen forma rectangular y circular.
Usos
Los usos de las guías de ondas para transmitir señales se conocían incluso antes de que se acuñara el término. El fenómeno de las ondas de sonido guiadas a través de un cable tenso se conoce desde hace mucho tiempo, así como el sonido a través de un tubo hueco como una cueva o un estetoscopio médico. Otros usos de las guías de ondas son la transmisión de energía entre los componentes de un sistema, como la radio, el radar o los dispositivos ópticos. Las guías de ondas son el principio fundamental de las pruebas de ondas guiadas (GWT), uno de los muchos métodos de evaluación no destructiva.
Ejemplos específicos:
- Las fibras ópticas transmiten luz y señales para largas distancias con baja atenuación y una amplia gama utilizable de longitudes de onda.
- En un horno de microondas una guía de onda transfiere el poder del magnetrón, donde se forman ondas, a la cámara de cocción.
- En un radar, una guía de onda transfiere energía de radio frecuencia a y desde la antena, donde la impedancia debe ser igualada para una transmisión eficiente de energía (ver abajo).
- Las guías de onda rectangulares y circulares se utilizan comúnmente para conectar los alimentos de los platos parabólicos a su electrónica, ya sea receptores de ruido bajo o amplificador de potencia/transmisores.
- Las ondas se utilizan en instrumentos científicos para medir propiedades ópticas, acústicas y elásticas de materiales y objetos. La guía de onda se puede poner en contacto con el espécimen (como en una ultrasonografía médica), en cuyo caso la guía de onda asegura que el poder de la onda de prueba se conserva, o el espécimen puede ser puesto dentro de la guía de onda (como en una medición constante dieléctrica), para que los objetos más pequeños puedan ser probados y la precisión es mejor.
- Una línea de transmisión es un tipo de guía de onda comúnmente utilizado.
Historia
La primera estructura para guiar ondas fue propuesta por J. J. Thomson en 1893, y Oliver Lodge la probó experimentalmente por primera vez en 1894. Lord Rayleigh realizó el primer análisis matemático de ondas electromagnéticas en un cilindro de metal en 1897. Para las ondas de sonido, Lord Rayleigh publicó un análisis matemático completo de los modos de propagación en su obra fundamental, "La teoría del sonido". Jagadish Chandra Bose investigó longitudes de onda milimétricas utilizando guías de ondas, y en 1897 describió a la Royal Institution de Londres su investigación realizada en Kolkata.
El estudio de las guías de ondas dieléctricas (como las fibras ópticas, ver más abajo) comenzó en la década de 1920, por varias personas, las más famosas de las cuales son Rayleigh, Sommerfeld y Debye. La fibra óptica comenzó a recibir atención especial en la década de 1960 debido a su importancia para la industria de las comunicaciones.
El desarrollo de la comunicación por radio se produjo inicialmente en las frecuencias más bajas porque podían propagarse más fácilmente a grandes distancias. Las largas longitudes de onda hicieron que estas frecuencias no fueran adecuadas para su uso en guías de ondas de metal hueco debido a que se requerían tubos de gran diámetro poco prácticos. En consecuencia, la investigación sobre guías de ondas de metal hueco se estancó y el trabajo de Lord Rayleigh fue olvidado por un tiempo y tuvo que ser redescubierto por otros. Las investigaciones prácticas se reanudaron en la década de 1930 por George C. Southworth en Bell Labs y Wilmer L. Barrow en MIT. Southworth al principio tomó la teoría de artículos sobre ondas en varillas dieléctricas porque desconocía el trabajo de Lord Rayleigh. Esto lo engañó un poco; algunos de sus experimentos fallaron porque no era consciente del fenómeno de la frecuencia de corte de la guía de ondas que ya se encuentra en el trabajo de Lord Rayleigh. John R. Carson y Sallie P. Mead asumieron un trabajo teórico serio. Este trabajo condujo al descubrimiento de que para el modo TE01 en la guía de ondas circular, las pérdidas disminuyen con la frecuencia y en un momento esto fue un serio competidor para el formato de las telecomunicaciones de larga distancia.
La importancia del radar en la Segunda Guerra Mundial dio un gran impulso a la investigación de la guía de ondas, al menos en el lado aliado. El magnetrón, desarrollado en 1940 por John Randall y Harry Boot en la Universidad de Birmingham en el Reino Unido, proporcionó una buena fuente de energía e hizo viable el radar de microondas. El centro de investigación más importante de los EE. UU. estaba en el Laboratorio de Radiación (Rad Lab) del MIT, pero muchos otros participaron en los EE. UU. y en el Reino Unido, como el Establecimiento de Investigación de Telecomunicaciones. El jefe del Grupo de Desarrollo Fundamental en Rad Lab fue Edward Mills Purcell. Sus investigadores incluyeron a Julian Schwinger, Nathan Marcuvitz, Carol Gray Montgomery y Robert H. Dicke. Gran parte del trabajo de Rad Lab se concentró en encontrar modelos de elementos agrupados de estructuras de guía de ondas para que los componentes en la guía de ondas pudieran analizarse con la teoría de circuitos estándar. Hans Bethe también estuvo brevemente en Rad Lab, pero mientras estuvo allí produjo su teoría de apertura pequeña que resultó importante para los filtros de cavidad de guía de onda, desarrollados por primera vez en Rad Lab. El lado alemán, por otro lado, ignoró en gran medida el potencial de las guías de ondas en el radar hasta muy avanzada la guerra. Tanto es así que cuando se enviaron piezas de radar de un avión británico derribado a Siemens & Halske para el análisis, a pesar de que fueron reconocidos como componentes de microondas, no se pudo identificar su propósito.
En ese momento, las técnicas de microondas eran muy descuidadas en Alemania. Se creía generalmente que no era de utilidad para la guerra electrónica, y no se permitía a quienes querían hacer trabajos de investigación en este campo.
—H. Mayer, vicepresidente de guerra de Siemens " Halske
A académicos alemanes incluso se les permitió continuar publicando sus investigaciones en este campo porque no se consideraba importante.
Inmediatamente después de la Segunda Guerra Mundial, la guía de ondas fue la tecnología preferida en el campo de las microondas. Sin embargo, tiene algunos problemas; es voluminoso, costoso de producir y el efecto de la frecuencia de corte dificulta la producción de dispositivos de banda ancha. La guía de onda estriada puede aumentar el ancho de banda más allá de una octava, pero una mejor solución es utilizar una tecnología que funcione en modo TEM (es decir, sin guía de onda), como los conductores coaxiales, ya que TEM no tiene una frecuencia de corte. También se puede utilizar un conductor rectangular apantallado y esto tiene ciertas ventajas de fabricación sobre el coaxial y puede verse como el precursor de las tecnologías planas (stripline y microstrip). Sin embargo, las tecnologías planas realmente comenzaron a despegar cuando se introdujeron los circuitos impresos. Estos métodos son significativamente más baratos que la guía de ondas y han ocupado en gran medida su lugar en la mayoría de las bandas. Sin embargo, la guía de ondas todavía se prefiere en las bandas de microondas más altas desde alrededor de la banda Ku hacia arriba.
Propiedades
Modos de propagación y frecuencias de corte
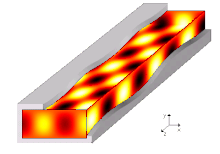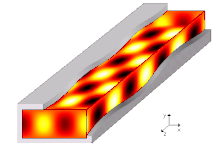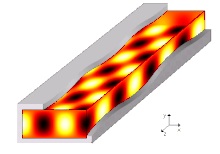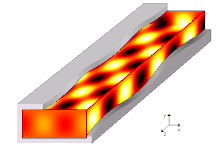
Un modo de propagación en una guía de onda es una solución de las ecuaciones de onda o, en otras palabras, la forma de la onda. Debido a las restricciones de las condiciones de contorno, solo hay frecuencias y formas limitadas para la función de onda que pueden propagarse en la guía de ondas. La frecuencia más baja en la que un determinado modo puede propagarse es la frecuencia de corte de ese modo. El modo con la frecuencia de corte más baja es el modo fundamental de la guía de ondas, y su frecuencia de corte es la frecuencia de corte de la guía de ondas.
Los modos de propagación se computan resolviendo la ecuación de Helmholtz junto con un conjunto de condiciones de límite dependiendo de la forma geométrica y los materiales que atan la región. La suposición habitual de las guías uniformes infinitamente largas nos permite asumir una forma propagadora para la onda, es decir, afirmando que cada componente de campo tiene una dependencia conocida de la dirección de propagación (es decir,. z{displaystyle z}). Más concretamente, el enfoque común consiste en sustituir primero todos los campos desconocidos que van por el tiempo u()x,Sí.,z,t){displaystyle u(x,y,z,t)} (suponiendo la simplicidad para describir los campos en componentes cartesianos) con su compleja representación de faasores U()x,Sí.,z){displaystyle U(x,y,z)}, suficiente para describir completamente cualquier señal de una sola tono infinitamente larga a frecuencia f{displaystyle f}, (frecuencia triangular ⋅ ⋅ =2π π f{displaystyle omega =2pi f}), y reescribir la ecuación de Helmholtz y las condiciones de límites en consecuencia. Entonces, cada campo desconocido se ve obligado a tener una forma como U()x,Sí.,z)=U^ ^ ()x,Sí.)e− − γ γ z{displaystyle U(x,y,z)={hat {U}(x,y)e^{-gamma z}, donde el γ γ {displaystyle gamma } término representa la constante de propagación (todavía desconocida) a lo largo de la dirección que la guía de onda se extiende al infinito. La ecuación de Helmholtz puede ser reescrita para dar cabida a tal forma y la igualdad resultante debe ser resuelta para γ γ {displaystyle gamma } y U^ ^ ()x,Sí.){displaystyle {hat {U}(x,y)}, produciendo al final una ecuación de valor eigenvalo para γ γ {displaystyle gamma } y una función eigen correspondiente U^ ^ ()x,Sí.)γ γ {displaystyle {hat {U}(x,y)_{gamma }para cada solución del primero.
La constante de propagación γ γ {displaystyle gamma } de la onda guiada es compleja, en general. Para un caso sin pérdidas, se puede encontrar la constante de propagación para asumir valores reales o imaginarios, dependiendo de la solución elegida de la ecuación de eigenvalue y de la frecuencia angular ⋅ ⋅ {displaystyle omega }. Cuando γ γ {displaystyle gamma } es puramente real, se dice que el modo es "below cutoff", ya que la amplitud de los fasores de campo tiende a disminuir exponencialmente con la propagación; un imaginario γ γ {displaystyle gamma }, en cambio, representa los modos que se dice que están "en propagación" o "arriba de amor", ya que la amplitud compleja de los faasores no cambia con z{displaystyle z}.
Coincidencia de impedancia
En la teoría del circuito, la impedancia es una generalización de la resistencia eléctrica en el caso de la corriente alterna, y se mide en ohms (Ω Ω {displaystyle Omega }). Una guía de onda en la teoría del circuito es descrita por una línea de transmisión que tiene una longitud y impedancia característica. En otras palabras, la impedancia indica la relación del voltaje a la corriente del componente del circuito (en este caso una guía de onda) durante la propagación de la onda. Esta descripción de la guía de onda fue originalmente diseñada para alternar la corriente, pero también es adecuada para ondas electromagnéticas y sonoras, una vez que las propiedades de onda y material (como presión, densidad, constante dieléctrica) se convierten adecuadamente en términos eléctricos (corriente e impedancia por ejemplo).
La coincidencia de impedancia es importante cuando se conectan los componentes de un circuito eléctrico (por ejemplo, la guía de ondas a la antena): la relación de impedancia determina la cantidad de onda que se transmite hacia adelante y la cantidad que se refleja. Al conectar una guía de ondas a una antena, generalmente se requiere una transmisión completa, por lo que se hace un esfuerzo para igualar sus impedancias.
El coeficiente de reflexión se puede calcular utilizando: .. =Z2− − Z1Z2+Z1{displaystyle Gamma ={frac {Z_{2}-Z_{1} {Z_{2}}, donde .. {displaystyle "Gamma" (Gamma) es el coeficiente de reflexión (0 denota transmisión completa, 1 reflexión completa, y 0.5 es un reflejo de la mitad del voltaje entrante), Z1{displaystyle Z_{1} y Z2{displaystyle Z_{2} son la impedancia del primer componente (de donde entra la onda) y el segundo componente, respectivamente.
Un desajuste de impedancia crea una onda reflejada, que se suma a las ondas entrantes crea una onda de pie. Un desajuste de impedancia también se puede cuantificar con la relación de onda de pie (SWR o VSWR para tensión), que se conecta a la relación de impedancia y coeficiente de reflexión por: VSWR=SilencioVSilenciomaxSilencioVSilenciomin=1+Silencio.. Silencio1− − Silencio.. Silencio{displaystyle mathrm {VSWR} ={frac Oh, Dios mío. { min}={frac} {1+ AnteriorGamma Silencio!, donde SilencioVSilenciomin/max{displaystyle left WordPressVright sometida_{rm {min/max}} son los valores mínimos y máximos del valor absoluto de voltaje, y el VSWR es la relación de onda de voltaje, que valor de 1 denota la transmisión completa, sin reflexión y por lo tanto sin onda de pie, mientras que valores muy grandes significan alta reflexión y patrón de onda de pie.
Guías de ondas electromagnéticas
Guías de ondas de radiofrecuencia
Las guías de ondas se pueden construir para transportar ondas en una amplia porción del espectro electromagnético, pero son especialmente útiles en los rangos de frecuencia óptica y de microondas. Dependiendo de la frecuencia, pueden construirse con materiales conductores o dieléctricos. Las guías de ondas se utilizan para transferir tanto energía como señales de comunicación.

Guías de ondas ópticas
Las guías de ondas utilizadas en frecuencias ópticas suelen ser guías de ondas dieléctricas, estructuras en las que un material dieléctrico con alta permitividad y, por lo tanto, alto índice de refracción, está rodeado por un material con menor permitividad. La estructura guía las ondas ópticas por reflexión interna total. Un ejemplo de guía de ondas ópticas es la fibra óptica,
También se utilizan otros tipos de guías de ondas ópticas, incluida la fibra de cristal fotónico, que guía las ondas mediante cualquiera de varios mecanismos distintos. Las guías en forma de tubo hueco con una superficie interior altamente reflectante también se han utilizado como conductos de luz para aplicaciones de iluminación. Las superficies internas pueden ser de metal pulido o pueden estar cubiertas con una película multicapa que guía la luz por reflexión de Bragg (este es un caso especial de una fibra de cristal fotónico). También se pueden usar pequeños prismas alrededor de la tubería que reflejan la luz a través de la reflexión interna total [1]; sin embargo, dicho confinamiento es necesariamente imperfecto, ya que la reflexión interna total nunca puede guiar realmente la luz dentro de un núcleo de índice más bajo. (en la caja del prisma, algo de luz se filtra por las esquinas del prisma).
Guías de ondas acústicas
Una guía de ondas acústicas es una estructura física para guiar las ondas sonoras. El sonido en una guía de onda acústica se comporta como ondas electromagnéticas en una línea de transmisión. Las ondas en una cuerda, como las de un teléfono de lata, son un ejemplo simple de una guía de ondas acústica. Otro ejemplo son las ondas de presión en los tubos de un órgano. El término guía de ondas acústicas también se utiliza para describir ondas elásticas guiadas en dispositivos de microescala, como los empleados en las líneas de retardo piezoeléctricas y en la dispersión de Brillouin estimulada.
Guías de ondas matemáticas
Las guías de ondas son interesantes objetos de estudio desde una perspectiva estrictamente matemática. Una guía de ondas (o tubo) se define como un tipo de condición límite en la ecuación de onda tal que la función de onda debe ser igual a cero en el límite y que la región permitida es finita en todas las dimensiones menos una (un cilindro infinitamente largo es un ejemplo.) A partir de estas condiciones generales se puede demostrar un gran número de resultados interesantes. Resulta que cualquier tubo con una protuberancia (donde aumenta el ancho del tubo) admite al menos un estado límite que existe dentro de los espacios de modo. Las frecuencias de todos los estados ligados se pueden identificar usando un pulso corto en el tiempo. Esto se puede demostrar usando los principios variacionales. Un resultado interesante de Jeffrey Goldstone y Robert Jaffe es que cualquier tubo de ancho constante con una torsión admite un estado ligado.
Síntesis de sonido
La síntesis de sonido utiliza líneas de retardo digitales como elementos computacionales para simular la propagación de ondas en los tubos de los instrumentos de viento y las cuerdas vibrantes de los instrumentos de cuerda.
Contenido relacionado
Yuri Gagarin
KA9Q
Transporte en Irak