Grupo dicíclico

En la teoría de grupos, un grupo dicíclico (notación Dic_n o Q_4n, ⟨n,2,2⟩) es un tipo particular de grupo no abeliano de orden 4n (n > 1). Es una extensión del grupo cíclico de orden 2 por un grupo cíclico de orden 2n, dando el nombre de dicíclico. En la notación de sucesiones exactas de grupos, esta extensión se puede expresar como:

1→ → C2n→ → Dicn→ → C2→ → 1.{displaystyle 1to C_{2n}to {mbox{Dic}_{n}to C_{2}to 1.,}

Más generalmente, dado cualquier grupo abeliano finito con un elemento de orden 2, se puede definir un grupo dicíclico.

Definición

Para cada entero n > 1, el grupo dicíclico Dic_n se puede definir como el subgrupo de los cuaterniones unitarios generados por

a=eiπ π n=#⁡ ⁡ π π n+ipecado⁡ ⁡ π π nx=j{displaystyle {begin{aligned}a ventaja=e^{frac} {fnMicrosoft Sans Serif} } {n}=cos {frac {fn} ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################

De manera más abstracta, se puede definir el grupo dicíclico Dic_n como el grupo con la siguiente presentación

Dicn=.a,x▪ ▪ a2n=1,x2=an,x− − 1ax=a− − 1..{displaystyle operatorname {Dic} _{n}=leftlangle a,xmid a^{2n}=1, x^{2}=a^{n}, x^{-1}ax=a^{-1}rightrangle.

Algunas cosas a tener en cuenta que se derivan de esta definición:

• x4=1{displaystyle x^{4}=1}
• x2ak=ak+n=akx2{displaystyle ¿Qué?
• si j=± ± 1{displaystyle j=pm 1}, entonces xjak=a− − kxj{displaystyle x^{j}a}=a^{-k}x^{j}
• akx− − 1=ak− − nanx− − 1=ak− − nx2x− − 1=ak− − nx{displaystyle a^{k}x^{-1}=a^{k-n}a^{n}x^{-1}=a^{k-n}x^{2}x^{-1}=a^{k-n}x}

Por lo tanto, cada elemento de Dic_n puede escribirse únicamente como a^kx^j, donde 0 ≤ k < 2n y j = 0 o 1. Las reglas de multiplicación están dadas por

• akam=ak+m{displaystyle a^{k}a}=a^{k+m}
• akamx=ak+mx{displaystyle a^{k}a^{m}x=a^{k+m}x}
• akxam=ak− − mx{displaystyle a^{k}xa^{m}=a^{k-m}x}
• akxamx=ak− − m+n{displaystyle a^{k}xa^{m}x=a^{k-m+n}

Se sigue que Dic_n tiene orden 4n.

Cuando n = 2, el grupo dicíclico es isomorfo al grupo cuaternión Q. Más generalmente, cuando n es una potencia de 2, el grupo dicíclico es isomorfo al grupo cuaternión generalizado.

Propiedades

Para cada n > 1, el grupo dicíclico Dic_n es un grupo no abeliano de orden 4n. (Para el caso degenerado n = 1, el grupo Dic₁ es el grupo cíclico C₄, que es no se considera dicíclico.)

Sea A = ⟨a⟩ el subgrupo de Dic_n generado por a. Entonces A es un grupo cíclico de orden 2n, entonces [Dic_n:A] = 2. Como subgrupo del índice 2 es automáticamente un subgrupo normal. El grupo cociente Dic_n/A es un grupo cíclico de orden 2.

Dic_n tiene solución; tenga en cuenta que A es normal y, al ser abeliano, es solucionable.

Grupo diedro binario

El grupo dicíclico es un grupo poliédrico binario — es una de las clases de subgrupos del grupo Pin Pin₋(2), que es un subgrupo del grupo Spin Spin(3) — y en este contexto se conoce como el grupo diédrico binario.

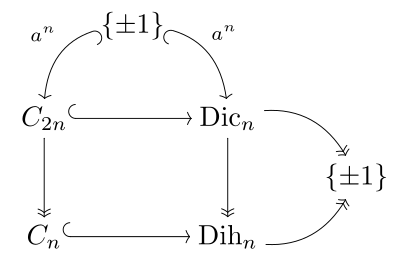
La conexión con el grupo cíclico binario C_2n, el grupo cíclico C_n, y el grupo diédrico Dih_n de orden 2n se ilustra en el diagrama de la derecha, y es paralelo al diagrama correspondiente para el grupo Pin. Coxeter escribe el grupo diédrico binario como ⟨2,2,n⟩ y grupo cíclico binario con paréntesis angulares, ⟨n⟩.

Existe un parecido superficial entre los grupos dicíclicos y los grupos diédricos; ambos son una especie de "espejo" de un grupo cíclico subyacente. Pero la presentación de un grupo diédrico tendría x² = 1, en lugar de x² = unⁿ; y esto produce una estructura diferente. En particular, Dic_n no es un producto semidirecto de A y ⟨x⟩, ya que A ∩ ⟨x⟩ no es trivial.

El grupo dicíclico tiene una involución única (es decir, un elemento de orden 2), a saber, x² = aⁿ. Tenga en cuenta que este elemento se encuentra en el centro de Dic_n. De hecho, el centro consta únicamente del elemento identidad y x². Si a la presentación de Dic_n le sumamos la relación x² = 1 se obtiene una presentación del diedro grupo Dih_n, por lo que el grupo cociente Dic_n/<x²> es isomorfo a Dih_n.

Hay un homomorfismo natural de 2 a 1 del grupo de cuaterniones unitarios al grupo de rotación tridimensional descrito en cuaterniones y rotaciones espaciales. Dado que el grupo dicíclico puede estar incrustado dentro de los cuaterniones unitarios, uno puede preguntarse cuál es su imagen bajo este homomorfismo. La respuesta es simplemente el grupo de simetría diédrica Dih_n. Por esta razón, el grupo dicíclico también se conoce como grupo diédrico binario. Tenga en cuenta que el grupo dicíclico no contiene ningún subgrupo isomorfo a Dih_n.

La construcción de imagen previa análoga, usando Pin₊(2) en lugar de Pin₋(2), produce otro grupo diédrico, Dih_2n, en lugar de un grupo dicíclico.

Generalizaciones

Sea A un grupo abeliano, teniendo un elemento específico y en A de orden 2. Un grupo G se llama un grupo dicíclico generalizado, escrito como Dic(A, y), si se genera por A y un elemento adicional x, y además tenemos que [G:A] = 2, x² = y, y para todo a en A, x⁻¹ax = a⁻¹.

Dado que para un grupo cíclico de orden par, siempre hay un único elemento de orden 2, podemos ver que los grupos dicíclicos son solo un tipo específico de grupo dicíclico generalizado.