Gramática libre de contexto

Ajustar Compartir Imprimir Citar

Tipo de gramática formal

Extracto simplificado de la gramática formal para el lenguaje de programación C (izquierda), y derivación de una pieza de código C (derecho) del símbolo no terminal

{displaystyle langle {text{Stmt}}rangle }

. Los símbolos no terminales y terminales se muestran en azul y rojo, respectivamente.

En la teoría del lenguaje formal, una gramática independiente del contexto (CFG) es una gramática formal cuyas reglas de producción son de la forma

A to alpha

con $A$ a single símbolo no final, y $alpha$ a string of terminals and/or nonterminals ( $alpha$ puede estar vacío). Una gramática formal es "libre de texto" si sus reglas de producción se pueden aplicar independientemente del contexto de un no-terminal. No importa qué símbolos lo rodean, el único noterminal en el lado izquierdo siempre puede ser reemplazado por el lado derecho. Esto lo distingue de una gramática sensible al contexto.

Una gramática formal es esencialmente un conjunto de reglas de producción que describen todas las cadenas posibles en un lenguaje formal dado. Las reglas de producción son reemplazos simples. Por ejemplo, la primera regla en la imagen,

{displaystyle langle {text{Stmt}}rangle to langle {text{Id}}rangle =langle {text{Expr}}rangle;}

reemplazantes ${displaystyle langle {text{Stmt}}rangle }$ con ${displaystyle langle {text{Id}}rangle =langle {text{Expr}}rangle;}$ . Puede haber múltiples reglas de reemplazo para un símbolo no final dado. El lenguaje generado por una gramática es el conjunto de todas las cadenas de símbolos terminales que se pueden derivar, mediante aplicaciones de regla repetidas, de algún símbolo no-terminal particular ("símbolo de inicio"). Los símbolos noterminales se utilizan durante el proceso de derivación, pero no aparecen en su cadena de resultado final.

Los lenguajes generados por gramáticas libres de contexto se conocen como lenguajes libres de contexto (CFL). Diferentes gramáticas libres de contexto pueden generar el mismo lenguaje libre de contexto. Es importante distinguir las propiedades del lenguaje (propiedades intrínsecas) de las propiedades de una gramática particular (propiedades extrínsecas). La cuestión de la igualdad lingüística (¿dos gramáticas libres de contexto dadas generan el mismo lenguaje?) es indecidible.

Las gramáticas libres de contexto surgen en lingüística donde se utilizan para describir la estructura de oraciones y palabras en un lenguaje natural, y fueron inventadas por el lingüista Noam Chomsky para este propósito. Por el contrario, en informática, a medida que aumentó el uso de conceptos definidos recursivamente, se utilizaron cada vez más. En una aplicación temprana, las gramáticas se utilizan para describir la estructura de los lenguajes de programación. En una aplicación más nueva, se utilizan en una parte esencial del Lenguaje de marcado extensible (XML) denominado Definición de tipo de documento.

En lingüística, algunos autores utilizan el término gramática de estructura sintagmática para referirse a las gramáticas independientes del contexto, en las que las gramáticas con estructura sintagmática son distintas de las gramáticas de dependencia. En informática, una notación popular para las gramáticas independientes del contexto es la forma de Backus-Naur, o BNF.

Antecedentes

Desde la época de Pāṇini, al menos, los lingüistas han descrito las gramáticas de los idiomas en términos de su estructura de bloques y han descrito cómo las oraciones se construyen recursivamente a partir de frases más pequeñas y, finalmente, palabras individuales o elementos de palabras. Una propiedad esencial de estas estructuras de bloques es que las unidades lógicas nunca se superponen. Por ejemplo, la oración:

John, cuyo coche azul estaba en el garaje, caminó hasta la tienda de comestibles.

puede estar lógicamente entre paréntesis (con los metasímbolos lógicos [ ]) de la siguiente manera:

[John.[, [cuyo [coche azul]] [era [dentro [el garaje]],]] [Caminar [a [el [tienda de comestibles]]].

Una gramática independiente del contexto proporciona un mecanismo simple y matemáticamente preciso para describir los métodos mediante los cuales se construyen frases en algún lenguaje natural a partir de bloques más pequeños, capturando la "estructura de bloque" de oraciones de forma natural. Su simplicidad hace que el formalismo sea susceptible de un estudio matemático riguroso. Las características importantes de la sintaxis del lenguaje natural, como la concordancia y la referencia, no forman parte de la gramática independiente del contexto, sino la estructura recursiva básica de las oraciones, la forma en que las cláusulas se anidan dentro de otras cláusulas y la forma en que se ordenan las listas de adjetivos y adverbios. tragado por sustantivos y verbos, se describe exactamente.

Las gramáticas libres de contexto son una forma especial de los sistemas Semi-Thue que, en su forma general, se remontan al trabajo de Axel Thue.

El formalismo de las gramáticas independientes del contexto fue desarrollado a mediados de la década de 1950 por Noam Chomsky, y también su clasificación como un tipo especial de gramática formal (a la que llamó gramáticas de estructura sintagmática). Algunos autores, sin embargo, reservan el término para gramáticas más restringidas en la jerarquía de Chomsky: gramáticas sensibles al contexto o gramáticas libres de contexto. En un sentido más amplio, las gramáticas de estructura sintagmática también se conocen como gramáticas de constituyentes. El rasgo definitorio de las gramáticas de estructura sintagmática es, por lo tanto, su adhesión a la relación de electorado, en oposición a la relación de dependencia de las gramáticas de dependencia. En el marco de la gramática generativa de Chomsky, la sintaxis del lenguaje natural se describía mediante reglas independientes del contexto combinadas con reglas de transformación.

La estructura de bloques fue introducida en los lenguajes de programación de computadoras por el proyecto Algol (1957–1960), que, como consecuencia, también presentó una gramática libre de contexto para describir la sintaxis de Algol resultante. Esto se convirtió en una característica estándar de los lenguajes informáticos, y la notación para las gramáticas utilizadas en las descripciones concretas de los lenguajes informáticos se conoció como forma Backus-Naur, en honor a dos miembros del comité de diseño del lenguaje Algol. La "estructura de bloques" El aspecto que capturan las gramáticas libres de contexto es tan fundamental para la gramática que los términos sintaxis y gramática a menudo se identifican con reglas gramaticales libres de contexto, especialmente en informática. Las restricciones formales no capturadas por la gramática se consideran entonces parte de la "semántica" del idioma

Las gramáticas libres de contexto son lo suficientemente simples como para permitir la construcción de algoritmos de análisis eficientes que, para una cadena determinada, determinan si se puede generar a partir de la gramática y cómo. Un analizador Earley es un ejemplo de dicho algoritmo, mientras que los analizadores LR y LL ampliamente utilizados son algoritmos más simples que se ocupan solo de subconjuntos más restrictivos de gramáticas libres de contexto.

Definiciones formales

Una gramática sin contexto $G$ se define por el 4-tuple $G=(V,SigmaR,S)$ , Donde

$V$ es un conjunto finito; cada elemento $vin V$ se llama a carácter no terminal o a variable. Cada variable representa un tipo diferente de frase o cláusula en la frase. Las variables también se llaman categorías sintácticas. Cada variable define un sub-idioma del lenguaje definido por $G$ .
$.$ es un conjunto finito de terminals, disjoint from $V$ , que componen el contenido real de la frase. El conjunto de terminales es el alfabeto del idioma definido por la gramática $G$ .
$R$ es una relación finita en ${displaystyle Vtimes (Vcup Sigma)^{*}}$ , donde el asterisco representa la operación estelar Kleene. Los miembros de $R$ son llamados (reescribir) reglao produccións de la gramática. (también comúnmente simbolizado por un $P$ )
$S$ es la variable de inicio (o símbolo de inicio), utilizada para representar toda la frase (o programa). Debe ser un elemento $V$ .

Notación de regla de producción

Una regla de producción $R$ es formalizado matemáticamente como un par $(alphabeta)in R$ , donde $alpha in V$ es un no-terminal y $beta in (Vcup Sigma)^{*}$ es una cadena de variables y/o terminales; en lugar de usar notación de par ordenada, las reglas de producción generalmente se escriben usando un operador de flecha con $alpha$ como su lado izquierdo y $β$ como su lado derecho: $alpha rightarrow beta$ .

Está permitido $β$ ser la cuerda vacía, y en este caso es costumbre denotarla por ε. La forma $alpha rightarrow varepsilon$ se llama $ε$ -producción.

Es común enumerar todos los lados de la mano derecha para el mismo lado izquierdo en la misma línea, utilizando TEN (la barra vertical) para separarlos. Reglas $alpha rightarrow beta _{1}$ y $alpha rightarrow beta _{2}$ puede ser escrito como $alpha rightarrow beta _{1}mid beta _{2}$ . En este caso, $beta _{1}$ y $beta _{2}$ se llaman la primera y segunda alternativa, respectivamente.

Aplicación de reglas

Para cualquier cadena $u,vin (Vcup Sigma)^{*}$ , decimos $u$ rendimientos directos $v$ , escrito como $uRightarrow v,$ , si $exists (alphabeta)in R$ con $alpha in V$ y $u_{1},u_{2}in (Vcup Sigma)^{*}$ tales que $u,=u_{1}alpha u_{2}$ y $v,=u_{1}beta u_{2}$ . Así, $v$ es el resultado de la aplicación de la regla $(alphabeta)$ a $u$ .

Aplicación de regla repetitiva

Para cualquier cadena $u,vin (Vcup Sigma)^{*},$ diremos $u$ rendimientos $v$ o $v$ es derivada desde $u$ si hay un entero positivo $k$ y cuerdas ${displaystyle u_{1},ldotsu_{k}in (Vcup Sigma)^{*}}$ tales que ${displaystyle u=u_{1}Rightarrow u_{2}Rightarrow cdots Rightarrow u_{k}=v}$ . Esta relación es denotada $u{stackrel {*}{Rightarrow }}v$ , o ${displaystyle uRightarrow Rightarrow v}$ en algunos libros de texto. Si $kgeq 2$ , la relación $u{stackrel {+}{Rightarrow }}v$ sostiene. En otras palabras, $({stackrel {*}{Rightarrow }})$ y $({stackrel {+}{Rightarrow }})$ son el cierre transitivo reflexivo (que permite que una cadena se rinda) y el cierre transitivo (que requiere al menos un paso) de $(Rightarrow)$ , respectivamente.

Lenguaje libre de contexto

El idioma de una gramática $G=(V,SigmaR,S)$ es el conjunto

L(G)={win Sigma ^{*}:S{stackrel {*}{Rightarrow }}w}

de todas las cadenas de símbolos terminales derivables del símbolo de inicio.

Un idioma $L$ se dice que es un lenguaje libre de contexto (CFL), si existe un CFG $G$ , tal que $L,=,L(G)$ .

Los autómatas pushdown no deterministas reconocen exactamente los lenguajes libres de contexto.

Ejemplos

Palabras concatenadas con su reverso

La gramática $G=({S},{a,b},P,S)$ , con producciones

S \to aSa

S \to b Sb

S \to ε

es independiente del contexto. No es propio ya que incluye una producción de ε. Una derivación típica en esta gramática es

S \to aSa \to aaSaa \to aabSbaa \to aabbaa

Esto deja claro que $L(G)={ww^{R}:win {a,b}^{*}}$ . El lenguaje es libre de contextos, sin embargo, se puede probar que no es regular.

Si las producciones

S \to a

S \to b

se añade, una gramática libre de contexto para el conjunto de todos los palíndromos sobre el alfabeto ${a, b}$ se obtiene.

Paréntesis bien formados

El ejemplo canónico de una gramática independiente del contexto es la coincidencia de paréntesis, que es representativa del caso general. Hay dos símbolos de terminal "(" y ")" y un símbolo no terminal S. Las reglas de producción son

S \to SS

S \to S)

S \to ()

La primera regla permite que el símbolo S se multiplique; la segunda regla permite que el símbolo S se encierre entre paréntesis correspondientes; y la tercera regla termina la recursividad.

Paréntesis anidados y corchetes bien formados

Un segundo ejemplo canónico son dos tipos diferentes de paréntesis anidados coincidentes, descritos por las producciones:

S \to SS

S \to ()

S \to S)

S \to

S \to S]

con símbolos de terminal [ ] () y S no terminal.

La siguiente secuencia se puede derivar en esa gramática:

[ [ [ [ [ ()(] ] ] ] [ ] ] ]

Pares coincidentes

En una gramática independiente del contexto, podemos emparejar caracteres como lo hacemos con los corchetes. El ejemplo más simple:

S \to aSb

S \to ab

Esta gramática genera el lenguaje ${a^{n}b^{n}:ngeq 1}$ , que no es regular (según el lema de bombeo para los idiomas regulares).

El carácter especial ε representa la cadena vacía. Al cambiar la gramática anterior a

S \to aSb

S \to ε

obtenemos una gramática generando el lenguaje ${a^{n}b^{n}:ngeq 0}$ en su lugar. Esto difiere sólo en que contiene la cadena vacía mientras que la gramática original no.

Número distinto de a's y b's

Una gramática independiente del contexto para el idioma que consta de todas las cadenas sobre {a,b} que contienen un número desigual de a y b:

S \to T \leftarrow U

T \to VaT \leftarrow VaV Silencioso TaV

U \to VbU Silencio VbV

V \to aVbV Silencioso bVaV

Aquí, la T no terminal puede generar todas las cadenas con más a's que b's, la U no terminal genera todas las cadenas con más b's que a's y la V no terminal genera todas las cadenas con el mismo número de a's y b's. Omitir la tercera alternativa en las reglas para T y U no restringe el lenguaje de la gramática.

Segundo bloque de b's de doble tamaño

Otro ejemplo de un lenguaje no regular es ${displaystyle {{text{b}}^{n}{text{a}}^{m}{text{b}}^{2n}:ngeq 0,mgeq 0}}$ . Es libre de contexto como puede ser generado por la siguiente gramática sin contexto:

S \to b Sbb Silencio A

A \to aA Silencio ε

Fórmulas lógicas de primer orden

Las reglas de formación de los términos y fórmulas de la lógica formal se ajustan a la definición de gramática independiente del contexto, excepto que el conjunto de símbolos puede ser infinito y puede haber más de un símbolo de inicio.

Ejemplos de lenguajes que no están libres de contexto

A diferencia de los paréntesis anidados y los corchetes bien formados de la sección anterior, no existe una gramática libre de contexto para generar todas las secuencias de dos tipos diferentes de paréntesis, cada uno balanceado por separado sin tener en cuenta al otro, donde los dos tipos no necesitan anidar uno dentro del otro, por ejemplo:

[)

[ [ [ [(()(] ] ]]))((([))(([))()()(])(])(])

El hecho de que este lenguaje no sea libre de contexto puede probarse utilizando lema de bombeo para lenguajes sin contexto y una prueba por contradicción, observando que todas las palabras de la forma ${displaystyle {(}^{n}{[}^{n}{)}^{n}{]}^{n}}$ debe pertenecer al lenguaje. Este idioma pertenece en vez de a una clase más general y puede ser descrito por una gramática conjuntiva, que a su vez también incluye otros lenguajes sin texto, como el lenguaje de todas las palabras de la forma ${displaystyle {text{a}}^{n}{text{b}}^{n}{text{c}}^{n}}$ .

Gramáticas regulares

Toda gramática regular es independiente del contexto, pero no todas las gramáticas independientes del contexto son regulares. La siguiente gramática libre de contexto, por ejemplo, también es regular.

S \to a

S \to aS

S \to bS

Los terminales aquí son $a$ y $b$ , mientras que el único nonterminal es $S$ . El idioma descrito es todas las cadenas no vacías de $a$ s $b$ s that end in $a$ .

Esta gramática es regular: ninguna regla tiene más de un no terminal en su lado derecho, y cada uno de estos no terminales está en el mismo extremo del lado derecho.

Toda gramática regular corresponde directamente a un autómata finito no determinista, por lo que sabemos que se trata de un lenguaje regular.

Usando barras verticales, la gramática anterior se puede describir más brevemente de la siguiente manera:

S \to a Silencio aS Silencio bS

Derivaciones y árboles sintácticos

Una derivación de una cadena para una gramática es una secuencia de aplicaciones de reglas gramaticales que transforman el símbolo de inicio en la cadena. Una derivación prueba que la cadena pertenece al lenguaje de la gramática.

Una derivación se determina completamente dando, para cada paso:

la norma aplicada en ese paso
la ocurrencia de su lado izquierdo al que se aplica

Para mayor claridad, también se suele dar la cadena intermedia.

Por ejemplo, con la gramática:

$S \to S + S$
$S \to 1$
$S \to a$

la cadena

1 + 1 + a

se puede derivar del símbolo de inicio $S$ con la siguiente derivación:

S

\to S + S

(por regla 1.

S

)

\to S + S + S

(por regla 1. en el segundo

S

)

\to 1 + S + S

(por regla 2. en la primera

S

)

\to 1 + 1 + S

(por regla 2. en el segundo

S

)

\to 1 + 1 + a

(por regla 3) en la tercera

S

)

A menudo, se sigue una estrategia que elige de forma determinista el siguiente no terminal para reescribir:

en una derivación más izquierda, es siempre el no terminal más izquierdo;
en una derivación más derecha, siempre es el no final más adecuado.

Dada tal estrategia, una derivación está completamente determinada por la secuencia de reglas aplicadas. Por ejemplo, una derivación más a la izquierda de la misma cadena es

S

\to S + S

(por regla 1 en la izquierda

S

)

\to 1 + S

(por regla 2 en la izquierda

S

)

\to 1 + S + S

(por regla 1 en la izquierda

S

)

\to 1 + 1 + S

(por regla 2 en la izquierda

S

)

\to 1 + 1 + a

(por regla 3 en la izquierda

S

que se puede resumir como

Artículo 1

Artículo 2

Artículo 1

Artículo 2

Artículo 3.

Una derivación más a la derecha es:

S

\to S + S

(por regla 1 sobre la derecha

S

)

\to S + S + S

(por regla 1 sobre la derecha

S

)

\to S + S + a

(por regla 3 sobre la derecha

S

)

\to S + 1 + a

(por regla 2 sobre la derecha

S

)

\to 1 + 1 + a

(por regla 2 sobre la derecha

S

que se puede resumir como

Artículo 1

Artículo 3

Artículo 2

Artículo 2.

La distinción entre la derivación más a la izquierda y la derivación más a la derecha es importante porque en la mayoría de los analizadores, la transformación de la entrada se define proporcionando una pieza de código para cada regla gramatical que se ejecuta cada vez que se aplica la regla. Por lo tanto, es importante saber si el analizador determina una derivación más a la izquierda o más a la derecha porque esto determina el orden en el que se ejecutarán las piezas de código. Consulte un ejemplo de analizadores LL y analizadores LR.

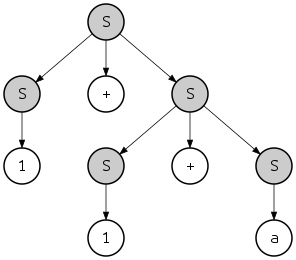
Una derivación también impone, en cierto sentido, una estructura jerárquica en la cadena que se deriva. Por ejemplo, si la cadena "1 + 1 + a" se deriva de acuerdo con la derivación más a la izquierda descrita anteriormente, la estructura de la cadena sería:

{{1} S + {{1} S + {a} S} S} S

donde ${...} S$ indica una subcadena reconocida como perteneciente a <span class="texhtml" S. Esta jerarquía también se puede ver como un árbol:

Este árbol se llama árbol de análisis o "árbol de sintaxis concreta" de la cadena, en contraste con el árbol de sintaxis abstracta. En este caso, las derivaciones presentadas más a la izquierda y más a la derecha definen el mismo árbol de análisis; sin embargo, hay otra derivación más a la derecha de la misma cadena

S

\to S + S

(por regla 1 sobre la derecha

S

)

\to S + a

(por regla 3 sobre la derecha

S

)

\to S + S + a

(por regla 1 sobre la derecha

S

)

\to S + 1 + a

(por regla 2 sobre la derecha

S

)

\to 1 + 1 + a

(por regla 2 sobre la derecha

S

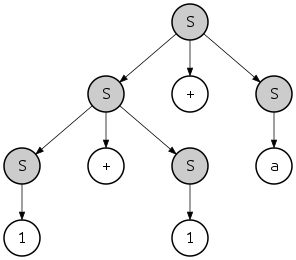
que define una cadena con una estructura diferente

{{1} S + {1} S} S + {a} S} S

y un árbol de análisis diferente:

Sin embargo, tenga en cuenta que ambos árboles de análisis se pueden obtener mediante derivaciones tanto a la izquierda como a la derecha. Por ejemplo, el último árbol se puede obtener con la derivación más a la izquierda de la siguiente manera:

S

\to S + S

(por regla 1 en la izquierda

S

)

\to S + S + S

(por regla 1 en la izquierda

S

)

\to 1 + S + S

(por regla 2 en la izquierda

S

)

\to 1 + 1 + S

(por regla 2 en la izquierda

S

)

\to 1 + 1 + a

(por regla 3 en la izquierda

S

Si una cadena en el lenguaje de la gramática tiene más de un árbol de análisis, entonces se dice que la gramática es una gramática ambigua. Estas gramáticas suelen ser difíciles de analizar porque el analizador no siempre puede decidir qué regla gramatical tiene que aplicar. Por lo general, la ambigüedad es una característica de la gramática, no del lenguaje, y se puede encontrar una gramática inequívoca que genera el mismo lenguaje libre de contexto. Sin embargo, hay ciertos lenguajes que solo pueden ser generados por gramáticas ambiguas; estos lenguajes se denominan lenguajes inherentemente ambiguos.

Ejemplo: expresiones algebraicas

Aquí hay una gramática libre de contexto para expresiones algebraicas con infijos sintácticamente correctas en las variables x, y y z:

$S \to x$
$S \to Sí.$
$S \to z$
$S \to S + S$
$S \to S - S$
$S \to S * S$
$S \to S / S$
$S \to S)$

Esta gramática puede, por ejemplo, generar la cadena

() x + Sí. * x - z * Sí. / x + x)

como sigue:

S

\to S - S

(por regla 5)

\to S * S - S

(por regla 6, aplicada a la izquierda

S

)

\to S * S - S / S

(por regla 7, aplicado a la derecha

S

)

\to S * S - S / S

(por regla 8, aplicada a la izquierda

S

)

\to S * S - S / S)

(por regla 8, aplicado a la derecha

S

)

\to S + S * S - S / S)

(por regla 4, aplicado a la izquierda

S

)

\to S + S * S - S * S / S)

(por regla 6, aplicada al cuarto

S

)

\to S + S * S - S * S / S + S)

(por regla 4, aplicado a la derecha

S

)

\to x + S * S - S * S / S + S)

(etc.)

\to x + Sí. * S - S * S / S + S)

\to x + Sí. * x - S * S / S + S)

\to x + Sí. * x - z * S / S + S)

\to x + Sí. * x - z * Sí. / S + S)

\to x + Sí. * x - z * Sí. / x + S)

\to x + Sí. * x - z * Sí. / x + x)

Tenga en cuenta que se tomaron muchas decisiones en cuanto a qué reescritura se realizaría a continuación. Estas elecciones parecen bastante arbitrarias. De hecho, lo son, en el sentido de que la cadena finalmente generada es siempre la misma. Por ejemplo, la segunda y tercera reescritura

\to S * S - S

(por regla 6, aplicada a la izquierda

S

)

\to S * S - S / S

(por regla 7, aplicado a la derecha

S

)

podría hacerse en el orden opuesto:

\to S - S / S

(por regla 7, aplicado a la derecha

S

)

\to S * S - S / S

(por regla 6, aplicada a la izquierda

S

)

Además, se tomaron muchas decisiones sobre qué regla aplicar a cada $S$ seleccionado. Cambiar las elecciones hechas y no solo el orden en que se hicieron generalmente afecta qué cadena de terminal sale al final.

Veamos esto con más detalle. Considere el árbol de análisis de esta derivación:

Comenzando en la parte superior, paso a paso, se expande una S en el árbol, hasta que no queden más $S$ es (no terminales) sin expandir. Elegir un orden diferente de expansión producirá una derivación diferente, pero el mismo árbol de análisis. El árbol de análisis solo cambiará si elegimos una regla diferente para aplicar en alguna posición en el árbol.

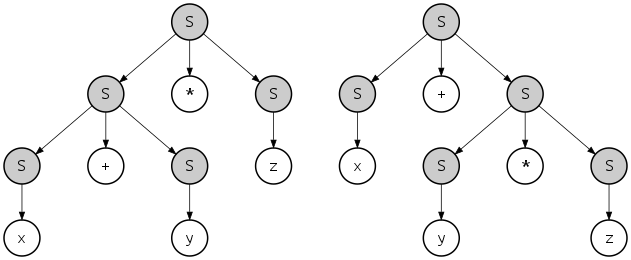
Pero, ¿puede un árbol de análisis diferente producir la misma cadena terminal, que es $(x + y) * x - z * y / (x + x)$ en este caso? Sí, para esta gramática particular, esto es posible. Las gramáticas con esta propiedad se denominan ambiguas.

Por ejemplo, $x + y * z$ se puede producir con estos dos diferentes árboles de análisis:

Sin embargo, el lenguaje descrito por esta gramática no es inherentemente ambiguo: se puede dar una gramática alternativa e inequívoca para el idioma, por ejemplo:

T \to x

T \to Sí.

T \to z

S \to S + T

S \to S - T

S \to S * T

S \to S / T

T \to S)

S \to T

una vez más seleccionando $S$ como símbolo de inicio. Esta gramática alternativa producirá $x + y * z$ con un árbol de análisis sintáctico similar al dejó uno arriba, es decir, asumiendo implícitamente la asociación $(x + y) * z$ , que no sigue el orden estándar de las operaciones. Se pueden construir gramáticas más elaboradas, inequívocas y libres de contexto que produzcan árboles de análisis sintáctico que obedezcan todas las reglas deseadas de asociatividad y precedencia de operadores.

Formas normales

Toda gramática independiente del contexto sin producción de ε tiene una gramática equivalente en la forma normal de Chomsky y una gramática en la forma normal de Greibach. "Equivalente" aquí significa que las dos gramáticas generan el mismo lenguaje.

La forma especialmente simple de las reglas de producción en las gramáticas de forma normal de Chomsky tiene implicaciones tanto teóricas como prácticas. Por ejemplo, dada una gramática libre de contexto, se puede usar la forma normal de Chomsky para construir un algoritmo de tiempo polinomial que decida si una cadena determinada está en el lenguaje representado por esa gramática o no (el algoritmo CYK).

Propiedades de cierre

Los lenguajes libres de contexto se cierran bajo varias operaciones, es decir, si los lenguajes K y L son libre de contexto, también lo es el resultado de las siguientes operaciones:

sindicato K ∪ L; concatenación K ∘ L; estrella kleene L^*
sustitución (en particular el homomorfismo)
homomorfismo inverso
intersección con un idioma regular

No están cerrados bajo la intersección general (por lo tanto, tampoco bajo la complementación) y la diferencia de conjuntos.

Problemas decidibles

Los siguientes son algunos problemas decidibles sobre gramáticas independientes del contexto.

Análisis

El problema de análisis, comprobar si una palabra dada pertenece al idioma dado por una gramática libre de contexto, es decidible, utilizando uno de los algoritmos de análisis de propósito general:

algoritmo CYK (para gramáticas en forma normal Chomsky)
Earley Parser
GLR parser
Parser LL (sólo para la subclase adecuada de LL(kGramáticas)

Leslie G. Valiant demostró que el análisis sin contexto para las gramáticas de forma normal de Chomsky se puede reducir a la multiplicación de matrices booleanas, heredando así su límite superior de complejidad de O(n^2.3728639). Por el contrario, Lillian Lee ha demostrado que la multiplicación de matrices booleanas O(n^3−ε) es reducible a O(n^3−3ε) análisis de CFG, estableciendo así algún tipo de límite inferior para este último.

Accesibilidad, productividad, nulabilidad

Gramática de ejemplo:
S → Bb Silencio Cc Silencio Ee
B → Bb Silencio b
C → C
D → Bd Silencio Cd Silencio d
E → Ee

Un símbolo no definitivo $X$ se llama productivo, o generación, si hay una derivación ${displaystyle X{stackrel {*}{Rightarrow }}w}$ para alguna cuerda $w$ de símbolos terminales. $X$ se llama accesible si hay una derivación ${displaystyle S{stackrel {*}{Rightarrow }}alpha Xbeta }$ para algunas cuerdas $alphabeta$ de símbolos no terminales y terminales del símbolo de inicio. $X$ se llama inútil inútil inútil inútil inútil inútil inútil inútil inútil si es inalcanzable o improductivo. $X$ se llama nulo si hay una derivación ${displaystyle X{stackrel {*}{Rightarrow }}varepsilon }$ . Una regla ${displaystyle Xrightarrow varepsilon }$ se llama ε-producción. Una derivación ${displaystyle X{stackrel {+}{Rightarrow }}X}$ se llama ciclo.

Se sabe que los algoritmos eliminan de una gramática dada, sin cambiar su lenguaje generado,

símbolos improductivos,
símbolos inalcanzables,
ε-productions, with one possible exception, and
ciclos.

En particular, una alternativa que contenga un símbolo no terminal inútil se puede eliminar del lado derecho de una regla. Tales reglas y alternativas se denominan inútiles.

En el ejemplo de gramática representado, la D no terminal es inalcanzable y E es improductiva, mientras que C → C provoca un ciclo. Por lo tanto, la omisión de las tres últimas reglas no cambia el lenguaje generado por la gramática, ni la omisión de las alternativas "| CC | Ee" del lado derecho de la regla para S.

Se dice que una gramática independiente del contexto es adecuada si no tiene símbolos inútiles ni producciones ε ni ciclos. Combinando los algoritmos anteriores, cada gramática libre de contexto que no genera ε puede transformarse en una gramática propia débilmente equivalente.

Comprobaciones de regularidad y LL(k)

Es decidible si una gramática dada es una gramática regular, así como si es una gramática LL(k) para una k≥0 dada. Si no se da k, el último problema es indecidible.

Dado un lenguaje libre de contexto, no es decidible si es regular, ni si es un lenguaje LL(k) para un k dado .

Vacío y finitud

Existen algoritmos para decidir si un idioma de un determinado idioma libre de contexto está vacío, así como si es finito.

Problemas indecidibles

Algunas preguntas que son indecidibles para clases más amplias de gramáticas se vuelven decidibles para gramáticas independientes del contexto; p.ej. el problema del vacío (si la gramática genera alguna cadena terminal), es indecidible para las gramáticas sensibles al contexto, pero decidible para las gramáticas independientes del contexto.

Sin embargo, muchos problemas son indecidibles incluso para gramáticas independientes del contexto. Los ejemplos son:

Universalidad

Dado un CFG, ¿genera el lenguaje de todas las cadenas sobre el alfabeto de los símbolos terminales usados en sus reglas?

Se puede demostrar una reducción de este problema a partir del conocido problema indecidible de determinar si una máquina de Turing acepta una entrada en particular (el problema de detención). La reducción utiliza el concepto de un historial de cómputo, una cadena que describe un cómputo completo de una máquina de Turing. Se puede construir un CFG que genera todas las cadenas que no aceptan historiales de cómputo para una máquina de Turing particular en una entrada particular y, por lo tanto, aceptará todas las cadenas solo si la máquina no acepta esa entrada.

Igualdad lingüística

Dados dos CFG, ¿generan el mismo idioma?

La indecidibilidad de este problema es una consecuencia directa del anterior: es imposible siquiera decidir si un CFG es equivalente al trivial CFG que define el lenguaje de todas las cadenas.

Inclusión de idiomas

Dados dos CFG, ¿puede el primero generar todas las cadenas que puede generar el segundo?

Si este problema fuera decidible, entonces la igualdad lingüística también podría decidirse: dos CFG G1 y G2 generan el mismo idioma si L(G1) es un subconjunto de L(G2) y L(G2) es un subconjunto de L(G1).

Estar en un nivel inferior o superior de la jerarquía de Chomsky

Usando el teorema de Greibach, se puede demostrar que los dos problemas siguientes son indecidibles:

Dada una gramática sensible al contexto, ¿describe un lenguaje sin contexto?
Dada una gramática sin contexto, ¿describe un lenguaje regular?

Ambigüedad gramatical

Dado un CFG, ¿es ambiguo?

La indecidibilidad de este problema se deriva del hecho de que si existiera un algoritmo para determinar la ambigüedad, se podría decidir el problema de la correspondencia Post, que se sabe que es indecidible.

Desconecte del lenguaje

Dados dos CFG, ¿hay alguna cadena derivable de ambas gramáticas?

Si este problema fuera decidable, también se podría decidir el problema indecidable de la correspondencia postal: dadas las cuerdas $alpha _{1},ldotsalpha _{N},beta _{1},ldotsbeta _{N}$ sobre un alfabeto ${a_{1},ldotsa_{k}}$ , deja la gramática $G_{1}$ consiste en la regla

Sto alpha _{1}Sbeta _{1}^{rev}|cdots |alpha _{N}Sbeta _{N}^{rev}|b

;

Donde $beta _{i}^{rev}$ denota la cadena inversa $beta _{i}$ y $b$ no ocurre entre $a_{i}$ ; y dejar gramática $G_{2}$ consiste en la regla

Tto a_{1}Ta_{1}|cdots |a_{k}Ta_{k}|b

;

Luego el problema de correo dado por $alpha _{1},ldotsalpha _{N},beta _{1},ldotsbeta _{N}$ tiene una solución si y sólo si $L(G_{1})$ y $L(G_{2})$ compartir una cadena derivada.

Extensiones

Una manera obvia de extender el formalismo gramatical independiente del contexto es permitir que los no terminales tengan argumentos, cuyos valores se transmiten dentro de las reglas. Esto permite que las características del lenguaje natural, como el acuerdo y la referencia, y los análogos del lenguaje de programación, como el uso correcto y la definición de identificadores, se expresen de forma natural. P.ej. ahora podemos expresar fácilmente que en las oraciones en inglés, el sujeto y el verbo deben concordar en número. En informática, los ejemplos de este enfoque incluyen gramáticas de afijos, gramáticas de atributos, gramáticas indexadas y gramáticas de dos niveles de Van Wijngaarden. Extensiones similares existen en lingüística.

Una gramática libre de contexto extendida (o gramática regular de la parte derecha) es aquella en la que se permite que el lado derecho de las reglas de producción sea una expresión regular sobre los terminales y no terminales de la gramática. Las gramáticas libres de contexto extendidas describen exactamente los lenguajes libres de contexto.

Otra extensión es permitir que aparezcan símbolos terminales adicionales en el lado izquierdo de las reglas, restringiendo su aplicación. Esto produce el formalismo de las gramáticas sensibles al contexto.

Subclases

Hay varias subclases importantes de las gramáticas independientes del contexto:

Las gramáticas LR(k) (también conocidas como gramáticas libres de contexto determinista) permiten la parsing (reconocimiento de cuerda) con automata de empuje determinista (PDA), pero sólo pueden describir lenguajes deterministas libres de contexto.
Simple LR, Look-Ahead Las gramáticas LR son subclases que permiten una mayor simplificación de la parsing. SLR y LALR son reconocidos usando el mismo PDA que LR, pero con tablas más simples, en la mayoría de los casos.
Las gramáticas LL(k) y LL(*) permiten el análisis mediante la construcción directa de una derivación más izquierda como se describe anteriormente, y describen incluso menos idiomas.
Las gramáticas simples son una subclase de las gramáticas LL(1) sobre todo interesantes para su propiedad teórica que la igualdad de lenguaje de gramáticas simples es decidable, mientras que la inclusión del lenguaje no es.
Las gramáticas trenzadas tienen la propiedad que los símbolos terminales se dividen en pares de corchetes izquierdo y derecho que siempre coinciden con las reglas.
Las gramáticas lineales no tienen reglas con más de un no-terminal en el lado derecho.
Las gramáticas regulares son una subclase de las gramáticas lineales y describen los idiomas regulares, es decir, corresponden a automata finita y expresiones regulares.

El análisis LR amplía el análisis LL para admitir una mayor variedad de gramáticas; a su vez, el análisis LR generalizado amplía el análisis LR para admitir gramáticas libres de contexto arbitrarias. En gramáticas LL y gramáticas LR, esencialmente realiza análisis sintáctico LL y análisis sintáctico LR, respectivamente, mientras que en gramáticas no deterministas, es tan eficiente como se puede esperar. Aunque el análisis sintáctico GLR se desarrolló en la década de 1980, muchas nuevas definiciones de lenguaje y generadores de analizadores continúan basándose en el análisis sintáctico LL, LALR o LR hasta el día de hoy.

Aplicaciones lingüísticas

Chomsky inicialmente esperaba superar las limitaciones de las gramáticas independientes del contexto agregando reglas de transformación.

Tales reglas son otro dispositivo estándar en la lingüística tradicional; p.ej. pasivización en inglés. Gran parte de la gramática generativa se ha dedicado a encontrar formas de refinar los mecanismos descriptivos de la gramática de estructura sintagmática y las reglas de transformación de modo que se puedan expresar exactamente los tipos de cosas que el lenguaje natural realmente permite. Permitir transformaciones arbitrarias no cumple con ese objetivo: son demasiado poderosas y Turing es completa a menos que se agreguen restricciones significativas (por ejemplo, no hay transformaciones que introduzcan y luego reescriban símbolos sin contexto).

La posición general de Chomsky con respecto a la falta de contexto del lenguaje natural se ha mantenido desde entonces, aunque sus ejemplos específicos con respecto a la inadecuación de las gramáticas libres de contexto en términos de su débil capacidad generativa fueron posteriormente refutados. Gerald Gazdar y Geoffrey Pullum han argumentado que, a pesar de algunas construcciones no independientes del contexto en el lenguaje natural (como las dependencias entre series en el alemán suizo y la reduplicación en bambara), la gran mayoría de las formas en el lenguaje natural son, de hecho, independientes del contexto.

Te puede interesar
Aridad
(leer más)
Te puede interesar
Animación por computadora
(leer más)
Te puede interesar
Búsqueda en amplitud
(leer más)
Más resultados...

Gramática libre de contexto

Antecedentes

Definiciones formales

Notación de regla de producción

Aplicación de reglas

Aplicación de regla repetitiva

Lenguaje libre de contexto

Ejemplos

Palabras concatenadas con su reverso

Paréntesis bien formados

Paréntesis anidados y corchetes bien formados

Pares coincidentes

Número distinto de a's y b's

Segundo bloque de b's de doble tamaño

Fórmulas lógicas de primer orden

Ejemplos de lenguajes que no están libres de contexto

Gramáticas regulares

Derivaciones y árboles sintácticos

Ejemplo: expresiones algebraicas

Formas normales

Propiedades de cierre

Problemas decidibles

Análisis

Accesibilidad, productividad, nulabilidad

Comprobaciones de regularidad y LL(k)

Vacío y finitud

Problemas indecidibles

Universalidad

Igualdad lingüística

Inclusión de idiomas

Estar en un nivel inferior o superior de la jerarquía de Chomsky

Ambigüedad gramatical

Desconecte del lenguaje

Extensiones

Subclases

Aplicaciones lingüísticas

Aridad

Animación por computadora

Búsqueda en amplitud