Gráfico Q-Q

En estadística, un gráfico Q–Q (gráfico cuantil-cuantil) es un gráfico de probabilidad, un método gráfico para comparar dos distribuciones de probabilidad trazando sus cuantiles entre sí. Un punto (x, y) en el gráfico corresponde a uno de los cuantiles de la segunda distribución ((x, y) en el gráfico ="texhtml">y-coordinada) trazada contra el mismo cuantil de la primera distribución (x -coordinar). Esto define una curva paramétrica donde el parámetro es el índice del intervalo cuantil.

Si las dos distribuciones que se comparan son similares, los puntos en el gráfico Q-Q se ubicarán aproximadamente en la línea de identidad y = x. Si las distribuciones están relacionadas linealmente, los puntos en el gráfico Q-Q estarán aproximadamente en una línea, pero no necesariamente en la línea y = x. Los gráficos Q – Q también se pueden utilizar como medio gráfico para estimar parámetros en una familia de distribuciones a escala de ubicación.

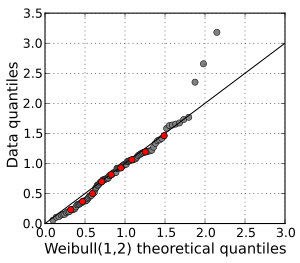
Se utiliza un gráfico Q-Q para comparar las formas de las distribuciones, lo que proporciona una vista gráfica de cómo propiedades como la ubicación, la escala y la asimetría son similares o diferentes en las dos distribuciones. Los gráficos Q-Q se pueden utilizar para comparar colecciones de datos o distribuciones teóricas. El uso de gráficos Q-Q para comparar dos muestras de datos puede verse como un enfoque no paramétrico para comparar sus distribuciones subyacentes. Un gráfico Q-Q es generalmente más diagnóstico que comparar las muestras. histogramas, pero es menos conocido. Los gráficos Q-Q se utilizan comúnmente para comparar un conjunto de datos con un modelo teórico. Esto puede proporcionar una evaluación de la bondad del ajuste que sea gráfica, en lugar de reducirse a una estadística resumida numérica. Los gráficos Q – Q también se utilizan para comparar dos distribuciones teóricas entre sí. Dado que los gráficos Q-Q comparan distribuciones, no es necesario observar los valores como pares, como en un gráfico de dispersión, ni siquiera que el número de valores en los dos grupos que se comparan sea igual.

El término "gráfico de probabilidad" a veces se refiere específicamente a un gráfico Q-Q, a veces a una clase más general de gráficos y, a veces, al gráfico P-P, menos utilizado. El gráfico de coeficiente de correlación del gráfico de probabilidad (gráfico PPCC) es una cantidad derivada de la idea de los gráficos Q – Q, que mide la concordancia de una distribución ajustada con los datos observados y que a veces se utiliza como medio para ajustar una distribución a los datos.

Un gráfico Q–Q es un gráfico de los cuantiles de dos distribuciones entre sí, o un gráfico basado en estimaciones de los cuantiles. El patrón de puntos en el gráfico se utiliza para comparar las dos distribuciones.

El paso principal en la construcción de un gráfico Q–Q es calcular o estimar los cuantiles que se van a representar. Si uno o ambos ejes en un gráfico Q-Q se basa en una distribución teórica con una función de distribución acumulativa (CDF) continua, todos los cuantiles están definidos de forma única y se pueden obtener invirtiendo la CDF. Si una distribución de probabilidad teórica con una CDF discontinua es una de las dos distribuciones que se comparan, es posible que algunos de los cuantiles no estén definidos, por lo que se puede trazar un cuantil interpolado. Si el gráfico Q-Q se basa en datos, se utilizan múltiples estimadores cuantiles. Las reglas para formar gráficos Q – Q cuando se deben estimar o interpolar cuantiles se denominan posiciones de trazado.

Un caso simple es aquel en el que se tienen dos conjuntos de datos del mismo tamaño. En ese caso, para hacer el gráfico Q-Q, se ordena cada conjunto en orden creciente, luego se emparejan y se trazan los valores correspondientes. Una construcción más complicada es el caso en el que se comparan dos conjuntos de datos de diferentes tamaños. Para construir el gráfico Q–Q en este caso, es necesario utilizar una estimación cuantil interpolada para que se puedan construir los cuantiles correspondientes a la misma probabilidad subyacente.

De manera más abstracta, dadas dos funciones de distribución de probabilidad acumulativa F y G< /span>, con funciones cuantiles asociadas F⁻¹ y G ⁻¹ (la función inversa de la CDF es la función cuantil), el gráfico Q–Q dibuja el q-ésimo cuantil de F frente al q< /span>-ésimo cuantil de G para un rango de valores de q< /lapso>. Por tanto, la gráfica Q–Q es una curva paramétrica indexada sobre [0,1] con valores en el plano real R².

Los puntos trazados en un gráfico Q–Q siempre son no decrecientes cuando se ven de izquierda a derecha. Si las dos distribuciones que se comparan son idénticas, el gráfico Q-Q sigue la línea de 45° y = x. Si las dos distribuciones concuerdan después de transformar linealmente los valores en una de las distribuciones, entonces el gráfico Q-Q sigue alguna línea, pero no necesariamente la línea y = x. Si la tendencia general del gráfico Q–Q es más plana que la línea y = x, la distribución trazada en el El eje horizontal está más disperso que la distribución trazada en el eje vertical. Por el contrario, si la tendencia general del gráfico Q–Q es más pronunciada que la línea y = x, la distribución trazada en el eje vertical está más dispersa que la distribución trazada en el eje horizontal. Los gráficos Q-Q suelen tener forma de arco o de S, lo que indica que una de las distribuciones está más sesgada que la otra, o que una de las distribuciones tiene colas más pesadas que la otra.

Aunque un gráfico Q–Q se basa en cuantiles, en un gráfico Q–Q estándar no es posible determinar qué punto del gráfico Q–Q determina un cuantil determinado. Por ejemplo, no es posible determinar la mediana de cualquiera de las dos distribuciones que se comparan inspeccionando el gráfico Q-Q. Algunos gráficos Q–Q indican los deciles para hacer posibles determinaciones como ésta.

La intersección y la pendiente de una regresión lineal entre los cuantiles dan una medida de la ubicación relativa y la escala relativa de las muestras. Si la mediana de la distribución trazada en el eje horizontal es 0, la intersección de una línea de regresión es una medida de ubicación y la pendiente es una medida de escala. La distancia entre medianas es otra medida de ubicación relativa reflejada en un gráfico Q-Q. El "coeficiente de correlación del gráfico de probabilidad" (Gráfico PPCC) es el coeficiente de correlación entre los cuantiles de muestras pareadas. Cuanto más cerca esté el coeficiente de correlación de uno, más cerca estarán las distribuciones de ser versiones desplazadas y escaladas entre sí. Para distribuciones con un solo parámetro de forma, el gráfico de probabilidad del coeficiente de correlación proporciona un método para estimar el parámetro de forma: uno simplemente calcula el coeficiente de correlación para diferentes valores del parámetro de forma y usa el que tiene el mejor ajuste, como si Estaban comparando distribuciones de diferentes tipos.

Otro uso común de los gráficos Q–Q es comparar la distribución de una muestra con una distribución teórica, como la distribución normal estándar N(0,1 ), como en un gráfico de probabilidad normal. Como en el caso de comparar dos muestras de datos, uno ordena los datos (formalmente, calcula las estadísticas de orden) y luego los representa frente a ciertos cuantiles de la distribución teórica.

La elección de quantiles de una distribución teórica puede depender del contexto y el propósito. Una opción, dada una muestra de tamaño n, es k / n para k = 1, ... n, como estos son los quantiles que la distribución de muestreo se da cuenta. El último de estos, n / n, corresponde al percentil 100 – el valor máximo de la distribución teórica, que a veces es infinita. Otras opciones son el uso de ()k 0,5 a 0) n, o en lugar de espacio el n puntos tales que hay una distancia igual entre todos ellos y también entre los dos puntos más exteriores y los bordes de los ${\displaystyle [0,1]}$ intervalo, utilizando k /n + 1).

Se han sugerido muchas otras opciones, tanto formales como heurísticas, basadas en teorías o simulaciones relevantes en el contexto. Las siguientes subsecciones analizan algunos de ellos. Una cuestión más concreta es elegir un máximo (estimación de un máximo de población), conocido como el problema de los tanques alemanes, para el cual se puede aplicar un "máximo de muestra más una brecha" Existen soluciones, la más simple es m + m/n − 1. Una aplicación más formal de esta uniformización del espaciamiento ocurre en la estimación del espaciamiento máximo de parámetros.

El enfoque k / (n + 1) equivale al de trazar los puntos según la probabilidad de que el El último de (n + 1) valores extraídos aleatoriamente no excederá el k< /span>-ésimo más pequeño de los primeros n valores extraídos aleatoriamente.

Al utilizar un gráfico de probabilidad normal, los cuantiles que se utilizan son los rankingits, el cuantil del valor esperado del estadístico de orden de una distribución normal estándar.

De manera más general, la prueba de Shapiro-Wilk utiliza los valores esperados de los estadísticos de orden de la distribución dada; el gráfico y la línea resultantes producen la estimación de mínimos cuadrados generalizados para la ubicación y la escala (a partir de la intersección y la pendiente de la línea ajustada). Aunque esto no es demasiado importante para la distribución normal (la ubicación y la escala se estiman mediante la media y la desviación estándar, respectivamente), puede resultar útil para muchas otras distribuciones.

Sin embargo, esto requiere calcular los valores esperados del estadístico de orden, lo que puede resultar difícil si la distribución no es normal.

Alternativamente, se pueden utilizar estimaciones de la mediana de las estadísticas de orden, que se pueden calcular basándose en estimaciones de la mediana de las estadísticas de orden de una distribución uniforme y la función cuantil de la distribución; esto fue sugerido por Filliben (1975).

Esto se puede generar fácilmente para cualquier distribución para la cual se pueda calcular la función cuantil, pero a la inversa, las estimaciones resultantes de ubicación y escala ya no son precisamente estimaciones de mínimos cuadrados, aunque solo difieren significativamente para n pequeño.

Se han utilizado o propuesto varias fórmulas diferentes como posiciones de trazado simétricas afines. Estas fórmulas tienen la forma (k − a) / (n + 1 − 2a ) para algún valor de a en el rango de 0 a 1, lo que da un rango entre k / (n + 1) y (k − 1) / (n − 1).

Las expresiones incluyen:

• k /n + 1)
• ()k 0,3 a 0)n + 0.4).
• ()k − 0.3175) / (n + 0,365).
• ()k − 0.326) / (n + 0,348).
• ()k − 1⁄3) / (n + 1⁄3).
• ()k − 0,375)n + 0.25).
• ()k − 0,4) / (n + 0,2).
• ()k − 0,44) / (n + 0.12).
• ()k 0,5 a 0)n.
• ()k , 0,5 a 67)n − 0,134).
• ()k −1) /n −1).

Para muestras de gran tamaño, n, hay poca diferencia entre estas diversas expresiones.

Las medianas de las estadísticas de orden son las medianas de las estadísticas de orden de la distribución. Estos se pueden expresar en términos de la función cuantil y las medianas del estadístico de orden para la distribución uniforme continua mediante:

${\displaystyle N(i)=G(U(i)}$

donde U(i) son las medianas del estadístico de orden uniforme y < i>G es la función cuantil para la distribución deseada. La función cuantil es la inversa de la función de distribución acumulativa (probabilidad de que X sea menor o igual a algún valor). Es decir, dada una probabilidad, queremos el cuantil correspondiente de la función de distribución acumulativa.

James J. Filliben utiliza las siguientes estimaciones para las medianas del estadístico de orden uniforme:

${\displaystyle m(i)={\begin{cases}1-0.5^{1/n} limiti=1\\\\\\\\\\\\\\\\\dfrac {i-0.3175}{n+0.365}}} {\ldotsn-1\\\\\0.5^{1/n}}}}}}}$

La razón de esta estimación es que las medianas de las estadísticas de orden no tienen una forma simple.

El lenguaje de programación R viene con funciones para crear gráficos Q-Q, concretamente qqnorm y qqplot del estadísticas paquete. El paquete fastqq implementa un trazado más rápido para una gran cantidad de datos puntos.

• Función de distribución empírica
• El análisis Probit fue desarrollado por Chester Ittner Bliss en 1934.

• Parcela de probabilidad