Gráfico de probabilidad normal

El gráfico de probabilidad normal es una técnica gráfica para identificar desviaciones sustanciales de la normalidad. Esto incluye identificar valores atípicos, asimetría, curtosis, necesidad de transformaciones y mezclas. Los gráficos de probabilidad normal están hechos de datos sin procesar, residuos de ajustes del modelo y parámetros estimados.

En un gráfico de probabilidad normal (también llamado "gráfico normal"), los datos ordenados se trazan frente a los valores seleccionados para que la imagen resultante parezca cercana a una línea recta si los datos se distribuyen aproximadamente normalmente. Las desviaciones de una línea recta sugieren desviaciones de la normalidad. El trazado se puede realizar manualmente utilizando un papel cuadriculado especial, llamado papel de probabilidad normal. En las computadoras modernas, los gráficos normales se crean comúnmente con software.

El gráfico de probabilidad normal es un caso especial del gráfico de probabilidad Q–Q para una distribución normal. Los cuantiles teóricos generalmente se eligen para aproximarse a la media o la mediana de las estadísticas de orden correspondientes.

Definición

El gráfico de probabilidad normal se forma trazando los datos ordenados frente a una aproximación a las medias o medianas de las estadísticas de orden correspondientes; ver rankingit. Algunos trazan los datos en el eje vertical; otros trazan los datos en el eje horizontal.

Diferentes fuentes utilizan aproximaciones ligeramente diferentes para los rankingits. La fórmula utilizada por la "qqnorm" funcionan en las "estadísticas" El paquete en R (lenguaje de programación) es el siguiente:

${displaystyle z_{i}=Phi ^{-1}left({frac {i-a}{n+1-2a}right),}$

para i = 1, 2,..., n, dónde

a = 3/8 si n≤ 10 y

0,5 para nØ 10

y Φ⁻¹ es la función cuantil normal estándar.

Si los datos son consistentes con una muestra de una distribución normal, los puntos deben estar cerca de una línea recta. Como referencia se puede ajustar una línea recta a los puntos. Cuanto más se alejan los puntos de esta línea, mayor es el indicio de desviación de la normalidad. Si la muestra tiene media 0 y desviación estándar 1, entonces se podría utilizar una línea que pase por 0 con pendiente 1.

Con más puntos, las desviaciones aleatorias de una línea serán menos pronunciadas. Los gráficos normales se utilizan a menudo con tan solo 7 puntos, por ejemplo, para trazar los efectos en un modelo saturado de un experimento factorial fraccional de 2 niveles. Con menos puntos, resulta más difícil distinguir entre variabilidad aleatoria y una desviación sustancial de la normalidad.

Otras distribuciones

Los gráficos de probabilidad para distribuciones distintas a la normal se calculan exactamente de la misma manera. La función cuantil normal Φ⁻¹ simplemente se reemplaza por la función cuantil de la distribución deseada. De esta manera, se puede generar fácilmente un gráfico de probabilidad para cualquier distribución para la que se tenga la función cuantil.

Con una familia de distribuciones de ubicación-escala, los parámetros de ubicación y escala de la distribución se pueden estimar a partir de la intersección y la pendiente de la línea. Para otras distribuciones, primero se deben estimar los parámetros antes de poder realizar un gráfico de probabilidad.

Tipos de trama

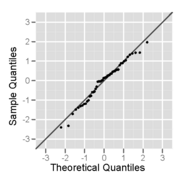
Ésta es una muestra de tamaño 50 de una distribución normal, trazada como histograma y como gráfico de probabilidad normal.

• 

  Parcela de probabilidad normal de una muestra de una distribución normal – se ve bastante recta, al menos cuando se ignoran los pocos valores grandes y pequeños.

• 

  Histograma de una muestra de una distribución normal – se ve bastante simétrico y unimodal

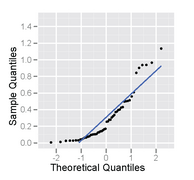
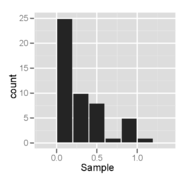
Esta es una muestra de tamaño 50 de una distribución sesgada a la derecha, trazada como un histograma y un gráfico de probabilidad normal.

• 

  Parcela de probabilidad normal de una muestra de una distribución derecha - tiene una forma C invertida.

• 

  Histograma de una muestra de una distribución hecha a la derecha – se ve unimodal y segado a la derecha.

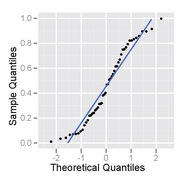
Esta é uma amostra de tamanho 50 de uma distribuição uniforme, plotada como um histograma e um gráfico de probabilidade normal.

• 

  Parcela de probabilidad normal de una muestra de una distribución uniforme – tiene una forma S.

• 

  Histograma de una muestra de una distribución uniforme – se ve multimodal y supuestamente simétrica.