Gráfico Acíclico Dirigido
En matemáticas, particularmente en teoría de grafos e informática, un gráfico acíclico dirigido (DAG) es un gráfico dirigido sin ciclos dirigidos. Es decir, consta de vértices y aristas (también llamados arcos), con cada arista dirigida de un vértice a otro, de modo que seguir esas direcciones nunca formará un bucle cerrado. Un grafo dirigido es un DAG si y solo si puede ordenarse topológicamente, organizando los vértices como un ordenamiento lineal que es consistente con todas las direcciones de los bordes. Los DAG tienen numerosas aplicaciones científicas y computacionales, que van desde la biología (evolución, árboles genealógicos, epidemiología) hasta la ciencia de la información (redes de citas) y la computación (programación).
Los gráficos acíclicos dirigidos a veces se denominan gráficos dirigidos acíclicos o dígrafos acíclicos.
Definiciones
Un grafo está formado por vértices y por aristas que conectan pares de vértices, donde los vértices pueden ser cualquier tipo de objeto que esté conectado en pares por aristas. En el caso de un grafo dirigido, cada arista tiene una orientación, de un vértice a otro vértice. Un camino en un gráfico dirigido es una secuencia de aristas que tiene la propiedad de que el vértice final de cada arista de la secuencia es el mismo que el vértice inicial de la siguiente arista de la secuencia; un camino forma un ciclo si el vértice inicial de su primera arista es igual al vértice final de su última arista. Un gráfico acíclico dirigido es un gráfico dirigido que no tiene ciclos.
Se dice que un vértice v de un grafo dirigido es accesible desde otro vértice u cuando existe una ruta que comienza en u y termina en v. Como caso especial, cada vértice se considera alcanzable desde sí mismo (por un camino con aristas cero). Si un vértice puede llegar a sí mismo a través de un camino no trivial (un camino con una o más aristas), entonces ese camino es un ciclo, por lo que otra forma de definir grafos acíclicos dirigidos es que son los gráficos en los que ningún vértice puede llegar a sí mismo a través de un camino no trivial.
Propiedades matemáticas
Relación de accesibilidad, cierre transitivo y reducción transitiva
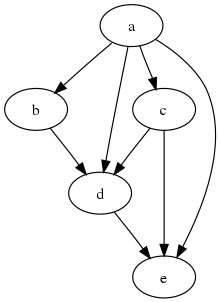
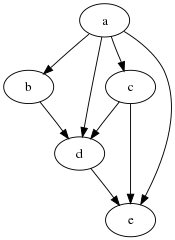
La relación de accesibilidad de un DAG se puede formalizar como un orden parcial ≤ en los vértices del DAG. En este orden parcial, dos vértices u y v se ordenan como u ≤ v exactamente cuando existe una ruta dirigida desde u a v en el DAG; es decir, cuando u puede llegar a v (o v es accesible desde u). Sin embargo, diferentes DAG pueden dar lugar a la misma relación de accesibilidad y al mismo orden parcial. Por ejemplo, un DAG con dos aristas u → v y v → w tiene la misma relación de accesibilidad que el DAG con tres aristas u → v, v → w y u → w. Ambos DAG producen el mismo orden parcial, en el que los vértices se ordenan como u ≤ v ≤ w.
El cierre transitivo de un DAG es el gráfico con la mayor cantidad de bordes que tiene la misma relación de accesibilidad que el DAG. Tiene una arista u → v para cada par de vértices (u, v) en la relación de accesibilidad ≤ del DAG y, por lo tanto, puede considerarse como una traducción directa de la relación de accesibilidad ≤ en términos teóricos de grafos. El mismo método de traducir órdenes parciales en DAG funciona de manera más general: para cada conjunto finito parcialmente ordenado (S, ≤), el gráfico que tiene un vértice para cada elemento de S y un borde para cada par de elementos en ≤ es automáticamente un DAG transitivamente cerrado y tiene (S, ≤) como su relación de accesibilidad. De esta forma, todo conjunto finito parcialmente ordenado se puede representar como un DAG.
La reducción transitiva de un DAG es el gráfico con la menor cantidad de aristas que tiene la misma relación de accesibilidad que el DAG. Tiene una arista u → v para cada par de vértices (u, v) en la relación de cobertura de la relación de accesibilidad ≤ del DAG. Es un subgrafo del DAG, formado al descartar los bordes u → v para los cuales el DAG también contiene un ruta dirigida desde u a v. Al igual que el cierre transitivo, la reducción transitiva se define de forma única para los DAG. Por el contrario, para un grafo dirigido que no es acíclico, puede haber más de un subgrafo mínimo con la misma relación de alcanzabilidad. Las reducciones transitivas son útiles para visualizar los órdenes parciales que representan, porque tienen menos bordes que otros gráficos que representan los mismos órdenes y, por lo tanto, conducen a dibujos de gráficos más simples. Un diagrama de Hasse de orden parcial es un dibujo de la reducción transitiva en el que se muestra la orientación de cada arista colocando el vértice inicial de la arista en una posición más baja que su vértice final.
Ordenación topológica
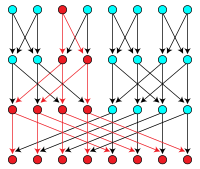
Una ordenación topológica de un grafo dirigido es una ordenación de sus vértices en una secuencia, de modo que para cada arista, el vértice inicial de la arista ocurre antes en la secuencia que el vértice final de la arista. Un gráfico que tiene un ordenamiento topológico no puede tener ningún ciclo, porque el borde hacia el vértice más antiguo de un ciclo tendría que estar orientado de manera incorrecta. Por lo tanto, todo grafo con un ordenamiento topológico es acíclico. Por el contrario, cada gráfico acíclico dirigido tiene al menos un ordenamiento topológico. Por lo tanto, la existencia de un ordenamiento topológico puede usarse como una definición equivalente de grafos acíclicos dirigidos: son exactamente los grafos que tienen ordenamientos topológicos. En general, este orden no es único; un DAG tiene un ordenamiento topológico único si y solo si tiene un camino dirigido que contiene todos los vértices, en cuyo caso el ordenamiento es el mismo que el orden en que aparecen los vértices en el camino.
La familia de órdenes topológicos de un DAG es la misma que la familia de extensiones lineales de la relación de accesibilidad para el DAG, por lo que dos gráficos que representan el mismo orden parcial tienen el mismo conjunto de órdenes topológicos.
Enumeración combinatoria
Robinson (1973) estudió el problema de enumeración de gráficos de contar gráficos acíclicos dirigidos. El número de DAG en n vértices etiquetados, para n = 0, 1, 2, 3, … (sin restricciones en el orden en que estos números aparecen en un orden topológico del DAG) es
- 1, 3, 25, 543, 29281, 3781503,... A003024 en el OEIS).
Estos números pueden ser calculados por la relación de recurrencia
- an=.. k=1n()− − 1)k− − 1()nk)2k()n− − k)an− − k.{displaystyle a_{n}=sum _{k=1}{n}(-1)^{k-1}{n choose k}2^{k(n-k)}a_{n-k}
Eric W. Weisstein conjeturó, y McKay et al. (2004) demostró que los mismos números cuentan las matrices (0,1) para las cuales todos los valores propios son números reales positivos. La prueba es biyectiva: una matriz A es una matriz de adyacencia de un DAG si y solo si A + I es una matriz (0,1) con todos los valores propios positivos, donde I denota la matriz de identidad. Debido a que un DAG no puede tener bucles automáticos, su matriz de adyacencia debe tener una diagonal cero, por lo que agregar I conserva la propiedad de que todas las matrices los coeficientes son 0 o 1.
Familias de grafos relacionados
Un árbol múltiple (también llamado grafo fuertemente inequívoco o manglar) es un DAG en el que hay como máximo una ruta dirigida entre dos vértices cualesquiera. De manera equivalente, es un DAG en el que el subgrafo accesible desde cualquier vértice induce un árbol no dirigido.
Un poliárbol (también llamado árbol dirigido) es un árbol múltiple formado al orientar los bordes de un árbol no dirigido.
Una arborescencia es un poliárbol formado al orientar los bordes de un árbol no dirigido lejos de un vértice en particular, llamado raíz de la arborescencia.
Problemas computacionales
Reconocimiento y clasificación topológica
La ordenación topológica es el problema algorítmico de encontrar una ordenación topológica de un DAG dado. Se puede resolver en tiempo lineal. El algoritmo de Kahn para la ordenación topológica crea la ordenación de vértices directamente. Mantiene una lista de vértices que no tienen aristas entrantes de otros vértices que aún no se han incluido en el ordenamiento topológico parcialmente construido; inicialmente, esta lista consiste en los vértices sin ningún borde entrante. Luego, agrega repetidamente un vértice de esta lista al final del ordenamiento topológico parcialmente construido y verifica si sus vecinos deben agregarse a la lista. El algoritmo termina cuando todos los vértices se han procesado de esta manera. Alternativamente, se puede construir un ordenamiento topológico invirtiendo una numeración posterior al orden de un recorrido de gráfico de búsqueda primero en profundidad.
También es posible verificar si un gráfico dirigido dado es un DAG en tiempo lineal, ya sea intentando encontrar un ordenamiento topológico y luego probando para cada borde si el ordenamiento resultante es válido o, alternativamente, para algunos algoritmos de ordenamiento topológico, al verificar que el algoritmo ordena con éxito todos los vértices sin cumplir una condición de error.
Construcción a partir de gráficas cíclicas
Cualquier gráfico no dirigido puede convertirse en un DAG eligiendo un orden total para sus vértices y dirigiendo cada borde desde el punto final anterior en el orden hasta el punto final posterior. La orientación resultante de los bordes se denomina orientación acíclica. Diferentes órdenes totales pueden conducir a la misma orientación acíclica, por lo que un gráfico de n-vértice puede tener menos de n! orientaciones acíclicas. El número de orientaciones acíclicas es igual a |χ(−1)|, donde χ es el polinomio cromático del gráfico dado.
Cualquier gráfico dirigido puede convertirse en un DAG eliminando un conjunto de vértices de retroalimentación o un conjunto de arcos de retroalimentación, un conjunto de vértices o aristas (respectivamente) que toca todos los ciclos. Sin embargo, el conjunto más pequeño de este tipo es NP-difícil de encontrar. Un gráfico dirigido arbitrario también se puede transformar en un DAG, llamado su condensación, al contraer cada uno de sus componentes fuertemente conectados en un solo supervértice. Cuando el gráfico ya es acíclico, sus conjuntos de vértices de retroalimentación y arcos de retroalimentación más pequeños están vacíos, y su condensación es el gráfico mismo.
Cierre transitivo y reducción transitiva
El cierre transitivo de un DAG dado, con n vértices y m bordes, pueden construirse en el tiempo O(mn) por utilizando la búsqueda primero en amplitud o la búsqueda primero en profundidad para probar la accesibilidad desde cada vértice. Alternativamente, se puede resolver en el tiempo O(nω) donde ω < 2,373 es el exponente de los algoritmos de multiplicación de matrices; esta es una mejora teórica sobre el límite O(mn) para gráficos densos.
En todos estos algoritmos de cierre transitivo, es posible distinguir pares de vértices que son alcanzables por al menos un camino de longitud dos o más de pares que solo pueden conectarse por un camino de longitud uno. La reducción transitiva consiste en los bordes que forman caminos de longitud uno que son los únicos caminos que conectan sus puntos finales. Por lo tanto, la reducción transitiva se puede construir en los mismos límites de tiempo asintóticos que la clausura transitiva.
Problema de cierre
El problema de clausura toma como entrada un gráfico acíclico dirigido ponderado por vértice y busca el peso mínimo (o máximo) de una clausura: un conjunto de vértices C, de modo que ningún borde deje C. El problema puede formularse para grafos dirigidos sin el supuesto de aciclicidad, pero sin mayor generalidad, pues en este caso equivale al mismo problema sobre la condensación del grafo. Puede resolverse en tiempo polinomial usando una reducción al problema de flujo máximo.
Algoritmos de ruta
Algunos algoritmos se vuelven más simples cuando se usan en DAG en lugar de gráficos generales, según el principio de ordenamiento topológico. Por ejemplo, es posible encontrar las rutas más cortas y las rutas más largas desde un vértice de inicio dado en DAG en tiempo lineal procesando los vértices en un orden topológico y calculando la longitud de la ruta para cada vértice para que sea la longitud mínima o máxima obtenida a través de cualquier de sus bordes entrantes. Por el contrario, para gráficos arbitrarios, la ruta más corta puede requerir algoritmos más lentos, como el algoritmo de Dijkstra o el algoritmo de Bellman-Ford, y las rutas más largas en gráficos arbitrarios son NP-difíciles de encontrar.
Aplicaciones
Programación
Las representaciones gráficas acíclicas dirigidas de órdenes parciales tienen muchas aplicaciones en la programación de sistemas de tareas con restricciones de orden. Una clase importante de problemas de este tipo se relaciona con colecciones de objetos que deben actualizarse, como las celdas de una hoja de cálculo después de que se haya cambiado una de las celdas, o los archivos de objetos de una pieza de software de computadora después de que se haya cambiado su código fuente. cambió. En este contexto, un gráfico de dependencia es un gráfico que tiene un vértice para que cada objeto se actualice y un borde que conecta dos objetos cuando uno de ellos necesita actualizarse antes que el otro. Un ciclo en este gráfico se denomina dependencia circular y, por lo general, no se permite, porque no habría forma de programar de manera consistente las tareas involucradas en el ciclo. Los gráficos de dependencia sin dependencias circulares forman DAG.
Por ejemplo, cuando cambia una celda de una hoja de cálculo, es necesario volver a calcular los valores de otras celdas que dependen directa o indirectamente de la celda modificada. Para este problema, las tareas a programar son los recálculos de los valores de las celdas individuales de la hoja de cálculo. Las dependencias surgen cuando una expresión en una celda usa un valor de otra celda. En tal caso, el valor que se usa debe recalcularse antes que la expresión que lo usa. Ordenar topológicamente el gráfico de dependencia y usar este orden topológico para programar las actualizaciones de celdas permite que toda la hoja de cálculo se actualice con una sola evaluación por celda. Problemas similares de ordenación de tareas surgen en los archivos MAKE para la compilación de programas y la programación de instrucciones para la optimización de programas informáticos de bajo nivel.
La técnica de evaluación y revisión de programas (PERT), un método para la gestión de grandes proyectos humanos que fue una de las primeras aplicaciones de los DAG, utiliza una formulación algo diferente basada en DAG de las restricciones de programación. En este método, los vértices de un DAG representan hitos de un proyecto en lugar de tareas específicas a realizar. En cambio, una tarea o actividad está representada por un borde de un DAG, que conecta dos hitos que marcan el comienzo y la finalización de la tarea. Cada uno de esos bordes está etiquetado con una estimación de la cantidad de tiempo que le tomará a un equipo de trabajadores realizar la tarea. La ruta más larga en este DAG representa la ruta crítica del proyecto, la que controla el tiempo total del proyecto. Los hitos individuales se pueden programar de acuerdo con las longitudes de los caminos más largos que terminan en sus vértices.
Redes de procesamiento de datos
Se puede usar un gráfico acíclico dirigido para representar una red de elementos de procesamiento. En esta representación, los datos ingresan a un elemento de procesamiento a través de sus bordes de entrada y salen del elemento a través de sus bordes de salida.
Por ejemplo, en el diseño de circuitos electrónicos, los bloques lógicos combinacionales estáticos se pueden representar como un sistema acíclico de puertas lógicas que calcula una función de una entrada, donde la entrada y la salida de la función se representan como bits individuales. En general, la salida de estos bloques no se puede utilizar como entrada a menos que sea capturada por un registro o elemento de estado que mantenga sus propiedades acíclicas. Los esquemas de circuitos electrónicos, ya sea en papel o en una base de datos, son una forma de gráficos acíclicos dirigidos que utilizan instancias o componentes para formar una referencia dirigida a un componente de nivel inferior. Los circuitos electrónicos en sí mismos no son necesariamente acíclicos o dirigidos.
Los lenguajes de programación de flujo de datos describen sistemas de operaciones en flujos de datos y las conexiones entre las salidas de algunas operaciones y las entradas de otras. Estos lenguajes pueden ser convenientes para describir tareas repetitivas de procesamiento de datos, en las que la misma colección de operaciones conectadas de forma acíclica se aplica a muchos elementos de datos. Se pueden ejecutar como un algoritmo paralelo en el que cada operación se realiza mediante un proceso paralelo tan pronto como otro conjunto de entradas esté disponible para él.
En los compiladores, el código de línea recta (es decir, secuencias de sentencias sin bucles ni ramificaciones condicionales) se puede representar mediante un DAG que describe las entradas y salidas de cada una de las operaciones aritméticas realizadas dentro del código. Esta representación permite que el compilador realice la eliminación de subexpresiones comunes de manera eficiente. En un nivel más alto de organización de código, el principio de dependencias acíclicas establece que las dependencias entre módulos o componentes de un sistema de software grande deben formar un gráfico acíclico dirigido.
Las redes neuronales feedforward son otro ejemplo.
Estructuras causales
Los gráficos en los que los vértices representan eventos que ocurren en un tiempo definido, y donde los bordes siempre apuntan desde el vértice de tiempo temprano a un vértice de tiempo tardío del borde, son necesariamente dirigidos y acíclicos. La falta de un ciclo se debe a que el tiempo asociado con un vértice siempre aumenta a medida que sigue cualquier camino en el gráfico, por lo que nunca puede regresar a un vértice en un camino. Esto refleja nuestra intuición natural de que la causalidad significa que los eventos solo pueden afectar el futuro, nunca afectan el pasado y, por lo tanto, no tenemos bucles causales. Un ejemplo de este tipo de gráfico acíclico dirigido son los que se encuentran en el enfoque de conjunto causal de la gravedad cuántica, aunque en este caso los gráficos considerados son transitivamente completos. En el ejemplo del historial de versiones a continuación, cada versión del software está asociada con una hora única, generalmente la hora en que se guardó, comprometió o lanzó la versión. En los ejemplos de gráficos de citas a continuación, los documentos se publican a la vez y solo pueden hacer referencia a documentos más antiguos.
A veces, los eventos no están asociados con un tiempo físico específico. Siempre que los pares de eventos tengan una relación puramente causal, es decir, las aristas representan relaciones causales entre los eventos, tendremos un gráfico acíclico dirigido. Por ejemplo, una red bayesiana representa un sistema de eventos probabilísticos como vértices en un gráfico acíclico dirigido, en el que la probabilidad de un evento puede calcularse a partir de las probabilidades de sus predecesores en el DAG. En este contexto, el grafo moral de un DAG es el grafo no dirigido creado al agregar un borde (no dirigido) entre todos los padres del mismo vértice (a veces llamado casarse), y luego reemplazar todos los bordes dirigidos por no dirigidos. bordes Otro tipo de gráfico con una estructura causal similar es un diagrama de influencia, cuyos vértices representan decisiones a tomar o información desconocida, y cuyos bordes representan influencias causales de un vértice a otro. En epidemiología, por ejemplo, estos diagramas se utilizan a menudo para estimar el valor esperado de diferentes opciones de intervención.
Lo contrario también es cierto. Es decir, en cualquier aplicación representada por un gráfico acíclico dirigido, existe una estructura causal, ya sea un orden o tiempo explícito en el ejemplo o un orden que puede derivarse de la estructura del gráfico. Esto se debe a que todos los gráficos acíclicos dirigidos tienen un orden topológico, es decir, hay al menos una forma de poner los vértices en un orden tal que todos los bordes apunten en la misma dirección a lo largo de ese orden.
Historial de genealogía y versiones
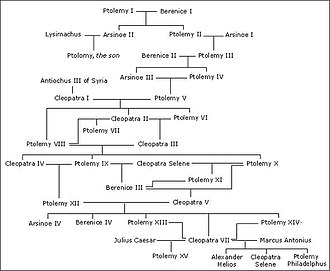
Los árboles genealógicos pueden verse como gráficos acíclicos dirigidos, con un vértice para cada miembro de la familia y un borde para cada relación padre-hijo. A pesar del nombre, estos gráficos no son necesariamente árboles debido a la posibilidad de matrimonios entre parientes (por lo que un niño tiene un ancestro común tanto del lado de la madre como del padre) causando el colapso del pedigrí. Los gráficos de descendencia matrilineal (relaciones madre-hija) y patrilineal (relaciones padre-hijo) son árboles dentro de este gráfico. Debido a que nadie puede convertirse en su propio antepasado, los árboles genealógicos son acíclicos.
El historial de versiones de un sistema de control de revisiones distribuido, como Git, generalmente tiene la estructura de un gráfico acíclico dirigido, en el que hay un vértice para cada revisión y un borde que conecta pares de revisiones que se derivaron directamente entre sí.. Estos no son árboles en general debido a fusiones.
En muchos algoritmos aleatorios de geometría computacional, el algoritmo mantiene un historial DAG que representa el historial de versiones de una estructura geométrica a lo largo de una secuencia de cambios en la estructura. Por ejemplo, en un algoritmo incremental aleatorizado para la triangulación de Delaunay, la triangulación cambia al reemplazar un triángulo por tres triángulos más pequeños cuando se agrega cada punto, y al "voltear" operaciones que reemplazan pares de triángulos por un par diferente de triángulos. El DAG de historial para este algoritmo tiene un vértice para cada triángulo construido como parte del algoritmo y los bordes de cada triángulo a los otros dos o tres triángulos que lo reemplazan. Esta estructura permite que las consultas de ubicación de puntos se respondan de manera eficiente: para encontrar la ubicación de un punto de consulta q en la triangulación de Delaunay, siga un ruta en el historial DAG, en cada paso moviéndose al triángulo de reemplazo que contiene q. El último triángulo alcanzado en este camino debe ser el triángulo de Delaunay que contiene q.
Gráficos de citas
En un gráfico de citas los vértices son documentos con una única fecha de publicación. Los bordes representan las citas de la bibliografía de un documento a otros documentos necesariamente anteriores. El ejemplo clásico proviene de las citas entre artículos académicos, como se señala en el artículo de 1965 "Networks of Scientific Papers" por Derek J. de Solla Price, quien luego produjo el primer modelo de una red de citas, el modelo Price. En este caso, el recuento de citas de un artículo es solo el grado de entrada del vértice correspondiente de la red de citas. Esta es una medida importante en el análisis de citas. Las sentencias de los tribunales brindan otro ejemplo, ya que los jueces respaldan sus conclusiones en un caso al recordar otras decisiones anteriores tomadas en casos anteriores. Un ejemplo final lo proporcionan las patentes que deben hacer referencia al estado de la técnica anterior, patentes anteriores que son relevantes para la reivindicación de patente actual. Teniendo en cuenta las propiedades especiales de los gráficos acíclicos dirigidos, se pueden analizar las redes de citas con técnicas que no están disponibles cuando se analizan los gráficos generales considerados en muchos estudios que utilizan el análisis de redes. Por ejemplo, la reducción transitiva brinda nuevos conocimientos sobre las distribuciones de citas que se encuentran en diferentes aplicaciones, destacando diferencias claras en los mecanismos que crean redes de citas en diferentes contextos. Otra técnica es el análisis de ruta principal, que rastrea los enlaces de citas y sugiere las cadenas de citas más significativas en un gráfico de citas determinado.
El modelo Price es demasiado simple para ser un modelo realista de una red de citación, pero es lo suficientemente simple para permitir soluciones analíticas para algunas de sus propiedades. Muchos de ellos se pueden encontrar utilizando resultados derivados de la versión no dirigida del modelo Price, el modelo Barabási–Albert. Sin embargo, dado que el modelo de Price da un gráfico acíclico dirigido, es un modelo útil al buscar cálculos analíticos de propiedades únicas a gráficos acíclicos dirigidos. Por ejemplo, la longitud del camino más largo, desde el nodo n-th añadido a la red al primer nodo en la red, escalas como In ()n){displaystyle ln(n)}.
Compresión de datos
Los gráficos acíclicos dirigidos también se pueden usar como una representación compacta de una colección de secuencias. En este tipo de aplicación, uno encuentra un DAG en el que los caminos forman las secuencias dadas. Cuando muchas de las secuencias comparten las mismas subsecuencias, estas subsecuencias compartidas se pueden representar mediante una parte compartida del DAG, lo que permite que la representación use menos espacio del que se necesitaría para enumerar todas las secuencias por separado. Por ejemplo, el gráfico de palabras acíclicas dirigidas es una estructura de datos en informática formada por un gráfico acíclico dirigido con una sola fuente y con bordes etiquetados por letras o símbolos; las rutas desde el origen hasta los sumideros en este gráfico representan un conjunto de cadenas, como palabras en inglés. Cualquier conjunto de secuencias se puede representar como caminos en un árbol, formando un vértice de árbol para cada prefijo de una secuencia y haciendo que el padre de uno de estos vértices represente la secuencia con un elemento menos; el árbol formado de esta manera para un conjunto de cuerdas se llama trie. Un gráfico de palabras acíclicas dirigidas ahorra espacio en un trie al permitir que las rutas diverjan y se vuelvan a unir, de modo que un conjunto de palabras con los mismos sufijos posibles se puede representar mediante un solo vértice de árbol.
La misma idea de usar un DAG para representar una familia de rutas ocurre en el diagrama de decisión binario, una estructura de datos basada en DAG para representar funciones binarias. En un diagrama de decisión binario, cada vértice que no es sumidero se etiqueta con el nombre de una variable binaria, y cada sumidero y cada arista se etiquetan con un 0 o un 1. El valor de la función para cualquier asignación de verdad a las variables es el valor en el sumidero encontrado siguiendo una ruta, comenzando desde el vértice de origen único, que en cada vértice no sumidero sigue el borde saliente etiquetado con el valor de la variable de ese vértice. Así como los gráficos de palabras acíclicas dirigidas se pueden ver como una forma comprimida de intentos, los diagramas de decisión binarios se pueden ver como formas comprimidas de árboles de decisión que ahorran espacio al permitir que las rutas se vuelvan a unir cuando concuerdan en los resultados de todas las decisiones restantes.
Contenido relacionado
Historia de la inteligencia artificial (IA)
Transparencia referencial
Producto directo