Gradiente

ImprimirCitar

Derivados multivariados (matemáticos)

El gradiente, representado por las flechas azules, denota la dirección del mayor cambio de una función de escalar. Los valores de la función están representados en escala gris y aumentan el valor de blanco (bajo) a oscuro (alto).

En el cálculo vectorial, el gradiente de una función diferenciable de valor escalar $f$ de varias variables es el campo vectorial (o función valorada por vectores) $nabla f$ cuyo valor en un punto $p$ es la "dirección y tasa de aumento más rápido". Si el gradiente de una función no es cero en un punto $p$ , la dirección del gradiente es la dirección en la que la función aumenta más rápidamente desde $p$ , y la magnitud del gradiente es la tasa de aumento en esa dirección, el mayor derivado direccional absoluto. Además, un punto donde el gradiente es el vector cero se conoce como un punto estacionario. El gradiente juega así un papel fundamental en la teoría de la optimización, donde se utiliza para maximizar una función por ascensión gradiente. En términos libres de coordenadas, el gradiente de una función ${displaystyle f({bf {{r})}}}$ puede definirse por:

{displaystyle df=nabla fcdot d{bf {r}}}

Donde df es el cambio infinitesimal total en f para un desplazamiento infinitesimal ${displaystyle d{bf {r}}}$ , y se ve que es maximal cuando ${displaystyle d{bf {r}}}$ está en la dirección del gradiente $nabla f$ . El símbolo nabla $nabla$ , escrito como un triángulo boca abajo y pronunciado "del", denota el operador diferencial vectorial.

Cuando se utiliza un sistema de coordenadas en el que los vectores base no son funciones de posición, el gradiente es dado por el vector cuyos componentes son los derivados parciales de $f$ a $p$ . Es decir, ${displaystyle fcolon mathbb {R} ^{n}to mathbb {R} }$ , su gradiente ${displaystyle nabla fcolon mathbb {R} ^{n}to mathbb {R} ^{n}}$ se define en el punto ${displaystyle p=(x_{1},ldotsx_{n})}$ dentro No...espacio dimensional como vector

{displaystyle nabla f(p)={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)\vdots \{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}.}

El gradiente es dual al derivado total $df$ : el valor del gradiente en un punto es un vector tangente – un vector en cada punto; mientras que el valor del derivado en un punto es un vector cotangente – un funcional lineal en vectores. Están relacionados en que el producto de punto del gradiente de $f$ en un momento $p$ con otro vector tangente $v$ iguala el derivado direccional de $f$ a $p$ de la función $v$ ; es decir, ${textstyle nabla f(p)cdot mathbf {v} ={frac {partial f}{partial mathbf {v} }}(p)=df_{p}(mathbf {v})}$ . El gradiente admite múltiples generalizaciones a funciones más generales en los manifolds; véase § Generalizaciones.

Motivación

Gradiente de la función 2D

f () x, Sí.) xe - x 2 + Sí. 2)

se trama como flechas azules sobre la parcela pseudocolor de la función.

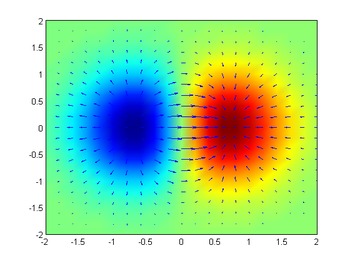
Considere una habitación donde la temperatura viene dada por un campo escalar, $T$ , por lo que en cada punto $(x, y, z)$ la temperatura es $T (x, y, z)$ , independiente del tiempo. En cada punto de la habitación, el gradiente de $T$ en ese punto mostrará la dirección en la que la temperatura sube más rápidamente, alejándose de $(x, y, z)$ . La magnitud del gradiente determinará qué tan rápido sube la temperatura en esa dirección.

Considere una superficie cuya altura sobre el nivel del mar en el punto $(x, y)$ es $H (x, y)$ . El gradiente de $H$ en un punto es un vector plano que apunta en la dirección de la pendiente o pendiente más empinada en ese punto. La inclinación de la pendiente en ese punto viene dada por la magnitud del vector gradiente.

El gradiente también se puede usar para medir cómo cambia un campo escalar en otras direcciones, en lugar de solo en la dirección del mayor cambio, tomando un producto escalar. Suponga que la pendiente más empinada de una colina es del 40%. Un camino que va directamente cuesta arriba tiene una pendiente del 40%, pero un camino que va alrededor de la colina en ángulo tendrá una pendiente menor. Por ejemplo, si la carretera forma un ángulo de 60° desde la dirección cuesta arriba (cuando ambas direcciones se proyectan en el plano horizontal), la pendiente a lo largo de la carretera será el producto escalar entre el vector de gradiente y un vector unitario a lo largo de la carretera., es decir, 40% por el coseno de 60°, o 20%.

Más generalmente, si la función de altura de la colina $H$ es diferenciable, entonces el gradiente de $H$ punteado con un vector unitario da la pendiente de la colina en la dirección del vector, la derivada direccional de $H$ a lo largo del vector unitario.

Notación

El gradiente de una función $f$ punto $a$ generalmente escrito como ${displaystyle nabla f(a)}$ . También puede ser denotado por cualquiera de los siguientes:

${displaystyle {vec {nabla }}f(a)}$ : enfatizar la naturaleza vectorial del resultado.
$grad f$
${displaystyle partial _{i}f}$ y $f_{i}$ : Nota de Einstein.

Definición

El gradiente de la función

f () x, Sí.) = - 2 x + porque 2 Sí.) 2

representado como un campo vectorial proyectado en el plano inferior.

El gradiente (o campo vectorial de gradiente) de una función escalar $f (x 1, x 2, x 3, \dots, x n)$ se denota $\nabla f$ o $\nabla \to f$ donde $\nabla$ (nabla) denota el operador diferencial vectorial, del. La notación $grad f$ también se usa comúnmente para representar el gradiente. El gradiente de $f$ se define como el campo vectorial único cuyo producto escalar con cualquier vector $v$ en cada punto $x$ es la derivada direccional de $f$ a lo largo de $v$ . Es decir,

{displaystyle {big (}nabla f(x){big)}cdot mathbf {v} =D_{mathbf {v} }f(x)}

donde la mano del lado derecho es la derivada direccional y hay muchas formas de representarla. Formalmente, la derivada es dual al gradiente; ver relación con la derivada.

Cuando una función también depende de un parámetro como el tiempo, el gradiente a menudo se refiere simplemente al vector de sus derivadas espaciales únicamente (consulte Gradiente espacial).

La magnitud y la dirección del vector de gradiente son independientes de la representación de coordenadas particular.

Coordenadas cartesianas

En el sistema de coordenadas cartesianas tridimensional con métrica euclidiana, el gradiente, si existe, viene dado por:

{displaystyle nabla f={frac {partial f}{partial x}}mathbf {i} +{frac {partial f}{partial y}}mathbf {j} +{frac {partial f}{partial z}}mathbf {k}}

donde $i$ , $j$ , $k$ son los vectores unitarios estándar en las direcciones de $x$ , $y$ y $z$ coordenadas, respectivamente. Por ejemplo, el gradiente de la función

{displaystyle f(x,y,z)=2x+3y^{2}-sin(z)}

{displaystyle nabla f=2mathbf {i} +6ymathbf {j} -cos(z)mathbf {k}.}

En algunas aplicaciones, se acostumbra representar el gradiente como un vector de fila o un vector de columna de sus componentes en un sistema de coordenadas rectangulares; este artículo sigue la convención de que el gradiente es un vector columna, mientras que la derivada es un vector fila.

Coordenadas cilíndricas y esféricas

En coordenadas cilíndricas con métrica euclidiana, el gradiente viene dado por:

{displaystyle nabla f(rhovarphiz)={frac {partial f}{partial rho }}mathbf {e} _{rho }+{frac {1}{rho }}{frac {partial f}{partial varphi }}mathbf {e} _{varphi }+{frac {partial f}{partial z}}mathbf {e} _{z},}

donde $ρ$ es la distancia axial, $φ$ es el acimutal o ángulo acimutal, $z$ es la coordenada axial, y $e <sub ρ$ , $e φ$ y $e z$ son vectores unitarios que apuntan a lo largo de las direcciones de las coordenadas.

En coordenadas esféricas, el gradiente viene dado por:

{displaystyle nabla f(r,thetavarphi)={frac {partial f}{partial r}}mathbf {e} _{r}+{frac {1}{r}}{frac {partial f}{partial theta }}mathbf {e} _{theta }+{frac {1}{rsin theta }}{frac {partial f}{partial varphi }}mathbf {e} _{varphi },}

donde $r$ es la distancia radial, $φ$ es el ángulo azimutal y $θ$ es el ángulo polar, y $e r$ , $e θ$ y $e φ$ son nuevamente vectores unitarios locales que apuntan en las direcciones de coordenadas (es decir, la base covariante normalizada).

Para el gradiente en otros sistemas de coordenadas ortogonales, consulte Coordenadas ortogonales (operadores diferenciales en tres dimensiones).

Coordenadas generales

Consideramos coordenadas generales, que escribimos como $x 1, \dots, x i, \dots, x n$ , donde $n$ es el número de dimensiones del dominio. Aquí, el índice superior se refiere a la posición en la lista de la coordenada o componente, por lo que $x 2$ se refiere a la segundo componente, no la cantidad $x$ al cuadrado. La variable de índice $i$ se refiere a un elemento arbitrario $x yo$ . Usando la notación de Einstein, el gradiente se puede escribir como:

{displaystyle nabla f={frac {partial f}{partial x^{i}}}g^{ij}mathbf {e} _{j}}

{textstyle mathrm {d} f={frac {partial f}{partial x^{i}}}mathbf {e} ^{i}}

Donde ${displaystyle mathbf {e} _{i}=partial mathbf {x} /partial x^{i}}$ y ${displaystyle mathbf {e} ^{i}=mathrm {d} x^{i}}$ referencia a las bases covariantes y contravariantes locales no normalizadas respectivamente, $g^{ij}$ es el tensor métrico inverso, y la convención de la sumación de Einstein implica la suma sobre i y j.

Si las coordenadas son ortogonales podemos expresar fácilmente el gradiente (y el diferencial) en términos de las bases normalizadas, a las que nos referimos como ${hat {mathbf {e} }}_{i}$ y ${displaystyle {hat {mathbf {e} }}^{i}}$ , utilizando los factores de escala (también conocidos como coeficientes Lamé) ${displaystyle h_{i}=lVert mathbf {e} _{i}rVert ={sqrt {g_{ii}}}=1,/lVert mathbf {e} ^{i}rVert }$ :

{displaystyle nabla f={frac {partial f}{partial x^{i}}}g^{ij}{hat {mathbf {e} }}_{j}{sqrt {g_{jj}}}=sum _{i=1}^{n},{frac {partial f}{partial x^{i}}}{frac {1}{h_{i}}}mathbf {hat {e}} _{i}}

{textstyle mathrm {d} f=sum _{i=1}^{n},{frac {partial f}{partial x^{i}}}{frac {1}{h_{i}}}mathbf {hat {e}} ^{i}}

donde no podemos usar la notación de Einstein, ya que es imposible evitar la repetición de más de dos índices. A pesar del uso de índices superiores e inferiores, ${displaystyle mathbf {hat {e}} _{i}}$ , ${displaystyle mathbf {hat {e}} ^{i}}$ , y $h_{i}$ no son contravariantes ni covariantes.

La última expresión se evalúa como las expresiones anteriores para coordenadas cilíndricas y esféricas.

Relación con la derivada

Relación con la derivada total

El gradiente está estrechamente relacionado con el derivado total (diferencial total) $df$ : son transpose (dual) entre sí. Uso de la convención que vectores en $mathbb {R} ^{n}$ son representados por vectores de columna, y que covectores (mapas lineales ${displaystyle mathbb {R} ^{n}to mathbb {R} }$ ) están representados por vectores de fila, el gradiente $nabla f$ y el derivado $df$ se expresan como vector de columna y fila, respectivamente, con los mismos componentes, pero transpose entre sí:

{displaystyle nabla f(p)={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)\vdots \{frac {partial f}{partial x_{n}}}(p)end{bmatrix}};}

{displaystyle df_{p}={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)&cdots &{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}.}

Si bien ambos tienen los mismos componentes, difieren en qué tipo de objeto matemático representan: en cada punto, el derivado es un vector cotangente, una forma lineal (covector) que expresa cuánto el (scalar) cambio de salida para un determinado cambio infinitesimal en (vector) entrada, mientras que en cada punto, el gradiente es un vector tangente, que representa un cambio infinitesimal en (vector) entrada. En símbolos, el gradiente es un elemento del espacio tangente en un punto, ${displaystyle nabla f(p)in T_{p}mathbb {R} ^{n}}$ , mientras que el derivado es un mapa del espacio tangente a los números reales, ${displaystyle df_{p}colon T_{p}mathbb {R} ^{n}to mathbb {R} }$ . Los espacios tangentes en cada punto $mathbb {R} ^{n}$ puede ser "naturalmente" identificado con el espacio vectorial $mathbb {R} ^{n}$ en sí mismo, y similarmente el espacio cotangente en cada punto puede ser identificado naturalmente con el espacio vectorial dual ${displaystyle (mathbb {R} ^{n})^{*}}$ de los covectores; así el valor del gradiente en un punto se puede pensar en un vector en el original $mathbb {R} ^{n}$ No sólo como un vector tangente.

Desde el punto de vista computacional, dado un vector tangente, el vector se puede multiplicar por la derivada (como matrices), que es igual a tomar el producto escalar con el gradiente:

{displaystyle (df_{p})(v)={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)&cdots &{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}{begin{bmatrix}v_{1}\vdots \v_{n}end{bmatrix}}=sum _{i=1}^{n}{frac {partial f}{partial x_{i}}}(p)v_{i}={begin{bmatrix}{frac {partial f}{partial x_{1}}}(p)\vdots \{frac {partial f}{partial x_{n}}}(p)end{bmatrix}}cdot {begin{bmatrix}v_{1}\vdots \v_{n}end{bmatrix}}=nabla f(p)cdot v}

Derivada diferencial o (exterior)

La mejor aproximación lineal a una función diferenciable

{displaystyle fcolon mathbb {R} ^{n}to mathbb {R} }

en un punto $x$ en $R n$ es un mapa lineal de $R n$ a $R$ que a menudo se denota por $df x$ o $Df (x)$ y llamó la derivada diferencial o total de $f$ en $x$ . La función $df$ , que asigna $x$ a $df x$ , se denomina diferencial total o derivada exterior de $f$ y es un ejemplo de una forma diferencial de 1.

Al igual que la derivada de una función de una sola variable representa la pendiente de la tangente a la gráfica de la función, la derivada direccional de una función en varias variables representa la pendiente del hiperplano tangente en la dirección del vector.

El gradiente está relacionado con el diferencial por la fórmula

{displaystyle (nabla f)_{x}cdot v=df_{x}(v)}

para cualquier $v ▪ R n$ , donde $cdot$ es el producto de punto: tomar el producto de punto de un vector con el gradiente es el mismo que tomar el derivado direccional a lo largo del vector.

Si $R n$ se ve como el espacio de (dimensión $n$ ) vectores de columna (de números reales), entonces uno puede considerar $df$ como el vector fila con componentes

{displaystyle left({frac {partial f}{partial x_{1}}},dots{frac {partial f}{partial x_{n}}}right),}

para que $df x (v)$ viene dada por la multiplicación de matrices. Asumiendo la métrica euclidiana estándar en $R n$ , el gradiente es entonces el vector de columna correspondiente, es decir,

{displaystyle (nabla f)_{i}=df_{i}^{mathsf {T}}.}

Aproximación lineal a una función

La mejor aproximación lineal a una función se puede expresar en términos del gradiente, en lugar de la derivada. El gradiente de una función $f$ del espacio euclidiano $R n$ a $R$ en cualquier punto en particular $x 0$ en $R n$ caracteriza la mejor aproximación lineal a $f$ en $x 0$ . La aproximación es la siguiente:

{displaystyle f(x)approx f(x_{0})+(nabla f)_{x_{0}}cdot (x-x_{0})}

para $x$ cerca de $x 0$ , donde $(\nabla f) x 0$ es el gradiente de $f$ calculado en $x 0$ , y el punto denota el producto escalar en $R n$ . Esta ecuación es equivalente a los dos primeros términos en la expansión de la serie de Taylor multivariable de $f$ en $x 0$ .

Relación con el derivado de Fréchet

Sea $U$ un conjunto abierto en $R n$ . Si la función $f : U \to R$ es derivable, entonces la diferencial de $f$ es la derivada Fréchet de $f$ . Así $\nabla f$ es una función de $U$ al espacio $R n$ tal que

{displaystyle lim _{hto 0}{frac {|f(x+h)-f(x)-nabla f(x)cdot h|}{|h|}}=0,}

Como consecuencia, las propiedades habituales de la derivada se mantienen para el gradiente, aunque el gradiente no es una derivada en sí misma, sino dual a la derivada:

Linearity: El gradiente es lineal en el sentido de que si $f$ y $g$ son dos funciones de valor real diferenciables en el punto $a ▪ R n$ , y $α$ y $β$ son dos constantes, entonces $αf + βg$ es diferente en $a$ , y más ${displaystyle nabla left(alpha f+beta gright)(a)=alpha nabla f(a)+beta nabla g(a).}$
Regla de producto: Si $f$ y $g$ son funciones de valor real diferenciables en un punto $a ▪ R n$ , entonces la regla del producto afirma que el producto $fg$ es diferente en $a$ , y ${displaystyle nabla (fg)(a)=f(a)nabla g(a)+g(a)nabla f(a).}$
Regla de cadena: Supongamos que $f : A \to R$ es una función de valor real definida en un subconjunto $A$ de $R n$ , y eso $f$ es diferente en un punto $a$ . Hay dos formas de la regla de la cadena que se aplican al gradiente. Primero, supongamos que la función $g$ es una curva paramétrica; es decir, una función $g : I \to R n$ mapas a subset $I \subset R$ en $R n$ . Si $g$ es diferente en un punto $c ▪ I$ tales que $g () c) a$ , entonces ${displaystyle (fcirc g)'(c)=nabla f(a)cdot g'(c),}$ donde ∘ es el operador de composición: $() f \circ g) x) f () g () x)$ .

Más generalmente, si en cambio $I \subset R k$ , entonces se cumple lo siguiente:

{displaystyle nabla (fcirc g)(c)={big (}Dg(c){big)}^{mathsf {T}}{big (}nabla f(a){big)},}

() Dg)

Para la segunda forma de la regla de la cadena, suponga que $h : I \to R$ es una función de valor real en un subconjunto $I$ de $R$ , y que $h$ es diferenciable en el punto $f (a) \in I$ . Después

{displaystyle nabla (hcirc f)(a)=h'{big (}f(a){big)}nabla f(a).}

Más propiedades y aplicaciones

Conjuntos de niveles

Una superficie de nivel, o isosuperficie, es el conjunto de todos los puntos donde alguna función tiene un valor dado.

Si $f$ es diferenciable, entonces el producto escalar $(\nabla f) x \cdot v$ del gradiente en un punto $x$ con un vector $v$ da la derivada direccional de $f$ en $x$ en la dirección $v$ . De ello se deduce que en este caso el gradiente de $f$ es ortogonal a los conjuntos de niveles de $f$ . Por ejemplo, una superficie nivelada en un espacio tridimensional se define mediante una ecuación de la forma $F (x, y, z) = c$ . El gradiente de $F$ es entonces normal a la superficie.

De manera más general, cualquier hipersuperficie incrustada en una variedad de Riemann se puede cortar mediante una ecuación de la forma $F (P) = 0$ tal que $dF$ no es cero en ninguna parte. El gradiente de $F$ es entonces normal a la hipersuperficie.

Del mismo modo, una hipersuperficie algebraica afín puede definirse mediante una ecuación $F (x 1,..., x n) = 0$ , donde $F$ es un polinomio. El gradiente de $F$ es cero en un punto singular de la hipersuperficie (esta es la definición de un punto singular). En un punto no singular, es un vector normal distinto de cero.

Campos vectoriales conservativos y el teorema del gradiente

El gradiente de una función se llama campo de gradiente. Un campo de gradiente (continuo) es siempre un campo vectorial conservativo: su integral de línea a lo largo de cualquier camino depende solo de los puntos finales del camino y puede evaluarse mediante el teorema del gradiente (el teorema fundamental del cálculo para integrales de línea). Por el contrario, un campo vectorial conservativo (continuo) es siempre el gradiente de una función.

Generalizaciones

Jacobiano

La matriz jacobiana es la generalización del gradiente para funciones vectoriales de varias variables y aplicaciones diferenciables entre espacios euclidianos o, más generalmente, variedades. Otra generalización para una función entre espacios de Banach es la derivada de Fréchet.

Suppose $f : R n \to R m$ es una función tal que cada uno de sus derivados parciales de primer orden existen en $R n$ . Entonces la matriz Jacobiana $f$ se define como un $m \times n$ matriz, denotada por ${displaystyle mathbf {J} _{mathbb {f} }(mathbb {x})}$ o simplemente $mathbf {J}$ . El $() i, j)$ la entrada ${displaystyle mathbf {J} _{ij}={frac {partial f_{i}}{partial x_{j}}}}$ . Explícitamente

{displaystyle mathbf {J} ={begin{bmatrix}{dfrac {partial mathbf {f} }{partial x_{1}}}&cdots &{dfrac {partial mathbf {f} }{partial x_{n}}}end{bmatrix}}={begin{bmatrix}nabla ^{mathsf {T}}f_{1}\vdots \nabla ^{mathsf {T}}f_{m}end{bmatrix}}={begin{bmatrix}{dfrac {partial f_{1}}{partial x_{1}}}&cdots &{dfrac {partial f_{1}}{partial x_{n}}}\vdots &ddots &vdots \{dfrac {partial f_{m}}{partial x_{1}}}&cdots &{dfrac {partial f_{m}}{partial x_{n}}}end{bmatrix}}.}

Gradiente de un campo vectorial

Dado que la derivada total de un campo vectorial es un mapeo lineal de vectores a vectores, es una cantidad tensorial.

En coordenadas rectangulares, el gradiente de un campo vectorial $f = (f 1, f 2, f 3)$ está definido por:

{displaystyle nabla mathbf {f} =g^{jk}{frac {partial f^{i}}{partial x^{j}}}mathbf {e} _{i}otimes mathbf {e} _{k},}

(donde se usa la notación de suma de Einstein y el producto tensorial de los vectores $e i$ y $e k$ es un tensor diádico de tipo (2,0)). En general, esta expresión es igual a la transpuesta de la matriz jacobiana:

{displaystyle {frac {partial f^{i}}{partial x^{j}}}={frac {partial (f^{1},f^{2},f^{3})}{partial (x^{1},x^{2},x^{3})}}.}

En coordenadas curvilíneas, o más generalmente en una variedad curva, el gradiente involucra símbolos de Christoffel:

{displaystyle nabla mathbf {f} =g^{jk}left({frac {partial f^{i}}{partial x^{j}}}+{Gamma ^{i}}_{jl}f^{l}right)mathbf {e} _{i}otimes mathbf {e} _{k},}

donde $g jk$ son los componentes del tensor métrico inverso y el $e i$ son los vectores base de coordenadas.

Expresado de manera más invariable, el gradiente de un campo vectorial $f$ puede definirse mediante la conexión de Levi-Civita y el tensor métrico:

{displaystyle nabla ^{a}f^{b}=g^{ac}nabla _{c}f^{b},}

donde $\nabla c$ es la conexión.

Variedades de Riemann

Para cualquier función suave $f$ en una variedad Riemanniana $(M, g)$ , el gradiente de $f$ es el campo vectorial $\nabla f$ tal que para cualquier campo vectorial $X$ ,

{displaystyle g(nabla f,X)=partial _{X}f,}

es decir,

{displaystyle g_{x}{big (}(nabla f)_{x},X_{x}{big)}=(partial _{X}f)(x),}

donde $g x ()$ denota el producto interno de vectores tangentes en $x$ definido por la métrica $g$ y $\partial X f$ es la función que toma cualquier punto $x \in M$ a la derivada direccional de $f$ en la dirección $X$ , evaluado en $x$ . En otras palabras, en un gráfico de coordenadas $φ$ de un subconjunto abierto de $M$ a un subconjunto abierto de $R n$ , $(\partial X f)(x)$ viene dado por:

{displaystyle sum _{j=1}^{n}X^{j}{big (}varphi (x){big)}{frac {partial }{partial x_{j}}}(fcirc varphi ^{-1}){Bigg |}_{varphi (x)},}

donde $X j$ denota el $j$ ésimo componente de $X$ en este gráfico de coordenadas.

Entonces, la forma local del gradiente toma la forma:

{displaystyle nabla f=g^{ik}{frac {partial f}{partial x^{k}}}{textbf {e}}_{i}.}

Generalizando el caso $M = R n$ , el gradiente de una función está relacionado con su derivada exterior, ya que

{displaystyle (partial _{X}f)(x)=(df)_{x}(X_{x}).}

Más precisamente, el gradiente $\nabla f$ es el campo vectorial asociado al diferencial de 1 forma $df$ usando el isomorfismo musical

sharp =sharp ^{g}colon T^{*}Mto TM

(llamado "agudo") definido por la métrica $g$ . La relación entre la derivada exterior y el gradiente de una función en $R n$ es una caso especial de este en el que la métrica es la métrica plana dada por el producto escalar.

Contenido relacionado

Más resultados...