Geometría descriptiva

El mismo objeto de seis lados, en proyección isométrica

geometría descriptiva es la rama de la geometría que permite la representación de objetos tridimensionales en dos dimensiones mediante el uso de un conjunto específico de procedimientos. Las técnicas resultantes son importantes para la ingeniería, la arquitectura, el diseño y el arte. La base teórica de la geometría descriptiva la proporcionan las proyecciones geométricas planas. La primera publicación conocida sobre esta técnica fue "Underweysung der Messung mit dem Zirckel und Richtscheyt" (Observación de la medición con el compás y el nivel de burbuja), publicado en Linien, Nuremberg: 1525, por Alberto Durero. El arquitecto italiano Guarino Guarini también fue un pionero de la geometría proyectiva y descriptiva, como se desprende de su Placita Philosophica (1665), Euclides Adauctus (1671) y Architettura Civile. (1686; no se publicó hasta 1737), anticipándose al trabajo de Gaspard Monge (1746-1818), a quien generalmente se le atribuye la invención de la geometría descriptiva. A Gaspard Monge se le suele considerar el "padre de la geometría descriptiva" debido a sus avances en la resolución de problemas geométricos. Sus primeros descubrimientos se produjeron en 1765 mientras trabajaba como dibujante de fortificaciones militares, aunque sus hallazgos se publicaron más tarde.

Los protocolos de Monge permiten dibujar un objeto imaginario de forma que pueda modelarse en tres dimensiones. Todos los aspectos geométricos del objeto imaginario se tienen en cuenta en tamaño/escala y forma reales, y se pueden visualizar como se ve desde cualquier posición en el espacio. Todas las imágenes están representadas en una superficie bidimensional.

La geometría descriptiva utiliza la técnica de creación de imágenes de proyectores imaginarios paralelos que emanan de un objeto imaginario y que intersectan un plano imaginario de proyección en ángulos rectos. Los puntos acumulativos de intersecciones crean la imagen deseada.

Protocolos

• Proyecto dos imágenes de un objeto en direcciones perpendiculares y arbitrarias mutuamente. Cada vista de imagen alberga tres dimensiones del espacio, dos dimensiones que se muestran como ejes a gran escala, mutuamente perpendiculares y uno como un eje invisible (vista de punto) recediendo en el espacio de imagen (en profundidad). Cada una de las dos vistas adyacentes de la imagen comparte una vista a gran escala de una de las tres dimensiones del espacio.
• Cualquiera de estas imágenes puede servir como punto de partida para una tercera vista proyectada. La tercera vista puede comenzar una cuarta proyección, y en ad infinitum. Estas proyecciones secuenciales representan cada una un giro circular, 90° en el espacio para ver el objeto desde una dirección diferente.
• Cada nueva proyección utiliza una dimensión a toda escala que aparece como dimensión de punto de vista en la vista anterior. Para lograr la visión a gran escala de esta dimensión y darle cabida dentro de la nueva visión, es necesario que se ignore la visión anterior y se proceda a la segunda vista anterior en la que esta dimensión aparece a gran escala.
• Cada nueva vista se puede crear proyectando en cualquiera de un número infinito de direcciones, perpendicular a la dirección anterior de proyección. (Vea las muchas direcciones de los radios de una rueda de carro cada perpendicular a la dirección del eje.) El resultado es uno de paso indirectamente sobre un objeto en giros de 90° y viendo el objeto de cada paso. Cada nueva vista se añade como una vista adicional a una pantalla de diseño de proyección ortográfico y aparece en un "desplegamiento del modelo de caja de vidrio".

Además de las seis vistas principales estándar ortográficas (Frente; Lado derecho; Lado izquierdo; Arriba; Abajo; Trasera), la geometría descriptiva se esfuerza por producir cuatro vistas de solución básicas: la longitud real de una línea (es decir, tamaño completo, no en escorzo), la vista puntual (vista final) de una línea, la forma verdadera de un plano (es decir, tamaño completo a escala, o no en escorzo) y la vista de borde de un plano (es decir, vista de un plano con el línea de visión perpendicular a la línea de visión asociada con la línea de visión para producir la verdadera forma de un avión). A menudo sirven para determinar la dirección de proyección para la vista siguiente. Mediante el proceso de paso tortuoso de 90°, proyectar en cualquier dirección desde el punto de vista de una línea produce su verdadera vista de longitud; proyectar en una dirección paralela a una vista de línea de longitud real produce su vista de punto, proyectar la vista de punto de cualquier línea en un plano produce la vista de borde del plano; proyectar en una dirección perpendicular a la vista del borde de un plano producirá la vista de la forma real (a escala). Se puede recurrir a estos diversos puntos de vista para ayudar a resolver problemas de ingeniería planteados por los principios de la geometría sólida.

Heurística

El estudio de la geometría descriptiva tiene un valor heurístico. Promueve la visualización y las capacidades analíticas espaciales, así como la capacidad intuitiva de reconocer la dirección de visión para presentar mejor un problema geométrico para su solución. Ejemplos representativos:

La mejor dirección para ver

• Dos líneas de costura (pipes, tal vez) en posiciones generales para determinar la ubicación de su conector más corto (común perpendicular)
• Dos líneas de sierra (pipes) en posiciones generales tales que su conector más corto se ve a toda escala
• Dos líneas de costura en posiciones generales como el conector más corto paralelo a un plano dado se ve a toda escala (por ejemplo, para determinar la posición y la dimensión del conector más corto a una distancia constante de una superficie radiante)
• Una superficie plana de tal manera que un agujero perforado perpendicular se ve a toda escala, como si mirara a través del agujero (por ejemplo, para probar las autorizaciones con otros agujeros perforados)
• Un avión equidistante de dos líneas en posiciones generales (por ejemplo, para confirmar la distancia segura de radiación?)
• La distancia más corta de un punto a un plano (por ejemplo, para localizar la posición más económica para sujetar)
• La línea de intersección entre dos superficies, incluyendo superficies curvas (por ejemplo, para el tamaño más económico de las secciones?)
• El verdadero tamaño del ángulo entre dos planos

Aún no se ha adoptado un estándar para presentar vistas de modelado por computadora análogas a las proyecciones ortográficas secuenciales. En las ilustraciones siguientes se presenta un candidato para ello. Las imágenes de las ilustraciones se crearon utilizando gráficos por computadora de ingeniería tridimensionales.

El modelado tridimensional por computadora produce un espacio virtual "detrás del tubo", por así decirlo, y puede producir cualquier vista de un modelo desde cualquier dirección dentro de este espacio virtual. Lo hace sin necesidad de vistas ortográficas adyacentes y, por lo tanto, puede parecer que vuelve obsoleto el tortuoso protocolo escalonado de la Geometría Descriptiva. Sin embargo, dado que la geometría descriptiva es la ciencia de la obtención de imágenes legítimas o permitidas de un espacio tridimensional o más, en un plano, es un estudio indispensable para mejorar las posibilidades de modelado por computadora.

Ejemplos

Encontrar el conector más corto entre dos líneas oblicuas PR y SU dadas

Dadas las coordenadas X, Y y Z de P, R, S y U, las proyecciones 1 y 2 se dibujan a escala en los planos X-Y y X-Z, respectivamente.

Para obtener una vista real (la longitud en la proyección es igual a la longitud en el espacio 3D) de una de las líneas: SU en este ejemplo, la proyección 3 se dibuja con la línea bisagra H_2,3 paralelo a S₂U₂. Para obtener una vista frontal de SU, la proyección 4 se dibuja con la línea de articulación H_3,4 perpendicular a S₃U₃. La distancia perpendicular d da la distancia más corta entre PR y SU.

Para obtener los puntos Q y T en estas líneas que den esta distancia más corta, la proyección 5 se dibuja con la línea bisagra H_4,5 paralela a P₄R ₄, lo que hace que P₅R₅ y S₅U₅ sean vistas verdaderas (cualquier proyección de una vista final es una vista verdadera). Proyectar la intersección de estas líneas, Q₅ y T₅ de nuevo a la proyección 1 (líneas magenta y etiquetas) permite leer sus coordenadas en los ejes X, Y y Z..

Soluciones generales

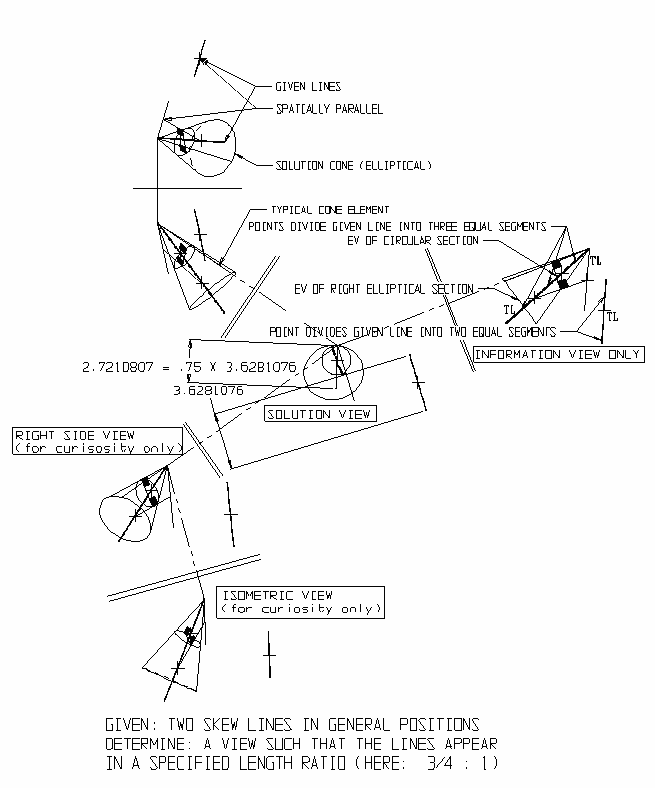
Las soluciones generales son una clase de soluciones dentro de la geometría descriptiva que contienen todas las soluciones posibles a un problema. La solución general está representada por un único objeto tridimensional, generalmente un cono, cuyas direcciones de elementos son la dirección de visión (proyección) deseada para cualquiera de un número infinito de vistas de solución.

Por ejemplo: para encontrar la solución general tal que aparezcan dos líneas oblicuas de longitud desigual en posiciones generales (por ejemplo, ¿cohetes en vuelo?):

• Longitud igual
• Longitud igual y paralelo
• Longitud igual y perpendicular (por ejemplo, para el objetivo ideal de al menos uno)
• Igual a longitudes de una relación especificada
• otros.

En los ejemplos, la solución general para cada solución característica deseada es un cono, cada elemento del cual produce una de un número infinito de vistas de solución. Cuando se desean dos o más características, digamos de las enumeradas anteriormente, (y para las cuales existe una solución), proyectar en la dirección de cualquiera de los dos elementos de intersección (un elemento, si los conos son tangentes) entre los dos conos produce las características deseadas. vista de solución. Si los conos no se cruzan no existe solución. Los ejemplos siguientes están anotados para mostrar los principios geométricos descriptivos utilizados en las soluciones. TL = longitud verdadera; EV = Vista de borde.

Higos. 1-3 a continuación demuestran (1) geometría descriptiva, soluciones generales y (2) simultáneamente, un estándar potencial para presentar dichas soluciones en formatos de diseño ortográfico, de vista múltiple.

El estándar potencial emplea dos vistas ortográficas estándar adyacentes (aquí, Frontal y Superior) con una "línea de plegado" entre. Como no hay necesidad posterior de “dar un paso tortuoso”; 90° alrededor del objeto, en secuencias estándar de dos pasos para llegar a una vista de solución (es posible ir directamente a la vista de solución), este protocolo más corto se tiene en cuenta en el diseño. Cuando el protocolo de un paso reemplaza al protocolo de dos pasos, el protocolo de "doble plegado" Se utilizan líneas. En otras palabras, cuando uno cruza las líneas dobles no está dando un giro tortuoso de 90° sino un giro no ortodireccional directamente a la vista de la solución. Como la mayoría de los paquetes de gráficos por computadora de ingeniería generan automáticamente las seis vistas principales del modelo de caja de vidrio, así como una vista isométrica, estas vistas a veces se agregan por curiosidad heurística.

Figura 1: Geometría descriptiva - líneas de costura que aparecen perpendicular

Figura 2: Geometría descriptiva - líneas de sierra aparecen igual longitud

Figura 3: Geometría descriptiva - las líneas de junta aparecen en la relación de longitud especificada