Geometría del taxi

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Tipo de geometría métrica

Puntos en tres círculos (el conjunto de puntos equidistantes desde un punto dado) en geometría de taxicab

A geometría de taxis o a Geometría de Manhattan es una geometría cuya función de distancia habitual o métrica de la geometría euclidiana es reemplazada por una nueva métrica en la que la distancia entre dos puntos es la suma de las diferencias absolutas de sus coordenadas cartesianas. La métrica de taxi también se conoce como distancia rectilínea, L₁ distancia, L¹ distancia o $ell _{1}$ norm (ver espacio Lp), distancia de serpiente, distancia de manzana, distancia de Manhattan o longitud de Manhattan. Estos últimos nombres se refieren al trazado rectilineal en la isla de Manhattan, donde el camino más corto que un taxi viaja entre dos puntos es la suma de los valores absolutos de distancias que viaja en las avenidas y en las calles.

La geometría se ha utilizado en el análisis de regresión desde el siglo XVIII y a menudo se la denomina LASSO. La interpretación geométrica data de la geometría no euclidiana del siglo XIX y se debe a Hermann Minkowski.

In ${displaystyle mathbb {R} ^{2}}$ , la distancia de taxi entre dos puntos $(x_{1},y_{1})$ y $(x_{2},y_{2})$ es ${displaystyle left|x_{1}-x_{2}right|+left|y_{1}-y_{2}right|}$ . Es decir, es la suma de los valores absolutos de las diferencias en ambas coordenadas.

Definición formal

La distancia del taxi, ${displaystyle d_{text{T}}}$ , entre dos vectores ${displaystyle mathbf {p} =(p_{1},p_{2},dotsp_{n}){text{ and }}mathbf {q} =(q_{1},q_{2},dotsq_{n})}$ en una n-dimensional espacio vectorial real con sistema de coordenadas cartesiano fijo, es la suma de las longitudes de las proyecciones del segmento de línea entre los puntos sobre los ejes de coordenadas. Más formalmente,

{displaystyle d_{text{T}}(mathbf {p}mathbf {q})=left|mathbf {p} -mathbf {q} right|_{text{T}}=sum _{i=1}^{n}left|p_{i}-q_{i}right|}

{displaystyle mathbb {R} ^{2}}

{displaystyle mathbf {p} =(p_{1},p_{2})}

{displaystyle mathbf {q} =(q_{1},q_{2})}

{displaystyle left|p_{1}-q_{1}right|+left|p_{2}-q_{2}right|.}

Historia

La métrica L¹ fue utilizada en el análisis de regresión en 1757 por Roger Joseph Boscovich. La interpretación geométrica se remonta a finales del siglo XIX y al desarrollo de geometrías no euclidianas, en particular por Hermann Minkowski y su desigualdad de Minkowski, de la cual esta geometría es un caso especial, particularmente utilizada en la geometría de números (Minkowski 1910). La formalización de los espacios Lp se atribuye a (Riesz 1910).

Propiedades

La distancia del taxi depende de la rotación del sistema de coordenadas, pero no depende de su reflexión sobre un eje de coordenadas o su traslación. La geometría del taxi satisface todos los axiomas de Hilbert (una formalización de la geometría euclidiana) excepto el axioma lado-ángulo-lado, ya que dos triángulos con lados igualmente "largos" Dos lados y un ángulo idéntico entre ellos normalmente no son congruentes a menos que los lados mencionados sean paralelos.

Bolas

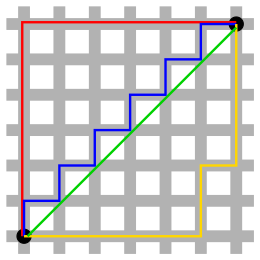
Una bola topológica es un conjunto de puntos con una distancia fija, llamada la radio, desde un punto llamado centro. In n-dimensional Geometría euclidiana, las bolas son esferas. En la geometría de taxicab, la distancia se determina por una métrica diferente que en la geometría euclidiana, y la forma de la bola también cambia. In n dimensiones, una bola de taxi está en forma de una n- ortodoxo dimensional. En dos dimensiones, son cuadrados con lados orientados a un ángulo de 45° a los ejes de coordenadas. La imagen a la derecha muestra por qué es verdad, mostrando en rojo el conjunto de todos los puntos con una distancia fija de un centro, mostrado en azul. A medida que el tamaño de los bloques de la ciudad disminuye, los puntos se vuelven más numerosos y se convierten en un cuadrado girado en una geometría de taxi continuo. Mientras que cada lado tendría longitud $sqrt{2}r$ usando una métrica euclidiana, donde r es el radio del círculo, su longitud en la geometría del taxi es 2r. Así, la circunferencia de un círculo es 8r. Así, el valor de un análogo geométrico a $pi$ 4 en esta geometría. La fórmula para el círculo de unidad en la geometría de taxis es $|x|+|y|=1$ en coordenadas cartesianas y

{displaystyle r={frac {1}{left|sin theta right|+left|cos theta right|}}}

Un círculo de radio 1 (usando esta distancia) es la vecindad de von Neumann de su centro.

Un círculo de radio r para la distancia de Chebyshev (L∞ métrica) en un plano también es un cuadrado con una longitud de lado 2r paralelo a los ejes de coordenadas, por lo que La distancia plana de Chebyshev se puede ver como equivalente mediante rotación y escala a la distancia plana de taxi. Sin embargo, esta equivalencia entre las métricas L₁ y L_∞ no se generaliza a dimensiones superiores.

Siempre que cada par en una colección de estos círculos tenga una intersección no vacía, existe un punto de intersección para toda la colección; por tanto, la distancia de Manhattan forma un espacio métrico inyectivo.

Longitud del arco

Vamos $y=f(x)$ ser una función continuamente diferenciable en $mathbb {R} ^{2}$ . Vamos $s$ ser la longitud del arco del taxi de la curva del planar definida por $f$ en algún intervalo ${displaystyle [a,b]}$ . Luego la longitud del taxi $i^{text{th}}$ partición regular infinitesimal del arco, ${displaystyle Delta s_{i}}$ , se da por:

${displaystyle Delta s_{i}=Delta x_{i}+Delta y_{i}=Delta x_{i}+|f(x_{i})-f(x_{i-1})|}$

Por el teorema de valor medio, existe algún punto $x_{i}^{*}$ entre $x_{i}$ y ${displaystyle x_{i-1}}$ tales que ${displaystyle f(x_{i})-f(x_{i-1})=f'(x_{i}^{*})dx_{i}}$ .

${displaystyle Delta s_{i}=Delta x_{i}+|f'(x_{i}^{*})|Delta x_{i}=Delta x_{i}(1+|f'(x_{i}^{*})|)}$

Entonces... $s$ se da como la suma de cada partición de $s$ on $[a,b]$ como son arbitrariamente pequeños.

${displaystyle {begin{aligned}s&=lim _{nrightarrow infty }sum _{i=1}^{n}Delta x_{i}(1+|f'(x_{i}^{*})|)\&=int _{a}^{b}1+|f'(x)|,dxend{aligned}}}$

Para probar esto, tome el círculo de taxicab de radio $r$ centrado en el origen. Su curva en el primer cuadrante es dada por ${displaystyle f(x)=-x+r}$ cuya longitud es

${displaystyle s=int _{0}^{r}1+|-1|dx=2r}$

Multiplicando este valor ${displaystyle 4}$ to account for the remaining quadrants gives ${displaystyle 8r}$ , que está de acuerdo con la circunferencia de un círculo de taxis. Ahora tome el círculo euclidiano del radio $r$ centrado en el origen, que es dado por ${displaystyle f(x)={sqrt {r^{2}-x^{2}}}}$ . Su longitud de arco en el primer cuadrante es dada por

${displaystyle {begin{aligned}s&=int _{0}^{r}1+|{frac {-x}{sqrt {r^{2}-x^{2}}}}|dx\&=x+{sqrt {r^{2}-x^{2}}}{bigg |}_{0}^{r}\&=r-(-r)\&=2rend{aligned}}}$

Contabilidad de los quadrantes restantes ${displaystyle 4times 2r=8r}$ otra vez. Por lo tanto, la circunferencia del círculo de taxis y el círculo euclidiano en la métrica de taxis son iguales. De hecho, para cualquier función $f$ que es monotónico y diferenciable con un derivado continuo sobre un intervalo $[a,b]$ , la longitud del arco $f$ sobre $[a,b]$ es ${displaystyle (b-a)+mid f(b)-f(a)mid }$ .

Dos triángulos isoceles derecha taxicab. Tres ángulos y dos piernas son congruentes, pero los triángulos no son congruentes. Por lo tanto, ASASA no es un teorema de congruencia en la geometría de taxi.

Congruencia de triángulos

Dos triángulos son congruentes si y sólo si tres lados correspondientes tienen la misma distancia y tres ángulos correspondientes tienen la misma medida. Hay varios teoremas que garantizan la congruencia de triángulos en la geometría euclidiana, a saber, Ángulo-Ángulo-Lado (AAS), Ángulo-Lado-Ángulo (ASA), Lado-Ángulo-Lado (SAS) y Lado-Lado-Lado (SSS). Sin embargo, en la geometría de los taxis, sólo SASAS garantiza la congruencia de triángulos.

Tomemos, por ejemplo, dos triángulos rectángulos de taxi isósceles cuyos ángulos miden 45-90-45. Los dos catetos de ambos triángulos tienen longitud de taxi 2, pero las hipotenusas no son congruentes. Este contraejemplo elimina AAS, ASA y SAS. También elimina AASS, AAAS e incluso ASASA. Tener tres ángulos congruentes y dos lados no garantiza la congruencia de triángulos en la geometría de un taxi. Por lo tanto, el único teorema de congruencia de triángulos en geometría de taxis es SASAS, donde los tres lados correspondientes deben ser congruentes y al menos dos ángulos correspondientes deben ser congruentes. Este resultado se debe principalmente al hecho de que la longitud de un segmento de recta depende de su orientación en la geometría del taxi.

Aplicaciones

Detección comprimida

En la solución de un sistema subdeterminado de ecuaciones lineales, el término de regularización para el vector del parámetro se expresa en términos del $ell _{1}$ norma (geometría de taxicab) del vector. Este enfoque aparece en el marco de recuperación de señales llamado detección comprimida.

Diferencias de distribuciones de frecuencia

La geometría del taxi se puede utilizar para evaluar las diferencias en distribuciones de frecuencia discretas. Por ejemplo, en el empalme de ARN, las distribuciones posicionales de los hexámeros, que trazan la probabilidad de que cada hexámero aparezca en cada nucleótido dado cerca de un sitio de empalme, se pueden comparar con la distancia L1. Cada distribución de posición se puede representar como un vector donde cada entrada representa la probabilidad de que el hexámero comience en un determinado nucleótido. Una distancia L1 grande entre los dos vectores indica una diferencia significativa en la naturaleza de las distribuciones, mientras que una distancia pequeña denota distribuciones con formas similares. Esto equivale a medir el área entre las dos curvas de distribución porque el área de cada segmento es la diferencia absoluta entre las dos curvas. probabilidades en ese punto. Cuando se suma para todos los segmentos, proporciona la misma medida que la distancia L1.