Geodésicas de Schwarzschild

En la relatividad general, Schwarzschild geodesics describir el movimiento de partículas de prueba en el campo gravitacional de una masa fija central M,{textstyle M,} es decir, movimiento en la métrica Schwarzschild. La geodésica Schwarzschild ha sido fundamental en la validación de la teoría de Einstein de la relatividad general. Por ejemplo, proporcionan predicciones precisas de la precesión anómala de los planetas en el Sistema Solar y de la deflexión de la luz por gravedad.

La geodésica Schwarzschild sólo se refiere al movimiento de partículas de masas tan pequeñas que contribuyen poco al campo gravitacional. Sin embargo, son muy exactos en muchos escenarios astrofísicos siempre que m{textstyle m} es mucho más pequeño que la masa central M{textstyle M}Por ejemplo, para planetas orbitando su estrella. La geodésica Schwarzschild es también una buena aproximación al movimiento relativo de dos cuerpos de masa arbitraria, siempre que la masa Schwarzschild M{textstyle M} es igual a la suma de las dos masas individuales m1{fnMicrosoftstyle m_{1} y m2{textstyle m_{2}. Esto es importante para predecir el movimiento de estrellas binarias en la relatividad general.

Contexto histórico

La métrica de Schwarzschild recibe su nombre en honor a su descubridor Karl Schwarzschild, quien encontró la solución en 1915, sólo aproximadamente un mes después de la publicación de la teoría de la relatividad general de Einstein. Fue la primera solución exacta de las ecuaciones de campo de Einstein además de la solución trivial del espacio plano.

En 1931, Yusuke Hagihara publicó un artículo que mostraba que la trayectoria de una partícula de prueba en la métrica de Schwarzschild se puede expresar en términos de funciones elípticas.

Samuil Kaplan en 1949 ha demostrado que existe un radio mínimo para que la órbita circular sea estable en la métrica de Schwarzschild.

Métrica de Schwarzschild

Una solución exacta a las ecuaciones de campo de Einstein es la métrica Schwarzschild, que corresponde al campo gravitacional externo de un cuerpo de masa sin carga, no rotativo, esféricamente simétrico M{textstyle M}. La solución Schwarzschild se puede escribir como

c2dτ τ 2=()1− − rsr)c2dt2− − dr21− − rsr− − r2dSilencio Silencio 2− − r2pecado2⁡ ⁡ Silencio Silencio dφ φ 2{displaystyle C^{2}{dtau ¿Por qué? {fnK} {fnMicroc {fnK}} {f}} {f}} {f} {2}dtheta ^{2}-r^{2}sin ^{2}theta,dvarphi ^{2}

Donde

τ τ {displaystyle tau }, en el caso de una partícula de prueba de masa positiva pequeña, es el tiempo adecuado (tiempo medido por un reloj que se mueve con la partícula) en segundos,

c{displaystyle c} es la velocidad de la luz en metros por segundo,

t{displaystyle t} es, r_{text{s}}}" xmlns="http://www.w3.org/1998/Math/MathML">r■rs{displaystyle r confíar_{text{s}}r_{text{s}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c9fc3420fc0caf8350f7083bf5c5906f12a4bab4" style="vertical-align: -0.671ex; width:6.076ex; height:2.176ex;"/>, la coordinación del tiempo (tiempo medido por un reloj estacionario en el infinito) en segundos,

r{displaystyle r} es, r_{text{s}}}" xmlns="http://www.w3.org/1998/Math/MathML">r■rs{displaystyle r confíar_{text{s}}r_{text{s}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c9fc3420fc0caf8350f7083bf5c5906f12a4bab4" style="vertical-align: -0.671ex; width:6.076ex; height:2.176ex;"/>, la coordinación radial (circunferencia de un círculo centrado en la estrella dividida por 2π π {displaystyle 2pi}) en metros,

Silencio Silencio {displaystyle theta } es la colatitud (ángulo del norte) en los radians,

φ φ {displaystyle varphi } es la longitud en radians, y

rs{displaystyle r_{text{s}} es el radio Schwarzschild del cuerpo masivo (en metros), que está relacionado con su masa M{textstyle M} por

rs=2GMc2,{displaystyle r_{text{}={frac {2GM}{c^{2}}}}}

Donde G{textstyle G} es la constante gravitacional. La teoría clásica de la gravedad Newtoniana se recupera en el límite como la relación rsr{fnMicroc} {fnK}} {fnK}}} {fn}}}}} {f}}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}} {f}}}}}} {}}}}}}}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} va a cero. En ese límite, la métrica vuelve a la definida por la relatividad especial.

En la práctica, esta proporción es casi siempre extremadamente pequeña. Por ejemplo, el radio Schwarzschild rs{textstyle r_{text{s}}} de la Tierra es aproximadamente 9 mm (3.8pulgada); en la superficie de la Tierra, las correcciones a la gravedad Newtoniana son sólo una parte en mil millones. El radio Schwarzschild del Sol es mucho más grande, aproximadamente 2953 metros, pero en su superficie, la relación rsr{fnMicroc} {fnK}} {fnK}}} {fn}}}}} {f}}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}} {f}}}}}} {}}}}}}}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} es aproximadamente 4 partes en un millón. Una estrella enana blanca es mucho más densa, pero incluso aquí la proporción en su superficie es aproximadamente 250 partes en un millón. La relación sólo se hace grande cerca de objetos ultra-denses como estrellas de neutrones (donde la proporción es aproximadamente 50%) y agujeros negros.

Órbitas de partículas de prueba

Podemos simplificar el problema utilizando la simetría para eliminar una variable de consideración. Ya que la métrica Schwarzschild es simétrica Silencio Silencio =π π 2{textstyle theta ={frac {cHFF} } {2}}, cualquier geodésico que comience a moverse en ese plano permanecerá indefinidamente en ese plano (el plano es totalmente geodésico). Por lo tanto, orientamos el sistema de coordenadas para que la órbita de la partícula se encuentra en ese plano, y fijar el Silencio Silencio {textstyle theta } coordinación para π π 2{fnMicroc} {cHFF} } {2}} para que la métrica (de este plano) simplifica

c2dτ τ 2=()1− − rsr)c2dt2− − dr21− − rsr− − r2dφ φ 2.{displaystyle c^{2}dtau ¿Qué? {fnK} {fnMicroc {fnh} {fnh}} {fnh} {f}}} {2}dvarphi} ^{2}.

Dos constantes de movimiento (valores que no cambian con el tiempo adecuado τ τ {displaystyle tau }) se puede identificar (cf. la derivación dada a continuación). Una es la energía total E{textstyle E}:

()1− − rsr)dtdτ τ =Emc2.{displaystyle left(1-{frac {text{s}}{r}right){frac {dt}{dtau }={frac {E} {mc^{2}}}

y el otro es el momento angular específico:

h=Lμ μ =r2dφ φ dτ τ,{displaystyle h={frac {L}{mu} - ¿Qué?

Donde L{textstyle L} es el impulso angular total de los dos cuerpos, y μ μ {textstyle mu } es la masa reducida. Cuando M≫ ≫ m{fnMicrosoftstyle Mgg m}, la masa reducida es aproximadamente igual a m{textstyle m}. A veces se supone que m=μ μ {textstyle m=mu}. En el caso del planeta Mercurio esta simplificación introduce un error más del doble que el efecto relativista. Al discutir geodésica, m{textstyle m} puede ser considerado ficticio, y lo que importa son las constantes Em{fnMicroc} {E} {m}} y h{textstyle h}. Para cubrir toda la geodésica posible, necesitamos considerar casos en los que Em{fnMicroc} {E} {m}} es infinita (dar trayectorias de fotones) o imaginario (para geodésica taquiónica). Para el caso fotonico, también necesitamos especificar un número correspondiente a la relación de las dos constantes, es decir, mhE{fnMicroc} {mh} {E}}, que puede ser cero o un número real no cero.

Sustituyendo estas constantes en la definición de la métrica de Schwarzschild

c2=()1− − rsr)c2()dtdτ τ)2− − 11− − rsr()drdτ τ)2− − r2()dφ φ dτ τ)2,{displaystyle {fnMicrosoft Sans Serif}

produce una ecuación de movimiento para el radio como una función del tiempo adecuado τ τ {textstyle tau }:

()drdτ τ)2=E2m2c2− − ()1− − rsr)()c2+h2r2).{displaystyle left {frac}{dtau }right)}{2}={frac {E^{2}}{m^{2} {2}}}}}-left(1-{frac} {m} {m}{2}}}} {i}} {i}}}}left(1-{frac}={frac}}}}}={f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { {fnMicrosoft Sans Serif} {h^{2} {r^{2}}derecha).}

La solución formal a esto es

τ τ =∫ ∫ dr± ± E2m2c2− − ()1− − rsr)()c2+h2r2).{displaystyle tau =int {fnMicroc {}{pm {fnMicroc} {E^{2} {m^{2}c^{2}}-left(1-{frac} {fnMicrosoft Sans Serif} Sí.

Tenga en cuenta que la raíz cuadrada será imaginaria para las geodésicas taquiónicas.

Usando la relación superior entre dtdτ τ {fnMicroc} {dt}{dtau } y E{textstyle E}, también podemos escribir

t=∫ ∫ dr± ± c()1− − rsr)1− − ()1− − rsr)()c2+h2r2)m2c2E2.{displaystyle t=int {frac}{pm cleft(1-{frac {frac {text{s}}}}right){sqrt {1-left(1-{frac {text{s}}right)left(c^{2}+{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} - Sí.

Puesto que asintomáticamente el integrado es inversamente proporcional a r− − rs{textstyle r-r_{text{s}}, esto muestra que en r,Silencio Silencio,φ φ,t{textstyle r,thetavarphit} marco de referencia si r{textstyle r} enfoques rs{textstyle r_{text{s}}} lo hace de manera exponencial sin llegar a ella. Sin embargo, como función τ τ {textstyle tau }, r{textstyle r} no alcanza rs{textstyle r_{text{s}}}.

Las soluciones anteriores son válidas mientras el integrando sea finito, pero una solución total puede involucrar dos o una infinidad de piezas, cada una descrita por la integral pero con signos alternos para la raíz cuadrada.

Cuando E=mc2{textstyle E=mc^{2} y h=0{textstyle h=0}, podemos resolver para t{textstyle t} y τ τ {textstyle tau } explícitamente:

t=constante± ± rsc()23()rrs)32+2rrs+In⁡ ⁡ Silenciorrs− − 1Silenciorrs+1)τ τ =constante± ± 23rsc()rrs)32{displaystyle {begin{aligned}t limit={text{constant}pm {fnMicroc {fnMicroc} {fnMicroc} {fnMicroc}} {fnMicroc} {fnMicroc}} {fnMicroc}}} {fnMicroc} {f} {fnMicroc}} {fnMicroc} {f}}}}}}}}}}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnMift {fn}fn}fn}f}f}f}fn}fnMift {fnMift {m}fnMift {fn}f}fnMift {fn}f}fn}fn}fn}fnMiff}f}fn}}fnMiff}}f}fn {2}}left ({frac {r}{text{s}}}right)}{frac} {frac} {f}}}}}}derecho)} {3}{2}+2{sqrt {frac} {} {fn}} {fn}}}fn} {fnMicroc {fnMicroc {fnh}}} {fnMicroc}}} {fnMicroc {f}}}}}} {fnMicroc {f}}}}}}}+1}derecha)tauau {texto {constant}pm {fnMicroc {2} {fnMicroc} {fnMicroc}}c}left({frac} {fnMicroc}} {f}} {fnK} {fnK}} {f}}}} {f} {f}fnK}}}f}} {f}f}} {f}f}f}}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}fnKfnfnf}f}f}f}f}f}f}fn {fnMicrosoft Sans Serif} {3} {2}end{aligned}}

y para la geodésica fotonicam=0{textstyle m=0}) con cero impulso angular

t=constante± ± 1c()r+rsIn⁡ ⁡ Silenciorrs− − 1Silencio)τ τ =constante.{displaystyle {begin{aligned}t ventaja={text{constant}pm {frac {1}{c}}left(r+r_{text{}ln}lnc} left sometida{frac {r} {r_{text{s}}}} {justo en la vidaderecha)tau ################################################################################################################################################################################################################################################################

(Aunque el tiempo adecuado es trivial en el caso fotonico, se puede definir un parámetro affine λ λ {textstyle lambda }, y luego la solución a la ecuación geodésica es r=c1λ λ +c2{fnMicrosoftstyle r=c_{1}lambda +c_{2})

Otro caso solvable es el en el que E=0{textstyle E=0} y t{textstyle t} y φ φ {textstyle varphi } son constantes. En el volumen donde <math alttext="{textstyle rrc)rs{textstyle r mader_{text{s}}<img alt="{textstyle r esto da para el tiempo adecuado

τ τ =constante± ± rsc()arcsin⁡ ⁡ rrs− − rrs()1− − rrs)).{displaystyle tau ={text{constant}pm {fnMicroc {fnMicrosoft} {fnMicrosoft {fnMicrosoft}} {fnMicrosoft} {fnMicrosoft}}} {fnMicrosoft {fnMicrosoft {fn}}}}} {fnMicroc {f}fnMicroc}} {f}}}f}}}}f}f}f}fn}f}fn}fnMicrocf}fn}f}fn}f}fn}fn}fn}fn}fn}fn}fn}fn}fnMift {fnMift {fnMicrocsin}fn}}fnMift {fn}fn}fn}fn}fn}fnMicrocsin}fn}fn}fn}fn}fn {fnMicroc} {fn} {fnh}}}} {fnMic {fnh}}}}left(1-{frac {r} {r_{text{s}}}right)}right).}

Esto está cerca de soluciones con E2m2{fnMicroc} {}} {fn}} {fn}}} {fn}}}} {fn}}}} {fn}}}}}}}}}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}} pequeño y positivo. Fuera de rs{textstyle r_{text{s}}} el E=0{textstyle E=0} la solución es taquiónica y el "tiempo apropiado" es el espacio-como:

τ τ =constante± ± irsc()In⁡ ⁡ ()rrs+rrs− − 1)+rrs()rrs− − 1)).{displaystyle tau ={text{constant}pm {fnfnfnfnh}c}lnlnleft({sqrt {frac}}c}c}c}left(lnlnleft {sqrt {sqrt {fnh} {fnfnhfnh}}}}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}cccccccccccccccccccccccccccccccccccncccccccccccccc {} {fn}} {fnMicrosoft}}} {fnMicrosoft}}}} {fn}}}}}} {fn}} {fn}}} {fn}}}} {fn}}}}}}}}} {\\fnH00}}}}}}}}}}}}}} {\ {fnMicroc {fnMicroc {fnMicroc}}}}}}}left({frac} {r} {r_{text{s}}}}}derecha)}}}}} {derecho)}

Esto está cerca de otras soluciones taquiónicas E2m2{fnMicroc} {}} {fn}} {fn}}} {fn}}}} {fn}}}} {fn}}}}}}}}}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}} pequeño y negativo. La constante t{textstyle t} geodésico táquico fuera rs{textstyle r_{text{s}}} no es continuado por una constante t{textstyle t} geodésica dentro rs{textstyle r_{text{s}}}, pero más bien continúa en una "región exterior paralela" (ver coordenadas Kruskal–Szekeres). Otras soluciones taquiónicas pueden entrar en un agujero negro y volver a salir a la región exterior paralela. La constante t{textstyle t} solución dentro del horizonte del evento (rs{textstyle r_{text{s}}}) continúa por una constante t{textstyle t} solución en un agujero blanco.

Cuando el impulso angular no es cero podemos reemplazar la dependencia del tiempo apropiado por una dependencia del ángulo φ φ {textstyle varphi } utilizando la definición de h{textstyle h}

()drdφ φ)2=()drdτ τ)2()dτ τ dφ φ)2=()drdτ τ)2()r2h)2,{displaystyle left({frac {dr}{dvarphi Bien. Bien. Bien. ¿Qué?

que produce la ecuación de la órbita

()drdφ φ)2=r4b2− − ()1− − rsr)()r4a2+r2){displaystyle left {frac {dvarphi }}right)^{2}={frac {4}{b^{2}}}}-left(1-{frac {frac}} {b}} {b}}}} Está bien. {fnK} {fnMicrosoft Sans Serif}

donde, por brevedad, dos escalas de longitud, a{textstyle a} y b{textstyle b}, han sido definidos por

a=hc,b=cLE=hmcE.{displaystyle {begin{aligned}a ventaja={frac {h}{c},b {CL} {E}={frac} {hmc} {E}}.end{aligned}}

Tenga en cuenta que en el caso taquiónico, a{textstyle a} será imaginario y b{textstyle b} real o infinito.

La misma ecuación también se puede derivar usando un enfoque lagrangiano o la ecuación Hamilton-Jacobi (ver abajo). La solución de la ecuación de la órbita es

φ φ =∫ ∫ dr± ± r21b2− − ()1− − rsr)()1a2+1r2).{displaystyle varphi =int {fnMicroc {fnMicrosoft}{pm {fnK}}-left(1-{frac} Está bien. {1}}}}}}}}}}} {fnMicroc {1}}}}}}}}}}}}} {f}} {fn0}}} {fnMicroc}}}}}}} {f}}}}}}}} {f}}}} {f}}}}}} {f}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

Esto se puede expresar en términos de la función elíptica Weierstrass ℘ ℘ {textstyle wp}.

Velocidades locales y retardadas

A diferencia de la mecánica clásica, en las coordenadas Schwarzschild drdτ τ {fnMicroc} {fnh}rm} {fnh}rm} {cH00}rm} {cH00} {cH00} {cH00} {cH00}} {cH00} {cH00} {cH00}. y rdφ φ dτ τ {fnMicroc} {fnh}varphi } {fn} {fn} {fn}} {fn}} {fn}}} {fn}}}}} {fn}}}} {fn}}}}}}}}}} {fn}}}}}}}}} {} {}}}}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}} {}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} no son el radial v∥ ∥ {textstyle v_{parallel} y transversales v⊥ ⊥ {textstyle v_{perp} componentes de la velocidad local v{textstyle v} (en relación con un observador estacionario), en su lugar dan los componentes para la celeridad que están relacionados con v{textstyle v} por

drdτ τ =v∥ ∥ 1− − rsrγ γ {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\\fnMicrosoft\\\\\\\\\\fnMicrom\\\\\fnMicrom\\\\\\\\\\\\\\\\\\\\\\\\\fnMin {}r}r{rm} {d}tau }=v_{parallel {fnMicroc {fnMicroc} {fnMicrosoft}}}}f}} gamma

para el radial y

dφ φ dτ τ =v⊥ ⊥ rγ γ {fnMicroc {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\\fnMicrosoft\\\\\\fnMicrom\\\\\\\\fnMicrom\\\\\\\\\\\\\\\\\\\\\\\\\\ {d}varphi } {{rm {d}tau }={frac {v_{perp } {r} gamma }

para el componente transversal del movimiento, con v2=v∥ ∥ 2+v⊥ ⊥ 2{textstyle v^{2}=v_{parallel }{2}+v_{perp } {2}. El contable de coordenadas lejos de la escena observa la velocidad retardada por shapiro v^ ^ {textstyle {hat {}}}, que se da por la relación

v^ ^ ⊥ ⊥ =v⊥ ⊥ 1− − rsr{displaystyle {hat {fnK}_{p} }=v_{perp }{sqrt {1-{frac {}}}} y v^ ^ ∥ ∥ =v∥ ∥ ()1− − rsr){displaystyle {hat {}_{parallel ¿Por qué?.

El factor de dilatación de tiempo entre el contador y la partícula de prueba móvil también se puede poner en la forma

dτ τ dt=1− − rsrγ γ {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\\fnMicrosoft\\\\\\\\\\fnMicrom\\\\\fnMicrom\\\\\\\\\\\\\\\\\\\\\\\\\fnMin {d}tau. {d}t}={frac} {fnMicroc {fnMicroc} {fnMicrosoft}} {fnMicrosoft}} {f}}} {fnMicroc}}}} {f}}}} {f}}}} {fnf}}}}} {f}}} {fnKf}}}}}}}}}}} { }

donde el numerador es la gravedad, y el denominador es el componente cinemático de la dilatación del tiempo. Para una partícula que cae de la infinidad el factor izquierdo es igual al factor derecho, ya que la velocidad en caída v{textstyle v} coincide con la velocidad de escape crsr{fnMicroc} {fnK}}} {f}}}} {fn}}}} {f}}}}}}}}} {}}} {}}}} {}}}}}} {}}}} {}}}}}} {}}}}} {}}}}}}} {}}}}} {}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} en este caso.

Las dos constantes del impulso angular L{textstyle L} y energía total E{textstyle E} de una partícula de prueba con masa m{textstyle m} en términos de v{textstyle v}

L=mv⊥ ⊥ rγ γ {displaystyle L=m v_{perp } rgamma }

y

E=mc21− − rsrγ γ {displaystyle E=mc^{2} {sqrt {1-{frac {f}} {}}}}}}}} gamma

dónde

E=Erest+Ekin+Epot{displaystyle E=E_{rm}+E_{rm} {kin}+E_{rm {pot}}

y

Erest=mc2,Ekin=()γ γ − − 1)mc2,Epot=()1− − rsr− − 1)γ γ mc2{displaystyle E_{rm}=mc^{2} E_{rm {kin}=(gamma -1)mc^{2} {fnMicrosoft Sans Serif} {fnMicroc {fnMicroc {fnh}} {}}}}}}}}}} {derecho)} {2}

Para las partículas de prueba masivas γ γ {textstyle gamma } es el factor Lorentz γ γ =1/1− − v2/c2{textstyle gamma =1/{sqrt {1-v^{2}/c^{2}}} y τ τ {textstyle tau } es el momento adecuado, mientras que para partículas sin masa como fotones γ γ {textstyle gamma } se establece 1{fnMicrosoftstyle 1} y τ τ {textstyle tau } toma el papel de un parámetro affine. Si la partícula es sin masa Erest{textstyle E_{rm {rest}} es reemplazado por Ekin{textstyle E_{rm {kin}} y mc2{textstyle mc^{2} con hf{textstyle hf}, donde h{textstyle h} es el Planck constante y f{textstyle f} la frecuencia observada localmente.

Solución exacta usando funciones elípticas

La ecuación fundamental de la órbita es más fácil de resolver si se expresa en términos del radio inverso u=1r{textstyle u={frac {1} {} {}}}

()dudφ φ)2=1b2− − ()1− − urs)()1a2+u2){displaystyle left({frac {du}{dvarphi }}right)^{2}={frac {1}{b^{2}}}}}-left(1-ur_{text{s}right)left({fracfrac}}}left({frac}}}left)left {1}{2}}}+u^{2}right)}

El lado derecho de esta ecuación es un polinomio cúbico, que tiene tres raíces, denotado aquí como u1{textstyle u_{1}, u2{textstyle u_{2}, y u3{textstyle u_{3}

()dudφ φ)2=rs()u− − u1)()u− − u2)()u− − u3){displaystyle left({frac {dvarphi }right)^{2}=r_{text{s}}left(u-u-u_{1}right)left(u-u-u-u_{2}right)left(u-u-u-u-u_{3}right)}}

La suma de las tres raíces equivale al coeficiente del u2{textstyle u^{2} mandato

u1+u2+u3=1rs{displaystyle U_{1}+u_{2}+u_{3}={frac} {1}{f}}}} {f}} {f}} {f}}}} {f}}}}}}}}} {f}}}}}}}} {f}}}}} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}} {}}}}}}} {}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

Un polinomio cúbico con coeficientes reales puede tener tres raíces reales, o una raíz real y dos raíces complejas conjugadas. Si las tres raíces son números reales, las raíces se etiquetan para que <math alttext="{textstyle u_{1}<u_{2}u1c)u2c)u3{fnMicrosoftstyle ¿Qué?<img alt="{textstyle u_{1}<u_{2}. Si en lugar de eso hay sólo una raíz real, entonces eso es denotado como u3{textstyle u_{3}; las raíces complejas conjugadas son etiquetadas u1{textstyle u_{1} y u2{textstyle u_{2}. Usando la regla de signos de Descartes, puede haber en la mayoría de una raíz negativa; u1{textstyle u_{1} es negativo si y sólo si <math alttext="{textstyle bbc)a{textstyle b madea}<img alt="{textstyle b. Como se describe a continuación, las raíces son útiles para determinar los tipos de posibles órbitas.

Dado este etiquetado de las raíces, la solución de la ecuación orbital fundamental es

u=u1+()u2− − u1)sn2()12φ φ rs()u3− − u1)+δ δ){displaystyle u=u_{1}+left (u_{2}-u_{1}right),mathrm { sn}left({frac {1}{2}}varphi {sqrt {r_{text{s}}left(u_{3}-u_{1}right)}}}}+deltaright)}}}

Donde sn{textstyle mathrm {sn} representa el sinus amplitudinus función (una de las funciones elípticas Jacobi) y δ δ {textstyle delta } es una constante de integración que refleja la posición inicial. El módulo elíptico k{textstyle k} de esta función elíptica es dada por la fórmula

k=u2− − u1u3− − u1{displaystyle k={sqrt {frac {u_{2}-u_{1}} {u_{3}}}}}

Límite newtoniano

Para recuperar la solución Newtoniana para las órbitas planetarias, uno toma el límite como el radio Schwarzschild rs{textstyle r_{text{s}}} va a cero. En este caso, la tercera raíz u3{textstyle u_{3} se vuelve rudamente 1rs{fnMicroc} {1}{f}}}} {f}} {f}} {f}}}} {f}}}}}}}}} {f}}}}}}}} {f}}}}} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}} {}}}}}}} {}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {, y mucho más grande que u1{textstyle u_{1} o u2{textstyle u_{2}. Por lo tanto, el módulo k{textstyle k} tiende a cero; en ese límite, sn{textstyle mathrm {sn} se convierte en la función sine trigonométrica

u=u1+()u2− − u1)pecado2⁡ ⁡ ()12φ φ +δ δ){displaystyle u=u_{1}+left (u_{2}-u_{1}right),sin ^{2}left({frac {1}{2}varphi +delta right)}

Consecuente con las soluciones de Newton para los movimientos planetarios, esta fórmula describe un conjunto focal de excentricidad e{textstyle e}

e=u2− − u1u2+u1{displaystyle e={frac {u_{2}-u_{1} {u_{2}

Si u1{textstyle u_{1} es un número real positivo, entonces la órbita es un elipse donde u1{textstyle u_{1} y u2{textstyle u_{2} representan las distancias del enfoque más lejano y más cercano, respectivamente. Si u1{textstyle u_{1} es cero o un número real negativo, la órbita es una parabola o una hiperbola, respectivamente. En estos dos últimos casos, u2{textstyle u_{2} representa la distancia del acercamiento más cercano, ya que la órbita va al infinito (u=0{textstyle u=0}), no hay distancia de enfoque más lejano.

Roots and overview of possible orbits

Una raíz representa un punto de la órbita donde el derivado desaparece, es decir, donde dudφ φ =0{fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {f}}} {f}}f}}f}f}fnMicrosoft} {f}}}}f} }=0}. En tal punto de inflexión, u{textstyle u} alcanza un máximo, un mínimo o un punto de inflexión, dependiendo del valor del segundo derivado, que es dado por la fórmula

d2udφ φ 2=rs2[()u− − u2)()u− − u3)+()u− − u1)()u− − u3)+()u− − u1)()u− − u2)]{displaystyle {frac {fnK}u}{dvarphi ¿Qué?

Si las tres raíces son números reales distintos, la segunda derivada es positiva, negativa y positiva en u₁, u₂ y u₃, respectivamente. De ello se deduce que una gráfica de u versus φ puede oscilar entre u₁ y u₂, o puede alejarse de u₃ hacia el infinito (que corresponde a que r vaya a cero). Si u₁ es negativo, sólo parte de una "oscilación" realmente ocurrirá. Esto corresponde a la partícula que viene del infinito, se acerca a la masa central y luego se aleja nuevamente hacia el infinito, como la trayectoria hiperbólica en la solución clásica.

Si la partícula tiene la cantidad correcta de energía para su impulso angular, u₂ y u₃ se fusionará. Hay tres soluciones en este caso. La órbita puede entrar en espiral r=1u2=1u3{textstyle r={frac {1}{u_{2}={frac} {1}{u_{3}}}, acercando ese radio como (asintomáticamente) un exponencial decreciente en φ, τ τ {textstyle tau }o t{textstyle t}. O uno puede tener una órbita circular en ese radio. O uno puede tener una órbita que baja desde ese radio hasta el punto central. El radio en cuestión se llama el radio interior y está entre 32{fnMicroc} {3}{2}} y 3 veces r_s. Una órbita circular también resulta cuando u2{textstyle u_{2} es igual a u1{textstyle u_{1}, y esto se llama el radio exterior. Estos diferentes tipos de órbitas se examinan a continuación.

Si la partícula llega a la masa central con suficiente energía y suficiente bajo impulso angular entonces sólo u1{textstyle u_{1} será real. Esto corresponde a la partícula que cae en un agujero negro. La órbita en espiral con un cambio finito en φ.

Precesión de órbitas

La función sn y su cuadrado sn² tienen períodos de 4K y 2K, respectivamente, donde K i> está definido por la ecuación

K=∫ ∫ 01dSí.()1− − Sí.2)()1− − k2Sí.2){displaystyle K=int ¿Por qué?

Por lo tanto, el cambio en φ sobre una oscilación de u{textstyle u} (o, equivalentemente, una oscilación de r{textstyle r}) iguales

Δ Δ φ φ =4Krs()u3− − u1){displaystyle Delta varphi ={sqrt {r_{text{s}left(u_{3}-u_{1}}}}}}}

En el límite clásico, u₃ enfoques 1rs{fnMicroc} {1}{f}}}} {f}} {f}} {f}}}} {f}}}}}}}}} {f}}}}}}}} {f}}}}} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}} {}}}}}}} {}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { y es mucho más grande que u1{textstyle u_{1} o u2{textstyle u_{2}. Por lo tanto, k2{textstyle k^{2} aproximadamente

k2=u2− − u1u3− − u1.. rs()u2− − u1)≪ ≪ 1{displaystyle k^{2}={frac {u_{2}-u_{1} {u_{3}-u_{1}approx} r_{text{s}left(u_{2}-u_{1}right)ll 1}

Por las mismas razones, el denominador de Δφ es aproximadamente

1rs()u3− − u1)=11− − rs()2u1+u2).. 1+12rs()2u1+u2){displaystyle {frac {1}{sqrt}left(u_{3}-u_{1}right)}}}={frac {1} {sqrt {1-r_{text{}left(2u_{1}+u_{2}}}}}approx 1+{frac {1} {2}r_{text{s}left(2u_{1}+u_{2}right)}}}}} {2}}}{2}} {}}}} {sq}}}}}}}}}}} {sq}}}}}}}}}}}}{1}}}{2}}}}}} {sq}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {sqsqsqsq}}}}}} {sq}}}}}}}} {sqsqsqsqsqsqsqsqsqsq

Desde el módulo k{textstyle k} está cerca de cero, el período K se puede ampliar en los poderes de k{textstyle k}; al orden más bajo, esta expansión produce

K.. ∫ ∫ 01dSí.1− − Sí.2()1+12k2Sí.2)=π π 2()1+k24){displaystyle Kapprox int ¿Qué? {1-y^{2}}left(1+{frac} {1}{2}k^{2}y^{2}right)={frac {pi} ¿Qué?

Sustituyendo estas aproximaciones en la fórmula para Δφ se obtiene una fórmula para el avance angular por oscilación radial

δ δ φ φ =Δ Δ φ φ − − 2π π.. 32π π rs()u1+u2){displaystyle delta varphi =Delta varphi -2piapprox {frac}pi} r_{text{s}left(u_{1}+u_{2}right)}

Para una órbita elíptica, u1{textstyle u_{1} y u2{textstyle u_{2} representan los inversos de las distancias más largas y más cortas, respectivamente. Estos pueden expresarse en términos del eje semi-major del elipse A{textstyle A} y su excentricidad orbital e{textstyle e},

rmax=1u1=A()1+e)rmin=1u2=A()1− − e){displaystyle {begin{aligned}r_{text{max} {frac} {1}{u_{1}}=A(1+e)r_{text{min} {={frac} {1}{u_{2}}=A(1-e)end{aligned}}

dar

u1+u2=2A()1− − e2){displaystyle U_{1}+u_{2}={frac {2}{2}}}}

Sustituyendo la definición rs{textstyle r_{text{s}}} da la ecuación final

δ δ φ φ.. 6π π GMc2A()1− − e2){displaystyle delta varphi approx {frac {6pi GM {c^{2}Aleft(1-e^{2}}}

Desviación de la luz por gravedad

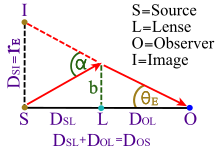
En el límite como la masa de partículas m va a cero (o, equivalentemente si la luz se dirige directamente hacia la masa central, como la longitud a va al infinito), la ecuación para la órbita se convierte

φ φ =∫ ∫ drr21b2− − ()1− − rsr)1r2{displaystyle varphi =int {frac {dr}{2}{sqrt {frac {1}{b^{2}}}}-left(1-{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}}}}} {f}}} {fnMicroc}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {dere} {dere} {r} {dere}}}}}} {r}}}}}}}}} {dere} {r}}}}}}}}}}}}}}}}}}}}}}}} {dere} {dere}}}}} {dere}}}}}}}}}}}}}}}}}}}} {dere}}}}} {1}{2}}}}}} {}}} {}}}}} {}}}}} {}}}}}} {}}}}}}}}}} {}}}}}} {}} {}}}}}}} {}}}} {}}}}}}}} {}}}}}}}}}}}} {}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Ampliación de poderes rsr{fnMicroc} {fnK}} {fnK}}} {fn}}}}} {f}}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}} {f}}}}}} {}}}}}}}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}, el término de orden líder en esta fórmula da la deflexión angular aproximada δφ para una partícula sin masa que viene de la infinidad y volver a la infinidad:

δ δ φ φ.. 2rsb=4GMc2b.{displaystyle delta varphi approx {frac {2r_{text{s}{b}}={frac {frac} {4GM}{c^{2}b}}

Aquí, b{textstyle b} es el parámetro de impacto, algo mayor que la distancia de acercamiento más cercano, r3{textstyle r_{3}:

b=r3r3r3− − rs{displaystyle b=r_{3}{sqrt {frac {fnK}} {f}}} {fnK}}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Aunque esta fórmula es aproximada, es precisa para la mayoría de las mediciones de la lente gravitacional, debido a la pequeñez de la relación rsr{fnMicroc} {fnK}} {fnK}}} {fn}}}}} {f}}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}} {f}}}}}} {}}}}}}}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}. Para la luz que arde la superficie del sol, la deflexión angular aproximada es aproximadamente 1,75 arcos, aproximadamente un millón de partes de un círculo.

Más generalmente, la geodésica de un fotón emitido a partir de una fuente de luz situada en una coordenadas radiales r=1u▪ ▪ [rs,JUEGO JUEGO [{displaystyle r={1over u}in [r_{s],infty [} se puede calcular como sigue, aplicando la ecuación

()dudφ φ)2=rsu3− − u2+1b2{displaystyle {left({du over dvarphi }derecha)}=r_{s}.

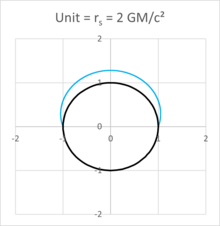
La ecuación se puede derivar como

2dudφ φ d2udφ φ 2=3rsu2dudφ φ − − 2ududφ φ {displaystyle 2 {fnMicroc} {fnMicroc} {fnMicroc}}} {f}}} {fnMicroc} {fnh} {fnh} {fnh}} {fnh}} {f}} {f} {f} {f}}} {f}}}}} {f}} {f}}} {f}}}} {f}}} {f}}}}}}}}} {f}f}}}}}}}}}}} {f}}f}}}}}}}f} {f} {f} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} - Sí. {}{dvarphi }

lo que lleva a

d2udφ φ 2=32rsu2− − u{displaystyle {d^{2}u over dvarphi ^{2}={frac {3}{2}.

Esta ecuación con segundo derivado puede ser numéricamente integrada como sigue por un 4^T orden Método Runge-Kutta, considerando un tamaño de paso Δ Δ φ φ {displaystyle Delta varphi } y con:

k1=d2udφ φ 2()u){displaystyle k_{1}={2}u over dvarphi ^{2}(u)},

k2=d2udφ φ 2()u+Δ Δ φ φ 2dudφ φ){displaystyle k_{2}={2}u over dvarphi ^{2}{bigl (}u+{frac {Delta varphi }{du over dvarphi }{bigr)}},

k3=d2udφ φ 2()u+Δ Δ φ φ 2dudφ φ +Δ Δ φ φ 24k1){displaystyle ¿Qué? Bigl (}u+{frac {Delta varphi {2}{du over dvarphi }+{frac {Delta varphi ¿Qué? Más grande. y

k4=d2udφ φ 2()u+Δ Δ φ φ dudφ φ +Δ Δ φ φ 22k2){displaystyle k_{4}={2}u over dvarphi ^{2}{Bigl (}u+Delta varphi {du over dvarphi }+{frac {Delta varphi ¿Qué?.

El valor en el siguiente paso dudφ φ ()φ φ +Δ Δ φ φ){displaystyle {du over dvarphi }(varphi +Delta varphi)} es

dudφ φ ()φ φ)+Δ Δ φ φ 6()k1+2k2+2k3+k4){displaystyle {du over dvarphi }(varphi)+{frac {Delta varphi ¿Qué?

y el valor en el siguiente paso u()φ φ +Δ Δ φ φ){displaystyle u(varphi +Delta varphi)} es

u()φ φ)+Δ Δ φ φ dudφ φ ()φ φ)+Δ Δ φ φ 26()k1+k2+k3){displaystyle u(varphi)+ Delta varphi {du over dvarphi }(varphi)+{frac {Delta varphi ¿Qué?

El paso Δ Δ φ φ {displaystyle Delta varphi } puede ser elegido para ser constante o adaptable, dependiendo de la exactitud requerida en r=1u{displaystyle r={1over u}.

Relación con la física newtoniana

Energía potencial radial efectiva

La ecuación de movimiento de la partícula derivada arriba

()drdτ τ)2=E2m2c2− − c2+rsc2r− − L2mμ μ r2+rsL2mμ μ r3{displaystyle left({frac {dtau }right)^{2}={frac} [E^{2} {m^{2}c^{2}}-c^{2}+{frac} {fnMicrosoft Sans} {fnMicroc} {fnMicroc} {fnK}} {fnK}} {fnMicroc}} {f}}} {f}} {f}} {f}}} {f}}}}}} {f}}}} {f}}}} {f}} {f}}} {f}}}}} {f}}}}}}}}}} { {fnK}} {mmm}} {mm}}}} {mm}}} {mmmm} {m}}}}} {mm} {m}}}}} {mmmmmm}}} {mmmm}}}}}}}} {mm}}}}}}}}}}}} {mmmmmmmmmmmmmmmmmmmmmm}}}}}}}}}}}}}}}}}} {mmmmmmmmmmmmmmmmmmm}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

puede reescribirse utilizando la definición del radio de Schwarzschild r_s como

12m()drdτ τ)2=[E22mc2− − 12mc2]+GMmr− − L22μ μ r2+G()M+m)L2c2μ μ r3,{displaystyle {frac {2}mleft({frac {dr}{dtau ¿Qué? {E^{2}{2mc^{2}}-{frac} {1}{2}mc^{2}derecha]+{frac {GMm}{frac} {L^{2}{2}}+{frac {G(M+m)L^{2}}{c^{2}mu r^{3}}}}}}}

que es equivalente a una partícula que se mueve en un potencial único

V()r)=− − GMmr+L22μ μ r2− − G()M+m)L2c2μ μ r3{displaystyle V(r)=-{frac {GMm} {r}+{frac} {fnK} {fnK} {fnK}} {fnK}} {fnK}}}}} {c}}m}}}} {f}}}}}}} {fnK}}}}}}}} {f}}} {f}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}} {m}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}} {m} {m} {m}} {m}}}}}} {m}}}} {m}}}}}}}} {m}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Los dos primeros términos son energías clásicas bien conocidas, siendo el primero la energía potencial gravitacional newtoniana de atracción y el segundo correspondiente a la energía potencial gravitacional repulsiva "centrífuga". energía potencial; sin embargo, el tercer término es una energía atractiva exclusiva de la relatividad general. Como se muestra a continuación y en otros lugares, esta energía cúbica inversa hace que las órbitas elípticas precedan gradualmente en un ángulo δφ por revolución.

δ δ φ φ.. 6π π G()M+m)c2A()1− − e2){displaystyle delta varphi approx {6pi G(M+m)}{c^{2}Aleft(1-e^{2}right)}}}

Donde A{textstyle A} es el eje semi-major e{textstyle e} es la excentricidad.

El tercer término es atractivo y domina a pequeña r{textstyle r} valores, dando un radio interior crítico r_interior a la cual se dibuja una partícula inexorablemente hacia r=0{textstyle r=0}; este radio interior es una función del impulso angular de la partícula por masa unidad o, equivalentemente, el a{textstyle a} longitud-scale definida arriba.

Órbitas circulares y su estabilidad

El potencial eficaz V{textstyle V} puede ser re-escrito en términos de la longitud a=hc{textstyle a={frac {h}{c}}.

V()r)=μ μ c22[− − rsr+a2r2− − rsa2r3]{displaystyle V(r)={frac {mu c^{2}{2}left[frac] {fnMicrosoft Sans} {fnMicroc} {fnMicroc}} {fnMicroc}}} {f}} {fn}} {fnMicroc}}}}}}}} {fn}}}}}} {fnf}}}}fnMicroc}}}}}}}}}}}}}}} {\\\fn\\fnMicrocfn}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\fn\fnMicrocfn\fnMicrocfn}}}}}}}}}}}}}}}}\\\\fn}}\ {fnMicroc} {fnMicroc} {fnMicrosoft Sans Serif}

Las órbitas circulares son posibles cuando la fuerza efectiva es cero

F=− − dVdr=− − μ μ c22r4[rsr2− − 2a2r+3rsa2]=0{displaystyle F=-{frac {fnK} {fnMicroc {fnK} {2r}}left[r_{text{}r^{2}-2a^{2}r+3r_{}a}a^{2}right}=0}

es decir, cuando las dos fuerzas de atracción (la gravedad newtoniana (primer término) y la atracción exclusiva de la relatividad general (tercer término)) están exactamente equilibradas por la fuerza centrífuga repulsiva (segundo término). Hay dos radios en los que puede ocurrir este equilibrio, indicados aquí como r_interior y r_exterior

rexterior=a2rs()1+1− − 3rs2a2)rinterior=a2rs()1− − 1− − 3rs2a2)=3a2rexterior{displaystyle {begin{aligned}r_{text{outer} {begin{begin{aligned}r_{text{outer} {a}{2} {r_{text{s}}}left(1+{sqrt {1-{2}}}derecha)[3pt]r_{text{inner} {={frac}}}derecha)[3pt]r_{text{inner}} {={frac} {a}{2} {r_{text{s}}}left(1-{sqrt {1-{2}}}derecha)={frac} {3a^{2} {f} {fnK}} {fnK}}} {fnK}}} {fn}}}} {fn}}} {fnK}}}}}}} {fn}}}}}} {f}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}} {f}}}} {f}} {f}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

que se obtienen mediante la fórmula cuadrática. El radio interior r_inner es inestable, porque la tercera fuerza atractiva se fortalece mucho más rápido que las otras dos fuerzas cuando r se vuelve pequeña; si la partícula se desliza ligeramente hacia adentro desde r_interior (donde las tres fuerzas están en equilibrio), la tercera fuerza domina a las otras dos y atrae inexorablemente a la partícula hacia adentro hacia . r = 0. Sin embargo, en el radio exterior las órbitas circulares son estables; el tercer término es menos importante y el sistema se comporta más como el problema no relativista de Kepler.

Cuando a{textstyle a} es mucho mayor que rs{textstyle r_{text{s}}} (el caso clásico), estas fórmulas se vuelven aproximadamente

rexterior.. 2a2rsrinterior.. 32rs{displaystyle {begin{aligned}r_{text{outer} {frac {2a^{2}{r_{text{s}}}}[3pt]r_{text{inner}} {frac {f} {f}}} {f}}}} {f}}}}f}f}f}f}f}f}}f}f}f}f}f}}f}f}f}f}f}}f}f}f}f}fnKf}}f}f}}}f}f}}f}f}f}}}}f}}}}f}}}f}f}f}f}f}f}f}f}}fnKfnKf}}}fnKf}}fnKf}}}}}}

Sustituir las definiciones de a{textstyle a} y r_s en r_exterior produce la fórmula clásica para una partícula de masa m{textstyle m} orbitando un cuerpo de masa M{textstyle M}.

router3=G()M+m)⋅ ⋅ φ φ 2{displaystyle r_{mathrm {outer} {}{3}={frac {G(M+m)}{omega _{varphi } {2}}}

donde ω_φ es la velocidad angular orbital de la partícula. Esta fórmula se obtiene en mecánica no relativista igualando la fuerza centrífuga a la fuerza gravitacional newtoniana:

GMmr2=μ μ ⋅ ⋅ φ φ 2r{displaystyle {frac {GMm}{2}=mu} omega _{varphi } {2}r}

Donde μ μ {textstyle mu } es la masa reducida.

En nuestra notación, la velocidad angular orbital clásica es igual

⋅ ⋅ φ φ 2.. GMrouter3=()rsc22router3)=()rsc22)()rs38a6)=c2rs416a6{displaystyle omega _{varphi }{2}approx {fnMicroc {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicroc} {fnMicroc} {f}}}} {\\\\fnMicrocH\fnMicrocH\fnMicrocHfnMicrocHfnMicrocH\\\fnMicrocH\fnMicrocH\\fnMicrocH0}\fnMicrocH0}m}m}m}\\\fnMicrocH0}m}m} } {}}=left({frac {fnK} {fnK}} {fnh00}}}}}derecha)=eft({frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicroc}} {fnK}} {fnK} {fnK}}} {fnMicroc}}}}} {fnKf}}} {f}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}} {f} {f}} {f}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f}} {f}}}}} {f} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {fnK} {fnK}} {fnK}}} {fn}}}} {c}}}} {c}} {c}}}}} {c}}}}}} {c}}} {c}}}}}}}} {c}}}} {c}}}}}} {c}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}} {c}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

En el otro extremo, cuando a² se acerca a 3r_s² desde arriba, los dos radios convergen en un único valor

router.. rinner.. 3rs{displaystyle r_{mathrm {outer}approx r_{mathrm {inner}approx 3r_{text{s}}

Las soluciones cuadráticas anteriores garantizan que r_outer sea siempre mayor que 3r_s, mientras que r_interior se encuentra entre 3⁄2 r_s y 3r_s. Órbitas circulares menores que 3⁄2 r_s no son posibles. Para partículas sin masa, a llega al infinito, lo que implica que hay una órbita circular para los fotones en r_inner = 3⁄2r_s. La esfera de este radio a veces se conoce como esfera de fotones.

Precesión de órbitas elípticas

La tasa de precesión orbital se puede derivar utilizando este potencial radial efectivo V. Una pequeña desviación radial de una órbita circular de radio r_exterior oscilará establemente con una frecuencia angular

⋅ ⋅ r2=1m[d2Vdr2]r=router{displaystyle omega ¿Qué? {2}{2}}derecha]_{r=r_{mathrm {outer}

que es igual

⋅ ⋅ r2=()c2rs2router4)()router− − rinner)=⋅ ⋅ φ φ 21− − 3rs2a2{displaystyle omega _{2}=left({frac^{2}r_{text{s}}}{2r_{mathrm {outer}} {4}}right)left(r_{mathrm {outer} }-r_{mathrm {inner} {ego} {} {}}}}}}}} {m}}}}}}}} {m}}}} {m}}}}}}}}} {m} {m}}}}} {m}}}} {m}}}}}}}}}}}}}}}}}}}}}}} {m} {m}} {m} {m}} {m}}}}}} {m}}}}}}}}}}}}}}}}}}}}}} {m}} {m}}}}}} {m}}}}}}}}}}} {fnMicrosoft Sans}}}}

Tomar la raíz cuadrada de ambos lados y realizar una expansión en serie de Taylor produce

⋅ ⋅ r=⋅ ⋅ φ φ [1− − 3rs24a2+O()rs4a4)]{displaystyle omega ################################################################################################################################################################################################################################################################ _{varphi }left[1-{frac {text{}{2}{4a^{2}}}}+{mathcal {O}}left({frac} {fnMicroc} {fnMicrosoft Sans Serif}

Multiplicación por el período T de una revolución da la precesión de la órbita por revolución

δ δ φ φ =T()⋅ ⋅ φ φ − − ⋅ ⋅ r).. 2π π ()3rs24a2)=3π π m2c22L2rs2{displaystyle delta varphi =Tleft(omega) _{varphi }-omega ¿Por qué? ¿Qué?

donde hemos usado ⋅_φT = 2п y la definición de la longitud a. Sustituyendo la definición del radio Schwarzschild r_s da

δ δ φ φ.. 3π π m2c22L2()4G2M2c4)=6π π G2M2m2c2L2{displaystyle delta varphi approx {frac {3pi ########## {fnMicroc {4G^{2}} {2}} {4}}}derecho)={frac} {6fncH00} - ¿Sí?

Esto puede ser simplificado usando la semiaxis de la órbita elíptica A y excentricidad e relacionados con la fórmula

h2G()M+m)=A()1− − e2){displaystyle {frac {h^{2}{G(M+m)}=Aleft(1-e^{2}right)}

para dar el ángulo de precesión

δ δ φ φ.. 6π π G()M+m)c2A()1− − e2){displaystyle delta varphi approx {6pi G(M+m)}{c^{2}Aleft(1-e^{2}right)}}}

Derivaciones matemáticas de la ecuación orbital

Símbolos de Christoffel

Los símbolos de Christoffel que no desaparecen para la métrica de Schwarzschild son:

.. rtt=− −.. rrr=rs2r()r− − rs).. ttr=rs()r− − rs)2r3.. φ φ φ φ r=()rs− − r)pecado2⁡ ⁡ ()Silencio Silencio).. Silencio Silencio Silencio Silencio r=rs− − r.. rSilencio Silencio Silencio Silencio =.. rφ φ φ φ =1r.. φ φ φ φ Silencio Silencio =− − pecado⁡ ⁡ ()Silencio Silencio)#⁡ ⁡ ()Silencio Silencio).. Silencio Silencio φ φ φ φ =cot⁡ ⁡ ()Silencio Silencio){displaystyle {begin{aligned} Gamma... {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} Gamma _{theta theta }{r} {text{s}-r[3pt] Gamma _{rtheta. }=Gamma _{phi } {frac {1}{}[3pt]Gamma _{phi phi }{theta } {theta=-sin(theta)cos(theta)[3pt][3pt] Gamma _{theta phi } {fi } {fnunció}}}

Ecuación geodésica

Según la teoría de la relatividad general de Einstein, partículas de masa insignificante viajan a lo largo de geodésicas en el espacio-tiempo. En el espacio-tiempo plano, lejos de una fuente de gravedad, estas geodésicas corresponden a líneas rectas; sin embargo, pueden desviarse de las líneas rectas cuando el espacio-tiempo es curvo. La ecuación de las líneas geodésicas es

d2xλ λ dq2+.. μ μ.. λ λ dxμ μ dqdx.. dq=0{displaystyle {frac {f}x}{lambda } {dq^{2}} Gamma _{munu }{lambda ¿Qué? ¿Qué? } {dq}=0}

donde la luminaria representa el símbolo Christoffel y la variable q{textstyle q} parametriza el camino de la partícula a través del espacio-tiempo, su llamada línea mundial. El símbolo Christoffel depende sólo del tensor métrico gμ μ.. {textstyle g_{munu}}, o más bien sobre cómo cambia con posición. La variable q{textstyle q} es una constante múltiple del tiempo adecuado τ τ {textstyle tau } para órbitas temporales (que son viajadas por partículas masivas), y se suele tomar para ser igual a ella. Para órbitas livianas (o nulas) (que son transitadas por partículas sin masa como el fotón), el tiempo adecuado es cero y, estrictamente hablando, no se puede utilizar como la variable q{textstyle q}. Sin embargo, las órbitas ligeras pueden derivarse como el límite ultrarelativista de órbitas temporales, es decir, el límite como la masa de partículas m va a cero mientras mantiene su energía total fija.

Por lo tanto, para resolver el movimiento de una partícula, la forma más directa es resolver la ecuación geodésica, un enfoque adoptado por Einstein y otros. La métrica Schwarzschild puede ser escrita como

c2dτ τ 2=w()r)c2dt2− − v()r)dr2− − r2dSilencio Silencio 2− − r2pecado2⁡ ⁡ Silencio Silencio dφ φ 2{displaystyle c^{2}dtau ^{2}=w(r)c^{2}dt^{2}-v(r)dr^{2}-r^{2}dtheta ^{2}-r^{2}sin ^{2}theta dphi ^{2},}

donde las dos funciones w()r)=1− − rsr{textstyle w(r)=1-{frac {text{s} {}{r}}}} {f}} {f}}} {f}}} {f}} {f}}} {f}}}}} {f}} {f}}}}}y su reciprocidad v()r)=1w()r){textstyle v(r)={frac {1}{w(r)}}se definen para la brevedad. De esta métrica, los símbolos de Christoffel .. μ μ.. λ λ {textstyle Gamma _{munu }{lambda }puede ser calculado, y los resultados sustituidos en las ecuaciones geodésicas

0=d2Silencio Silencio dq2+2rdSilencio Silencio dqdrdq− − pecado⁡ ⁡ Silencio Silencio #⁡ ⁡ Silencio Silencio ()dφ φ dq)20=d2φ φ dq2+2rdφ φ dqdrdq+2cot⁡ ⁡ Silencio Silencio dφ φ dqdSilencio Silencio dq0=d2tdq2+1wdwdrdtdqdrdq0=d2rdq2− − 1vdvdr()drdq)2− − rv()dSilencio Silencio dq)2− − rpecado2⁡ ⁡ Silencio Silencio v()dφ φ dq)2+c22vdwdr()dtdq)2{displaystyle {begin{aligned}0 ventaja={frac {d^{2}theta - ¿Qué? {2} {fn} {fnK} {fnK}} {fnK}} {fn} {fnK} {f}}} {f}}}} {fn} {fn}} {fn} {f}}} {f}}} {fnfnMicroc {f} {f}} {f}}}}}} {f}f}}}}}}f} {f}f} {f}f}f}f} {f}f} {f}f}f}f} {f}f}f}f}f} {f} {f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f }{dq}{frac {dr}{dq}-sin theta cos theta left({frac {dphi }{dq}right)^{2}[3pt]0 limit={frac {d^{2}phi] - ¿Qué? {2} {fn} {fnMicroc} {fnK} {fnMicroc}} {fnK} {f}} {fn}} {fn}}} {fn}}} {fn}} {f}}} {fn} {fnK}} {fnK}}} {f} {f} {f}f}}}}}f}} {f} {f}f}f}}f}f}f}f}f}f}f}fn}f}f}f}f}f}f}f}f}f}fn}f}fn}f}f}f}f}f}f}f}f}fn}fn}f}f}f}fn}f}f}f}}f}fn {fnK}+2theta {fnMicroc {dfnh}fnhfnh} }{dq}{frac {dtheta ################################################################################################################################################################################################################################################################ {fnMicroc} {1} {fn} {fnK} {fnK}} {fnMicroc} {fn}} {fn}} {fn}}} {fn}} {fn}}} {fn} {fn}}} {f} {f}}} {fn}}} {f} {f} {f} {f} {f}}f}f}}f}f}f}f}}f}f} {f} {f} {f} {f}f} {f}f} {f}f}f}f}}f}f}fn}f}fn}}}}f}f} {f}f}f}f} {f} {fn}fn}f}f}f}f}}f}f}f} {fn} {dt}{dq}{frac} {dr}{dq}[3pt]0 {fnMicroc} {1}{}{frac {dr}left({frac} {f} {fnh} {fnh}} {f}}} {f} {f}}} {fn} {fn}} {f}}} {f} {f}f}f}f}f}f}f} {f} {f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}fn}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fn}f}f}f}f}f}f}f}f}f}fn {fn} {fnK}fnMicroc {f}fnh} {fnMicroc {dtheta} {f}}derecho)}-{2}-{frac {rsin ^{2}theta {fnMicrosoft Sans Serif} {fnK} {f} {fnK}f}fnh}m} {fnMicroc} {fn} {fnK}} {f}} {fnK}}} {f}}} {f}}} {f}} {f}} {fnK}}}} {f}}}}}} {f}}}}} {f} {f} {f} {f}f}f}f}f}f}f} {f} {f} {f}f}f}f}f}f}f}f}}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}fn {dt} {dq}right) {2}end{aligned}}

Puede verificarse que Silencio Silencio =π π 2{textstyle theta ={frac {cHFF} } {2}} es una solución válida por sustitución en la primera de estas cuatro ecuaciones. Por simetría, la órbita debe ser planaria, y somos libres de organizar el marco de coordenadas para que el plano ecuatorial sea el plano de la órbita. Esto Silencio Silencio {textstyle theta } solución simplifica las ecuaciones segunda y cuarta.

Para resolver las ecuaciones segunda y tercera, basta dividirlas por dφ φ dq{fnMicroc} {dfnK} } {dq}} y dtdq{fnMicroc} {dt}{dq}}, respectivamente.

0=ddq[In⁡ ⁡ dφ φ dq+In⁡ ⁡ r2]0=ddq[In⁡ ⁡ dtdq+In⁡ ⁡ w],{displaystyle {begin{aligned}0 ventaja={frac {dq}left[lnn] {fnMicroc {fnMicroc} } {dq}+ln ################################################################################################################################################################################################################################################################ {fnMicroc {dt}{dq}+ln wright],end{aligned}

lo que produce dos constantes de movimiento.

Enfoque lagrangiano

Debido a que las partículas de prueba siguen la geodésica en una métrica fija, las órbitas de esas partículas pueden determinarse utilizando el cálculo de las variaciones, también llamado el enfoque lagrangiano. La geodésica en el espacio-tiempo se define como curvas para las cuales pequeñas variaciones locales en sus coordenadas (mientras sostienen sus eventos de punto final fijo) no hacen ningún cambio significativo en su longitud general s. Esto se puede expresar matemáticamente utilizando el cálculo de las variaciones

0=δ δ s=δ δ ∫ ∫ ds=δ δ ∫ ∫ gμ μ.. dxμ μ dτ τ dx.. dτ τ dτ τ =δ δ ∫ ∫ 2Tdτ τ {displaystyle 0=delta s=delta int ds=delta int {sqrt {g_{munu }{frac {fnh00} } {dtau }{frac {fnK} {f}}dtau =delta int {sqrt {2T}dtau }

donde τ es el tiempo adecuado, s = cτ es la longitud del arco en el espacio-tiempo y T se define como

2T=c2=()dsdτ τ)2=gμ μ.. dxμ μ dτ τ dx.. dτ τ =()1− − rsr)c2()dtdτ τ)2− − 11− − rsr()drdτ τ)2− − r2()dφ φ dτ τ)2{displaystyle 2T=c^{2}=left({frac {dtau }right)^{2}=g_{munu }{frac {fnh00} } {dtau ¿Qué? Está bien.

en analogía con la energía cinética. Si la derivada con respecto al tiempo propio se representa con un punto por brevedad

xÍ Í μ μ =dxμ μ dτ τ {displaystyle { dot {x}}{mu} }={frac {dx^{mu } {dtau }

T puede escribirse como

2T=c2=()1− − rsr)c2()tÍ Í)2− − 11− − rsr()rÍ Í)2− − r2()φ φ Í Í)2{displaystyle {fnMicrosoft Sans Serif} {fnMicroc} {fnMicroc} {fnMicroc} {f} {f}} {f}} {f}} {fnMicroc}} {f} {f}} {f}} {f}}} {f}} {f}}}} {f}}} {f}}}}} {f}}}}}}}}}}}}}}}} {f} {f} {f}}} {f}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Los factores constantes (como c o la raíz cuadrada de dos) no afectan la respuesta al problema variacional; por lo tanto, tomando la variación dentro de la integral se obtiene el principio de Hamilton

0=δ δ ∫ ∫ 2Tdτ τ =∫ ∫ δ δ T2Tdτ τ =1cδ δ ∫ ∫ Tdτ τ.{displaystyle 0=delta int {sqrt {2T}dtau =int {frac} {delta # {sqrt {2T}dtau ={frac {1} {c}delta int Tdtau.}

La solución del problema variacional viene dada por las ecuaciones de Lagrange.

ddτ τ ()∂ ∂ T∂ ∂ xÍ Í σ σ)=∂ ∂ T∂ ∂ xσ σ.{displaystyle {frac {d}dtau }left({frac {partial T}{dot {dot {x}}} {sigma }}}right)=frac {partial T}{sigma}{sigma}}}}sigma}}}}right)=frac }}}

Cuando se aplican a t y φ, estas ecuaciones revelan dos constantes de movimiento

ddτ τ [r2dφ φ dτ τ ]=0,ddτ τ [()1− − rsr)dtdτ τ ]=0,{displaystyle {begin{aligned}{frac}{dtau {fnK} {fnMicroc {dvarphi}{dtau }right=0,\{f}{dtau }left[left(1-{text{}}{r}}right){frac {dt}{dtau }}}right} {}}}=0,end{aligned}}}

que puede expresarse en términos de dos escalas de longitud constantes, a{textstyle a} y b{textstyle b}

r2dφ φ dτ τ =ac,()1− − rsr)dtdτ τ =ab.{displaystyle {begin{aligned}r^{2}{frac {dvarphi }{dtau } {=ac,\\left(1-{frac {text{}}{}r}right){frac} {frac}}}frac}} {fnMicroc}}} {dt}{dtau ♪♪♪ {a}{b}.

Como se muestra anteriormente, la sustitución de estas ecuaciones en la definición de la métrica Schwarzschild produce la ecuación para la órbita.

Enfoque Hamiltoniano

Una solución lagrangiana se puede retransmitir en una forma equivalente Hamiltonian. En este caso, el Hamiltonian H{displaystyle H. es dado por

2H=c2=pt2c2()1− − rsr)− − ()1− − rsr)pr2− − pSilencio Silencio 2r2− − pφ φ 2r2pecado2⁡ ⁡ Silencio Silencio {displaystyle 2H=c^{2}={frac [p_{t} {2} {c^{2}left(1-{frac} {c} {c} {c} {c}} {c}c}c}c}c}c}cc}c}c}cc}c}c}c}c}c}left(1-{c} {c} {c} {c} {c} {c}c}c}c}c}c}c} {c}c}{c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}cc}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c} {fnMicroc {fnMicrosoft Sans Serif}} {fnMicroc {fnMicroc {f}}} {r}}}}right)p_{r}{2}-{frac} {fnMicroc}}}}}} {r}}}} {r}}}}}}}} {f}}}}}} {f}}}}}} {f}}}}}}}}}}}}}} {f}} {f}}}}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}} {p}}}}}}}}}}} {p}}}}} {f}}}}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicroc} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ^{2}theta }

Una vez más, la órbita puede limitarse a Silencio Silencio =π π 2{textstyle theta ={frac {cHFF} } {2}}por simetría. Desde t{textstyle t} y φ φ {textstyle varphi } no aparecen en el Hamiltonian, su conjugado momenta son constantes; pueden expresarse en términos de la velocidad de la luz c{textstyle c} y dos escalas de longitud constantes a{textstyle a} y b{textstyle b}

pφ φ =− − acpSilencio Silencio =0pt=ac2b{displaystyle {begin{aligned}p_{varphi ♪♪♪♪ - ¿Qué? {C}} {fn} {fnK}} {fn}} {fnK}}} {fn}} {fn}} {fn}} {fn}}}} {fn}}}} {fn}}}} {fn}}}}}} {fnK}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Los derivados con respecto al tiempo adecuado son dados por

drdτ τ =∂ ∂ H∂ ∂ pr=− − ()1− − rsr)prdφ φ dτ τ =∂ ∂ H∂ ∂ pφ φ =− − pφ φ r2=acr2dtdτ τ =∂ ∂ H∂ ∂ pt=ptc2()1− − rsr)=ab()1− − rsr){displaystyle {begin{aligned}{frac {d}{dtau ♪♪♪♪♪frac {partial H'{partial {fnMicrosoft Sans} {fnMicroc} {fnMicroc} {fnMicrosoft Sans Serif} {f}}fnMicroc} {dvarphi }{dtau ♪♪♪♪♪frac {partial H'{partial P_{varphi }={frac {-p_{varphi {} {fn}} {fnK}}\fnK}\fnfnMic} {dt}{dtau ♪♪♪♪♪frac {partial H'{partial ¿Qué? {fn} {c}cc}left(1-{frac} {fnh} {c}cc}cc}c}cc}c}c}cccc}cc}cc}c}ccc}ccc}c}c}c}c}c}c}c}ccccccc}c}c}c}cccc}ccc}cccccccc}c}c}c}c}c}ccc}c}ccccccccc}c}c}c}cccc}c}cc}c}c}c}cc {fnK}} {fnMicroc {fnMicroc}}}end{aligned}}}} {f}}}}}}}} {f}}} {f}}}}} {f}}} {f}}}} {f}} {f}}}} {f}}}}} {f}}}}}}}}}}}}} {f} {f}}}}f}}}}}}} {f} {f} {f}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f}} {f}}}}}}}}}}f}}}}}}}}}}}}}}f} {f} {f}}

Dividir la primera ecuación por segundo produce la ecuación orbital

drdφ φ =− − r2ac()1− − rsr)pr{displaystyle {frac {}{dvarphi }=-{frac {r^{2}{ac}left(1-{frac} {fnMicrosoft Sans Serif}

El impulso radial p_r se puede expresar en términos de r usando la constancia del Hamiltonian H=c22{textstyle H={frac {c}{2}}} {2}}}}} {c}} {c}}} {c}}} {c}}}}}}}} {c} {c}}}} {c}}}}} {c}}}}}} {c}}} {c}}}} {c}}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}} {}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}; esto produce la ecuación orbital fundamental

()drdφ φ)2=r4b2− − ()1− − rsr)()r4a2+r2){displaystyle left {frac {dvarphi }}right)^{2}={frac {4}{b^{2}}}}-left(1-{frac {frac}} {b}} {b}}}} Está bien. {fnK} {fnMicrosoft Sans Serif}

Enfoque Hamilton-Jacobi

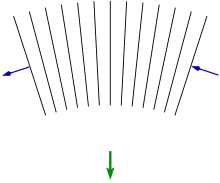
La ecuación orbital se puede derivar de la ecuación de Hamilton-Jacobi. La ventaja de este enfoque es que equipara el movimiento de la partícula con la propagación de una onda y conduce claramente a la derivación de la desviación de la luz por la gravedad en la relatividad general, a través del principio de Fermat. La idea básica es que, debido a la desaceleración gravitacional del tiempo, las partes de un frente de onda más cercanas a una masa gravitante se mueven más lentamente que las más alejadas, desviando así la dirección de propagación del frente de onda.

Usando la covarianza general, la ecuación de Hamilton-Jacobi para una sola partícula de masa unitaria se puede expresar en coordenadas arbitrarias como

gμ μ.. ∂ ∂ S∂ ∂ xμ μ ∂ ∂ S∂ ∂ x.. =c2.{displaystyle g^{munu }{frac {cMicrosoft Sans Serif} S'{partial x^{mu {fnMicrosoft Sans Ser} {fnMicrosoft Sans Ser} {fnMicrosoft Sans Ser} {fn} {fn}} {fn}}}} {fn}}}}} {fnfn} {fnfnf}fn}fnfnfnfnfnfnfnfn}fn}fnfn}fn}fnfnfn}fnfn}fn}fnfnfn}fnfnfnfnfnfnfnfnfn}fnfnfnfn}fn}\fnfnfn}fnfn}fn}fnfnfnfn\fnfn}fn }=c^{2}

Esto es equivalente a la formulación hamiltoniana anterior, donde las derivadas parciales de la acción reemplazan a los momentos generalizados. Usando la métrica de Schwarzschild g^μν, esta ecuación se convierte en

1c2()1− − rsr)()∂ ∂ S∂ ∂ t)2− − ()1− − rsr)()∂ ∂ S∂ ∂ r)2− − 1r2()∂ ∂ S∂ ∂ φ φ)2=c2{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}} {fnMicroc {partial S}}right)}}}left({frac {f}{f} {f} {f} {fnMicroc}} {f}}}}}}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnKfnKfnKfnKf}f}fnKfnKfnKfnKfnKfnKfnKfnKfnMinKf}fnKf}}fnMi {partial S}{partial r}}right)}{2}-{frac {1}{2}}}left({frac {partial S}{partial varphi }}right)}{2}=c^{2}}}}}}}}}}}}}}}}}} {derechac}} {dere}} {dere}}} {c}}}}}}{dere}}}}}}} {c} {dere} {dere} {c} {c} {c}}}}}}}}}}}}}}}}}}}}}}}}} {c} {dere}}}}} {c}} {c}}}} {dere}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

donde nuevamente orientamos el sistema de coordenadas esféricas con el plano de la órbita. El tiempo t y el ángulo azimutal φ son coordenadas cíclicas, por lo que la solución de la función principal de Hamilton S se puede escribir

S=− − ptt+pφ φ φ φ +Sr()r){displaystyle S=-p_{t}t+p_{varphi }varphi +S_{r}(r),}

Donde pt{displaystyle P_{t} y pφ φ {displaystyle p_{varphi } son el momento generalizado constante. La ecuación Hamilton-Jacobi ofrece una solución integral para la parte radial Sr()r){displaystyle S_{r}(r)}

Sr()r)=∫ ∫ rdr1− − rsrpt2c2− − ()1− − rsr)()c2+pφ φ 2r2).{displaystyle S_{r}(r)=int ^{r}{frac {dr}{1-{frac} {fnMicroc}} {fnK}} {fnMicroc}} {f}}} {f}} {f}}} {fn}}} {f}}}}}} {fn}}}} {f}}}}} {f} {f}}}}}}}} {sqf}}}}}} {f}}}}} {f}}}}}}} {f}}}}}}}} {sqsqf} {f} {f}} {f}} {f} {f}}} {f}}}}}}}}}}}}} {sqsqf} { sqsqsqf} {sqsqf}}} {f}}}}} {f}}}}}}}} {f} {sqf}}}} {f}}}}} [p_{t} {2} {c^{2}}}-left(1-{frac} {c} {c} {c} {c} {c}} {c}} {c}} {c}}} {c}} {c}}} {c}}}}}}}c}}}left(1- {left(1-{c} {eff}{c}{c} {c} {c} {c} {c} {c} {c}{c}{c} {c}{c}}}}}}} {c}}}}} {c} {c} {c}}}} {c} {c}} {c} {c}}}}}} {c}}}}} {c}}}} {c}{c}}}}}}}}}}}} {c}}}}}} {fnMicrosoft Sans Serif} {cHFF} - Sí.

Tomando el derivado de la función principal de Hamilton S con respecto al impulso conservado p_φ rendimientos

∂ ∂ S∂ ∂ pφ φ =φ φ +∂ ∂ Sr∂ ∂ pφ φ =constant{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft} S'{partial p_{varphi }=varphi +{frac {partial S_{r}{partial P_{varphi }=mathrm {constant}

que es igual

φ φ − − ∫ ∫ rpφ φ drr2pt2c2− − ()1− − rsr)()c2+pφ φ 2r2)=constant{displaystyle varphi -int ^{r}{frac {fnMicrosoft} {fnMicrosoft} {fnMicroc} {fnMicroc} {fnK} {f}} {fn} {fnK}} {fnK} {fnK} {f}} {fnKf}} {fnKfnK}} {f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnf}f}f}f}f}f}f}f}f}f}f}fnf}}f}f}f}fnf}f}f}f}f}fnfnfnf}fnf}}}}f}}}}}}fn [p_{t} {2} {c^{2}}}-left(1-{frac} {c} {c} {c} {c} {c}} {c}} {c}} {c}}} {c}} {c}}} {c}}}}}}}c}}}left(1- {left(1-{c} {eff}{c}{c} {c} {c} {c} {c} {c} {c}{c}{c} {c}{c}}}}}}} {c}}}}} {c} {c} {c}}}} {c} {c}} {c} {c}}}}}} {c}}}}} {c}}}} {c}{c}}}}}}}}}}}} {c}}}}}} {fnMicrosoft Sans Serif} {cHFF} {fnMicrosoft Sans Serif}}=mathrm {constant}

Tomando una variación infinitesimal en φ y r se obtiene la ecuación orbital fundamental

()drdφ φ)2=r4b2− − ()1− − rsr)()r4a2+r2).{displaystyle left {frac {dvarphi }}right)^{2}={frac {4}{b^{2}}}}-left(1-{frac {frac}} {b}} {b}}}} Está bien. {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

donde las escalas de longitud conservadas a y b están definidas por los momentos conservados por las ecuaciones

∂ ∂ S∂ ∂ φ φ =pφ φ =− − ac∂ ∂ S∂ ∂ t=pt=ac2b{displaystyle {begin{aligned}{frac {partial S}{partial varphi }=p_{varphi } {partial S}{partial t}=p_{t} {C}} {fn} {fnK}} {fn}} {fn}} {fn}} {fn}} {fn}}} {fn}}}}} {fn}}}}}}}}}} {fn}}}}}}}} {fnK}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}} {f} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

El principio de Hamilton

La integral de acción para una partícula afectada sólo por la gravedad es

S=∫ ∫ − − mc2dτ τ =− − mc∫ ∫ cdτ τ dqdq=− − mc∫ ∫ − − gμ μ.. dxμ μ dqdx.. dqdq{displaystyle S=int {-mc^{2}dtau #=-mcint {c{frac {dtau # {dq}dq}=-mcint {sqrt {-g_{munu}{frac {fnh00} ¿Qué? - Sí.

Donde τ τ {textstyle tau } es el tiempo adecuado y q{textstyle q} es cualquier parametrización suave de la línea mundial de la partícula. Si uno aplica el cálculo de las variaciones a esto, uno de nuevo obtiene las ecuaciones para una geodésica. Para simplificar los cálculos, primero se toma la variación del cuadrado del integrado. Para las métricas y coordenadas de este caso y suponiendo que la partícula se mueve en el plano ecuatorial Silencio Silencio =π π 2{textstyle theta ={frac {cHFF} } {2}}, ese cuadrado es

()cdτ τ dq)2=− − gμ μ.. dxμ μ dqdx.. dq=()1− − rsr)c2()dtdq)2− − 11− − rsr()drdq)2− − r2()dφ φ dq)2.{displaystyle left(c{frac {dtau }{dq}right)}{2}=-g_{mu} {fnMicroc {fnh00} ¿Qué? {fnMicrosoft Sans Serif} {fnMicroc} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicroc} {fnMicroc} {fnMicroc} {dt} {dq}right)}{2}-{frac {1} {1-{text{}}}}left({frac {dr}{dq}}right)}{2}-r^{2}left({frac {dvarphi }{dq}}}}}right)}{2},} {}}}} {}} {}} {}} {}} {}}} {}} {}}}}} {}}}}}} {} {}}} {}} {}}}}}}} {} {} {}}}}}} {}}} {} {}}}}}}}}}}}}}} {}}}}}}}} {}}}}} {}} {}}}}}}} {}}}}} {}}}}} {} {}}}}}}}}}}} {}}}}}}}}} {} {}}}}}}}}}}}}}}}}}}}}}}}}}} {

Tomando la variación de esto da

δ δ ()cdτ τ dq)2=2c2dτ τ dqδ δ dτ τ dq=δ δ [()1− − rsr)c2()dtdq)2− − 11− − rsr()drdq)2− − r2()dφ φ dq)2].{displaystyle delta left(c{frac {dtau}{dq}right)^{2}=2c^{2}{2}{frac {dtau } {dq}delta {fnMicroc {fnh} } {dq}=delta left[left(1-{text{}} {r}right)c^{2}left({fracfrac} {dt} {dq}right)}{2}-{frac {1} {1-{frac {f}}}}left({frac {dr}{dq}}right)}{2}-r^{2}left({frac {dvarphi }right)}{2}right]derecha],} {i}{2}}}}} {}{1}{1}}{1}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}} {

Moción en longitud

Vary con respecto a la longitud φ φ {textstyle varphi } sólo para conseguir

2c2dτ τ dqδ δ dτ τ dq=− − 2r2dφ φ dqδ δ dφ φ dq.{displaystyle 2c^{2}{frac {dtau } {dq}delta {fnMicroc {fnh} {fnK}=-2r^{2}{frac {dvarphi}{dq}delta #frac {dvarphi } {dq},.}

Divide by 2cdτ τ dq{textstyle 2c{frac {dtau } {dq}} para conseguir la variación del mismo componente

cδ δ dτ τ dq=− − r2cdφ φ dτ τ δ δ dφ φ dq=− − r2cdφ φ dτ τ dδ δ φ φ dq.{fnMicrosoft Sans Serif} {fnK} {f} {f} {f}} {f}} {f}} {f}} {f}} {f}} {f}} {f}}} {f}} {f} {f}}} {f} {f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnf}fnf}f}f}f}fnf}f}f}f}fnfnfnfnf}f}f}f}f}f}f}fn {dvarphi }{dtau }delta {fnMicroc {dvarphi } {dq}=-{frac {fnK} {fnMicroc}} {fnK}}} {fnMicroc}}} {f}}}} {fn}}} {f}}} {fn}}}}} {fn}}} {f}}} {f}}}}}}} {fnMicroc}}} {f}}}}}}}}}} {f}}}}}}} {f}}}}}} {f}}} {f}}}}} {f}}} {f} {f}}}}}}}}}}} {f}}}}}}} {f} {f} {f} {f} {f}}}}}}} {f} {f}}}f}}}}}}}}}}}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}} {dvarphi }{dtau }{frac {ddelta varphi } {dq},.}

Así

0=δ δ ∫ ∫ cdτ τ dqdq=∫ ∫ cδ δ dτ τ dqdq=∫ ∫ − − r2cdφ φ dτ τ dδ δ φ φ dqdq.{displaystyle 0=delta int {c{frac} {dtau ## {dq}dq}=int {cdelta {fnMicroc} {dtau ## {dq}dq}=int {fnMicroc {fnMicroc} {fnMicroc} {fnMicroc}} {fnMicroc}}} {fn}} {fnMicroc}}} {fnMicroc} {fn}}}} {f}} {fnMicroc}}}} {f}} {f}}}}}}}}}} {f}}}}}}}}} {f} {f} {f} {f} {dvarphi }{dtau }{frac {ddelta varphi {}dq}dq},}

La integración por partes da

0=− − r2cdφ φ dτ τ δ δ φ φ − − ∫ ∫ ddq[− − r2cdφ φ dτ τ ]δ δ φ φ dq.{displaystyle 0=-{frac}{c}{c}{frac}{frac} {f} {f} {f} {f}}}} {f}}}} {f}}} {f} {dvarphi }{dtau }delta varphi - 'int {{frac {d} {dq}left[-{frac} {fnK} {fnMicroc {dvarphi} {dtau}right]delta varphi dq},}

La variación de la longitud se supone que es cero en los puntos finales, por lo que el primer término desaparece. La integral se puede hacer sin cero por una opción perversa δ δ φ φ {textstyle delta varphi } a menos que el otro factor dentro sea cero en todas partes. Así que la ecuación del movimiento es

ddq[− − r2cdφ φ dτ τ ]=0.{displaystyle {frac {fnK}left {fnMicroc} {fnK} {fnMicroc}} {fnK}}} {fnMicroc}}} {f}}}} {fn}}} {f}}} {fn}}}}} {fn}}} {f}}} {f}}}}}}} {fnMicroc}}} {f}}}}}}}}}} {f}}}}}}} {f}}}}}} {f}}} {f}}}}} {f}}} {f} {f}}}}}}}}}}} {f}}}}}}} {f} {f} {f} {f} {f}}}}}}} {f} {f}}}f}}}}}}}}}}}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}} Vale.

Moción en el tiempo

Vary con respecto al tiempo t{textstyle t} sólo para conseguir

2c2dτ τ dqδ δ dτ τ dq=2()1− − rsr)c2dtdqδ δ dtdq.{displaystyle 2c^{2}{frac {dtau } {dq}delta {fnMicroc {fnh} ¿Qué? {dt}{dq}delta {fnMicroc {dt} {dq},}

Divide by 2cdτ τ dq{textstyle 2c{frac {dtau } {dq}} para conseguir la variación del mismo componente

cδ δ dτ τ dq=c()1− − rsr)dtdτ τ δ δ dtdq=c()1− − rsr)dtdτ τ dδ δ tdq.{displaystyle cdelta {frac {dtau {fnMicrosoft Sans Serif} {fnMicroc} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {dt}{dtau }delta {frac {dt}=cleft(1-{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}}}}} {f}}} {fnMicroc}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {dere} {dere} {r} {dere}}}}}} {r}}}}}}}}} {dere} {r}}}}}}}}}}}}}}}}}}}}}}}} {dere} {dere}}}}} {dere}}}}}}}}}}}}}}}}}}}} {dere}}}}} {dt}{dtau }{frac {ddelta.

Así

0=δ δ ∫ ∫ cdτ τ dqdq=∫ ∫ c()1− − rsr)dtdτ τ dδ δ tdqdq.{displaystyle 0=delta int {c{frac} {dtau {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}}}}}}derecha){frac} {dt}{dtau }{frac {ddelta.

La integración por partes da

0=c()1− − rsr)dtdτ τ δ δ t− − ∫ ∫ ddq[c()1− − rsr)dtdτ τ ]δ δ tdq.{displaystyle ¿Qué? {dt}{dtau }delta t-int {{frac} [cleft(1-{frac] Vale.

Entonces la ecuación del movimiento es

ddq[c()1− − rsr)dtdτ τ ]=0.{displaystyle {frac {}{dq}left[cleft(1-{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}}}}} {f}}} {fnMicroc}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {dere} {dere} {r} {dere}}}}}} {r}}}}}}}}} {dere} {r}}}}}}}}}}}}}}}}}}}}}}}} {dere} {dere}}}}} {dere}}}}}}}}}}}}}}}}}}}} {dere}}}}} {dt}{dtau }right]=0,}

Momenta conservada