G2 (matemáticas)

En matemáticas, G₂ es el nombre de tres grupos simples Lie (una forma compleja, una forma compacta real y una forma real dividida), sus álgebras Lie g2,{displaystyle {Mathfrak {}_{2} así como algunos grupos algebraicos. Son los más pequeños de los cinco grupos de mentira simple excepcional. G₂ tiene rango 2 y dimensión 14. Tiene dos representaciones fundamentales, con dimensión 7 y 14.

La forma compacta de G₂ puede describirse como el grupo de automorfismos del álgebra octonion o, de manera equivalente, como el subgrupo de SO(7) que conserva cualquier vector particular elegido en su dimensión 8 representación de espinor real (una representación de espín).

Historia

El álgebra de Lie g2{displaystyle {Mathfrak}_{2}, siendo el más pequeño excepcional simple Lie algebra, fue el primero de estos que se descubren en el intento de clasificar álgebras simple Lie. El 23 de mayo de 1887, Wilhelm Killing escribió una carta a Friedrich Engel diciendo que había encontrado un álgebra de mentira simple de 14 dimensiones, que ahora llamamos g2{displaystyle {Mathfrak}_{2}.

En 1893, Élie Cartan publicó una nota que describe un conjunto abierto C5{displaystyle mathbb {C} {5}} equipado con una distribución 2-dimensional—es decir, un campo suavemente variable de subespacios 2-dimensionales del espacio tangente—para el cual el álgebra de Lie g2{displaystyle {Mathfrak}_{2} aparece como las simetrías infinitesimal. En el mismo año, en la misma revista, Engel notó lo mismo. Más tarde se descubrió que la distribución 2-dimensional está estrechamente relacionada con una bola rodando en otra bola. El espacio de las configuraciones de la bola rodante es de 5 dimensiones, con una distribución de 2 dimensiones que describe los movimientos de la bola donde se roda sin deslizarse o girar.

En 1900, Engel descubrió que una forma trilineal antisimétrica genérica (o forma de 3) en un espacio vectorial complejo de 7 dimensiones se conserva mediante un grupo isomorfo a la forma compleja de G₂.

En 1908, Cartan mencionó que el grupo de automorfismos de los octoniones es un grupo de Lie simple de 14 dimensiones. En 1914 afirmó que esta es la forma real compacta de G₂.

En libros y artículos más antiguos, G₂ a veces se indica con E₂.

Formas reales

Hay 3 álgebras de Lie reales simples asociadas con este sistema raíz:

• El álgebra de Lie real subyacente del complejo Lie algebra G₂ tiene dimensión 28. Tiene una conjugación compleja como un automorfismo externo y simplemente está conectado. El subgrupo compacto maximal de su grupo asociado es la forma compacta de G₂.
• El álgebra de Lie de la forma compacta es de 14 dimensiones. El grupo asociado Lie no tiene automorfismos externos, ningún centro, y es simplemente conectado y compacto.
• El álgebra de Lie de la forma no-compact (split) tiene dimensión 14. El grupo asociado simple Lie tiene un grupo fundamental de orden 2 y su grupo de automorfismo externo es el grupo trivial. Su subgrupo compacto maximal es SU(2) × SU(2)/(1,−1). Tiene una cubierta doble no algebraica que está simplemente conectada.

Álgebra

Diagrama de Dynkin y matriz de Cartan

El diagrama de Dynkin para G₂ es dado por .

Su matriz de Cartan es:

[2− − 1− − 32]{displaystyle left[{begin{rr}{rr}2 limit-13 concluyen {array}right]}

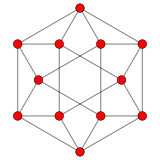
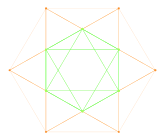
Raíces de G2

El sistema de raíz vectorial 12 de G2 en 2 dimensiones.

La A2 La proyección de plano de Coxeter de los 12 vértices del cuboctaedro contiene el mismo arreglo vectorial 2D.

Gráfico de G2 como subgrupo de F4 y E8 proyectado en el plano Coxeter

Aunque abarcan un espacio bidimensional, tal como están dibujados, es mucho más simétrico considerarlos como vectores en un subespacio bidimensional de un espacio tridimensional.

Un conjunto de raíces simples, para es:

(0,1,−1), (1,−2,1)

Grupo Weyl/Coxeter

Su grupo Weyl/Coxeter G=W()G2){displaystyle G=W(G_{2}} es el grupo dihedral D6{displaystyle D_{6} del orden 12. Tiene un grado mínimo fiel μ μ ()G)=5{displaystyle mu (G)=5}.

Holonomía especial

G₂ es uno de los posibles grupos especiales que pueden aparecer como grupo de holonomía de una métrica riemanniana. Las variedades de la holonomía G₂ también se denominan variedades G2.

Invariante polinomial

G₂ es el grupo de automorfismos de los siguientes dos polinomios en 7 variables no conmutativas.

C1=t2+u2+v2+w2+x2+Sí.2+z2{displaystyle C_{1}=t^{2}+u^{2}+v^{2}+w^{2}+x^{2}+y^{2}+z^{2}}

C2=tuv+wtx+Sí.wu+zSí.t+vzw+xvSí.+uxz{displaystyle C_{2}=tuv+wtx+ywu+zyt+vzw+xvy+uxz} (± permutaciones)

que proviene del álgebra octonion. Las variables deben ser no conmutativas, de lo contrario, el segundo polinomio sería idénticamente cero.

Generadores

Agregar una representación de los 14 generadores con coeficientes A,..., N da como resultado la matriz:

Aλ λ 1+⋯ ⋯ +Nλ λ 14=[0C− − BE− − D− − GF− − M− − C0AF− − G+ND− − K− − E− − LB− − A0− − NML− − K− − E− − FN0− − A+H− − B+IC− − JDG− − N− − MA− − H0JIGK− − D− − LB− − I− − J0− − H− − F+ME+LK− − C+J− − IH0]{displaystyle Alambda _{1}+cdots +Nlambda {14}={begin{bmatrix}0 ventaja-C correspond-E-LBcl-E-E-E-LE-M-M-C disminuye0 limitada-F sensible-G+N limitD-K implica-E-LB frecuentemente-E-E-E-B+D

Es exactamente el álgebra de Lie del grupo

G2={}g▪ ▪ SO()7):gAlternativa Alternativa φ φ =φ φ ,φ φ =⋅ ⋅ 123+⋅ ⋅ 145+⋅ ⋅ 167+⋅ ⋅ 246− − ⋅ ⋅ 257− − ⋅ ⋅ 347− − ⋅ ⋅ 356}{displaystyle G_{2}={gin SO(7):g^{*}varphi =varphivarphi =omega ^{123}+omega ^{145}+omega ^{167}+omega ^{246}-omega ^{257}-omega }

Representaciones

Los caracteres de las representaciones de dimensión finita de las álgebras de Lie reales y complejas y los grupos de Lie están dados por la fórmula de caracteres de Weyl. Las dimensiones de las representaciones irreducibles más pequeñas son (secuencia A104599 en el OEIS):

1, 7, 14, 27, 64, 77 (twice), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (twice), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (twice), 5005, 1305, 5103, 6630, 7293

La representación de 14 dimensiones es la representación adjunta, y la de 7 dimensiones es la acción de G₂ sobre los octoniones imaginarios.

Hay dos representaciones irreducibles no isomorfas de dimensiones 77, 2079, 4928, 30107, etc. Las representaciones fundamentales son las de dimensiones 14 y 7 (correspondientes a los dos nodos del diagrama de Dynkin en el orden tal que el triple puntas de flecha del primero al segundo).

Vogan (1994) describió las representaciones unitarias irreducibles (de dimensión infinita) de la forma real dividida de G₂.

Grupos finitos

El grupo G₂(q) son los puntos del grupo algebraico G₂ sobre el cuerpo finito F_q. Estos grupos finitos fueron introducidos por primera vez por Leonard Eugene Dickson en Dickson (1901) para q impares y Dickson (1905) para q pares. El orden de G₂(q) es q⁶(q⁶ − 1)(q² − 1). Cuando q ≠ 2, el grupo es simple, y cuando q = 2, tiene un subgrupo simple de índice 2 isomorfo a ²A₂(3²), y es el grupo de automorfismos de un orden máximo de los octoniones. El grupo Janko J1 se construyó primero como un subgrupo de G₂(11). Ree (1960) introdujo grupos de Ree retorcidos ²G₂(q) de orden q³(q³ + 1)(q − 1) para q = 3²ⁿ⁺¹, una potencia impar de 3.