Fusión nuclear

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

La fusión nuclear es una reacción en la que dos o más núcleos atómicos se combinan para formar uno o más núcleos atómicos diferentes y partículas subatómicas (neutrones o protones). La diferencia de masa entre los reactivos y los productos se manifiesta como liberación o absorción de energía. Esta diferencia de masa surge debido a la diferencia de energía de enlace nuclear entre los núcleos antes y después de la reacción. La fusión nuclear es el proceso que alimenta estrellas activas o de secuencia principal y otras estrellas de gran magnitud, donde se liberan grandes cantidades de energía.

Un proceso de fusión nuclear que produce núcleos atómicos más livianos que el hierro-56 o el níquel-62 generalmente liberará energía. Estos elementos tienen una masa relativamente pequeña y una energía de enlace relativamente grande por nucleón. La fusión de núcleos más livianos que estos libera energía (un proceso exotérmico), mientras que la fusión de núcleos más pesados resulta en energía retenida por los nucleones producto, y la reacción resultante es endotérmica. Lo contrario es cierto para el proceso inverso, llamado fisión nuclear. La fusión nuclear utiliza elementos más ligeros, como el hidrógeno y el helio, que en general son más fusibles; mientras que los elementos más pesados, como el uranio, el torio y el plutonio, son más fisionables. El evento astrofísico extremo de una supernova puede producir suficiente energía para fusionar núcleos en elementos más pesados que el hierro.

Historia

En 1920, Arthur Eddington sugirió que la fusión de hidrógeno y helio podría ser la principal fuente de energía estelar. Los túneles cuánticos fueron descubiertos por Friedrich Hund en 1929, y poco después Robert Atkinson y Fritz Houtermans utilizaron las masas medidas de elementos ligeros para demostrar que se podían liberar grandes cantidades de energía fusionando pequeños núcleos. Sobre la base de los primeros experimentos de transmutación nuclear artificial de Patrick Blackett, Mark Oliphant logró la fusión de laboratorio de isótopos de hidrógeno en 1932. En el resto de esa década, Hans Bethe elaboró la teoría del ciclo principal de fusión nuclear en estrellas.. La investigación sobre la fusión con fines militares comenzó a principios de la década de 1940 como parte del Proyecto Manhattan. La fusión nuclear autosostenida se llevó a cabo por primera vez el 1 de noviembre de 1952,

La investigación sobre el desarrollo de la fusión controlada dentro de los reactores de fusión ha estado en curso desde la década de 1940, pero la tecnología aún se encuentra en su fase de desarrollo.

Proceso

La liberación de energía con la fusión de elementos ligeros se debe a la interacción de dos fuerzas opuestas: la fuerza nuclear, que combina protones y neutrones, y la fuerza de Coulomb, que hace que los protones se repelan entre sí. Los protones tienen carga positiva y se repelen entre sí por la fuerza de Coulomb, pero aún así pueden permanecer juntos, lo que demuestra la existencia de otra fuerza de corto alcance denominada atracción nuclear.Los núcleos ligeros (o núcleos más pequeños que el hierro y el níquel) son lo suficientemente pequeños y pobres en protones, lo que permite que la fuerza nuclear supere la repulsión. Esto se debe a que el núcleo es lo suficientemente pequeño como para que todos los nucleones sientan la fuerza de atracción de corto alcance al menos con tanta fuerza como sienten la repulsión de Coulomb de alcance infinito. La formación de núcleos a partir de núcleos más ligeros por fusión libera la energía extra de la atracción neta de partículas. Sin embargo, para núcleos más grandes, no se libera energía, ya que la fuerza nuclear es de corto alcance y no puede continuar actuando en escalas de longitud nuclear más largas. Así, la energía no se libera con la fusión de tales núcleos; en cambio, se requiere energía como insumo para dichos procesos.

La fusión alimenta las estrellas y produce prácticamente todos los elementos en un proceso llamado nucleosíntesis. El Sol es una estrella de secuencia principal y, como tal, genera su energía mediante la fusión nuclear de núcleos de hidrógeno en helio. En su núcleo, el Sol fusiona 620 millones de toneladas métricas de hidrógeno y produce 616 millones de toneladas métricas de helio cada segundo. La fusión de elementos más ligeros en las estrellas libera energía y la masa que siempre la acompaña. Por ejemplo, en la fusión de dos núcleos de hidrógeno para formar helio, el 0,645 % de la masa se lleva en forma de energía cinética de una partícula alfa u otras formas de energía, como la radiación electromagnética.

Se necesita una energía considerable para forzar la fusión de los núcleos, incluso los del elemento más ligero, el hidrógeno. Cuando se aceleran a velocidades lo suficientemente altas, los núcleos pueden superar esta repulsión electrostática y acercarse lo suficiente como para que la fuerza nuclear atractiva sea mayor que la fuerza de Coulomb repulsiva. La fuerza fuerte crece rápidamente una vez que los núcleos están lo suficientemente cerca, y los nucleones que se fusionan pueden esencialmente "caer" entre sí y el resultado es la fusión y la energía neta producida. La fusión de núcleos más livianos, que crea un núcleo más pesado y, a menudo, un neutrón o protón libre, generalmente libera más energía de la que se necesita para forzar la unión de los núcleos; este es un proceso exotérmico que puede producir reacciones autosostenidas.

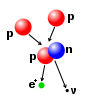
Energíaliberada en la mayoría de las reacciones nucleares es mucho mayor que en las reacciones químicas, porque la energía de enlace que mantiene unido un núcleo es mayor que la energía que mantiene los electrones en un núcleo. Por ejemplo, la energía de ionización obtenida al agregar un electrón a un núcleo de hidrógeno es13,6 eV: menos de una millonésima parte de la17,6 MeV liberados en la reacción de deuterio-tritio (D-T) que se muestra en el diagrama adyacente. Las reacciones de fusión tienen una densidad de energía muchas veces mayor que la fisión nuclear; las reacciones producen mucha más energía por unidad de masa, aunque las reacciones individuales de fisión son generalmente mucho más energéticas que las individuales de fusión, que son millones de veces más energéticas que las reacciones químicas. Solo la conversión directa de masa en energía, como la causada por la colisión aniquiladora de materia y antimateria, es más energética por unidad de masa que la fusión nuclear. (La conversión completa de un gramo de materia liberaría 9 × 10 julios de energía).

La investigación sobre el uso de la fusión para la producción de electricidad se ha llevado a cabo durante más de 60 años. Aunque la fusión controlada es generalmente manejable con la tecnología actual (por ejemplo, fusores), el logro exitoso de la fusión económica se ha visto obstaculizado por dificultades científicas y tecnológicas; no obstante, se han logrado avances importantes. En la actualidad, las reacciones de fusión controlada han sido incapaces de producir una fusión controlada de equilibrio (autosuficiente). Los dos enfoques más avanzados son el confinamiento magnético (diseños toroidales) y el confinamiento inercial (diseños láser).

Se están desarrollando diseños viables para un reactor toroidal que teóricamente entregará diez veces más energía de fusión que la cantidad necesaria para calentar el plasma a las temperaturas requeridas (ver ITER). Se espera que la instalación ITER finalice su fase de construcción en 2025. Comenzará a poner en marcha el reactor ese mismo año e iniciará los experimentos con plasma en 2025, pero no se espera que comience la fusión completa de deuterio-tritio hasta 2035.

De manera similar, General Fusion, con sede en Canadá, que está desarrollando un sistema de energía nuclear de fusión de objetivo magnetizado, tiene como objetivo construir su planta de demostración para 2025.

La Instalación Nacional de Ignición de EE. UU., que utiliza fusión por confinamiento inercial impulsada por láser, se diseñó con el objetivo de lograr una fusión sin pérdidas; los primeros experimentos con objetivos láser a gran escala se realizaron en junio de 2009 y los experimentos de encendido comenzaron a principios de 2011.

Fusión nuclear en estrellas

Un proceso de fusión importante es la nucleosíntesis estelar que alimenta a las estrellas, incluido el Sol. En el siglo XX, se reconoció que la energía liberada por las reacciones de fusión nuclear explica la longevidad del calor y la luz estelares. La fusión de núcleos en una estrella, a partir de su abundancia inicial de hidrógeno y helio, proporciona esa energía y sintetiza nuevos núcleos. Están involucradas diferentes cadenas de reacción, dependiendo de la masa de la estrella (y por lo tanto de la presión y temperatura en su núcleo).

Alrededor de 1920, Arthur Eddington anticipó el descubrimiento y el mecanismo de los procesos de fusión nuclear en las estrellas, en su artículo La constitución interna de las estrellas. En ese momento, la fuente de energía estelar era un completo misterio; Eddington especuló correctamente que la fuente fue la fusión de hidrógeno en helio, liberando una enorme energía según la ecuación de Einstein E = mc. Este fue un desarrollo particularmente notable ya que en ese momento aún no se había descubierto la fusión y la energía termonuclear, ni siquiera que las estrellas están compuestas en gran parte de hidrógeno (ver metalicidad). El artículo de Eddington razonó que:

La principal teoría de la energía estelar, la hipótesis de la contracción, debería hacer que la rotación de las estrellas se acelere visiblemente debido a la conservación del momento angular. Pero las observaciones de las estrellas variables Cefeidas mostraron que esto no estaba sucediendo.
La única otra fuente plausible de energía conocida era la conversión de materia en energía; Einstein había demostrado algunos años antes que una pequeña cantidad de materia equivalía a una gran cantidad de energía.
Francis Aston también había demostrado recientemente que la masa de un átomo de helio era aproximadamente un 0,8% menor que la masa de los cuatro átomos de hidrógeno que, combinados, formarían un átomo de helio (de acuerdo con la teoría de la estructura atómica prevaleciente en ese momento que mantenía el peso atómico ser la propiedad distintiva entre los elementos; el trabajo de Henry Moseley y Antonius van den Broek demostraría más tarde que la carga nucleica era la propiedad distintiva y que, por lo tanto, un núcleo de helio constaba de dos núcleos de hidrógeno más una masa adicional). Esto sugirió que si tal combinación pudiera ocurrir, liberaría una cantidad considerable de energía como subproducto.
Si una estrella contuviera solo un 5% de hidrógeno fusible, sería suficiente para explicar cómo las estrellas obtienen su energía. (Ahora sabemos que la mayoría de las estrellas 'ordinarias' contienen mucho más del 5% de hidrógeno).
También podrían fusionarse otros elementos, y otros científicos habían especulado que las estrellas eran el "crisol" en el que los elementos ligeros se combinaban para crear elementos pesados, pero sin mediciones más precisas de sus masas atómicas, no se podía decir nada más en ese momento.

Todas estas especulaciones demostraron ser correctas en las décadas siguientes.

La principal fuente de energía solar, y la de estrellas de tamaño similar, es la fusión de hidrógeno para formar helio (la reacción en cadena protón-protón), que se produce a una temperatura del núcleo solar de 14 millones de grados Kelvin. El resultado neto es la fusión de cuatro protones en una partícula alfa, con la liberación de dos positrones y dos neutrinos (que cambia dos de los protones en neutrones) y energía. En estrellas más pesadas, el ciclo CNO y otros procesos son más importantes. A medida que una estrella consume una fracción sustancial de su hidrógeno, comienza a sintetizar elementos más pesados. Los elementos más pesados se sintetizan por fusión que ocurre cuando una estrella más masiva sufre una supernova violenta al final de su vida, un proceso conocido como nucleosíntesis de supernova.

Requisitos

Se debe superar una barrera de energía sustancial de fuerzas electrostáticas antes de que pueda ocurrir la fusión. A grandes distancias, dos núcleos desnudos se repelen debido a la fuerza electrostática repulsiva entre sus protones cargados positivamente. Sin embargo, si dos núcleos pueden acercarse lo suficiente, la repulsión electrostática puede ser superada por el efecto cuántico en el que los núcleos pueden hacer un túnel a través de las fuerzas de culombio.

Cuando se agrega un nucleón, como un protón o un neutrón, a un núcleo, la fuerza nuclear lo atrae a todos los demás nucleones del núcleo (si el átomo es lo suficientemente pequeño), pero principalmente a sus vecinos inmediatos debido al corto alcance de la fuerza. Los nucleones en el interior de un núcleo tienen más nucleones vecinos que los de la superficie. Dado que los núcleos más pequeños tienen una mayor relación área superficial/volumen, la energía de enlace por nucleón debido a la fuerza nuclear generalmente aumenta con el tamaño del núcleo, pero se aproxima a un valor límite correspondiente al de un núcleo con un diámetro de aproximadamente cuatro nucleones. Es importante tener en cuenta que los nucleones son objetos cuánticos. Entonces, por ejemplo, dado que dos neutrones en un núcleo son idénticos entre sí, el objetivo de distinguir uno del otro,

La fuerza electrostática, por otro lado, es una fuerza de cuadrado inverso, por lo que un protón agregado a un núcleo sentirá una repulsión electrostática de todos los demás protones en el núcleo. La energía electrostática por nucleón debido a la fuerza electrostática aumenta sin límite a medida que crece el número atómico de los núcleos.

El resultado neto de la oposición de las fuerzas electroestática y nuclear fuerte es que la energía de enlace por nucleón generalmente aumenta al aumentar el tamaño, hasta los elementos hierro y níquel, y luego disminuye para los núcleos más pesados. Finalmente, la energía de enlace se vuelve negativa y los núcleos muy pesados (todos con más de 208 nucleones, que corresponden a un diámetro de unos 6 nucleones) no son estables. Los cuatro núcleos más unidos, en orden decreciente de energía de enlace por nucleón, sonNi,Fe,Fe, yNi. Aunque el isótopo de níquel,Ni, es más estable, el isótopo de hierroFees un orden de magnitud más común. Esto se debe al hecho de que no existe una manera fácil para que las estrellas creenNia través del proceso alfa.

Una excepción a esta tendencia general es el núcleo de helio-4, cuya energía de enlace es mayor que la del litio, el siguiente elemento más pesado. Esto se debe a que los protones y los neutrones son fermiones, que según el principio de exclusión de Pauli no pueden existir en el mismo núcleo exactamente en el mismo estado. El estado de energía de cada protón o neutrón en un núcleo puede acomodar tanto una partícula con giro hacia arriba como una partícula con giro hacia abajo. El helio-4 tiene una energía de enlace anómalamente grande porque su núcleo consta de dos protones y dos neutrones (es un núcleo doblemente mágico), por lo que sus cuatro nucleones pueden estar en el estado fundamental. Cualquier nucleon adicional tendria que pasar a estados de mayor energia. De hecho, el núcleo de helio-4 está tan estrechamente ligado que comúnmente se lo trata como una sola partícula mecánica cuántica en la física nuclear, es decir, la partícula alfa.

La situación es similar si se juntan dos núcleos. A medida que se acercan, todos los protones de un núcleo repelen a todos los protones del otro. Hasta que los dos núcleos no se acercan lo suficiente durante el tiempo suficiente para que la fuerza nuclear fuerte pueda hacerse cargo (a través de un túnel) no se supera la fuerza electrostática repulsiva. En consecuencia, incluso cuando el estado de energía final es más bajo, existe una gran barrera de energía que primero debe superarse. Se llama la barrera de Coulomb.

La barrera de Coulomb es la más pequeña para los isótopos de hidrógeno, ya que sus núcleos contienen una sola carga positiva. Un diprotón no es estable, por lo que los neutrones también deben estar involucrados, idealmente de tal manera que un núcleo de helio, con su unión extremadamente fuerte, sea uno de los productos.

Usando combustible de deuterio-tritio, la barrera de energía resultante es de aproximadamente 0,1 MeV. En comparación, la energía necesaria para extraer un electrón del hidrógeno es de 13,6 eV. El resultado (intermedio) de la fusión es un núcleo de He inestable, que inmediatamente expulsa un neutrón con 14,1 MeV. La energía de retroceso del núcleo de He restante es de 3,5 MeV, por lo que la energía total liberada es de 17,6 MeV. Esto es muchas veces más de lo que se necesitaba para superar la barrera energética.

La sección transversal de reacción (σ) es una medida de la probabilidad de una reacción de fusión en función de la velocidad relativa de los dos núcleos reactivos. Si los reactivos tienen una distribución de velocidades, por ejemplo, una distribución térmica, entonces es útil realizar un promedio de las distribuciones del producto de la sección transversal y la velocidad. Este promedio se denomina 'reactividad', denotado ⟨ σv ⟩. La velocidad de reacción (fusiones por volumen por tiempo) es ⟨ σv ⟩ veces el producto de las densidades numéricas de los reactivos: $f=n_{1}n_{2}langlesigma vrangle.$

Si una especie de núcleo reacciona con un núcleo como él mismo, como en la reacción DD, entonces el producto $n_{1}n_{2}$ debe ser reemplazado por $n^{2}/2$ .

$langle sigma vrangle$ aumenta desde prácticamente cero a temperatura ambiente hasta magnitudes significativas a temperaturas de 10 a 100 keV. A estas temperaturas, muy por encima de las energías de ionización típicas (13,6 eV en el caso del hidrógeno), los reactivos de fusión existen en estado de plasma.

La importancia de $langle sigma vrangle$ en función de la temperatura en un dispositivo con un determinado tiempo de confinamiento energético se encuentra considerando el criterio de Lawson. Esta es una barrera extremadamente difícil de superar en la Tierra, lo que explica por qué la investigación de la fusión ha tardado muchos años en alcanzar el estado técnico avanzado actual.

Fusión artificial

Fusión termonuclear

Si la materia se calienta lo suficiente (por lo tanto, es plasma) y está confinada, pueden ocurrir reacciones de fusión debido a colisiones con energías cinéticas térmicas extremas de las partículas. Las armas termonucleares producen lo que equivale a una liberación incontrolada de energía de fusión. Los conceptos de fusión termonuclear controlada utilizan campos magnéticos para confinar el plasma.

Fusión por confinamiento inercial

La fusión por confinamiento inercial (ICF) es un método destinado a liberar energía de fusión calentando y comprimiendo un objetivo de combustible, generalmente una pastilla que contiene deuterio y tritio.

Confinamiento electrostático inercial

El confinamiento electrostático inercial es un conjunto de dispositivos que utilizan un campo eléctrico para calentar iones a condiciones de fusión. El más conocido es el fusor. A partir de 1999, varios aficionados han podido realizar fusiones amateur utilizando estos dispositivos caseros. Otros dispositivos IEC incluyen: los conceptos Polywell, MIX POPS y Marble.

Fusión haz-haz o haz-objetivo

La fusión de iones ligeros basada en aceleradores es una técnica que utiliza aceleradores de partículas para lograr energías cinéticas de partículas suficientes para inducir reacciones de fusión de iones ligeros. Acelerar iones ligeros es relativamente fácil y se puede hacer de manera eficiente, ya que solo requiere un tubo de vacío, un par de electrodos y un transformador de alto voltaje; la fusión se puede observar con tan solo 10 kV entre los electrodos. El sistema se puede configurar para acelerar iones en un objetivo infundido con combustible estático, conocido como fusión haz-objetivo, o acelerando dos flujos de iones uno hacia el otro, fusión haz-haz.

El problema clave con la fusión basada en aceleradores (y con objetivos fríos en general) es que las secciones transversales de fusión son muchos órdenes de magnitud más bajas que las secciones transversales de interacción de Coulomb. Por lo tanto, la gran mayoría de los iones gastan su energía emitiendo radiación bremsstrahlung y la ionización de los átomos del objetivo. Los dispositivos denominados generadores de neutrones de tubo sellado son particularmente relevantes para esta discusión. Estos pequeños dispositivos son aceleradores de partículas en miniatura llenos de gas de deuterio y tritio en una disposición que permite que los iones de esos núcleos se aceleren contra objetivos de hidruro, que también contienen deuterio y tritio, donde tiene lugar la fusión, liberando un flujo de neutrones.

A lo largo de los años se han realizado varios intentos de recircular los iones que "pierden" las colisiones. Uno de los intentos más conocidos en la década de 1970 fue Migma, que utilizó un anillo de almacenamiento de partículas único para capturar iones en órbitas circulares y devolverlos al área de reacción. Los cálculos teóricos realizados durante las revisiones de financiación señalaron que el sistema tendría grandes dificultades para crecer y contener suficiente combustible de fusión para ser relevante como fuente de energía. En la década de 1990, Norman Rostoker propuso una nueva disposición que utilizaba una configuración de campo inverso (FRC) como sistema de almacenamiento y TAE Technologies continúa estudiándola a partir de 2021. Un enfoque estrechamente relacionado es fusionar dos FRC que giran en direcciones opuestas,que está siendo estudiado activamente por Helion Energy. Debido a que todos estos enfoques tienen energías de iones mucho más allá de la barrera de Coulomb, a menudo sugieren el uso de ciclos de combustible alternativos como pB que son demasiado difíciles de intentar con enfoques convencionales.

Fusión catalizada por muones

La fusión catalizada por muones es un proceso de fusión que ocurre a temperaturas ordinarias. Fue estudiado en detalle por Steven Jones a principios de la década de 1980. La producción de energía neta de esta reacción no ha tenido éxito debido a la alta energía requerida para crear muones, su corta vida media de 2,2 µs y la alta probabilidad de que un muón se una a la nueva partícula alfa y, por lo tanto, deje de catalizar la fusión.

Otros principios

Se han investigado algunos otros principios de confinamiento.

La fusión inicializada con antimateria utiliza pequeñas cantidades de antimateria para desencadenar una pequeña explosión de fusión. Esto se ha estudiado principalmente en el contexto de hacer factibles la propulsión de pulsos nucleares y las bombas de fusión pura. Esto no está cerca de convertirse en una fuente de energía práctica, debido solo al costo de fabricación de antimateria.
La fusión piroeléctrica fue reportada en abril de 2005 por un equipo de la UCLA. Los científicos utilizaron un cristal piroeléctrico calentado de -34 a 7 °C (-29 a 45 °F), combinado con una aguja de tungsteno para producir un campo eléctrico de aproximadamente 25 gigavoltios por metro para ionizar y acelerar los núcleos de deuterio en un objetivo de deuteruro de erbio.. A los niveles de energía estimados, puede ocurrir la reacción de fusión DD, produciendo helio-3 y un neutrón de 2,45 MeV. Aunque es un generador de neutrones útil, el aparato no está destinado a la generación de energía ya que requiere mucha más energía de la que produce. Se han observado reacciones de fusión de DT con un objetivo de erbio tritiado.
La fusión-fisión nuclear híbrida (energía nuclear híbrida) es un medio propuesto para generar energía mediante el uso de una combinación de procesos de fusión y fisión nuclear. El concepto data de la década de 1950 y fue defendido brevemente por Hans Bethe durante la década de 1970, pero permaneció en gran medida sin explorar hasta un resurgimiento del interés en 2009, debido a los retrasos en la realización de la fusión pura.
El Proyecto PACER, llevado a cabo en el Laboratorio Nacional de Los Álamos (LANL) a mediados de la década de 1970, exploró la posibilidad de un sistema de energía de fusión que implicaría la explosión de pequeñas bombas de hidrógeno (bombas de fusión) dentro de una cavidad subterránea. Como fuente de energía, el sistema es el único sistema de energía de fusión que se pudo demostrar que funciona con la tecnología existente. Sin embargo, también requeriría un gran suministro continuo de bombas nucleares, lo que hace que la economía de dicho sistema sea bastante cuestionable.
La fusión de burbujas, también llamada sonofusión, fue un mecanismo propuesto para lograr la fusión a través de la cavitación sónica que saltó a la fama a principios de la década de 2000. Los intentos posteriores de replicación fracasaron y el investigador principal, Rusi Taleyarkhan, fue declarado culpable de mala conducta en la investigación en 2008.

Reacciones importantes

Cadenas de reacciones estelares

A las temperaturas y densidades de los núcleos estelares, las velocidades de las reacciones de fusión son notoriamente lentas. Por ejemplo, a la temperatura del núcleo solar (T ≈ 15 MK) y densidad (160 g/cm), la tasa de liberación de energía es de solo 276 μW/cm, aproximadamente una cuarta parte de la tasa volumétrica a la que un cuerpo humano en reposo genera calor. Por lo tanto, la reproducción de las condiciones del núcleo estelar en un laboratorio para la producción de energía de fusión nuclear es completamente impracticable. Debido a que las tasas de reacción nuclear dependen tanto de la densidad como de la temperatura y la mayoría de los esquemas de fusión operan a densidades relativamente bajas, esos métodos dependen en gran medida de temperaturas más altas. La velocidad de fusión en función de la temperatura (exp(− E / kT)), conduce a la necesidad de alcanzar temperaturas en los reactores terrestres de 10 a 100 veces mayores que en los interiores estelares: T ≈ 0.1–1.0×10 K.

Criterios y candidatos para reacciones terrestres

En la fusión artificial, el combustible primario no está obligado a ser protones y se pueden usar temperaturas más altas, por lo que se eligen reacciones con secciones transversales más grandes. Otra preocupación es la producción de neutrones, que activan radiológicamente la estructura del reactor, pero también tienen la ventaja de permitir la extracción volumétrica de la energía de fusión y la crianza de tritio. Las reacciones que no liberan neutrones se denominan aneutrónicas.

Para ser una fuente de energía útil, una reacción de fusión debe satisfacer varios criterios. Debería:ser exotérmicoEsto limita los reactivos al lado bajo Z (número de protones) de la curva de energía de enlace. También hace helio.Élel producto más común debido a su unión extraordinariamente apretada, aunqueÉlyHtambién aparece.Involucran núcleos de bajo número atómico (Z)Esto se debe a que la repulsión electrostática que debe superarse antes de que los núcleos estén lo suficientemente cerca para fusionarse está directamente relacionada con la cantidad de protones que contiene: su número atómico.tiene dos reactivosEn densidades inferiores a las estelares, las colisiones de tres cuerpos son demasiado improbables. En el confinamiento inercial, tanto las densidades estelares como las temperaturas se superan para compensar las deficiencias del tercer parámetro del criterio de Lawson, el tiempo de confinamiento muy corto de ICF.Tener dos o más productos.Esto permite la conservación simultánea de la energía y el impulso sin depender de la fuerza electromagnética.Conservar protones y neutrones.Las secciones transversales para la interacción débil son demasiado pequeñas.

Pocas reacciones cumplen estos criterios. Los siguientes son los de mayores secciones transversales:

(1)

₁D

₁T

→

₂Él

(

3,52 MeV

)

norte

(

14,06 MeV

)

(2i)

₁D

→

₁T

(

1,01 MeV

)

pag

(

3,02 MeV

)

50%

(2ii)

→

₂Él

(

0,82 MeV

)

norte

(

2,45 MeV

)

50%

(3)

₁D

₂Él

→

₂Él

(

3,6 MeV

)

pag

(

14,7 MeV

)

(4)

₁T

→

₂Él

2 norte

11,3 MeV

(5)

₂Él

→

₂Él

12,9 MeV

(6i)

₂Él

₁T

→

₂Él

pag

norte

12,1 MeV

57%

(6ii)

→

₂Él

(

4,8 MeV

)

₁D

(

9,5 MeV

)

43%

(7i)

₁D

₃li

→

2 ₂Él

22,4 MeV

(7ii)

→

₂Él

norte

2,56 MeV

(7iii)

→

₃li

pag

5,0 MeV

(7iv)

→

₄Ser

norte

3,4 MeV

(8)

pag

₃li

→

₂Él

(

1,7 MeV

)

₂Él

(

2,3 MeV

)

(9)

₂Él

₃li

→

2 ₂Él

pag

16,9 MeV

(10)

pag

₅B

→

3 ₂Él

8,7 MeV

Nucleosíntesis

Nucleosíntesis estelarNucleosíntesis del Big BangNucleosíntesis de supernovasEspalación de rayos cósmicos
Temas relacionados
AstrofísicaFusión nuclearproceso RS-procesoFisión nuclear
vtmi

Para reacciones con dos productos, la energía se divide entre ellos en proporción inversa a sus masas, como se muestra. En la mayoría de las reacciones con tres productos, la distribución de energía varía. Para reacciones que pueden dar como resultado más de un conjunto de productos, se dan las proporciones de ramificación.

Algunos candidatos a reacción se pueden eliminar de una vez. La reacción D- Li no tiene ninguna ventaja en comparación con p-₅Bporque es más o menos tan difícil de quemar pero produce sustancialmente más neutrones a través de₁D-₁Dreacciones secundarias. También hay una p-₃lipero la sección transversal es demasiado baja, excepto posiblemente cuando Ti > ₁ MeV, pero a temperaturas tan altas una reacción endotérmica productora de neutrones directos también se vuelve muy significativa. Finalmente también hay un p-₄Serreacción, que no sólo es difícil de quemar, sino₄Serpuede inducirse fácilmente a dividirse en dos partículas alfa y un neutrón.

Además de las reacciones de fusión, las siguientes reacciones con neutrones son importantes para "criar" tritio en bombas de fusión "secas" y algunos reactores de fusión propuestos:

norte	+	₃li	→	₁T	+	₂Él+ 4,784 MeV
norte	+	₃li	→	₁T	+	₂Él+ n – 2,467 MeV

La última de las dos ecuaciones se desconocía cuando EE. UU. llevó a cabo la prueba de la bomba de fusión Castle Bravo en 1954. Siendo solo la segunda bomba de fusión jamás probada (y la primera en usar litio), los diseñadores de Castle Bravo "Shrimp" habían entendido la utilidad del Li en la producción de tritio, pero no había reconocido que la fisión del Li aumentaría en gran medida el rendimiento de la bomba. Mientras que Li tiene una pequeña sección transversal de neutrones para bajas energías de neutrones, tiene una sección transversal más alta por encima de 5 MeV. El rendimiento de 15 Mt fue un 250 % mayor que el previsto de 6 Mt y provocó una exposición inesperada a la lluvia radiactiva.

Para evaluar la utilidad de estas reacciones, además de los reactivos, los productos y la energía liberada, se necesita saber algo sobre la sección transversal nuclear. Cualquier dispositivo de fusión dado tiene una presión de plasma máxima que puede soportar, y un dispositivo económico siempre operaría cerca de este máximo. Dada esta presión, la mayor salida de fusión se obtiene cuando la temperatura se elige de modo que ⟨ σv ⟩/ T sea un máximo. Esta es también la temperatura a la que el valor del triple producto nTτ requerido para la ignición es mínimo, ya que ese valor requerido es inversamente proporcional a ⟨ σv ⟩/ T(ver criterio de Lawson). (Un plasma se "encende" si las reacciones de fusión producen suficiente energía para mantener la temperatura sin calentamiento externo). Esta temperatura óptima y el valor de ⟨ σv ⟩/ T a esa temperatura se dan para algunas de estas reacciones en la siguiente tabla.

Gasolina	T [keV]	⟨ σv ⟩/ T [m /s/keV ]
₁D-₁T	13.6	1.24×10
₁D-₁D	15	1.28×10
₁D-₂Él	58	2.24×10
pag- _₃li	66	1.46×10
pag- _₅B	123	3.01×10

Tenga en cuenta que muchas de las reacciones forman cadenas. Por ejemplo, un reactor alimentado con₁Ty₂Élcrea algunos₁D, que luego es posible utilizar en el₁D-₂Élreacción si las energías son "correctas". Una idea elegante es combinar las reacciones (8) y (9). Él₂Élde la reacción (8) puede reaccionar con₃lien la reacción (9) antes de termalizar completamente. Esto produce un protón energético, que a su vez sufre la reacción (8) antes de termalizarse. Un análisis detallado muestra que esta idea no funcionaría bien, pero es un buen ejemplo de un caso en el que la suposición habitual de un plasma maxwelliano no es apropiada.

Neutronicidad, requisito de confinamiento y densidad de potencia

Cualquiera de las reacciones anteriores puede, en principio, ser la base de la producción de energía de fusión. Además de la temperatura y la sección transversal discutidas anteriormente, debemos considerar la energía total de los productos de fusión E _fus, la energía de los productos de fusión cargados E _ch y el número atómico Z del reactivo no hidrogénico.

Especificación de la₁D-₁DSin embargo, la reacción conlleva algunas dificultades. Para empezar, se debe promediar sobre las dos ramas (2i) y (2ii). Más difícil es decidir cómo tratar el₁Ty₂Élproductos₁Tarde tan bien en un plasma de deuterio que es casi imposible extraerlo del plasma. Él₁D-₂ÉlLa reacción se optimiza a una temperatura mucho más alta, por lo que el quemado en el punto óptimo₁D-₁Dla temperatura puede ser baja. Por lo tanto, parece razonable suponer que la₁Tpero no el₂Élse quema y agrega su energía a la reacción neta, lo que significa que la reacción total sería la suma de (2i), (2ii) y (1):5₁D→₂Él+ 2 norte +₂Él+ p, E _fus = 4,03+17,6+3,27 = 24,9 MeV, E _ch = 4,03+3,5+0,82 = 8,35 MeV.

Para calcular la potencia de un reactor (en el que la velocidad de reacción está determinada por el paso DD), contamos el₁D-₁Denergía de fusión por reacción DD como E _fus = (4,03 MeV + 17,6 MeV) × 50 % + (3,27 MeV) × 50 % = 12,5 MeV y la energía en partículas cargadas como E _ch = (4,03 MeV + 3,5 MeV) × 50 % + (0,82 MeV) × 50 % = 4,2 MeV. (Nota: si el ion tritio reacciona con un deuterón mientras todavía tiene una gran energía cinética, entonces la energía cinética del helio-4 producido puede ser bastante diferente de 3,5 MeV, por lo que este cálculo de energía en partículas cargadas es solo una aproximación del promedio.) La cantidad de energía consumida por deuterón es 2/5 de esto, o 5.0 MeV (una energía específica de alrededor de 225 millones de MJ por kilogramo de deuterio).

Otro aspecto único de la₁D-₁Dreacción es que solo hay un reactivo, que debe tenerse en cuenta al calcular la velocidad de reacción.

Con esta elección, tabulamos parámetros para cuatro de las reacciones más importantes.

Gasolina	Z	E _fus [MeV]	E _ch [MeV]	neutronicidad
₁D-₁T	1	17.6	3.5	0.80
₁D-₁D	1	12.5	4.2	0,66
₁D-₂Él	2	18.3	18.3	≈0.05
pag- _₅B	5	8.7	8.7	≈0.001

La última columna es la neutronicidad de la reacción, la fracción de la energía de fusión liberada como neutrones. Este es un indicador importante de la magnitud de los problemas asociados con los neutrones, como el daño por radiación, el blindaje biológico, el manejo remoto y la seguridad. Para las dos primeras reacciones se calcula como (E _fus - E _ch)/ E _fus. Para las dos últimas reacciones, en las que este cálculo daría cero, los valores citados son estimaciones aproximadas basadas en reacciones secundarias que producen neutrones en un plasma en equilibrio térmico.

Por supuesto, los reactivos también deben mezclarse en las proporciones óptimas. Este es el caso cuando cada ion reactivo más sus electrones asociados representan la mitad de la presión. Suponiendo que la presión total sea fija, esto significa que la densidad de partículas del ion no hidrogénico es menor que la del ion hidrogenado por un factor de 2/(Z +1). Por lo tanto, la velocidad de estas reacciones se reduce por el mismo factor, además de cualquier diferencia en los valores de ⟨ σv ⟩/ T. Por otra parte, porque el₁D-₁Dreacción tiene un solo reactivo, su velocidad es el doble que cuando el combustible se divide entre dos especies hidrogenadas diferentes, creando así una reacción más eficiente.

Por lo tanto, existe una "penalización" de (2/(Z +1)) para los combustibles no hidrogénicos que surge del hecho de que requieren más electrones, que toman presión sin participar en la reacción de fusión. (Por lo general, es una buena suposición que la temperatura de los electrones será casi igual a la temperatura de los iones. Sin embargo, algunos autores discuten la posibilidad de que los electrones puedan mantenerse sustancialmente más fríos que los iones. En tal caso, conocido como "caliente"). modo de iones", la "penalización" no se aplicaría.) Al mismo tiempo, hay una "bonificación" de un factor 2 para₁D-₁Dporque cada ion puede reaccionar con cualquiera de los otros iones, no solo con una fracción de ellos.

Ahora podemos comparar estas reacciones en la siguiente tabla.

Gasolina	⟨ σv ⟩/ T	penalización/bonificación	reactividad inversa	criterio de Lawson	densidad de potencia (W/m /kPa)	relación inversa de la densidad de potencia
₁D-₁T	1.24×10	1	1	1	34	1
₁D-₁D	1.28×10	2	48	30	0.5	68
₁D-₂Él	2.24×10	2/3	83	dieciséis	0.43	80
pag- _₃li	1.46×10	1/2	1700		0.005	6800
pag- _₅B	3.01×10	1/3	1240	500	0.014	2500

El valor máximo de ⟨ σv ⟩/ T se toma de una tabla anterior. El factor de "penalización/bonificación" es el relacionado con un reactivo no hidrogénico o una reacción de una sola especie. Los valores de la columna "reactividad inversa" se obtienen dividiendo 1,24 × 10 por el producto de la segunda y la tercera columna. Indica el factor por el cual las otras reacciones ocurren más lentamente que la₁D-₁Treacción en condiciones comparables. La columna "Criterio de Lawson" pondera estos resultados con E _ch y da una indicación de cuánto más difícil es lograr la ignición con estas reacciones, en relación con la dificultad para el₁D-₁Treacción. La penúltima columna está etiquetada como "densidad de potencia" y pondera la reactividad práctica por E _fus. La columna final indica cuánto menor es la densidad de potencia de fusión de las otras reacciones en comparación con la₁D-₁Treacción y puede considerarse una medida del potencial económico.

Pérdidas por bremsstrahlung en plasmas isotrópicos casi neutros

Los iones que experimentan la fusión en muchos sistemas esencialmente nunca ocurrirán solos, sino que se mezclarán con electrones que, en conjunto, neutralizarán la carga eléctrica principal de los iones y formarán un plasma. Los electrones generalmente tendrán una temperatura comparable o mayor que la de los iones, por lo que colisionarán con los iones y emitirán radiación de rayos X de 10 a 30 keV de energía, un proceso conocido como Bremsstrahlung.

El enorme tamaño del Sol y las estrellas significa que los rayos X producidos en este proceso no escaparán y depositarán su energía de nuevo en el plasma. Se dice que son opacos a los rayos X. Pero cualquier reactor de fusión terrestre será ópticamente delgado para rayos X de este rango de energía. Los rayos X son difíciles de reflejar, pero se absorben eficazmente (y se convierten en calor) en acero inoxidable de menos de mm de espesor (que forma parte del escudo del reactor). Esto significa que el proceso de bremsstrahlung extrae energía del plasma y lo enfría.

La relación entre la potencia de fusión producida y la radiación de rayos X que se pierde en las paredes es una figura de mérito importante. Esta relación generalmente se maximiza a una temperatura mucho más alta que la que maximiza la densidad de potencia (consulte la subsección anterior). La siguiente tabla muestra estimaciones de la temperatura óptima y la relación de potencia a esa temperatura para varias reacciones:

Gasolina	Ti ₍ keV)	P _fusion / P _{Bremsstrahlung}
₁D-₁T	50	140
₁D-₁D	500	2.9
₁D-₂Él	100	5.3
₂Él-₂Él	1000	0.72
pag- _₃li	800	0.21
pag- _₅B	300	0.57

Las proporciones reales de potencia de fusión a Bremsstrahlung probablemente serán significativamente más bajas por varias razones. Por un lado, el cálculo supone que la energía de los productos de fusión se transmite completamente a los iones de combustible, que luego pierden energía a los electrones por colisiones, que a su vez pierden energía por Bremsstrahlung. Sin embargo, debido a que los productos de fusión se mueven mucho más rápido que los iones de combustible, cederán una fracción significativa de su energía directamente a los electrones. En segundo lugar, se supone que los iones del plasma son puramente iones de combustible. En la práctica, habrá una proporción significativa de iones de impurezas, que luego reducirán la proporción. En particular, los propios productos de fusión deben permanecer en el plasma hasta que hayan perdido su energía, ypermanecer durante algún tiempo después de eso en cualquier esquema de confinamiento propuesto. Finalmente, se han ignorado todos los canales de pérdida de energía que no sean Bremsstrahlung. Los dos últimos factores están relacionados. En términos teóricos y experimentales, el confinamiento de partículas y energía parecen estar estrechamente relacionados. En un esquema de confinamiento que retiene bien la energía, se acumularán productos de fusión. Si los productos de fusión se expulsan de manera eficiente, el confinamiento de energía también será deficiente.

Las temperaturas que maximizan la potencia de fusión en comparación con la Bremsstrahlung son en todos los casos superiores a la temperatura que maximiza la densidad de potencia y minimiza el valor requerido del triple producto de fusión. Esto no cambiará el punto de operación óptimo para₁D-₁Tmucho porque la fracción Bremsstrahlung es baja, pero empujará a los otros combustibles a regímenes donde la densidad de potencia relativa a₁D-₁Tes aún menor y el confinamiento requerido aún más difícil de lograr. Para₁D-₁Dy₁D-₂Él, las pérdidas de Bremsstrahlung serán un problema grave, posiblemente prohibitivo. Para₂Él-₂Él, pag-₃liy P-₅Blas pérdidas de Bremsstrahlung parecen hacer imposible un reactor de fusión que utilice estos combustibles con un plasma isotrópico casi neutro. Se han considerado algunas formas de salir de este dilema, pero se han rechazado. Esta limitación no se aplica a los plasmas no neutros y anisotrópicos; sin embargo, estos tienen sus propios desafíos a los que enfrentarse.

Descripción matemática de la sección transversal

Fusión bajo la física clásica

En una imagen clásica, los núcleos pueden entenderse como esferas duras que se repelen entre sí a través de la fuerza de Coulomb pero se fusionan una vez que las dos esferas se acercan lo suficiente para hacer contacto. Estimando el radio de un núcleo atómico como un femtómetro, la energía necesaria para la fusión de dos hidrógenos es: [{text{2 protones}}]}}{frac {1}{4pi epsilon _{0}}}{frac {e^{2}}{1 {ce { fm}}}}aprox. 1,4 {ce {MeV}}}">

Esto implicaría que para el núcleo del sol, que tiene una distribución de Boltzmann con una temperatura de alrededor de 1,4 keV, la probabilidad de que el hidrógeno alcance el umbral es ${ estilo de visualización 10^{-290}}$ , es decir, la fusión nunca ocurriría. Sin embargo, la fusión en el sol ocurre debido a la mecánica cuántica.

Parametrización de la sección transversal

La probabilidad de que se produzca la fusión aumenta considerablemente en comparación con la imagen clásica, gracias a la difusión del radio efectivo como la longitud de onda de DeBroglie, así como al efecto túnel cuántico a través de la barrera de potencial. Para determinar la velocidad de las reacciones de fusión, el valor de mayor interés es la sección transversal, que describe la probabilidad de que las partículas se fusionen dando un área característica de interacción. Una estimación del área de la sección transversal de fusión a menudo se divide en tres partes: ${ estilo de visualización sigma aproximadamente sigma _ {geometría} veces T veces R}$

Donde ${ estilo de visualización sigma _ {geometría}}$ es la sección transversal geométrica, T es la transparencia de la barrera y R son las características de reacción de la reacción.

${ estilo de visualización sigma _ {geometría}}$ es del orden del cuadrado de la longitud de onda de De-Broglie ${displaystyle sigma_{geometría}approx lambda ^{2}={bigg (}{frac {hbar }{m_{r}v}}{bigg)}^{2}propto { frac{1}{épsilon}}}$ donde ${ estilo de visualización m_ {r}}$ es la masa reducida del sistema y $epsilon$ es el centro de energía de masa del sistema.

R contiene toda la física nuclear de la reacción específica y toma valores muy diferentes dependiendo de la naturaleza de la interacción. Sin embargo, para la mayoría de las reacciones, la variación de ${ Displaystyle R ( épsilon)}$ es pequeño en comparación con la variación del factor de Gamow y, por lo tanto, se aproxima mediante una función llamada factor S astrofísico, ${ estilo de visualización S ( épsilon)}$ , que varía débilmente en energía. Juntando estas dependencias, una aproximación para la sección transversal de fusión en función de la energía toma la forma: ${displaystyle sigma (epsilon)approx {frac {S(epsilon)}{epsilon }}e^{-{sqrt {epsilon _{G}/epsilon }}}}$

Se pueden derivar formas más detalladas de la sección transversal a través de modelos basados en la física nuclear y la teoría de la matriz R.

Fórmulas de secciones transversales de fusión

El formulario de física de plasma del Laboratorio de Investigación Naval proporciona la sección transversal total en graneros en función de la energía (en keV) de la partícula incidente hacia un ion objetivo en reposo ajustado por la fórmula: ${displaystyle sigma ^{text{NRL}}(epsilon)={frac {A_{5}+{big (}(A_{4}-A_{3}epsilon)^{2}+ 1{grande)}^{-1}A_{2}}{epsilon (e^{A_{1}epsilon ^{-1/2}}-1)}}}$ con los siguientes valores de coeficiente:

	DT(1)	DD(2i)	DD(2ii)	DH (3)	TT(4)	el (6)
A1	45.95	46.097	47.88	89.27	38.39	123.1
A2	50200	372	482	25900	448	11250
A3	1.368 × 10	4,36 × 10	3,08 × 10	3,98 × 10	1.02 × 10	0
A4	1.076	1.22	1.177	1.297	2.09	0
A5	409	0	0	647	0	0

Bosch-Hale también informa sobre secciones transversales calculadas con matriz R que ajustan los datos de observación con los coeficientes de aproximación racional de Padé. Con energía en unidades de keV y secciones transversales en unidades de milibarn, el factor tiene la forma: ${displaystyle S^{text{Bosch-Hale}}(epsilon)={frac {A_{1}+epsilon {bigg (}A_{2}+epsilon {big (}A_{3) }+epsilon (A_{4}+epsilon A_{5}){grande)}{bigg)}}{1+epsilon {bigg (}B_{1}+epsilon {grande (} B_{2}+epsilon (B_{3}+epsilon B_{4}){grande)}{grande)}}}}$ , con los valores del coeficiente:

{displaystyle (Delta S)_{text{máximo}}%}

	DT(1)	DD(2ii)	DH (3)	La
$epsilon _{G}$	31.3970	68.7508	31.3970	34.3827
A1	5.5576 × 10	5.7501 × 10	5.3701 × 10	6.927 × 10
A2	2.1054 × 10	2.5226 × 10	3.3027 × 10	7.454 × 10
A3	−3,2638 × 10	4.5566 × 10	−1,2706 × 10	2.050 × 10
A4	1.4987 × 10	0	2.9327 × 10	5.2002 × 10
A5	1.8181 × 10	0	−2,5151 × 10	0
B1	0	−3,1995 × 10	0	6,38 × 10
B2	0	−8,5530 × 10	0	−9,95 × 10
B3	0	5.9014 × 10	0	6.981 × 10
B4	0	0	0	1.728 × 10
Rango de energía aplicable [keV]	0.5-5000	0.3-900	0.5-4900	0.5-550
${displaystyle (Delta S)_{text{máximo}}%}$	2.0	2.2	2.5	1.9

donde ${displaystyle sigma ^{text{Bosch-Hale}}(epsilon)={frac {S^{text{Bosch-Hale}}(epsilon)}{epsilon exp(epsilon_{ G}/{sqrt {epsilon}})}}}$

Secciones transversales nucleares promediadas por Maxwell

En los sistemas de fusión que están en equilibrio térmico, las partículas están en una distribución de Maxwell-Boltzmann, lo que significa que las partículas tienen un rango de energías centradas alrededor de la temperatura del plasma. El sol, los plasmas confinados magnéticamente y los sistemas de fusión por confinamiento inercial están bien modelados para estar en equilibrio térmico. En estos casos, el valor de interés es la sección transversal de fusión promediada en la distribución de Maxwell-Boltzmann. El formulario de física de plasma del Laboratorio de Investigación Naval tabula las reactividades de las secciones transversales de fusión promediadas de Maxwell en ${displaystyle mathrm {cm^{3}/seg} }$ .

Temperatura [keV]	DT(1)	DD(2ii)	DH (3)	TT(4)	el (6)
1	5,5 × 10	1,5 × 10	1.0 × 10	3,3 × 10	1.0 × 10
2	2,6 × 10	5,4 × 10	1,4 × 10	7,1 × 10	1.0 × 10
5	1,3 × 10	1,8 × 10	6,7 × 10	1,4 × 10	2,1 × 10
10	1,1 × 10	1,2 × 10	2,3 × 10	7,2 × 10	1,2 × 10
20	4,2 × 10	5,2 × 10	3,8 × 10	2,5 × 10	2,6 × 10
50	8,7 × 10	2,1 × 10	5,4 × 10	8,7 × 10	5,3 × 10
100	8,5 × 10	4,5 × 10	1,6 × 10	1,9 × 10	2,7 × 10
200	6,3 × 10	8,8 × 10	2,4 × 10	4,2 × 10	9,2 × 10
500	3,7 × 10	1,8 × 10	2,3 × 10	8,4 × 10	2,9 × 10
1000	2,7 × 10	2,2 × 10	1,8 × 10	8.0 × 10	5,2 × 10

con T en unidades de keV.

Contenido relacionado

Más resultados...