Funtores adjuntos
En matemáticas, específicamente en teoría de categorías, adjunción es una relación que pueden exhibir dos funtores, lo que intuitivamente corresponde a una forma débil de equivalencia entre dos categorías relacionadas. Dos funtores que se encuentran en esta relación se conocen como funtores adjuntos, siendo uno el adjunto izquierdo y el otro el adjunto derecho. Los pares de funtores adjuntos son omnipresentes en matemáticas y, a menudo, surgen de construcciones de "soluciones óptimas" a ciertos problemas (es decir, construcciones de objetos que tienen una cierta propiedad universal), como la construcción de un grupo libre en un conjunto en álgebra, o la construcción de la compactación de Stone-Čech de un espacio topológico en topología.
Por definición, una disposición entre categorías C{displaystyle {fnMithcal}} y D{displaystyle {fnMithcal}} es un par de functores (según sea covariante)
- F:D→ → C{displaystyle F: {fnMitcal {fnMitcal {fnMitcal} {C}} y G:C→ → D{displaystyle G:{mathcal {C}derecho {fnK}
y, para todos los objetos X{displaystyle X} dentro C{displaystyle {fnMithcal}} y Y{displaystyle Sí. dentro D{displaystyle {fnMithcal}} una bijeción entre los respectivos conjuntos de morfismo
- homC()FY,X).. homD()Y,GX){displaystyle mathrm {hom} _{mathcal {C}(FY,X)cong mathrm {hom} _{mathcal {D}(Y,GX)}
tal que esta familia de bijeones es natural en X{displaystyle X} y Y{displaystyle Sí.. Naturalidad aquí significa que hay isomorfismos naturales entre el par de functores C()F− − ,X):D→ → Set{displaystyle {mathcal {}(F-,X):{mathcal {D}to mathrm {Set} y D()− − ,GX):D→ → Set{displaystyle {mathcal {}(-,GX):{mathcal {D}to mathrm {Set} para un fijo X{displaystyle X} dentro C{displaystyle {fnMithcal}}, y también el par de functores C()FY,− − ):C→ → Set{displaystyle {mathcal {}(FY,-):{mathcal {C}to mathrm {Set} y D()Y,G− − ):C→ → Set{displaystyle {mathcal {}(Y,G-):{mathcal {C}to mathrm {Set} para un fijo Y{displaystyle Sí. dentro D{displaystyle {fnMithcal}}.
El functor F{displaystyle F} se llama izquierda functor adjunto o a la izquierda G{displaystyle G., mientras G{displaystyle G. se llama derecho junte functor o derecho a F{displaystyle F}.
An adjunction between categories C{displaystyle {fnMithcal}} y D{displaystyle {fnMithcal}} es algo similar a una "forma débil" de una equivalencia entre C{displaystyle {fnMithcal}} y D{displaystyle {fnMithcal}}, y de hecho cada equivalencia es una adjunción. En muchas situaciones, una adjunción puede ser "acelerada" a una equivalencia, por una adecuada modificación natural de las categorías involucradas y los functores.
Terminología y notación
Los términos adjunto y adjunto se utilizan y son cognados: uno se toma directamente del latín, el otro del latín a través del francés. En el texto clásico Categorías para el matemático que trabaja, Mac Lane hace una distinción entre los dos. Dada una familia
- φ φ XY:homC()FY,X).. homD()Y,GX){displaystyle varphi _{XY}:mathrm {hom} _{mathcal {C}(FY,X)cong mathrm {hom} _{mathcal {D}(Y,GX)}
de las bijetillas hom-set, llamamos φ φ {displaystyle varphi } an adjunción o un adjunción entre F{displaystyle F} y G{displaystyle G.. Si f{displaystyle f} es una flecha en homC()FY,X){displaystyle mathrm {hom} _{mathcal {C}(FY,X)}, φ φ f{displaystyle varphi f} es la derecha adjunct de f{displaystyle f} (pág. 81). El functor F{displaystyle F} es izquierda a G{displaystyle G., y G{displaystyle G. es derecho a F{displaystyle F}. (Nota eso) G{displaystyle G. puede tener una unión derecha que es bastante diferente de F{displaystyle F}; véase a continuación un ejemplo.)
En general, las frases "F{displaystyle F} es un conjunto izquierdo y "F{displaystyle F} tiene un derecho unido" son equivalentes. Llamamos F{displaystyle F} una unión izquierda porque se aplica al argumento izquierdo homC{displaystyle mathrm {hom} _{mathcal {C}}, y G{displaystyle G. un derecho unido porque se aplica al argumento correcto homD{displaystyle mathrm {hom} _{mathcal {}}.
Si F se deja junto a G, también escribimos
- F⊣ ⊣ G.{displaystyle Fdashv G.}
La terminología proviene de la idea espacial de Hilbert de operadores adjuntos T{displaystyle T}, U{displaystyle U} con .. TSí.,x.. =.. Sí.,Ux.. {displaystyle langle Ty,xrangle =langle y,Uxrangle }, que es formalmente similar a la relación anterior entre hom-sets. La analogía con los mapas adjuntos de los espacios de Hilbert se puede hacer precisa en ciertos contextos.
Introducción y Motivación
El lema es "Los funerarios unidos surgen por todas partes".
—Saunders Mac Lane, Categorías para el Trabajo Matemático
Con mucha frecuencia, las construcciones matemáticas comunes son funtores adjuntos. En consecuencia, los teoremas generales sobre los funtores adjuntos izquierdo/derecho codifican los detalles de muchos resultados útiles y no triviales. Dichos teoremas generales incluyen la equivalencia de las diversas definiciones de funtores adjuntos, la unicidad de un adjunto derecho para un adjunto izquierdo dado, el hecho de que los funtores adjuntos izquierdo/derecho conservan respectivamente colimits/límites (que también se encuentran en todas las áreas de las matemáticas), y los teoremas generales del funtor adjunto que dan condiciones bajo las cuales un funtor dado es un adjunto izquierdo/derecho.
Soluciones a problemas de optimización
En cierto sentido, un funtor adjunto es una forma de dar la solución más eficiente a algún problema a través de un método que es formulaico. Por ejemplo, un problema elemental en la teoría de anillos es cómo convertir un anillo (que es como un anillo que podría no tener una identidad multiplicativa) en un anillo. La forma más eficiente es adjuntar un elemento '1' al rng, unir todos (y solo) los elementos que son necesarios para satisfacer los axiomas del anillo (por ejemplo, r+1 para cada r en el anillo), y no imponer relaciones en el anillo recién formado que no están forzadas por axiomas. Además, esta construcción es formulaica en el sentido de que funciona esencialmente de la misma manera para cualquier rng.
Esto es bastante vago, aunque sugerente, y se puede precisar en el lenguaje de la teoría de categorías: una construcción es más eficiente si satisface una propiedad universal y es formulaica si define un funtor. Las propiedades universales vienen en dos tipos: propiedades iniciales y propiedades terminales. Dado que se trata de nociones duales, sólo es necesario discutir una de ellas.
La idea de usar una propiedad inicial es plantear el problema en términos de alguna categoría auxiliar E, de modo que el problema en cuestión corresponda a encontrar un objeto inicial de E. Esto tiene la ventaja de que la optimización—la sensación de que el proceso encuentra la solución más eficiente—significa algo riguroso y reconocible, algo así como el logro de un supremum. La categoría E también es formulaica en esta construcción, ya que siempre es la categoría de elementos del funtor al que se le está construyendo un adjunto.
Volvamos a nuestro ejemplo: tome el rng R dado y cree una categoría E cuyos objetos sean homomorfismos rng R → S, con S un anillo que tiene una identidad multiplicativa. Los morfismos en E entre R → S1 y R → S2 son triángulos conmutativos de la forma (R → S1, R → S2, S1 → S 2) donde S1 → S2 es un mapa circular (que preserva la identidad). (Tenga en cuenta que esta es precisamente la definición de la categoría de coma de R sobre la inclusión de anillos unitarios en rng). La existencia de un morfismo entre R → S 1 y R → S2 implica que S1 es una solución al menos tan eficiente como S2 para nuestro problema: S2 puede tener más elementos adjuntos y/o más relaciones no impuestas por axiomas que S1. Por tanto, la afirmación de que un objeto R → R* es inicial en E, es decir, que hay un morfismo de él a cualquier otro elemento de E, significa que el anillo R* es una solución más eficiente a nuestro problema.
Los dos hechos de que este método de convertir anillos en anillos es más eficiente y formulaico se pueden expresar simultáneamente diciendo que define un funtor adjunto. Más explícitamente: Deje que F denote el proceso anterior de adjuntar una identidad a un rng, entonces F(R)=R*. Sea G el proceso de "olvidar" si un anillo S tiene una identidad y considerarlo simplemente como un anillo, por lo que esencialmente G(S)=S. Entonces F es el funtor adjunto izquierdo de G.
Sin embargo, tenga en cuenta que todavía no hemos construido R*; es un hecho algebraico importante y no del todo trivial que tal funtor adjunto izquierdo R → R* realmente existe.
Simetría de problemas de optimización
También es posible comenzar con el funtor F, y plantear la siguiente (vaga) pregunta: ¿hay algún problema al que F es la solución más eficiente?
La noción de que F es la solución más eficiente al problema planteado por G es, en cierto sentido riguroso, equivalente a la noción de que G plantea el problema más difícil que resuelve F.
Esto da la intuición detrás del hecho de que los funtores adjuntos ocurren en pares: si F se deja adjunto a G, entonces G es correcto adjunto a F.
Definiciones formales
Hay varias definiciones equivalentes para los funtores adjuntos:
- Las definiciones a través de los morfismos universales son fáciles de indicar, y requieren verificaciones mínimas al construir un functor adjunto o probar dos functores son unidos. También son los más análogos a nuestra intuición que implica optimizaciones.
- La definición a través de conjuntos de homo hace la simetría más evidente, y es la razón para usar la palabra adjoint.
- La definición a través de counit-unit adjunction es conveniente para las pruebas sobre los functores que se sabe que están unidos, porque proporcionan fórmulas que pueden ser manipuladas directamente.
La equivalencia de estas definiciones es bastante útil. Los funtores adjuntos surgen en todas partes, en todas las áreas de las matemáticas. Dado que la estructura de cualquiera de estas definiciones da lugar a las estructuras de las demás, el cambio entre ellas hace uso implícito de muchos detalles que, de otro modo, tendrían que repetirse por separado en cada área temática.
Convenios
La teoría de los adjuntos tiene los términos izquierda y derecha en su base, y hay muchos componentes que viven en una de dos categorías C y D que están bajo consideración. Por lo tanto, puede ser útil elegir las letras en orden alfabético de acuerdo a si viven en la "izquierda" categoría C o la "derecha" categoría D, y también anotarlas en este orden siempre que sea posible.
En este artículo, por ejemplo, las letras X, F, f, ε denotarán consistentemente cosas que viven en la categoría C, las letras Y, G, g, η denotarán consistentemente cosas que viven en la categoría D , y siempre que sea posible se hará referencia a tales cosas en orden de izquierda a derecha (un funtor F: D → C puede ser considerado como "viviendo" donde están sus salidas, en C).
Definición mediante morfismos universales
Por definición, un functor F:D→ → C{displaystyle F:Dto C} es un izquierda functor adjunto si para cada objeto X{displaystyle X} dentro C{displaystyle C} existe un morfismo universal desde F{displaystyle F} a X{displaystyle X}. Expulsado, esto significa que para cada objeto X{displaystyle X} dentro C{displaystyle C} existe un objeto G()X){displaystyle G(X)} dentro D{displaystyle D} y un morfismo ε ε X:F()G()X))→ → X{displaystyle epsilon _{X}:F(G(X))to X} tal que por cada objeto Y{displaystyle Sí. dentro D{displaystyle D} y todo morfismo f:F()Y)→ → X{displaystyle f:F(Y)to X} existe un morfismo único g:Y→ → G()X){displaystyle g:Yto G(X)} con ε ε X∘ ∘ F()g)=f{displaystyle epsilon _{X}circ F(g)=f}.
La última ecuación se expresa mediante el siguiente diagrama conmutativo:
En esta situación, se puede demostrar que G{displaystyle G. se puede convertir en un functor G:C→ → D{displaystyle G:Cto D} de una manera única ε ε X∘ ∘ F()G()f))=f∘ ∘ ε ε X.{displaystyle epsilon _{X}circ F(G(f))=fcirc epsilon _{X'} para todos los morfismos f:X.→ → X{displaystyle f:X'to X} dentro C{displaystyle C}; F{displaystyle F} entonces se llama izquierda a G{displaystyle G..
Del mismo modo, podemos definir functores de unión derecha. Un functor G:C→ → D{displaystyle G:Cto D} es un derecho junte functor si para cada objeto Y{displaystyle Sí. dentro D{displaystyle D}, existe un morfismo universal Y{displaystyle Sí. a G{displaystyle G.. Expulsado, esto significa que para cada objeto Y{displaystyle Sí. dentro D{displaystyle D}, existe un objeto F()Y){displaystyle F(Y)} dentro C{displaystyle C} y un morfismo .. Y:Y→ → G()F()Y)){displaystyle eta - Sí. tal que por cada objeto X{displaystyle X} dentro C{displaystyle C} y todo morfismo g:Y→ → G()X){displaystyle g:Yto G(X)} existe un morfismo único f:F()Y)→ → X{displaystyle f:F(Y)to X} con G()f)∘ ∘ .. Y=g{displaystyle G(f)circ eta ¿Qué?.
Otra vez, esto F{displaystyle F} se puede convertir en un functor único F:D→ → C{displaystyle F:Dto C} tales que G()F()g))∘ ∘ .. Y=.. Y.∘ ∘ g{displaystyle G(F(g)circeta eta ¿Qué? ¿Qué? para g:Y→ → Y.{displaystyle g:Yto Y} un morfismo en D{displaystyle D}; G{displaystyle G. entonces se llama derecho a F{displaystyle F}.
Es verdad, como la terminología implica, que F{displaystyle F} está a la izquierda G{displaystyle G. si G{displaystyle G. es derecho a F{displaystyle F}.
Estas definiciones a través de morfismos universales a menudo son útiles para establecer que un funtor dado es adjunto a la izquierda o a la derecha, porque son minimalistas en sus requisitos. También son intuitivamente significativos en el sentido de que encontrar un morfismo universal es como resolver un problema de optimización.
Definición a través de complemento Hom-set
Una adjunción hom-set entre dos categorías C y D consta de dos funtores F: D → C y G: C → D y un isomorfismo natural
- CCPR CCPR :homC()F− − ,− − )→ → homD()− − ,G− − ){displaystyle Phi:mathrm {hom} _{C}(F-,-)to mathrm {hom} _{D}(-,G-)}.
Esto especifica una familia de biyecciones
- CCPR CCPR Y,X:homC()FY,X)→ → homD()Y,GX){displaystyle Phi _{Y,X}:mathrm {hom} _{C}(FY,X)to mathrm {hom} - Sí.
para todos los objetos X en C e Y en D.
En esta situación, F se deja junto a G y G se encuentra junto a la derecha F .
Esta definición es un compromiso lógico en el sentido de que es más difícil de satisfacer que las definiciones de morfismos universales y tiene menos implicaciones inmediatas que la definición de unidad-país. Es útil debido a su obvia simetría y como un trampolín entre las otras definiciones.
Para interpretar Φ como un isomorfismo natural, se debe reconocer homC(F–, –) y homD(–, G –) como funtores. De hecho, ambos son bifuntores de Dop × C a Set (la categoría de conjuntos). Para obtener más detalles, consulte el artículo sobre los funtores hom. Explícitamente, la naturalidad de Φ significa que para todos los morfismos f: X → X′ en C y todos los morfismos g: Y′ → Y en D el siguiente diagrama conmuta:
Las flechas verticales en este diagrama son las inducidas por la composición. Formalmente, Hom(Fg, f): HomC(FY, X) → HomC(FY′, X′) viene dado por h → f o h o Fg para cada h en HomC(FY, X). Hom(g, Gf) es similar.
Definición a través de la adjunción de unidad-país
Una adjunción de unidad-país entre dos categorías C y D consta de dos funtores F: D → C y G: C → D y dos transformaciones naturales
- ε ε :FG→ → 1C.. :1D→ → GF{displaystyle {begin{aligned}varepsilon:FGto 1_{mathcal {C}\eta >=mathcal {D}to GFend{aligned}}} {f}}} {f}\fnMicrosoft {f}}}}}}} {b}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\b9}b9b9}b9}b9}b9}b9}b9}b9}b9}}b}b9}}b}b9}b9}b9}b}}}}b9}}}}b9}b}}b9}}}}}}}}}}}}}}}}
llamados respectivamente el counit y la unidad de la adjunción (terminología del álgebra universal), tales que las composiciones
- F→F.. FGF→ε ε FF{displaystyle F{xrightarrow {;Feta FGF{xrightarrow {;varepsilon F,}F}
- G→.. GGFG→Gε ε G{displaystyle G{xrightarrow {;eta G. {;Gvarepsilon ¿Qué?
son las transformaciones de identidad 1F y 1G en F y G respectivamente.
En esta situación decimos que F está a la izquierda G y G es derecho a F , y puede indicar esta relación por escrito()ε ε ,.. ):F⊣ ⊣ G{displaystyle (varepsiloneta): Fdashv G}, o simplementeF⊣ ⊣ G{displaystyle Fdashv G}.
En forma de ecuación, las condiciones anteriores en (ε,η) son las ecuaciones counit-unit
- 1F=ε ε F∘ ∘ F.. 1G=Gε ε ∘ ∘ .. G{displaystyle {begin{aligned}1_{F} Fcirc Feta \1_{G} circ eta Gend{aligned}}
lo que significa que para cada X en C y cada Y en D,
- 1FY=ε ε FY∘ ∘ F().. Y)1GX=G()ε ε X)∘ ∘ .. GX{displaystyle {begin{aligned}1_{FY} ################################################################################################################################################################################################################################################################ ¿Por qué? ¿Por qué? ¿Qué?.
Note que 1C{displaystyle 1_{Mathcal {C}} denota el functor identificador en la categoría C{displaystyle {fnMithcal}}, 1F{displaystyle 1_{F} denota la identidad transformación natural del functor F a sí mismo, y 1FY{displaystyle 1_{FY} denota el morfismo de identidad del objeto FY.
Estas ecuaciones son útiles para reducir las pruebas sobre los functores adjuntos a las manipulaciones algebraicas. A veces se les llama identidades triángulo, o a veces el ecuaciones zig-zag por la apariencia de los diagramas de cuerda correspondientes. Una manera de recordarlos es escribir primero la ecuación no sensorial 1=ε ε ∘ ∘ .. {displaystyle 1=varepsilon circ eta } y luego rellenar F o G en una de las dos formas simples que hacen las composiciones definidas.
Nota: El uso del prefijo "co" in counit aquí no es consistente con la terminología de límites y colimits, porque un colimit satisface una propiedad inicial mientras que los morfismos counit satisfarán propiedades terminales, y dualmente. El término unidad aquí se toma prestado de la teoría de las mónadas donde parece la inserción de la identidad 1 en un monoide.
Historia
La idea de los funtores adjuntos fue presentada por Daniel Kan en 1958. Como muchos de los conceptos de la teoría de categorías, fue sugerida por las necesidades del álgebra homológica, que en ese momento estaba dedicada a los cálculos. Aquellos que se enfrentaron a hacer presentaciones ordenadas y sistemáticas del tema habrían notado relaciones tales como
- hom(F()X), Y*X, G()Y)
en la categoría de grupos abelianos, donde F era el functor − − ⊗ ⊗ A{displaystyle -otimes A} (es decir, tomar el producto tensor con A), y G fue el hondurista homA,–) (esto se conoce ahora como la adjunción de tensor-hom). El uso del iguales señal es un abuso de notación; esos dos grupos no son realmente idénticos, pero hay una manera de identificarlos que es naturales naturales. Se puede considerar natural sobre la base, en primer lugar, de que se trata de dos descripciones alternativas de los mapas bilineales de X × A a Y. Eso es, sin embargo, algo particular en el caso del producto tensor. En la teoría de la categoría la 'naturalidad' de la bijeción se subsume en el concepto de un isomorfismo natural.
Ubicuidad
Si uno comienza a buscar estos pares de funtores adjuntos, resultan ser muy comunes en el álgebra abstracta, y también en otros lugares. La siguiente sección de ejemplo proporciona evidencia de esto; además, las construcciones universales, que pueden ser más familiares para algunos, dan lugar a numerosos pares de funtores adjuntos.
De acuerdo con el pensamiento de Saunders Mac Lane, cualquier idea, como los funtores adjuntos, que aparece con suficiente frecuencia en matemáticas debe estudiarse por sí misma.
Los conceptos se pueden juzgar según su uso para resolver problemas, así como para su uso en la construcción de teorías. La tensión entre estas dos motivaciones fue especialmente grande durante la década de 1950, cuando se desarrolló inicialmente la teoría de categorías. Ingrese a Alexander Grothendieck, quien usó la teoría de categorías para orientarse en otros trabajos: en análisis funcional, álgebra homológica y, finalmente, geometría algebraica.
Probablemente sea incorrecto decir que promovió el concepto de funtor adjunto de forma aislada: pero el reconocimiento del papel de la adjunción era inherente al enfoque de Grothendieck. Por ejemplo, uno de sus mayores logros fue la formulación de la dualidad de Serre en forma relativa, en forma libre, en una familia continua de variedades algebraicas. Toda la prueba giraba en torno a la existencia de un derecho adjunto a cierto funtor. Esto es algo innegablemente abstracto y no constructivo, pero también poderoso a su manera.
Ejemplos
Grupos gratuitos
La construcción de grupos libres es un ejemplo común e ilustrativo.
Sea F: Set → Grp el funtor que asigna a cada conjunto Y el grupo libre generado por los elementos de Y, y sea G: Grp → Set el funtor olvidadizo, que asigna a cada grupo X su conjunto subyacente. Entonces F se deja adjunto a G:
Morfismos iniciales. Para cada conjunto Y, el conjunto GFY es sólo el conjunto subyacente del grupo libre FY generados por Y. Vamos.. Y:Y→ → GFY{displaystyle eta Y a GFYsea el mapa establecido dado por "inclusión de generadores". Este es un morfismo inicial Y a G, porque cualquier mapa de conjunto Y al conjunto subyacente GW de algún grupo W factor a través.. Y:Y→ → GFY{displaystyle eta Y a GFYa través de un homomorfismo de grupo único FY a W. Esta es precisamente la propiedad universal del grupo libre sobre Y.
Morfismos terminales. Para cada grupo X, el grupo FGX es el grupo libre generado libremente por GX, los elementos de X. Vamosε ε X:FGX→ → X{displaystyle varepsilon _{X}:FGXto X}ser el homomorfismo de grupo que envía los generadores de FGX a los elementos de X corresponden a, que existe por la propiedad universal de grupos libres. Entonces cada uno()GX,ε ε X){displaystyle (GX,varepsilon _{X})}es un morfismo terminal de F a X, porque cualquier homomorfismo grupo de un grupo libre FZ a X factor a travésε ε X:FGX→ → X{displaystyle varepsilon _{X}:FGXto X}a través de un mapa de conjunto único Z a GX. Esto significa que...F,GEs un par de adjoint.
Adjunción de conjunto hom. Los homomorfismos de grupo del grupo libre FY a un grupo X corresponden precisamente a mapas del conjunto Y al conjunto GX: cada homomorfismo de FY a X está totalmente determinado por su acción sobre los generadores, otra reformulación del propiedad universal de los grupos libres. Se puede verificar directamente que esta correspondencia es una transformación natural, lo que significa que es una adjunción hom-set para el par (F,G).
counit-unit adjunction. También se puede verificar directamente que ε y pira son naturales. Entonces, una verificación directa de que forman una adjunción de unidad de counidad()ε ε ,.. ):F⊣ ⊣ G{displaystyle (varepsiloneta): Fdashv G}es el siguiente:
La primera ecuación de unidad 1F=ε ε F∘ ∘ F.. {displaystyle 1_{F}=varepsilon Fcirc Feta }dice que para cada set Y la composición
- FY→F().. Y)FGFY→ε ε FYFY{displaystyle FY{xrightarrow {;F(eta FGFY{xrightarrow {;varepsilon - Sí.
debería ser la identidad. El grupo intermedio FGFY es el grupo libre generado libremente por las palabras del grupo libre FY. (Piensa en estas palabras como colocado entre paréntesis para indicar que son generadores independientes.) La flechaF().. Y){displaystyle F(eta - Sí.es el homomorfismo del grupo FY en FGFY enviar cada generador Sí. de FY a la palabra correspondiente de la longitud uno (Sí.) como un generador de FGFY. La flechaε ε FY{displaystyle varepsilon _{FY}es el homomorfismo del grupo FGFY a FY enviar cada generador a la palabra FY corresponde a (así que este mapa es "trayendo paréntesis"). La composición de estos mapas es de hecho la identidad en FY.
La segunda ecuación de unidad 1G=Gε ε ∘ ∘ .. G{displaystyle 1_{G}=Gvarepsilon circ eta G}dice que para cada grupo X la composición
- GX→.. GXGFGX→G()ε ε X)GX{displaystyle GX{xrightarrow {; GFGX{xrightarrow {;G(varepsilon _{X}}} GX}
debería ser la identidad. El conjunto intermedio GFGX es sólo el conjunto subyacente de FGX. La flecha.. GX{displaystyle eta _{GX}es el mapa conjunto "inclusión de generadores" del conjunto GX al conjunto GFGX. La flechaG()ε ε X){displaystyle G(varepsilon ¿Qué?es el mapa conjunto de GFGX a GX que subyace al homomorfismo grupo enviando cada generador de FGX al elemento X Corresponde a ("traer paréntesis"). La composición de estos mapas es de hecho la identidad en GX.
Construcciones libres y funtores olvidadizos
Todos los objetos libres son ejemplos de un adjunto izquierdo a un funtor olvidadizo que asigna a un objeto algebraico su conjunto subyacente. Estos funtores libres algebraicos tienen generalmente la misma descripción que en la descripción detallada de la situación de grupo libre anterior.
Funtores diagonales y límites
Los productos, los productos de fibra, los ecualizadores y los núcleos son ejemplos de la noción categórica de límite. Cualquier funtor límite es adjunto a la derecha de un funtor diagonal correspondiente (siempre que la categoría tenga el tipo de límites en cuestión), y la counidad de la adjunción proporciona los mapas de definición del objeto límite (es decir, del funtor diagonal en el límite, en el categoría de funtores). A continuación se muestran algunos ejemplos específicos.
- Productos Dejar izar: Grp2 → Grp el functor que asigna a cada par (X1, X2) el grupo de productos X1×X2, y dejar Δ: Grp → Grp2 ser el functor diagonal que asigna a cada grupo X el par (X, X) en la categoría del producto Grp2. La propiedad universal del grupo de productos muestra que ♥ es derecho-adjoint a Δ. La counidad de esta adjunción es el par de definir mapas de proyección de X1×X2 a X1 y X2 que define el límite, y la unidad es el inclusión diagonal de un grupo X en X×X (mapping x to (x,x)).
- El producto cartesiano de los conjuntos, el producto de los anillos, el producto de los espacios topológicos etc. siguen el mismo patrón; también se puede extender de manera sencilla a más de dos factores. Más generalmente, cualquier tipo de límite es adecuado para un functor diagonal.
- Kernels. Considerar la categoría D homomorfismos de grupos abelianos. Si f1: A1 → B1 y f2: A2 → B2 son dos objetos de D, entonces un morfismo de f1 a f2 es un par (gA, gB) de los morfismos tal que gBf1 = f2gA. Vamos G: D → Ab ser el functor que asigna a cada homomorfismo su núcleo y dejar F: Ab → D ser el functor que mapea el grupo A al homomorfismo A → Entonces G es derecho a F, que expresa la propiedad universal de los núcleos. La counidad de esta adjunción es la definición de la incrustación del núcleo de un homomorfismo en el dominio del homomorfismo, y la unidad es el morfismo que identifica a un grupo A con el núcleo del homomorfismo A → 0.
- Una variación adecuada de este ejemplo también muestra que los functores del núcleo para espacios vectoriales y para módulos son complementos adecuados. Análogamente, se puede demostrar que los functores de cokernel para grupos abelianos, espacios vectoriales y módulos quedan unidos.
Colímites y funtores diagonales
Los coproductos, los coproductos fibrosos, los coecualizadores y los conúcleos son ejemplos de la noción categórica de colímite. Cualquier funtor colimit se deja adjunto a un funtor diagonal correspondiente (siempre que la categoría tenga el tipo de colimits en cuestión), y la unidad de la adjunción proporciona los mapas de definición en el objeto colimit. A continuación se muestran algunos ejemplos específicos.
- Coproductos. Si F: Ab2 → Ab asigna a cada par (X1, X2) de los grupos abelianos su suma directa, y si G: Ab → Ab2 es el functor que asigna a cada grupo abeliano Y el par (Y, Y), entonces F está a la izquierda G, nuevamente una consecuencia de la propiedad universal de sumas directas. La unidad de este par de adjoint es el par de definir mapas de inclusión de X1 y X2 en la suma directa, y la counidad es el mapa aditivo de la suma directa de (X,X) a volver a X (sentir un elemento (a,b) de la suma directa al elemento a+b de X).
- Ejemplos analógicos son dados por la suma directa de espacios y módulos vectoriales, por el producto libre de grupos y por la unión de conjuntos.
Más ejemplos
Álgebra
- Adjuntar una identidad a un rng. Este ejemplo fue discutido en la sección de motivación anterior. Dado un rng R, un elemento de identidad multiplicativo se puede añadir tomando RxZ y definir un Z- producto bilineal con (r,0)(0,1) = (0,1)(r,0) = (r,0), (r,0)(s,0) = (rs,0), (0,1)(0,1) = (0,1). Esto construye una unión izquierda al funerario tomando un anillo al rin subyacente.
- Adjuntar una identidad a un semigrupo. Del mismo modo, dado un semigrupo S, podemos añadir un elemento de identidad y obtener un monoide tomando el sindicato descomunal S ⊔ ⊔ {displaystyle sqcup } {1} y la definición de una operación binaria en ella de tal manera que extiende la operación en S y 1 es un elemento de identidad. Esta construcción da a un funerario que es una unión izquierda al funerario tomando un monoide al semigrupo subyacente.
- Extensiones de anillo. Suppose R y S son anillos, y ρ: R → S es un homomorfismo de anillo. Entonces... S se puede ver como un (izquierda) R-modulo, y el producto tensor con S rinde un functor F: R-Mod → S-Mod. Entonces... F se deja junto al funerario olvidadizo G: S-Mod → R-Mod.
- Productos de tensor. Si R es un anillo M es un derecho R-módulo, luego el producto tensor con M rinde un functor F: R-Mod → Ab. El functor G: Ab → R-Mod, definida por G()A*Z()M,A) para cada grupo abeliano A, es un derecho a F.
- De monoides y grupos a anillos. La construcción integral de anillo monoide da un functor de monoides a anillos. Este functor se deja junto al functor que asocia a un anillo dado su monoide multiplicativo subyacente. Del mismo modo, la construcción de anillos de grupo integral produce un functor de grupos a anillos, a la izquierda junto al functor que asigna a un anillo dado su grupo de unidades. Uno también puede comenzar con un campo K y considerar la categoría de K- álgebras en lugar de la categoría de anillos, para conseguir el monoide y anillos de grupo sobre K.
- Campo de fracciones. Considerar la categoría Domm de dominios integrales con morfismos inyectables. El funerario olvidadizo Campo → Domm desde campos tiene una unión izquierda: asigna a cada dominio integral su campo de fracciones.
- Anillos polinomios. Vamos Anillo* ser la categoría de anillos comunicativos puntiagudos con unidad (pairs (A,a) donde A es un anillo, un mento A y morfismos conservan los elementos distinguidos). El funerario olvidadizo G:Anillo* → Anillo tiene una unión izquierda – asigna a cada anillo R el par (R[x],x) donde R[x] es el anillo polinomio con coeficientes de R.
- Abelianization. Considere el functor de inclusión G: Ab → Grp de la categoría de grupos abelianos a la categoría de grupos. Tiene una unión izquierda llamada abelianización que asigna a cada grupo G el grupo de referencia Gab=G/[G,G].
- El grupo Grothendieck. En K-teoría, el punto de partida es observar que la categoría de paquetes vectoriales en un espacio topológico tiene una estructura monoide conmutativa bajo suma directa. Uno puede hacer un grupo abeliano fuera de este monoide, el grupo Grothendieck, añadiendo formalmente un inverso aditivo para cada paquete (o clase de equivalencia). Alternativamente se puede observar que el functor que para cada grupo toma el monoide subyacente (ignorando inversos) tiene un conjunto izquierdo. Se trata de una construcción de una vez por todas, en consonancia con la tercera sección anterior. Es decir, uno puede imitar la construcción de números negativos; pero hay la otra opción de un teorema de existencia. Para el caso de estructuras algebraicas finitarias, la existencia por sí misma puede ser referida a álgebra universal, o teoría modelo; naturalmente también hay una prueba adaptada a la teoría de la categoría, también.
- Frobenius reciprocity en la teoría de la representación de grupos: ver representación inducida. Este ejemplo predijo la teoría general por medio siglo.
Topología
- Un funerario con una unión izquierda y derecha. Vamos G ser el functor de espacios topológicos a conjuntos que asocian a cada espacio topológico su conjunto subyacente (olvidando la topología, es decir). G tiene una unión izquierda F, crear el espacio discreto en un conjunto Y, y un derecho H crear la topología trivial en Y.
- Suspensiones y espacios de bucle. Ante espacios topológicos X y Y, el espacio [SX, Y] de clases de mapas de la suspensión SX de X a Y es naturalmente isomorfo al espacio [XΩY] de clases de mapas de homotopy X al espacio de bucle ΩY de Y. Por lo tanto, el functor de suspensión se deja junto al functor de espacio de bucle en la categoría homotopy, un hecho importante en la teoría de la homotopy.
- compactación Stone-Čech. Vamos KHaus ser la categoría de espacios compactos Hausdorff y G: KHaus → Top ser el functor de inclusión a la categoría de espacios topológicos. Entonces... G tiene una unión izquierda F: Top → KHaus, la compactación Stone-Čech. La unidad de este par adjoint produce un mapa continuo de cada espacio topológico X en su compactación Stone-Čech.
- Imágenes directas e inversas de cuchillas. Cada mapa continuo f: X → Y entre los espacios topológicos induce un functor f Alternativa de la categoría de cuchillas (de conjuntos, o grupos abelianos, o anillos...) en X a la categoría correspondiente Y, el directo functor de imagen. También induce a un functor f −1 de la categoría de olas de grupos abelianos Y de los grupos abelianos X, el inversor de imagen. f −1 está a la izquierda f Alternativa. Aquí un punto más sutil es que la unión izquierda para las cuchillas coherentes difiere de eso para las cuchillas (de conjuntos).
- Soberificación. El artículo sobre la dualidad de Piedra describe una adjunción entre la categoría de espacios topológicos y la categoría de espacios sobrios que se conoce como soberificación. Notablemente, el artículo también contiene una descripción detallada de otra orden que prepara el camino para la famosa dualidad de espacios sobrios y locales espaciales, explotados en topología inútil.
Poses
Todo conjunto parcialmente ordenado se puede ver como una categoría (donde los elementos del conjunto de poses se convierten en los objetos de la categoría y tenemos un solo morfismo de x a y si y solo si x ≤ y). Un par de funtores adjuntos entre dos conjuntos parcialmente ordenados se denomina conexión de Galois (o, si es contravariante, una conexión de Galois antítona). Consulte ese artículo para ver una serie de ejemplos: el caso de la teoría de Galois, por supuesto, es uno de los principales. Cualquier conexión de Galois da lugar a operadores de cierre ya biyecciones inversas que conservan el orden entre los elementos cerrados correspondientes.
Como es el caso de los grupos de Galois, el verdadero interés radica a menudo en refinar una correspondencia a una dualidad (es decir, isomorfismo de orden antítono). Un tratamiento de la teoría de Galois en este sentido por parte de Kaplansky influyó en el reconocimiento de la estructura general aquí.
El caso de orden parcial colapsa las definiciones adjuntas de manera bastante notable, pero puede proporcionar varios temas:
- las adjunciones pueden no ser dualidades o isomorfismos, pero son candidatos para actualizar a ese estado
- los operadores de cierre pueden indicar la presencia de adjunciones, como monadas correspondientes (cf. el cierre de Kuratowski axiomas)
- un comentario muy general de William Lawvere es que sintaxis y semántica are adjoint: take C ser el conjunto de todas las teorías lógicas (axiomatizaciones), y D el conjunto de poder del conjunto de todas las estructuras matemáticas. Para una teoría T dentro C, vamos G()T) ser el conjunto de todas las estructuras que satisfacen los axiomas T; para un conjunto de estructuras matemáticas S, vamos F()S) ser la axiomatización mínima de S. Podemos decir eso. S es un subconjunto de G()TSi y sólo si F()S) lógicamente implica T: el "semantics functor" G es un derecho al "divertidor sintético" F.
- división es (en general) el intento de invertidos multiplicación, pero en situaciones donde esto no es posible, a menudo intentamos construir un adjoint en su lugar: el cociente ideal se une a la multiplicación por los ideales del anillo, y la implicación en la lógica proposicional es unida a la conjunción lógica.
Teoría de categorías
- Equivalencias. Si F: D → C es una equivalencia de categorías, entonces tenemos una equivalencia inversa G: C → D, y los dos functores F y G formar un par de adjoint. La unidad y la counidad son isomorfismos naturales en este caso.
- Una serie de adjunciones. El functor π0 que asigna a una categoría su conjunto de componentes conectados es de conjunto izquierdo al functor D que asigna a un conjunto de la categoría discreta en ese conjunto. Además, D es zurdo-adjunto al functor objeto U que asigna a cada categoría su conjunto de objetos, y finalmente U es zurdo A que asigna a cada conjunto la categoría indiscreta en ese conjunto.
- Objeto exponencial. En una categoría cerrada cartesiana el endofunctor C → C dado por:A tiene una unión correcta –A. Este par se conoce a menudo como currying y uncurrying; en muchos casos especiales, también son continuos y forman un homeomorfismo.
Lógica categórica
- Cuantificación. Si φ φ Y{displaystyle phi _{Y}} es un predicado no irritante que expresa cierta propiedad, entonces una teoría de conjunto suficientemente fuerte puede probar la existencia del conjunto Y={}Sí.▪ ▪ φ φ Y()Sí.)}{displaystyle Y={ymid phi _{Y}(y)} de términos que cumplen la propiedad. Un subconjunto adecuado T⊂ ⊂ Y{displaystyle Tsubset Y} y la inyección asociada T{displaystyle T} en Y{displaystyle Sí. se caracteriza por un predicado φ φ T()Sí.)=φ φ Y()Sí.)∧ ∧ φ φ ()Sí.){displaystyle phi _{T}(y)=phi _{Y}(y)land varphi (y)} expresar una propiedad estrictamente más restrictiva.
- El papel de los cuantificadores en las lógicas predicadas es en la formación de propuestas y también en la expresión de complejos predicados mediante fórmulas de cierre con posiblemente más variables. Por ejemplo, considere un predicado ↑ ↑ f{displaystyle psi _{f} con dos variables abiertas X{displaystyle X} y Y{displaystyle Sí.. Usar un cuantificador para cerrar X{displaystyle X}, podemos formar el conjunto
- {}Sí.▪ ▪ Y▪ ▪ ∃ ∃ x.↑ ↑ f()x,Sí.)∧ ∧ φ φ S()x)}{displaystyle {yin Ymid exists x.,psi _{f}(x,y)land phi _{S}(x)}}
- de todos los elementos Sí.{displaystyle y} de Y{displaystyle Sí. para el cual hay x{displaystyle x} a la cual es ↑ ↑ f{displaystyle psi _{f}-relacionado, y que se caracteriza por la propiedad φ φ S{displaystyle phi _{S}. Establecer operaciones teóricas como la intersección ∩ ∩ {displaystyle cap } de dos conjuntos corresponde directamente a la conjunción ∧ ∧ {displaystyle land } de predicados. En lógica categórica, un subcampo de la teoría de topos, los cuantificadores se identifican con adjoints al functor de retroceso. Tal realización se puede ver en analogía con la discusión de la lógica proposicional utilizando la teoría de conjuntos, pero la definición general hace para una gama más rica de lógicas.
- Así que considere un objeto Y{displaystyle Sí. en una categoría con retrocesos. Cualquier morfismo f:X→ → Y{displaystyle f:Xto Sí. induce a un functor
- fAlternativa Alternativa :Subsidio()Y)restablecimiento restablecimiento Subsidio()X){displaystyle f^{*}:{text{Sub}}(Y)longrightarrow {text{Sub}(X)}
- en la categoría que es el preorden de subobjetos. Mapas subobjetos T{displaystyle T} de Y{displaystyle Sí. (técnicamente: clases de monomorfismo T→ → Y{displaystyle Tto Y}) a la retirada X× × YT{displaystyle Xtimes _{Y}T}. Si este functor tiene una unión izquierda o derecha, se llaman ∃ ∃ f{displaystyle exists _{f} y О О f{displaystyle forall _{f}, respectivamente. Ambos mapa desde Subsidio()X){displaystyle {text{Sub}(X)} volver a Subsidio()Y){displaystyle {text{Sub}(Y)}. Muy rudamente, dado un dominio S⊂ ⊂ X{displaystyle Ssubset X} para cuantificar una relación expresada f{displaystyle f} sobre, el functor/quantificador cierra X{displaystyle X} dentro X× × YT{displaystyle Xtimes _{Y}T} y devuelve el subconjunto especificado Y{displaystyle Sí..
- Ejemplo: En Set{displaystyle operatorname {Set}, la categoría de conjuntos y funciones, los subobjetos canónicos son el subconjunto (o más bien sus inyecciones canónicas). El retroceso fAlternativa Alternativa T=X× × YT{displaystyle f^{*}T=Xtimes ¿Qué? de una inyección de un subconjunto T{displaystyle T} en Y{displaystyle Sí. y f{displaystyle f} se caracteriza como el conjunto más grande que sabe todo f{displaystyle f} y la inyección de T{displaystyle T} en Y{displaystyle Sí.. Por lo tanto resulta ser (en bijección con) la imagen inversa f− − 1[T]⊆ ⊆ X{displaystyle f^{-1}[T]subseteq X..
- Para S⊆ ⊆ X{displaystyle Ssubseteq X}, vamos a averiguar el conjunto izquierdo, que se define a través de
- Hom()∃ ∃ fS,T).. Hom()S,fAlternativa Alternativa T),{displaystyle {operatorname {Hom}(exists _{f}S,T)cong {operatorname {Hom} (S,f^{*}T),}
- que aquí sólo significa
- ∃ ∃ fS⊆ ⊆ TAdministración Administración S⊆ ⊆ f− − 1[T]{displaystyle exists _{f} Ssubseteq Tleftrightarrow Ssubseteq f^{-1}[T].
- Considerar f[S]⊆ ⊆ T{displaystyle f[S]subseteq T}. Ya vemos. S⊆ ⊆ f− − 1[f[S]]⊆ ⊆ f− − 1[T]{displaystyle Ssubseteq f^{-1}[f[S]subseteq f^{-1}[T]. Por el contrario, Si para un x▪ ▪ S{displaystyle xin S} también tenemos x▪ ▪ f− − 1[T]{displaystyle xin f^{-1}[T], entonces claramente f()x)▪ ▪ T{displaystyle f(x)in T}. Así que... S⊆ ⊆ f− − 1[T]{displaystyle Ssubseteq f^{-1}[T] implicación f[S]⊆ ⊆ T{displaystyle f[S]subseteq T}. Concluimos que la izquierda se une al functor de imagen inversa fAlternativa Alternativa {displaystyle f^{*} es dada por la imagen directa. Aquí hay una caracterización de este resultado, que coincide más con la interpretación lógica: La imagen de S{displaystyle S. menores ∃ ∃ f{displaystyle exists _{f} es el conjunto completo de Sí.{displaystyle y}'s, tal que f− − 1[{}Sí.}]∩ ∩ S{displaystyle f^{-1} {fn}cap S} no es vacío. Esto funciona porque descuida exactamente aquellos Sí.▪ ▪ Y{displaystyle yin Y} que están en el complemento de f[S]{displaystyle f[S]. Así que...
- ∃ ∃ fS={}Sí.▪ ▪ Y▪ ▪ ∃ ∃ ()x▪ ▪ f− − 1[{}Sí.}]).x▪ ▪ S}=f[S].{displaystyle exists _{f}S={yin Ymid exists (xin f^{-1} [{y}]).,xin S;}=f[S].}
- Pon esto en analogía con nuestra motivación {}Sí.▪ ▪ Y▪ ▪ ∃ ∃ x.↑ ↑ f()x,Sí.)∧ ∧ φ φ S()x)}{displaystyle {yin Ymid exists x.,psi _{f}(x,y)land phi _{S}(x)}}.
- La unión derecha al functor de imagen inversa se da (sin hacer el cálculo aquí) por
- О О fS={}Sí.▪ ▪ Y▪ ▪ О О ()x▪ ▪ f− − 1[{}Sí.}]).x▪ ▪ S}.{displaystyle forall _{f}S={yin Ymidforall (xin f^{-1} [{y}]).,xin S;}
- El subconjunto О О fS{displaystyle forall _{f}S} de Y{displaystyle Sí. se caracteriza como el conjunto completo de Sí.{displaystyle y}'s con la propiedad que la imagen inversa de {}Sí.}{displaystyle {y}} con respecto a f{displaystyle f} está plenamente contenido S{displaystyle S.. Tenga en cuenta cómo el predicado que determina el conjunto es el mismo que antes, excepto que ∃ ∃ {displaystyle exists } es reemplazado por О О {displaystyle forall }.
- Vea también powerset.
Probabilidad
El hecho gemelo en probabilidad puede entenderse como un complemento: esa expectativa conmuta con transformada afín, y que la expectativa es, en cierto sentido, la mejor solución al problema de encontrar una aproximación de valor real a una distribución sobre los números reales.
Define una categoría basada en R{displaystyle mathbb {R}, con objetos siendo los números reales, y los morfismos siendo "funciones finas evaluadas en un punto". Es decir, para cualquier función affine f()x)=ax+b{displaystyle f(x)=ax+b} y cualquier número real r{displaystyle r}, definir un morfismo ()r,f):r→ → f()r){displaystyle (r,f):rto f(r)}.
Define una categoría basada en M()R){displaystyle M(mathbb {R})}, el conjunto de distribución de probabilidad en R{displaystyle mathbb {R} con una expectativa finita. Definir los morfismos en M()R){displaystyle M(mathbb {R})} como "funciones ajustadas evaluadas en una distribución". Es decir, para cualquier función affine f()x)=ax+b{displaystyle f(x)=ax+b} y cualquier μ μ ▪ ▪ M()R){displaystyle mu in M(mathbb {R})}, definir un morfismo ()μ μ ,f):r→ → μ μ ∘ ∘ f− − 1{displaystyle (muf):rto mu circ f^{-1}.
Luego, la medida Dirac delta define un functor: δ δ :x↦ ↦ δ δ x{displaystyle delta:xmapsto delta _{x}, y la expectativa define otro functor E:μ μ ↦ ↦ E[μ μ ]{displaystyle mathbb {E}:mu mapsto mathbb {E} [mu ]}, y están unidos: E⊣ ⊣ δ δ {displaystyle mathbb {E} dashv delta }. (Algo desconcertante, E{displaystyle mathbb {E} es la unión izquierda, aunque E{displaystyle mathbb {E} es "olvidado" y δ δ {displaystyle delta } es "libre".)
Adjuntos completos
Por lo tanto, existen numerosos funtores y transformaciones naturales asociados con cada adjunción, y solo una pequeña porción es suficiente para determinar el resto.
Un adjunto entre las categorías C y D consiste en
- Un functor F: D → C llamado izquierda
- Un functor G: C → D llamado derecho
- Un isomorfismo natural Ё: homC()F–,–) → homD(-G–)
- Una transformación natural ε: FG → 1C llamado counit
- Una transformación natural: 1D → GF llamado unidad
Una formulación equivalente, donde X denota cualquier objeto de C e Y denota cualquier objeto de D, es como sigue:
- Por todos C- morfismo f: FY → X, hay un único D- morfismo ⋅Y, X()f) g: Y → GX de tal manera que los diagramas de abajo conmutan, y por cada D- morfismo g: Y → GX, hay un único C- morfismo ⋅−1Y, X()g) f: FY → X dentro C tal que los diagramas de abajo conmutan:
De esta afirmación, se puede recuperar que:
- Las transformaciones ε, pira y Ё están relacionadas por las ecuaciones
- f=CCPR CCPR Y,X− − 1()g)=ε ε X∘ ∘ F()g)▪ ▪ homC()F()Y),X)g=CCPR CCPR Y,X()f)=G()f)∘ ∘ .. Y▪ ▪ homD()Y,G()X))CCPR CCPR GX,X− − 1()1GX)=ε ε X▪ ▪ homC()FG()X),X)CCPR CCPR Y,FY()1FY)=.. Y▪ ▪ homD()Y,GF()Y)){displaystyle {begin{aligned}f= Phi _{Y,X}{-1}(g) ¿Por qué? _{Y,X}(f)circ eta ¿Por qué? ¿Qué? _{C}(FG(X),X)\\ Phi _{Y,FY}(1_{FY}) - ¿Qué?
- Las transformaciones ε, pira satisfacen las ecuaciones counit-unit
- 1FY=ε ε FY∘ ∘ F().. Y)1GX=G()ε ε X)∘ ∘ .. GX{displaystyle {begin{aligned}1_{FY} ################################################################################################################################################################################################################################################################ ¿Por qué? ¿Por qué? ¿Qué?
- Cada par (GX, εX) es un morfismo terminal de F a X dentro C
- Cada par (FY, piraY) es un morfismo inicial de Y a G dentro D
En particular, las ecuaciones anteriores permiten definir Φ, ε y η en términos de cualquiera de los tres. Sin embargo, los funtores adjuntos F y G por sí solos en general no son suficientes para determinar la adjunción. La equivalencia de estas situaciones se demuestra a continuación.
Los morfismos universales inducen la adjunción hom-set
Dado un funtor adjunto derecho G: C → D; en el sentido de los morfismos iniciales, uno puede construir la adjunción hom-set inducida siguiendo los siguientes pasos.
- Construir un functor F: D → C y una vía de transformación natural.
- Para cada objeto Y dentro D, elegir un morfismo inicial (F()Y.Y) de Y a G, así que esa piraY: Y → G()F()Y)). Tenemos el mapa de F sobre objetos y la familia de los morfismos.
- Para cada uno f: Y0 → Y1, como (F()Y0.Y0) es un morfismo inicial, luego factorizar piraY1 o f con la AutoridadY0 y conseguir F()f) F()Y0) → F()Y1). Este es el mapa F sobre morfismos.
- El diagrama de conmutación de esa factorización implica el diagrama de conmutación de las transformaciones naturales, por lo que pira: 1D → G o F es una transformación natural.
- Uniqueness of that factorization and that G es un functor implica que el mapa F sobre morfismos conserva composiciones e identidades.
- Construir un isomorfismo natural Ё: homC()F-,- → homD(-G-).
- Para cada objeto X dentro C, cada objeto Y dentro D, como (F()Y.Y) es un morfismo inicial, luego ЁY, X es una bijección, donde ЁY, X()f: F()Y) → X) G()f) o.Y.
- Es una transformación natural, G es un functor, entonces para cualquier objeto X0, X1 dentro C, cualquier objeto Y0, Y1 dentro D, cualquier x: X0 → X1, cualquier Sí.: Y1 → Y0, tenemos VIEWY1, X1()x o f o F()Sí.) = G(x) o G()f) o G()F()Sí.) o.Y1 = G()x) o G()f) o.Y0 o Sí. = G()x) o CCPRY0, X0()f) o Sí., y luego Ё es natural en ambos argumentos.
Un argumento similar permite construir una adjunción hom-set a partir de los morfismos terminales a un funtor adjunto izquierdo. (La construcción que comienza con un adjunto derecho es un poco más común, ya que el adjunto derecho en muchos pares de adjuntos es una inclusión definida trivialmente o un funtor olvidadizo).
La adjunción país-unidad induce la adjunción hom-set
Dados functores F: D → C, G: C → D, y un counit-unit adjunction (ε, pira): F ⊣ ⊣ {displaystyle dashv } G, podemos construir una adjunción hom-set encontrando la transformación natural ⋅: homC()F-,- → homD(-G-) en los siguientes pasos:
- Para cada uno f: FY → X y cada uno g: Y → GX, definir
- CCPR CCPR Y,X()f)=G()f)∘ ∘ .. YΨ Ψ Y,X()g)=ε ε X∘ ∘ F()g){displaystyle {begin{aligned}Phi _{Y,X}(f)=G(f)circ eta ¿Por qué? _{Y,X}(g)=varepsilon ¿Qué?
- Las transformaciones Ё y Ψ son naturales porque pira y ε son naturales.
- Usando, en orden, eso F es un functor, que ε es natural, y la ecuación de unidad de counidad 1FY = εFY o F(CAP)Y), obtenemos
- Ψ Ψ CCPR CCPR f=ε ε X∘ ∘ FG()f)∘ ∘ F().. Y)=f∘ ∘ ε ε FY∘ ∘ F().. Y)=f∘ ∘ 1FY=f{displaystyle {begin{aligned} Psi Phi fular=varepsilon FG(f)circ F(eta) ¿Por qué? ################################################################################################################################################################################################################################################################ ¿Por qué? 1_{FY}=fend{aligned}
- por lo tanto Ψ La reestructuración es la transformación de la identidad.
- Dualmente, usando eso G es un functor, que la pira es natural, y la ecuación de unidad de la counidad 1GX = G(ε)X) o.GX, obtenemos
- CCPR CCPR Ψ Ψ g=G()ε ε X)∘ ∘ GF()g)∘ ∘ .. Y=G()ε ε X)∘ ∘ .. GX∘ ∘ g=1GX∘ ∘ g=g{displaystyle {begin{aligned} Phi Psi gi=G(varepsilon GF(g)circo eta ¿Por qué? ¿Por qué? ################################################################################################################################################################################################################################################################ g\=1_{GX}circ G=gend{aligned}
- por lo tanto ЁΦ es la transformación de la identidad. Así Ё es un isomorfismo natural con Ё inverso−1 = Ψ.
La adjunción Hom-set induce todo lo anterior
Funtores dados F: D → C, G: C → D, y un complemento hom-set Φ: homC(F-,-) → homD(-,G-), uno puede construir una adjunción de unidad-país
- ()ε ε ,.. ):F⊣ ⊣ G{displaystyle (varepsiloneta): Fdashv G},
que define familias de morfismos iniciales y terminales, en los siguientes pasos:
- Vamosε ε X=CCPR CCPR GX,X− − 1()1GX)▪ ▪ homC()FGX,X){displaystyle varepsilon _{X}=Phi _{GX,X}{-1}(1_{GX})in mathrm {hom} ¿Qué?para cada uno X dentro C, donde1GX▪ ▪ homD()GX,GX){displaystyle 1_{GX}in mathrm {hom} _{D}(GX,GX)}es el morfismo de identidad.
- Vamos.. Y=CCPR CCPR Y,FY()1FY)▪ ▪ homD()Y,GFY){displaystyle eta _{Y}=Phi _{Y,FY}(1_{FY})in mathrm {hom} - Sí.para cada uno Y dentro D, donde1FY▪ ▪ homC()FY,FY){displaystyle 1_{FY}in mathrm {hom} ¿Por qué?es el morfismo de identidad.
- La bijetividad y la naturalidad de Ё implican que cada uno (GX, εX) es un morfismo terminal de F a X dentro C, y cada uno (FY, piraY) es un morfismo inicial de Y a G dentro D.
- La naturalidad de Ё implica la naturalidad del ε y de la piraa, y las dos fórmulas
- CCPR CCPR Y,X()f)=G()f)∘ ∘ .. YCCPR CCPR Y,X− − 1()g)=ε ε X∘ ∘ F()g){displaystyle {begin{aligned}Phi _{Y,X}(f)=G(f)circ eta ¿Por qué? ¿Qué?
- para cada uno f: FY → X y g: Y → GX (que determina completamente ⋅).
- Sustitución FY para X and piraY CCPRY, FY(1FYPara g en la segunda fórmula da la primera ecuación de unidad
- 1FY=ε ε FY∘ ∘ F().. Y){displaystyle 1_{FY}=varepsilon ################################################################################################################################################################################################################################################################ - Sí.,
- y sustitución GX para Y and εX CCPR−1GX, X(1GXPara f en la primera fórmula da la segunda ecuación de unidad
- 1GX=G()ε ε X)∘ ∘ .. GX{displaystyle 1_{GX}=G(varepsilon ¿Por qué?.
Propiedades
Existencia
No todos los funtores G: C → D admite un adjunto izquierdo. Si C es una categoría completa, entonces los funtores con adjuntos a la izquierda se pueden caracterizar por el teorema del funtor adjunto de Peter J. Freyd: G tiene un adjunto izquierdo si y solo si es continuo y se satisface cierta condición de pequeñez: para cada objeto Y de D existe una familia de morfismos
- fi: Y → G()Xi)
donde los índices i provienen de un conjunto I, no es una clase adecuada, tal que cada morfismo
- h: Y → G()X)
se puede escribir como
- h = G()t∘ fi
para alguna i en I y algo de morfismo
- t: Xi → X ▪ C.
Una declaración análoga caracteriza a los funtores con un adjunto derecho.
Un caso especial importante es el de las categorías localmente presentables. Si F:C→ → D{displaystyle F:Cto D} es un functor entre categorías localmente presentables, entonces
- F tiene una unión derecha si y sólo si F conserva pequeños límites
- F tiene una unión izquierda si y sólo si F preserva pequeños límites y es un functor accesible
Singularidad
Si el funtor F: D → C tiene dos adjuntos derechos G y G′, entonces G y G′ son naturalmente isomorfos. Lo mismo es cierto para los adjuntos izquierdos.
Por el contrario, si F se deja adjunto a G, y G es naturalmente isomorfo a G′ entonces F también se deja adjunto a G′. De manera más general, si 〈F, G, ε, η〉 es un complemento (con unidad-país (ε,η)) y
- σ: F → F.
- τ: G → G.
son isomorfismos naturales, entonces 〈F′, G′, ε′, η′〉 es un complemento donde
- .. .=()τ τ Alternativa Alternativa σ σ )∘ ∘ .. ε ε .=ε ε ∘ ∘ ()σ σ − − 1Alternativa Alternativa τ τ − − 1).{displaystyle {begin{aligned}eta ' sensible=(tau ast sigma)circ eta \\varepsilon 'щ=varepsilon circ (sigma ^{-1}ast tau ^{-1}). {fnK}}
Aquí. ∘ ∘ {displaystyle circ } denota la composición vertical de las transformaciones naturales, y Alternativa Alternativa {displaystyle ast } denota composición horizontal.
Composición
Los adjuntos se pueden componer de forma natural. Específicamente, si 〈F, G, ε, η〉 es un complemento entre C y D y 〈F′, G′, ε′, η′〉 es un complemento entre D y E entonces el funtor
- F∘ ∘ F.:E→ → C{displaystyle Fcirc F'Erightarrow C}
se deja junto a
- G.∘ ∘ G:C→ → E.{displaystyle G'circ G:Cto E.}
Más precisamente, hay un adjunto entre F F' y G' G con unidad y counit dadas respectivamente por las composiciones:
- 1E→.. .G.F.→G... F.G.GFF.FF.G.G→Fε ε .GFG→ε ε 1C.{displaystyle {begin{aligned} {E}{xrightarrow {eta}G'F'{xrightarrow {G'eta F'}G'GFF'\\\cHFF'G{xrightarrow {Fvarepsilon 'G}FG{xrightarrow {varepsilon {fnMicrosoft Sans Serif}
Este nuevo adjunto se llama la composición de los dos adjuntos dados.
Puesto que también hay una forma natural de definir una adjunción de identidad entre una categoría C y ella misma, se puede formar una categoría cuyos objetos sean todas categorías pequeñas y cuyos morfismos sean adjunciones.
Limitar la conservación
La propiedad más importante de los adjuntos es su continuidad: cada funtor que tiene un adjunto izquierdo (y por lo tanto es un adjunto derecho) es continuo (es decir, conmuta con límites en la categoría sentido teórico); cada funtor que tiene un adjunto derecho (y por lo tanto es un adjunto izquierdo) es cocontinuo (es decir, conmuta con colimits).
Dado que muchas construcciones comunes en matemáticas son límites o colímites, esto proporciona una gran cantidad de información. Por ejemplo:
- aplicar un functor adjunto derecho a un producto de objetos produce el producto de las imágenes;
- aplicar un functor adjoint izquierdo a un coproducto de objetos produce el coproducto de las imágenes;
- todo functor adjunto derecho entre dos categorías abelianas queda exacto;
- cada functor adjunto izquierdo entre dos categorías abelianas es exacto derecho.
Aditividad
Si C y D son categorías preaditivas y F: D → C es un funtor aditivo con un adjunto derecho G: C → D, entonces G también es un funtor aditivo y las biyecciones hom-set
- CCPR CCPR Y,X:homC()FY,X).. homD()Y,GX){displaystyle Phi ¿Qué?
son, de hecho, isomorfismos de grupos abelianos. Dualmente, si G es aditivo con un adjunto izquierdo F, entonces F también es aditivo.
Además, si tanto C como D son categorías aditivas (es decir, categorías preaditivas con todos los subproductos finitos), entonces cualquier par de funtores adjuntos entre ellos es automáticamente aditivo.
Relaciones
Construcciones universales
Como se indicó anteriormente, una adjunción entre las categorías C y D da lugar a una familia de morfismos universales, uno para cada objeto en C y uno para cada objeto en D. Por el contrario, si existe un morfismo universal para un funtor G: C → D de cada objeto de D, entonces G tiene un adjunto izquierdo.
Sin embargo, las construcciones universales son más generales que los funtores adjuntos: una construcción universal es como un problema de optimización; da lugar a un par adjunto si y solo si este problema tiene una solución para cada objeto de D (equivalentemente, cada objeto de C).
Equivalencias de categorías
Si un funtor F: D → C es la mitad de una equivalencia de categorías, entonces es el adjunto izquierdo en una equivalencia adjunta de categorías, es decir, una adjunción cuya unidad y counidad son isomorfismos.
Cada adjunto 〈F, G, ε, η〉 extiende una equivalencia de ciertas subcategorías. Defina C1 como la subcategoría completa de C que consta de los objetos X de C para el cual εX es un isomorfismo, y define D1 como la subcategoría completa de D que consta de aquellos objetos Y de D para los cuales ηY es un isomorfismo. Entonces F y G pueden restringirse a D1 y C 1 y producir equivalencias inversas de estas subcategorías.
En cierto sentido, entonces, los adjuntos son "generalizados" inversos Tenga en cuenta, sin embargo, que un inverso derecho de F (es decir, un funtor G tal que FG es naturalmente isomorfo a 1D) no necesita ser un adjunto derecho (o izquierdo) de F. Los adjuntos generalizan los inversos de dos lados.
Mónadas
Cada adjunción 〈F, G, ε, η〉 da lugar a una mónada asociada 〈T, η, μ〉 en el categoría D. el funtor
- T:D→ → D{displaystyle T:{mathcal {}to {fnMithcal}}
está dado por T = GF. La unidad de la mónada
- .. :1D→ → T{displaystyle eta:1_{mathcal {D}to T}
es solo la unidad η de la adjunción y la transformación de multiplicación
- μ μ :T2→ → T{displaystyle mu:T^{2}to T,}
está dado por μ = GεF. Dualmente, el triple 〈FG, ε, FηG〉 define una comonad en C.
Cada mónada surge de alguna adjunción (de hecho, típicamente de muchas adjunciones) de la manera anterior. Dos construcciones, llamadas la categoría de álgebras de Eilenberg-Moore y la categoría de Kleisli, son dos soluciones extremas al problema de construir una adjunción que dé lugar a una mónada dada.
Contenido relacionado
Teoría del valor extremo
Jacob Bernoulli
Categoría (matemáticas)
































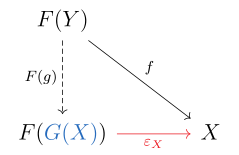


























































![f^{{-1}}[T]subseteq X](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a55cb02881c04c713a24cbe82ece550243ab558)


![exists _{f}Ssubseteq Tleftrightarrow Ssubseteq f^{-1}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c821337e6e35974fb9c9d1977c1a3b5da169aab)
![f[S]subseteq T](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b5dbaa58a61b4955053e8d30ee59bfe257e6c4c)
![Ssubseteq f^{{-1}}[f[S]]subseteq f^{{-1}}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c2845f7f5ca6c49df476c5de6e8c4c4385f1539)

![xin f^{{-1}}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/43e43732bf6ed7b2b03201f6bbb1eea85f573f74)

![Ssubseteq f^{-1}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad773de89f2d30a93a8442ac7c86eb44e8980bd)


![f^{-1}[{y}]cap S](https://wikimedia.org/api/rest_v1/media/math/render/svg/872d2d997b54463e913e7ea72920cfe094e89342)

![f[S]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc136e58f23572a4001b784eea645e59b735ce49)
![exists _{f}S={yin Ymid exists (xin f^{-1}[{y}]).,xin S;}=f[S].](https://wikimedia.org/api/rest_v1/media/math/render/svg/24265e6a1e4e9b58e13a76ba7662185d2527e460)
![forall _{f}S={yin Ymid forall (xin f^{-1}[{y}]).,xin S;}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/a92d205846301c35cf45cd5cf9e17c4fd5937bd3)












![{displaystyle mathbb {E}:mu mapsto mathbb {E} [mu ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dbb67a1098a8750cec80a69e8213449b0505576)


























