Funciones trigonométricas inversas

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Funciones inversas de las funciones trigonométricas

En matemáticas, las funciones trigonométricas inversas (ocasionalmente también llamadas funciones de arco, funciones antitrigonométricas o funciones ciclométricas) son las funciones inversas de las funciones trigonométricas (con dominios adecuadamente restringidos). Específicamente, son las inversas de las funciones seno, coseno, tangente, cotangente, secante y cosecante, y se utilizan para obtener un ángulo a partir de cualquiera de las razones trigonométricas del ángulo. Las funciones trigonométricas inversas se utilizan ampliamente en ingeniería, navegación, física y geometría.

Notación

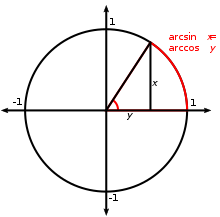
Existen varias notaciones para las funciones trigonométricas inversas. La convención más común es nombrar funciones trigonométricas inversas usando un prefijo de arco: $arcsin(x)$ , $arccos(x)$ , $arctan(x)$ , etc. (Esta convención se utiliza en todo este artículo). Esta notación surge de las siguientes relaciones geométricas: al medir en radianes, un ángulo de $θ$ radianes corresponderá a un arco cuya longitud es $rθ$ , donde $r$ es el radio del círculo. Así, en el círculo unitario, "el arco cuyo coseno es $x$ " es igual que "el ángulo cuyo coseno es $x$ ", porque la longitud del arco del un círculo en radios es lo mismo que la medida del ángulo en radianes. En los lenguajes de programación de computadoras, las funciones trigonométricas inversas a menudo se denominan con las formas abreviadas asin, acos, atan.

Las notaciones $pecado -1 () x)$ , $# -1 () x)$ , $# -1 () x)$ , etc., como lo introdujo John Herschel en 1813, se utilizan a menudo también en fuentes de lengua inglesa, mucho más que el establecido también $pecado [1 - 1] () x)$ , $# [1 - 1] () x)$ , $# [1 - 1] () x)$ – convenciones consistentes con la notación de una función inversa, que es útil (por ejemplo) para definir la versión multivalorada de cada función trigonométrica inversa: ${displaystyle tan ^{-1}(x)={arctan(x)+pi kmid kin mathbb {Z} }~.}$ Sin embargo, esto podría parecer un conflicto lógicamente con la semántica común para expresiones tales como $pecado 2 () x)$ (aunque sólo $pecado 2 x$ , sin paréntesis, es el uso muy común), que se refiere a la potencia numérica en lugar de la composición de la función, y por lo tanto puede resultar en confusión entre notación para la función recíproca (multiplicativa inversa) e inversa.

La confusión se ve mitigada en cierta medida por el hecho de que cada una de las funciones trigonométricas recíprocas tiene su propio nombre, por ejemplo, $(cos(x)) -1 = seg(x)$ . Sin embargo, algunos autores desaconsejan su uso por ser ambiguo. Otra convención precaria utilizada por un pequeño número de autores es utilizar una primera letra mayúscula, junto con un superíndice “ $-1$ ”: $Sin -1 (x)$ , $Cos -1 (x)$ , $Tan -1 (x)$ , etc. Aunque se pretende evitar confusiones con el recíproco, que debe estar representado por $sin -1 (x)$ , $cos -1 (x)$ , etc., o, mejor, por $sin -1 x$ , $cos -1 x$ , etc., a su vez crea todavía Otra fuente importante de ambigüedad, especialmente porque muchos lenguajes de programación populares de alto nivel (por ejemplo, Mathematica y MAGMA) usan esas mismas representaciones en mayúscula para las funciones trigonométricas estándar, mientras que otros (Python, SymPy, NumPy, Matlab, MAPLE, etc.) utilizar minúsculas.

Por lo tanto, desde 2009, la norma ISO 80000-2 ha especificado únicamente el "arco" prefijo para las funciones inversas.

Conceptos básicos

Valores principales

Dado que ninguna de las seis funciones trigonométricas es uno a uno, deben restringirse para tener funciones inversas. Por lo tanto, los rangos de resultados de las funciones inversas son subconjuntos propios (es decir, estrictos) de los dominios de las funciones originales.

Por ejemplo, usando función en el sentido de funciones multivaloradas, así como la función de raíz cuadrada $y={sqrt {x}}$ podría definirse ${displaystyle y^{2}=x,}$ la función ${displaystyle y=arcsin(x)}$ se define de modo que ${displaystyle sin(y)=x.}$ Para un número real dado $x,$ con ${displaystyle -1leq xleq 1,}$ hay múltiples (de hecho, contablemente muchos) números $y$ tales que ${displaystyle sin(y)=x}$ ; por ejemplo, ${displaystyle sin(0)=0,}$ pero también ${displaystyle sin(pi)=0,}$ ${displaystyle sin(2pi)=0,}$ etc. Cuando sólo se desea un valor, la función puede ser restringida a su rama principal. Con esta restricción, para cada uno $x$ en el dominio, la expresión $arcsin(x)$ evaluará sólo a un valor único, llamado su valor principal. Estas propiedades se aplican a todas las funciones trigonométricas inversas.

Las principales inversas se enumeran en la siguiente tabla.

Nombre	Notación habitual	Definición	Dominio de $x$ para el resultado real	Rango de valor principal habitual (radianos)	Rango de valor principal habitual (de acuerdo)
arcsine	${displaystyle y=arcsin(x)}$	$x = pecado(Sí.)$	${displaystyle -1leq xleq 1}$	${displaystyle -{frac {pi }{2}}leq yleq {frac {pi }{2}}}$	${displaystyle -90^{circ }leq yleq 90^{circ }}$
arccosine	${displaystyle y=arccos(x)}$	$x = cos(Sí.)$	${displaystyle -1leq xleq 1}$	${displaystyle 0leq yleq pi }$	${displaystyle 0^{circ }leq yleq 180^{circ }}$
arctangent	${displaystyle y=arctan(x)}$	$x = bronceado Sí.)$	todos los números reales	$<math alttext="{displaystyle -{frac {pi }{2}}<y− − π π 2.Sí..π π 2{displaystyle - ¿Qué? ♪♪♪♪♪♪ } {2}}<img alt="{displaystyle -{frac {pi }{2}}<y$	$<math alttext="{displaystyle -90^{circ }<y− − 90∘ ∘ .Sí..90∘ ∘ {displaystyle -90^{circ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪♪<img alt="{displaystyle -90^{circ }<y$
arccotangent	${displaystyle y=operatorname {arccot}(x)}$	$x = cot(Sí.)$	todos los números reales	$<math alttext="{displaystyle 0<y0.Sí..π π {displaystyle 0traducido <img alt="{displaystyle 0<y$	$<math alttext="{displaystyle 0^{circ }<y0∘ ∘ .Sí..180∘ ∘ {displaystyle 0^{circ }traducido<img alt="{displaystyle 0^{circ }<y$
arcsecant	${displaystyle y=operatorname {arcsec}(x)}$	$x = sec(Sí.)$	${displaystyle {leftvert xrightvert }geq 1}$	$<math alttext="{displaystyle 0leq y<{frac {pi }{2}}{text{ or }}{frac {pi }{2}}0≤ ≤ Sí..π π 2oπ π 2.Sí.≤ ≤ π π {displaystyle 0leq y won}{f} {f} {f}{f} {f} {f}} {f}}} {f}} {f}}} {f}}}f}} {f}}}} {f}f} - ¿Qué?<img alt="{displaystyle 0leq y<{frac {pi }{2}}{text{ or }}{frac {pi }{2}}$	$<math alttext="{displaystyle 0^{circ }leq y<90^{circ }{text{ or }}90^{circ }0∘ ∘ ≤ ≤ Sí..90∘ ∘ o90∘ ∘ .Sí.≤ ≤ 180∘ ∘ {displaystyle 0^{circ }leq y se hicieron realidad {circ }{text{ or }90^{circ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪♪<img alt="{displaystyle 0^{circ }leq y<90^{circ }{text{ or }}90^{circ }$
arccosecant	${displaystyle y=operatorname {arccsc}(x)}$	$x = csc(Sí.)$	${displaystyle {leftvert xrightvert }geq 1}$	$<math alttext="{displaystyle -{frac {pi }{2}}leq y<0{text{ or }}0− − π π 2≤ ≤ Sí..0o0.Sí.≤ ≤ π π 2{displaystyle -{frac {pi}{2}leq y made0{text{ or }0cantado ♪ } {2}}<img alt="{displaystyle -{frac {pi }{2}}leq y<0{text{ or }}0$	$<math alttext="{displaystyle -90^{circ }leq y<0^{circ }{text{ or }}0^{circ }− − 90∘ ∘ ≤ ≤ Sí..0∘ ∘ o0∘ ∘ .Sí.≤ ≤ 90∘ ∘ {displaystyle -90^{circ }leq y se hicieron {circ }{text{ or }0^{circ} - ¿Qué?<img alt="{displaystyle -90^{circ }leq y<0^{circ }{text{ or }}0^{circ }$

Nota: Algunos autores definen el rango de arcsecant para ser $<math alttext="{textstyle (0leq y<{frac {pi }{2}}{text{ or }}pi leq y()0≤ ≤ Sí..π π 2oπ π ≤ ≤ Sí..3π π 2){textstyle (0leq y made{frac {pi}{2}{text{ or }pi leq yse{frac {3pi}}} {f}f}}pppppppppccccccH3cccH3f}}f}f}fnf}f}f}ppppppf}ppppppppppccpccccccccccccccpcccccccccccccccH3cH3cH3cH3cH3cH3ccH3cH3cH3c } {2}}}<img alt="{textstyle (0leq y<{frac {pi }{2}}{text{ or }}pi leq y$ , porque la función tangente no es negativa en este dominio. Esto hace que algunos cálculos sean más consistentes. Por ejemplo, usando este rango, ${displaystyle tan(operatorname {arcsec}(x))={sqrt {x^{2}-1}},}$ mientras que con el rango $<math alttext="{textstyle (0leq y<{frac {pi }{2}}{text{ or }}{frac {pi }{2}}()0≤ ≤ Sí..π π 2oπ π 2.Sí.≤ ≤ π π ){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {pi}{2}} {fnMicroc {f} {fnMicroc}}} {fnMicroc}}} {fnMicroc}} {fnMicroc}}}} {f}} {f}}}} {f}}}}}}}}}} {f}}}}}}}}}} {f}}} {f}}}}} {f} {f}} {f}f}f}f}f}}}f}f} {f}f} {f}f}f}}}}}}f}}} {b}f}f}f} {f}f}fnMinMinMinMinMinMinMinKf}}}}}}}}}}fnMi<img alt="{textstyle (0leq y<{frac {pi }{2}}{text{ or }}{frac {pi }{2}}$ , tendríamos que escribir ${displaystyle tan(operatorname {arcsec}(x))=pm {sqrt {x^{2}-1}},}$ ya que el tangente no es negativo $<math alttext="{textstyle 0leq y0≤ ≤ Sí..π π 2,{textstyle 0leq y won {frac}{2}}<img alt="{textstyle 0leq y$ pero no positivo $<math alttext="{textstyle {frac {pi }{2}}π π 2.Sí.≤ ≤ π π .{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {f}fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {f}f}fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fn - ¿Qué?<img alt="{textstyle {frac {pi }{2}}$ Por una razón similar, los mismos autores definen el rango de arccosecant para ser $<math alttext="{textstyle (-pi ()- - π π .Sí.\leq \leq - - π π 2{fnMicrosoft Sans Serif} } {2}} <img alt="{textstyle (-pi$ o $<math alttext="{textstyle 00.Sí.\leq \leq π π 2).{textstyle 0 madeyleq {pi}}} <img alt="{textstyle 0$

Si $x$ se permite ser un número complejo, luego el rango de $y$ aplica sólo a su parte real.

La siguiente tabla muestra los nombres y dominios de las funciones trigonométricas inversas junto con el rango de sus valores principales habituales en radianes.

Nombre	Signatura		Dominio		Imagen/Range	Inverso función		Dominio		Imagen de valores principales
sine	$sin$	$:$	$mathbb {R}$	$to$	$[-1, 1]$	${displaystyle arcsin }$	$:$	$[-1, 1]$	$to$	${displaystyle left[-{tfrac {pi }{2}},{tfrac {pi }{2}}right]}$
Cosine	$cos$	$:$	$mathbb {R}$	$to$	$[-1, 1]$	$arccos$	$:$	$[-1, 1]$	$to$	$[0,pi ]$
tangente	$tan$	$:$	${displaystyle pi mathbb {Z} +left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)}$	$to$	$mathbb {R}$	$arctan$	$:$	$mathbb {R}$	$to$	${displaystyle left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)}$
cotangent	$cot$	$:$	${displaystyle pi mathbb {Z} +(0,pi)}$	$to$	$mathbb {R}$	$operatorname{arccot}$	$:$	$mathbb {R}$	$to$	${displaystyle (0,pi)}$
secant	$sec$	$:$	${displaystyle pi mathbb {Z} +left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)}$	$to$	${displaystyle mathbb {R} setminus (-1,1)}$	${displaystyle operatorname {arcsec} }$	$:$	${displaystyle mathbb {R} setminus (-1,1)}$	$to$	${displaystyle [,0,;pi ,];;;setminus left{{tfrac {pi }{2}}right}}$
cosecante	$csc$	$:$	${displaystyle pi mathbb {Z} +(0,pi)}$	$to$	${displaystyle mathbb {R} setminus (-1,1)}$	${displaystyle operatorname {arccsc} }$	$:$	${displaystyle mathbb {R} setminus (-1,1)}$	$to$	${displaystyle left[-{tfrac {pi }{2}},{tfrac {pi }{2}}right]setminus {0}}$

El símbolo ${displaystyle mathbb {R} =(-inftyinfty)}$ denota el conjunto de todos los números reales y ${displaystyle mathbb {Z} ={ldots,-2,,-1,,0,,1,,2,,ldots }}$ denota el conjunto de todos los enteros. El conjunto de todos los números enteros de $pi$ es denotado por

{displaystyle pi mathbb {Z} ~:=~{pi n;:;nin mathbb {Z} }~=~{ldots,-2pi,-pi,0,,pi,2pi,ldots }.}

El símbolo ${displaystyle ,setminus ,}$ denotes set subtraction so that, for instance, ${displaystyle mathbb {R} setminus (-1,1)=(-infty-1]cup [1,infty)}$ es el conjunto de puntos en $mathbb {R}$ (es decir, números reales) que son no en el intervalo ${displaystyle (-1,1).}$

La nota de la suma de Minkowski ${textstyle pi mathbb {Z} +(0,pi)}$ y ${displaystyle pi mathbb {Z} +{bigl (}{-{tfrac {pi }{2}}},{tfrac {pi }{2}}{bigr)}}$ que se utiliza arriba para escribir concisamente los dominios de ${displaystyle cotcsctan{text{ and }}sec }$ se explica ahora.

Domain of cotangent $cot$ and cosecant $csc$ : Los dominios de ${displaystyle ,cot ,}$ y ${displaystyle ,csc ,}$ son iguales. Son el conjunto de todos los ángulos $theta$ en que ${displaystyle sin theta neq 0,}$ i.e. todos los números reales que son no de la forma ${displaystyle pi n}$ para algunos enteros ${displaystyle n,}$

{displaystyle {begin{aligned}pi mathbb {Z} +(0,pi)&=cdots cup (-2pi-pi)cup (-pi0)cup (0,pi)cup (pi2pi)cup cdots \&=mathbb {R} setminus pi mathbb {Z} end{aligned}}}

Dominio de tangente $tan$ y secant $sec$ : Los dominios de ${displaystyle ,tan ,}$ y ${displaystyle ,sec ,}$ son iguales. Son el conjunto de todos los ángulos $theta$ en que ${displaystyle cos theta neq 0,}$

{displaystyle {begin{aligned}pi mathbb {Z} +left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)&=cdots cup {bigl (}{-{tfrac {3pi }{2}}},{-{tfrac {pi }{2}}}{bigr)}cup {bigl (}{-{tfrac {pi }{2}}},{tfrac {pi }{2}}{bigr)}cup {bigl (}{tfrac {pi }{2}},{tfrac {3pi }{2}}{bigr)}cup cdots \&=mathbb {R} setminus left({tfrac {pi }{2}}+pi mathbb {Z} right)\end{aligned}}}

Soluciones a ecuaciones trigonométricas elementales

Cada una de las funciones trigonométricas es periódica en la parte real de su argumento, corriendo a través de todos sus valores dos veces en cada intervalo de ${displaystyle 2pi:}$

Sine y cosecante comienzan su período en ${textstyle 2pi k-{frac {pi }{2}}}$ (donde) $k$ es un entero), terminarlo en ${textstyle 2pi k+{frac {pi }{2}},}$ y luego se revierten ${textstyle 2pi k+{frac {pi }{2}}}$ a ${textstyle 2pi k+{frac {3pi }{2}}.}$
Cosine y secant comienzan su periodo en ${displaystyle 2pi k,}$ terminarlo en ${displaystyle 2pi k+pi.}$ y luego se revierten ${displaystyle 2pi k+pi }$ a ${displaystyle 2pi k+2pi.}$
Tangent comienza su periodo en ${textstyle 2pi k-{frac {pi }{2}},}$ termina en ${textstyle 2pi k+{frac {pi }{2}},}$ y luego lo repite (para adelante) ${textstyle 2pi k+{frac {pi }{2}}}$ a ${textstyle 2pi k+{frac {3pi }{2}}.}$
El agente comienza su período ${displaystyle 2pi k,}$ termina en ${displaystyle 2pi k+pi}$ y luego lo repite (para adelante) ${displaystyle 2pi k+pi }$ a ${displaystyle 2pi k+2pi.}$

Esta periodicidad se refleja en los inversos generales, donde $k$ es un entero.

La tabla siguiente muestra cómo se pueden utilizar funciones trigonométricas inversas para resolver las igualdades que implican las seis funciones trigonométricas estándar. Se supone que los valores dados $theta$ $r,$ $s,$ $x,$ y $y$ todos se encuentran dentro de los límites apropiados para que las expresiones pertinentes a continuación estén bien definidas. Note que "para algunos ${displaystyle kin mathbb {Z} }$ "es sólo otra manera de decir "para algunos enteros $k.$ "

El símbolo ${displaystyle ,iff ,}$ es la igualdad lógica. La expresión "LHS ${displaystyle ,iff ,}$ RHS" indica que o a) El lado izquierdo (es decir, LHS) y el lado derecho (es decir, RHS) son ambos verdadero, o si no (b) el lado izquierdo y el lado derecho son ambos falso; hay no c) (por ejemplo, no posible para que la declaración de LHS sea verdadera y simultáneamente para la declaración de RHS a falso), porque de lo contrario "LHS ${displaystyle ,iff ,}$ RHS" no habría sido escrito (ver esta nota de pie de página para un ejemplo que ilustra este concepto).

Soluciones para funciones trigonométricas elementales
Ecuación	si	Solución (para algunos) ${displaystyle kin mathbb {Z} }$ )	si	Forma ampliada de solución (para algunos) ${displaystyle kin mathbb {Z} }$ )
${displaystyle sin theta =y}$	$iff$	${displaystyle theta =(-1)^{k}arcsin(y)+{phantom {2,}}pi k}$	$iff$	${displaystyle {begin{aligned}theta &={phantom {-}}arcsin(y)+2pi h\&=-arcsin(y)+2pi h+pi end{aligned}}}$
${displaystyle csc theta =r}$	$iff$	${displaystyle theta =(-1)^{k}operatorname {arccsc} (r)+{phantom {2,}}pi k}$	$iff$	${displaystyle {begin{aligned}theta &={phantom {-}}operatorname {arccsc}(y)+2pi h\&=-operatorname {arccsc}(y)+2pi h+pi end{aligned}}}$
${displaystyle cos theta =x}$	$iff$	${displaystyle theta ={phantom {quad ,,}}pm arccos(x)+2,pi k}$	$iff$	${displaystyle {begin{aligned}theta &={phantom {-}}arccos(y)+2pi h\&=-arccos(y)+2pi h{phantom {+pi }}end{aligned}}}$
${displaystyle sec theta =r}$	$iff$	${displaystyle theta ={phantom {quad ,,}}pm ,operatorname {arcsec} (r)+2,pi k}$	$iff$	${displaystyle {begin{aligned}theta &={phantom {-}}operatorname {arcsec}(y)+2pi h\&=-operatorname {arcsec}(y)+2pi h{phantom {+pi }}end{aligned}}}$
${displaystyle tan theta =s}$	$iff$	${displaystyle theta ={phantom {(-1),,}}arctan(s)+{phantom {2,}}pi k}$
${displaystyle cot theta =r}$	$iff$	${displaystyle theta ={phantom {(-1),,,}}operatorname {arccot} (r)+{phantom {2,}}pi k}$

Por ejemplo, si ${displaystyle cos theta =-1}$ entonces ${displaystyle theta =pi +2pi k=-pi +2pi (1+k)}$ para algunos ${displaystyle kin mathbb {Z}.}$ Mientras que si ${displaystyle sin theta =pm 1}$ entonces ${textstyle theta ={frac {pi }{2}}+pi k=-{frac {pi }{2}}+pi (k+1)}$ para algunos ${displaystyle kin mathbb {Z}}$ Donde $k$ será incluso si ${displaystyle sin theta =1}$ y será extraño si ${displaystyle sin theta =-1.}$ Las ecuaciones ${displaystyle sec theta =-1}$ y ${displaystyle csc theta =pm 1}$ tienen las mismas soluciones ${displaystyle cos theta =-1}$ y ${displaystyle sin theta =pm 1,}$ respectivamente. En todas las ecuaciones arriba excepto para aquellos que acaban de resolver (es decir, $sin$ / ${displaystyle csc theta =pm 1}$ y $cos$ / ${displaystyle sec theta =-1}$ ), el entero $k$ en la fórmula de la solución está determinada por $theta$ (para fijo ${displaystyle r,s,x,}$ y $y$ ).

Did you mean:

Detailed example and explanation of the "plus or minus#34; symbol ±

Las soluciones ${displaystyle cos theta =x}$ y ${displaystyle sec theta =x}$ implica el símbolo "más o menos" ${displaystyle ,pm,}$ cuyo significado se aclara ahora. Sólo la solución ${displaystyle cos theta =x}$ será discutido desde el debate ${displaystyle sec theta =x}$ es lo mismo. Nos dan $x$ entre ${displaystyle -1leq xleq 1}$ y sabemos que hay un ángulo $theta$ en algún intervalo que satisfice ${displaystyle cos theta =x.}$ Queremos encontrar esto $theta.$ El cuadro anterior indica que la solución es

{displaystyle ,theta =pm arccos x+2pi k,quad {text{ for some }}kin mathbb {Z} }

${displaystyle ,theta =arccos x+2pi k,}$ para algunos enteros $k,$
o
${displaystyle ,theta =-arccos x+2pi k,}$ para algunos enteros $k.$

Como se mencionó anteriormente, si ${displaystyle ,arccos x=pi ,}$ (que por definición sólo ocurre cuando ${displaystyle x=cos pi =-1}$ ) entonces ambas declaraciones (1) y (2) mantener, aunque con diferentes valores para el entero $k$ Si $K$ es el entero de la declaración (1), que significa que ${displaystyle theta =pi +2pi K}$ sostiene, entonces el entero $k$ para la declaración (2) $K+1$ (porque ${displaystyle theta =-pi +2pi (1+K)}$ ). Sin embargo, si ${displaystyle xneq -1}$ entonces el entero $k$ es único y completamente determinado por $theta.$ Si ${displaystyle ,arccos x=0,}$ (que por definición sólo ocurre cuando ${displaystyle x=cos 0=1}$ entonces ${displaystyle ,pm arccos x=0,}$ (porque ${displaystyle ,+arccos x=+0=0,}$ y ${displaystyle ,-arccos x=-0=0,}$ así como en ambos casos ${displaystyle ,pm arccos x,}$ es igual a ${displaystyle 0}$ ) y por lo tanto las declaraciones (1) y (2) resultan ser idénticas en este caso particular (y por lo tanto ambas sostienen). Habiendo examinado los casos ${displaystyle ,arccos x=0,}$ y ${displaystyle ,arccos x=pi,}$ ahora nos centramos en el caso donde ${displaystyle ,arccos xneq 0,}$ y ${displaystyle ,arccos xneq pi,}$ Asuma esto de ahora en adelante. La solución ${displaystyle cos theta =x}$ todavía

{displaystyle ,theta =pm arccos x+2pi k,quad {text{ for some }}kin mathbb {Z} }

{displaystyle ,arccos xneq 0,}

<math alttext="{displaystyle ,0<arccos x0.arccos x.π π ,{displaystyle ,0 wonrccos x 0pi,} <img alt="{displaystyle ,0<arccos x

exactamente uno

theta

x=0

Todos

theta

{displaystyle ,-pi leq theta leq pi ,}

{displaystyle arccos x=arccos 0={frac {pi }{2}}}

k=0

{displaystyle ,+,}

{displaystyle ,-,}

{displaystyle theta ~=~pm arccos x+2pi k~=~pm left({frac {pi }{2}}right)+2pi (0)~=~pm {frac {pi }{2}}.}

theta

{displaystyle ,pi /2,}

{displaystyle ,-pi /2.}

theta

theta

x

theta =pi /2

x

{displaystyle theta =-pi /2}

Transformar ecuaciones

Las ecuaciones anteriores se pueden transformar usando las identidades de reflexión y desplazamiento:

Transformar ecuaciones por turnos y reflexiones
Argumento: ${displaystyle {underline {;~~~~~~;}}=}$	${displaystyle -theta }$	${displaystyle {frac {pi }{2}}pm theta }$	${displaystyle pi pm theta }$	${displaystyle {frac {3pi }{2}}pm theta }$	${displaystyle 2kpi pm theta}$ ${displaystyle (kin mathbb {Z})}$
${displaystyle sin {underline {;~~~~~~~~~~~~~~;}}=}$	$-sin theta$	${displaystyle {phantom {-}}cos theta }$	${displaystyle mp sin theta }$	${displaystyle -cos theta }$	${displaystyle pm sin theta }$
${displaystyle csc {underline {;~~~~~~~~~~~~~~;}}=}$	${displaystyle -csc theta }$	${displaystyle {phantom {-}}sec theta }$	${displaystyle mp csc theta }$	${displaystyle -sec theta }$	${displaystyle pm csc theta }$
${displaystyle cos {underline {;~~~~~~~~~~~~~~;}}=}$	${displaystyle {phantom {-}}cos theta }$	${displaystyle mp sin theta }$	${displaystyle -cos theta }$	${displaystyle pm sin theta }$	${displaystyle {phantom {-}}cos theta }$
${displaystyle sec {underline {;~~~~~~~~~~~~~~;}}=}$	${displaystyle {phantom {-}}sec theta }$	${displaystyle mp csc theta }$	${displaystyle -sec theta }$	${displaystyle pm csc theta }$	${displaystyle {phantom {-}}sec theta }$
${displaystyle tan {underline {;~~~~~~~~~~~~~~;}}=}$	${displaystyle -tan theta }$	${displaystyle mp cot theta }$	${displaystyle pm tan theta }$	${displaystyle mp cot theta }$	${displaystyle pm tan theta }$
${displaystyle cot {underline {;~~~~~~~~~~~~~~;}}=}$	${displaystyle -cot theta }$	${displaystyle mp tan theta }$	${displaystyle pm cot theta }$	${displaystyle mp tan theta }$	${displaystyle pm cot theta }$

Estas fórmulas implican, en particular, que se cumple lo siguiente:

{displaystyle {begin{aligned}sin theta &=-sin(-theta)&&=-sin(pi +theta)&&={phantom {-}}sin(pi -theta)\&=-cos left({frac {pi }{2}}+theta right)&&={phantom {-}}cos left({frac {pi }{2}}-theta right)&&=-cos left(-{frac {pi }{2}}-theta right)\&={phantom {-}}cos left(-{frac {pi }{2}}+theta right)&&=-cos left({frac {3pi }{2}}-theta right)&&=-cos left(-{frac {3pi }{2}}+theta right)\[0.3ex]cos theta &={phantom {-}}cos(-theta)&&=-cos(pi +theta)&&={phantom {-}}cos(pi -theta)\&={phantom {-}}sin left({frac {pi }{2}}+theta right)&&={phantom {-}}sin left({frac {pi }{2}}-theta right)&&=-sin left(-{frac {pi }{2}}-theta right)\&=-sin left(-{frac {pi }{2}}+theta right)&&=-sin left({frac {3pi }{2}}-theta right)&&={phantom {-}}sin left(-{frac {3pi }{2}}+theta right)\[0.3ex]tan theta &=-tan(-theta)&&={phantom {-}}tan(pi +theta)&&=-tan(pi -theta)\&=-cot left({frac {pi }{2}}+theta right)&&={phantom {-}}cot left({frac {pi }{2}}-theta right)&&={phantom {-}}cot left(-{frac {pi }{2}}-theta right)\&=-cot left(-{frac {pi }{2}}+theta right)&&={phantom {-}}cot left({frac {3pi }{2}}-theta right)&&=-cot left(-{frac {3pi }{2}}+theta right)\[0.3ex]end{aligned}}}

donde intercambiar ${displaystyle sin leftrightarrow csc}$ Swapping ${displaystyle cos leftrightarrow sec}$ y intercambio ${displaystyle tan leftrightarrow cot }$ da las ecuaciones analógicas para ${displaystyle cscsec{text{ and }}cot}$ respectivamente.

Por ejemplo, utilizando la igualdad ${textstyle sin left({frac {pi }{2}}-theta right)=cos theta}$ la ecuación ${displaystyle cos theta =x}$ se puede transformar en ${textstyle sin left({frac {pi }{2}}-theta right)=x,}$ que permite la solución a la ecuación ${displaystyle ;sin varphi =x;}$ (donde) ${textstyle varphi:={frac {pi }{2}}-theta }$ ) para ser utilizado; esa solución es: ${displaystyle varphi =(-1)^{k}arcsin(x)+pi k;{text{ for some }}kin mathbb {Z}}$ que se convierte en:

{displaystyle {frac {pi }{2}}-theta ~=~(-1)^{k}arcsin(x)+pi kquad {text{ for some }}kin mathbb {Z} }

{displaystyle (-1)^{k}=(-1)^{-k}}

{displaystyle h:=-k}

{displaystyle ;cos theta =x;}

{displaystyle theta ~=~(-1)^{h+1}arcsin(x)+pi h+{frac {pi }{2}}quad {text{ for some }}hin mathbb {Z}.}

{displaystyle ;arcsin x={frac {pi }{2}}-arccos x;}

{displaystyle ;arccos x;}

{displaystyle ;arcsin x.;}

Funciones trigonométricas iguales e idénticas

La tabla siguiente muestra cómo dos ángulos $theta$ y $varphi$ debe estar relacionado si sus valores bajo una función trigonométrica dada son iguales o negativos entre sí.


Ecuación	si	Solución (para algunos) ${displaystyle kin mathbb {Z} }$ )	También una solución
${displaystyle {phantom {-}}sin theta =sin varphi }$	$iff$	${displaystyle theta ={phantom {quad }}(-1)^{k}varphi +{phantom {2}}pi k{phantom {+pi }}}$	${displaystyle {phantom {-}}csc theta =csc varphi }$
${displaystyle {phantom {-}}cos theta =cos varphi }$	$iff$	${displaystyle theta ={phantom {-1quad }}pm varphi +2pi k{phantom {+pi }}}$	${displaystyle {phantom {-}}sec theta =sec varphi }$
${displaystyle {phantom {-}}tan theta =tan varphi }$	$iff$	${displaystyle theta ={phantom {(-1)^{k+1}}}varphi +{phantom {2}}pi k{phantom {+pi }}}$	${displaystyle {phantom {-}}cot theta =cot varphi }$
${displaystyle -sin theta =sin varphi }$	$iff$	${displaystyle theta =(-1)^{k+1}varphi +{phantom {2}}pi k{phantom {+pi }}}$	${displaystyle -csc theta =csc varphi }$
${displaystyle -cos theta =cos varphi }$	$iff$	${displaystyle theta ={phantom {-1quad }}pm varphi +2pi k+pi {phantom {+pi }}}$	${displaystyle -sec theta =sec varphi }$
${displaystyle -tan theta =tan varphi }$	$iff$	${displaystyle theta ={phantom {-1quad }}-varphi +{phantom {2}}pi k{phantom {+pi }}}$	${displaystyle -cot theta =cot varphi }$
${displaystyle {begin{aligned}{phantom {-}}left\|sin theta right\|&=left\|sin varphi right\|\{phantom {-}}left\|cos theta right\|&=left\|cos varphi right\|end{aligned}}}$	$iff$	${displaystyle theta ={phantom {-1quad }}pm varphi +{phantom {2}}pi k{phantom {+pi }}}$	${displaystyle {begin{aligned}{phantom {-}}left\|tan theta right\|&=left\|tan varphi right\|\left\|csc theta right\|&=left\|csc varphi right\|\left\|sec theta right\|&=left\|sec varphi right\|\left\|cot theta right\|&=left\|cot varphi right\|end{aligned}}}$

Relaciones entre funciones trigonométricas y funciones trigonométricas inversas

Las funciones trigonométricas de las funciones trigonométricas inversas se tabulan a continuación. Una manera rápida de derivarlos es considerando la geometría de un triángulo recto-ángulo, con un lado de la longitud 1 y otro lado de la longitud $x,$ luego aplicar el teorema pitagórico y las definiciones de las ratios trigonométricas. Vale la pena señalar que para arcsecante y arccosecante, el diagrama asume que $x$ es positivo, y por lo tanto el resultado debe ser corregido mediante el uso de valores absolutos y la operación signum (sgn).

$theta$	$sin(theta)$	$cos(theta)$	$tan(theta)$
$arcsin(x)$	$sin(arcsin(x))=x$	$cos(arcsin(x))={sqrt {1-x^{2}}}$	$tan(arcsin(x))={frac {x}{sqrt {1-x^{2}}}}$
$arccos(x)$	$sin(arccos(x))={sqrt {1-x^{2}}}$	$cos(arccos(x))=x$	$tan(arccos(x))={frac {sqrt {1-x^{2}}}{x}}$
$arctan(x)$	$sin(arctan(x))={frac {x}{sqrt {1+x^{2}}}}$	$cos(arctan(x))={frac {1}{sqrt {1+x^{2}}}}$	$tan(arctan(x))=x$
$operatorname {arccot}(x)$	$sin(operatorname {arccot}(x))={frac {1}{sqrt {1+x^{2}}}}$	$cos(operatorname {arccot}(x))={frac {x}{sqrt {1+x^{2}}}}$	$tan(operatorname {arccot}(x))={frac {1}{x}}$
$operatorname {arcsec}(x)$	${displaystyle sin(operatorname {arcsec}(x))={frac {sqrt {x^{2}-1}}{\|x\|}}}$	$cos(operatorname {arcsec}(x))={frac {1}{x}}$	${displaystyle tan(operatorname {arcsec}(x))=operatorname {sgn}(x){sqrt {x^{2}-1}}}$
$operatorname {arccsc}(x)$	$sin(operatorname {arccsc}(x))={frac {1}{x}}$	${displaystyle cos(operatorname {arccsc}(x))={frac {sqrt {x^{2}-1}}{\|x\|}}}$	${displaystyle tan(operatorname {arccsc}(x))={frac {operatorname {sgn}(x)}{sqrt {x^{2}-1}}}}$

Relaciones entre las funciones trigonométricas inversas

Ángulos complementarios:

{begin{aligned}arccos(x)&={frac {pi }{2}}-arcsin(x)\[0.5em]operatorname {arccot}(x)&={frac {pi }{2}}-arctan(x)\[0.5em]operatorname {arccsc}(x)&={frac {pi }{2}}-operatorname {arcsec}(x)end{aligned}}

Argumentos negativos:

{displaystyle {begin{aligned}arcsin(-x)&=-arcsin(x)\arccos(-x)&=pi -arccos(x)\arctan(-x)&=-arctan(x)\operatorname {arccot}(-x)&=pi -operatorname {arccot}(x)\operatorname {arcsec}(-x)&=pi -operatorname {arcsec}(x)\operatorname {arccsc}(-x)&=-operatorname {arccsc}(x)end{aligned}}}

Argumentos recíprocos:

0\[0.3em]arctan left({frac {1}{x}}right)&=-{frac {pi }{2}}-arctan(x)=operatorname {arccot}(x)-pi ,,{text{ if }}x0\[0.3em]operatorname {arccot} left({frac {1}{x}}right)&={frac {3pi }{2}}-operatorname {arccot}(x)=pi +arctan(x),,{text{ if }}xarccos⁡ ⁡ ()1x)=arcsec⁡ ⁡ ()x)arcsin⁡ ⁡ ()1x)=arccsc⁡ ⁡ ()x)arctan⁡ ⁡ ()1x)=π π 2− − arctan⁡ ⁡ ()x)=arccot⁡ ⁡ ()x),six■0arctan⁡ ⁡ ()1x)=− − π π 2− − arctan⁡ ⁡ ()x)=arccot⁡ ⁡ ()x)− − π π ,six.0arccot⁡ ⁡ ()1x)=π π 2− − arccot⁡ ⁡ ()x)=arctan⁡ ⁡ ()x),six■0arccot⁡ ⁡ ()1x)=3π π 2− − arccot⁡ ⁡ ()x)=π π +arctan⁡ ⁡ ()x),six.0arcsec⁡ ⁡ ()1x)=arccos⁡ ⁡ ()x)arccsc⁡ ⁡ ()1x)=arcsin⁡ ⁡ ()x){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicros}} {fnMicrox} {fnMicrox} {f}f}f}f}fnMicrox} {fnMicrox}f}c}}f}fnMicrox} {f}fnMicrox}fnMicrox}fnMicrox}f}f}fnMicrox}f}fnun}f}fnun}fnun}f}fnun}fnun}f}fnun}fnun}fnMinun}c]fnMinMinMinun}f}fnMin }{2}-arctan(x)=operatorname {arccot}(x),{text{ if }x {0[0.3em]arctan left({frac {1}{x}right)} {frac {pic} }{2}-arctan(x)=operatorname {arccot}(x)-pi ,{text{ if }}x won0\[0.3em]operatorname {arccot} left({frac {1}{x}}}}right) Due={frac {pic {pic}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}][0.3em]operatorname {arccot}left({frac {1}{x}right)}={frac {3pi)} ################################################################################################################################################################################################################################################################0\[0.3em]arctan left({frac {1}{x}}right)&=-{frac {pi }{2}}-arctan(x)=operatorname {arccot}(x)-pi ,,{text{ if }}x0\[0.3em]operatorname {arccot} left({frac {1}{x}}right)&={frac {3pi }{2}}-operatorname {arccot}(x)=pi +arctan(x),,{text{ if }}x

Identidades útiles si solo se tiene un fragmento de una tabla de senos:

{displaystyle {begin{aligned}arccos(x)&=arcsin left({sqrt {1-x^{2}}}right),,{text{ if }}0leq xleq 1{text{ from which you get }}\arccos &left({frac {1-x^{2}}{1+x^{2}}}right)=arcsin left({frac {2x}{1+x^{2}}}right),,{text{ if }}0leq xleq 1\arcsin &left({sqrt {1-x^{2}}}right)={frac {pi }{2}}-operatorname {sgn}(x)arcsin(x)\arccos(x)&={frac {1}{2}}arccos left(2x^{2}-1right),,{text{ if }}0leq xleq 1\arcsin(x)&={frac {1}{2}}arccos left(1-2x^{2}right),,{text{ if }}0leq xleq 1\arcsin(x)&=arctan left({frac {x}{sqrt {1-x^{2}}}}right)\arccos(x)&=arctan left({frac {sqrt {1-x^{2}}}{x}}right)\arctan(x)&=arcsin left({frac {x}{sqrt {1+x^{2}}}}right)\operatorname {arccot}(x)&=arccos left({frac {x}{sqrt {1+x^{2}}}}right)end{aligned}}}

Did you mean:

Whenever the square root of a complex number is used here, we choose the root with the positive real part (or positive imaginary part of the square was negative real).

Un formulario útil que se deriva directamente de la tabla anterior es

{displaystyle arctan left(xright)=arccos left({sqrt {frac {1}{1+x^{2}}}}right),,{text{ if }}xgeq 0}

Se obtiene reconociendo que ${displaystyle cos left(arctan left(xright)right)={sqrt {frac {1}{1+x^{2}}}}=cos left(arccos left({sqrt {frac {1}{1+x^{2}}}}right)right)}$ .

De la fórmula de medio triángulo, ${displaystyle tan left({tfrac {theta }{2}}right)={tfrac {sin(theta)}{1+cos(theta)}}}$ , tenemos:

<math alttext="{displaystyle {begin{aligned}arcsin(x)&=2arctan left({frac {x}{1+{sqrt {1-x^{2}}}}}right)\[0.5em]arccos(x)&=2arctan left({frac {sqrt {1-x^{2}}}{1+x}}right),,{text{ if }}-1arcsin⁡ ⁡ ()x)=2arctan⁡ ⁡ ()x1+1− − x2)arccos⁡ ⁡ ()x)=2arctan⁡ ⁡ ()1− − x21+x),si− − 1.x≤ ≤ 1arctan⁡ ⁡ ()x)=2arctan⁡ ⁡ ()x1+1+x2){displaystyle {begin{aligned}arcsin(x) recur=2arctan left({frac {x}{1+{sqrt {1-x^{2}}}}derecha)[0.5em]arccos(x) sensible=2arctan left({frac {sqrt {1-x^{2}}{1+x}derecha),{text{ if }}}-1Seguidoxleq 1[0.5em]arctan(x) implica=2arctan left({frac] {x}{1+{sqrt {1+x^{2}}}}} {fnunció}}}<img alt="{displaystyle {begin{aligned}arcsin(x)&=2arctan left({frac {x}{1+{sqrt {1-x^{2}}}}}right)\[0.5em]arccos(x)&=2arctan left({frac {sqrt {1-x^{2}}}{1+x}}right),,{text{ if }}-1

Fórmula de suma arcangente

{displaystyle arctan(u)pm arctan(v)=arctan left({frac {upm v}{1mp uv}}right){pmod {pi }},,quad uvneq 1,.}

Esto se deriva de la fórmula de suma tangente

{displaystyle tan(alpha pm beta)={frac {tan(alpha)pm tan(beta)}{1mp tan(alpha)tan(beta)}},,}

al dejar

alpha =arctan(u),,quad beta =arctan(v),.

En cálculo

Derivadas de funciones trigonométricas inversas

Las derivadas para valores complejos de z son las siguientes:

{displaystyle {begin{aligned}{frac {d}{dz}}arcsin(z)&{}={frac {1}{sqrt {1-z^{2}}}};;&z&{}neq -1,+1\{frac {d}{dz}}arccos(z)&{}=-{frac {1}{sqrt {1-z^{2}}}};;&z&{}neq -1,+1\{frac {d}{dz}}arctan(z)&{}={frac {1}{1+z^{2}}};;&z&{}neq -i,+i\{frac {d}{dz}}operatorname {arccot}(z)&{}=-{frac {1}{1+z^{2}}};;&z&{}neq -i,+i\{frac {d}{dz}}operatorname {arcsec}(z)&{}={frac {1}{z^{2}{sqrt {1-{frac {1}{z^{2}}}}}}};;&z&{}neq -1,0,+1\{frac {d}{dz}}operatorname {arccsc}(z)&{}=-{frac {1}{z^{2}{sqrt {1-{frac {1}{z^{2}}}}}}};;&z&{}neq -1,0,+1end{aligned}}}

Solo para valores reales de x:

1\{frac {d}{dx}}operatorname {arccsc}(x)&{}=-{frac {1}{|x|{sqrt {x^{2}-1}}}};;&|x|>1end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">ddxarcsec⁡ ⁡ ()x)=1SilencioxSilenciox2− − 1;SilencioxSilencio■1ddxarccsc⁡ ⁡ ()x)=− − 1SilencioxSilenciox2− − 1;SilencioxSilencio■1{displaystyle {begin{aligned}{frac} [d] {dx}operatorname {arcsec}(x) implica{}={frac {1}{Principio en inglés) {x^{2}}}}; {d}{dx}operatorname {arccsc}(x) implica{}=-{frac {1}{Principe a la vida eterna{sqrt {x^{2}}}};; Una vida útilx confidencial1end{aligned}}1\{frac {d}{dx}}operatorname {arccsc}(x)&{}=-{frac {1}{|x|{sqrt {x^{2}-1}}}};;&|x|>1end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f2385485a94b92758573400c6e2bf5c7466647fd" style="vertical-align: -6.171ex; width:43.645ex; height:13.509ex;"/>

Para una derivación de muestra: si ${displaystyle theta =arcsin(x)}$ , tenemos:

{displaystyle {frac {darcsin(x)}{dx}}={frac {dtheta }{dsin(theta)}}={frac {dtheta }{cos(theta),dtheta }}={frac {1}{cos(theta)}}={frac {1}{sqrt {1-sin ^{2}(theta)}}}={frac {1}{sqrt {1-x^{2}}}}}

Expresión como integrales definidas

Integrar la derivada y fijar el valor en un punto da una expresión para la función trigonométrica inversa como una integral definida:

{displaystyle {begin{aligned}arcsin(x)&{}=int _{0}^{x}{frac {1}{sqrt {1-z^{2}}}},dz;,&|x|&{}leq 1\arccos(x)&{}=int _{x}^{1}{frac {1}{sqrt {1-z^{2}}}},dz;,&|x|&{}leq 1\arctan(x)&{}=int _{0}^{x}{frac {1}{z^{2}+1}},dz;,\operatorname {arccot}(x)&{}=int _{x}^{infty }{frac {1}{z^{2}+1}},dz;,\operatorname {arcsec}(x)&{}=int _{1}^{x}{frac {1}{z{sqrt {z^{2}-1}}}},dz=pi +int _{-x}^{-1}{frac {1}{z{sqrt {z^{2}-1}}}},dz;,&x&{}geq 1\operatorname {arccsc}(x)&{}=int _{x}^{infty }{frac {1}{z{sqrt {z^{2}-1}}}},dz=int _{-infty }^{-x}{frac {1}{z{sqrt {z^{2}-1}}}},dz;,&x&{}geq 1\end{aligned}}}

Cuando x es igual a 1, las integrales con dominios limitados son integrales impropias, pero aún están bien definidas.

Serie infinita

Similar a las funciones sine y cosine, las funciones trigonométricas inversas también se pueden calcular utilizando la serie de potencia, como sigue. Para arcsine, la serie puede derivarse ampliando su derivado, ${textstyle {tfrac {1}{sqrt {1-z^{2}}}}}$ , como serie binomial, e integración de término por término (utilizando la definición integral como arriba). La serie para el arctangente puede derivarse igualmente al expandir su derivado ${textstyle {frac {1}{1+z^{2}}}}$ en una serie geométrica, y aplicando la definición integral anterior (ver serie Leibniz).

{displaystyle {begin{aligned}arcsin(z)&=z+left({frac {1}{2}}right){frac {z^{3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {z^{5}}{5}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {z^{7}}{7}}+cdots \[5pt]&=sum _{n=0}^{infty }{frac {(2n-1)!!}{(2n)!!}}{frac {z^{2n+1}}{2n+1}}\[5pt]&=sum _{n=0}^{infty }{frac {(2n)!}{(2^{n}n!)^{2}}}{frac {z^{2n+1}}{2n+1}},;qquad |z|leq 1end{aligned}}}

{displaystyle arctan(z)=z-{frac {z^{3}}{3}}+{frac {z^{5}}{5}}-{frac {z^{7}}{7}}+cdots =sum _{n=0}^{infty }{frac {(-1)^{n}z^{2n+1}}{2n+1}},;qquad |z|leq 1qquad zneq i,-i}

Serie para las otras funciones trigonométricas inversas se puede dar en términos de éstas según las relaciones dadas anteriormente. Por ejemplo, ${displaystyle arccos(x)=pi /2-arcsin(x)}$ , ${displaystyle operatorname {arccsc}(x)=arcsin(1/x)}$ , y así sucesivamente. Otra serie es dada por:

{displaystyle 2left(arcsin left({frac {x}{2}}right)right)^{2}=sum _{n=1}^{infty }{frac {x^{2n}}{n^{2}{binom {2n}{n}}}}.}

Leonhard Euler encontró una serie para el arcotangente que converge más rápidamente que su serie de Taylor:

{displaystyle arctan(z)={frac {z}{1+z^{2}}}sum _{n=0}^{infty }prod _{k=1}^{n}{frac {2kz^{2}}{(2k+1)(1+z^{2})}}.}

(El término en la suma para n = 0 es el producto vacío, al igual que 1.)

Alternativamente, esto se puede expresar como

{displaystyle arctan(z)=sum _{n=0}^{infty }{frac {2^{2n}(n!)^{2}}{(2n+1)!}}{frac {z^{2n+1}}{(1+z^{2})^{n+1}}}.}

Otra serie para la función arcotangente está dada por

{displaystyle arctan(z)=isum _{n=1}^{infty }{frac {1}{2n-1}}left({frac {1}{(1+2i/z)^{2n-1}}}-{frac {1}{(1-2i/z)^{2n-1}}}right),}

Donde $i=sqrt{-1}$ es la unidad imaginaria.

Fracciones continuas para arcotangente

Dos alternativas a la serie de potencias para arcotangente son estas fracciones continuas generalizadas:

{displaystyle arctan(z)={frac {z}{1+{cfrac {(1z)^{2}}{3-1z^{2}+{cfrac {(3z)^{2}}{5-3z^{2}+{cfrac {(5z)^{2}}{7-5z^{2}+{cfrac {(7z)^{2}}{9-7z^{2}+ddots }}}}}}}}}}={frac {z}{1+{cfrac {(1z)^{2}}{3+{cfrac {(2z)^{2}}{5+{cfrac {(3z)^{2}}{7+{cfrac {(4z)^{2}}{9+ddots }}}}}}}}}}}

El segundo de ellos es válido en el plano complejo de corte. Hay dos cortes, desde −i hasta el punto del infinito, bajando por el eje imaginario, y desde i hasta el punto del infinito, subiendo por el mismo eje. Funciona mejor para números reales que van de −1 a 1. Los denominadores parciales son los números naturales impares y los numeradores parciales (después del primero) son simplemente (nz)², y cada cuadrado perfecto aparece una vez. El primero fue desarrollado por Leonhard Euler; el segundo de Carl Friedrich Gauss utilizando la serie hipergeométrica gaussiana.

Integrales indefinidas de funciones trigonométricas inversas

Para valores reales y complejos de z:

{displaystyle {begin{aligned}int arcsin(z),dz&{}=z,arcsin(z)+{sqrt {1-z^{2}}}+C\int arccos(z),dz&{}=z,arccos(z)-{sqrt {1-z^{2}}}+C\int arctan(z),dz&{}=z,arctan(z)-{frac {1}{2}}ln left(1+z^{2}right)+C\int operatorname {arccot}(z),dz&{}=z,operatorname {arccot}(z)+{frac {1}{2}}ln left(1+z^{2}right)+C\int operatorname {arcsec}(z),dz&{}=z,operatorname {arcsec}(z)-ln left[zleft(1+{sqrt {frac {z^{2}-1}{z^{2}}}}right)right]+C\int operatorname {arccsc}(z),dz&{}=z,operatorname {arccsc}(z)+ln left[zleft(1+{sqrt {frac {z^{2}-1}{z^{2}}}}right)right]+Cend{aligned}}}

De verdad x ≥ 1:

{displaystyle {begin{aligned}int operatorname {arcsec}(x),dx&{}=x,operatorname {arcsec}(x)-ln left(x+{sqrt {x^{2}-1}}right)+C\int operatorname {arccsc}(x),dx&{}=x,operatorname {arccsc}(x)+ln left(x+{sqrt {x^{2}-1}}right)+Cend{aligned}}}

Para todos los x reales que no estén entre -1 y 1:

{displaystyle {begin{aligned}int operatorname {arcsec}(x),dx&{}=x,operatorname {arcsec}(x)-operatorname {sgn}(x)ln left|x+{sqrt {x^{2}-1}}right|+C\int operatorname {arccsc}(x),dx&{}=x,operatorname {arccsc}(x)+operatorname {sgn}(x)ln left|x+{sqrt {x^{2}-1}}right|+Cend{aligned}}}

El valor absoluto es necesario para compensar los valores positivos y negativos de las funciones arcosecante y arcocosecante. La función signum también es necesaria debido a los valores absolutos en las derivadas de las dos funciones, que crean dos soluciones diferentes para valores positivos y negativos de x. Estos se pueden simplificar aún más utilizando las definiciones logarítmicas de las funciones hiperbólicas inversas:

{displaystyle {begin{aligned}int operatorname {arcsec}(x),dx&{}=x,operatorname {arcsec}(x)-operatorname {arcosh} (|x|)+C\int operatorname {arccsc}(x),dx&{}=x,operatorname {arccsc}(x)+operatorname {arcosh} (|x|)+C\end{aligned}}}

El valor absoluto en el argumento de la función arcosh crea una mitad negativa de su gráfica, haciéndola idéntica a la función logarítmica signum que se muestra arriba.

Todas estas antiderivadas se pueden derivar mediante la integración por partes y las formas derivadas simples que se muestran arriba.

Ejemplo

Uso ${displaystyle int u,dv=uv-int v,du}$ (es decir, integración por partes)

{displaystyle {begin{aligned}u&=arcsin(x)&dv&=dx\du&={frac {dx}{sqrt {1-x^{2}}}}&v&=xend{aligned}}}

Entonces

{displaystyle int arcsin(x),dx=xarcsin(x)-int {frac {x}{sqrt {1-x^{2}}}},dx,}

por la simple sustitución ${displaystyle w=1-x^{2}, dw=-2x,dx}$ produce el resultado final:

{displaystyle int arcsin(x),dx=xarcsin(x)+{sqrt {1-x^{2}}}+C}

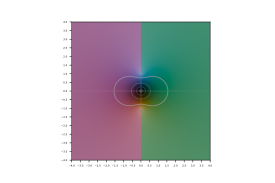
Extensión al plano complejo

Dado que las funciones trigonométricas inversas son funciones analíticas, se pueden extender desde la recta real al plano complejo. Esto da como resultado funciones con múltiples hojas y puntos de ramificación. Una posible forma de definir la extensión es:

{displaystyle arctan(z)=int _{0}^{z}{frac {dx}{1+x^{2}}}quad zneq -i,+i}

donde la parte del eje imaginario que no se encuentra estrictamente entre los puntos de ramificación (−i y +i) es la rama cortada entre la hoja principal y otras hojas. El camino de la integral no debe cruzar un corte de rama. Para z que no está en un corte de rama, una ruta en línea recta de 0 a z es esa ruta. Para z en un corte de rama, el camino debe acercarse desde Re[x] > 0 para el corte de la rama superior y desde Re[x] < 0 para el corte de la rama inferior.

La función arcoseno se puede definir como:

{displaystyle arcsin(z)=arctan left({frac {z}{sqrt {1-z^{2}}}}right)quad zneq -1,+1}

donde (la función de raíz cuadrada tiene su corte a lo largo del eje real negativo y) la parte del eje real que no se encuentra estrictamente entre −1 y +1 es la rama cortada entre la hoja principal de arcsin y otras hojas;

{displaystyle arccos(z)={frac {pi }{2}}-arcsin(z)quad zneq -1,+1}

que tiene el mismo corte que arcsin;

{displaystyle operatorname {arccot}(z)={frac {pi }{2}}-arctan(z)quad zneq -i,i}

que tiene el mismo corte que arctan;

{displaystyle operatorname {arcsec}(z)=arccos left({frac {1}{z}}right)quad zneq -1,0,+1}

donde la parte del eje real entre −1 y +1 inclusive es el corte entre la lámina principal de arcsec y otras láminas;

{displaystyle operatorname {arccsc}(z)=arcsin left({frac {1}{z}}right)quad zneq -1,0,+1}

que tiene el mismo corte que arcsec.

Formas logarítmicas

Estas funciones también se pueden expresar usando logaritmos complejos. Esto extiende sus dominios al plano complejo de forma natural. Las siguientes identidades para los valores principales de las funciones se mantienen en todos los lugares donde se definen, incluso en sus cortes de rama.

{displaystyle {begin{aligned}arcsin(z)&{}=-iln left({sqrt {1-z^{2}}}+izright)=iln left({sqrt {1-z^{2}}}-izright)&{}=operatorname {arccsc} left({frac {1}{z}}right)\[10pt]arccos(z)&{}=-iln left(i{sqrt {1-z^{2}}}+zright)={frac {pi }{2}}-arcsin(z)&{}=operatorname {arcsec} left({frac {1}{z}}right)\[10pt]arctan(z)&{}=-{frac {i}{2}}ln left({frac {i-z}{i+z}}right)=-{frac {i}{2}}ln left({frac {1+iz}{1-iz}}right)&{}=operatorname {arccot} left({frac {1}{z}}right)\[10pt]operatorname {arccot}(z)&{}=-{frac {i}{2}}ln left({frac {z+i}{z-i}}right)=-{frac {i}{2}}ln left({frac {iz-1}{iz+1}}right)&{}=arctan left({frac {1}{z}}right)\[10pt]operatorname {arcsec}(z)&{}=-iln left(i{sqrt {1-{frac {1}{z^{2}}}}}+{frac {1}{z}}right)={frac {pi }{2}}-operatorname {arccsc}(z)&{}=arccos left({frac {1}{z}}right)\[10pt]operatorname {arccsc}(z)&{}=-iln left({sqrt {1-{frac {1}{z^{2}}}}}+{frac {i}{z}}right)=iln left({sqrt {1-{frac {1}{z^{2}}}}}-{frac {i}{z}}right)&{}=arcsin left({frac {1}{z}}right)end{aligned}}}

Generalización

Debido a que todas las funciones trigonométricas inversas generan un ángulo de un triángulo rectángulo, se pueden generalizar usando la fórmula de Euler para formar un triángulo rectángulo en el plano complejo. Algebraicamente, esto nos da:

{displaystyle ce^{itheta }=ccos(theta)+icsin(theta)}

{displaystyle ce^{itheta }=a+ib}

Donde $a$ es el lado adyacente, $b$ es el lado opuesto, y $c$ es la hipotenusa. Desde aquí, podemos resolverlo. $theta$ .

{displaystyle {begin{aligned}e^{ln(c)+itheta }&=a+ib\ln c+itheta &=ln(a+ib)\theta &=operatorname {Im} left(ln(a+ib)right)end{aligned}}}

{displaystyle theta =-iln left({frac {a+ib}{c}}right)}

Simplemente tomar la parte imaginaria funciona para cualquier valor real $a$ y $b$ , pero si $a$ o $b$ es de valor complejo, tenemos que usar la ecuación final para que la parte real del resultado no sea excluida. Puesto que la longitud de la hipotenusa no cambia el ángulo, ignorando la parte real de ${displaystyle ln(a+bi)}$ también elimina $c$ de la ecuación. En la ecuación final, vemos que el ángulo del triángulo en el plano complejo se puede encontrar al introducir las longitudes de cada lado. Al establecer una de las tres partes iguales a 1 y una de las partes restantes iguales a nuestra entrada $z$ , obtenemos una fórmula para una de las funciones de trig inversa, para un total de seis ecuaciones. Debido a que las funciones de trig inversa requieren sólo una entrada, debemos poner el lado final del triángulo en términos de los otros dos usando la relación de Teorema Pythagorean

{displaystyle a^{2}+b^{2}=c^{2}}

La tabla siguiente muestra los valores de a, b, y c para cada una de las funciones de trig inversa y las expresiones equivalentes para $theta$ que resulta de conectar los valores a las ecuaciones anteriores y simplificar.

{displaystyle {begin{aligned}&a&&b&&c&&-iln left({frac {a+ib}{c}}right)&&theta &&theta _{a,bin mathbb {R} }\arcsin(z) &{sqrt {1-z^{2}}}&&z&&1&&-iln left({frac {{sqrt {1-z^{2}}}+iz}{1}}right)&&=-iln left({sqrt {1-z^{2}}}+izright)&&operatorname {Im} left(ln left({sqrt {1-z^{2}}}+izright)right)\arccos(z) &z&&{sqrt {1-z^{2}}}&&1&&-iln left({frac {z+i{sqrt {1-z^{2}}}}{1}}right)&&=-iln left(z+{sqrt {z^{2}-1}}right)&&operatorname {Im} left(ln left(z+{sqrt {z^{2}-1}}right)right)\arctan(z) &1&&z&&{sqrt {1+z^{2}}}&&-iln left({frac {1+iz}{sqrt {1+z^{2}}}}right)&&=-iln left({frac {1+iz}{sqrt {1+z^{2}}}}right)&&operatorname {Im} left(ln left(1+izright)right)\operatorname {arccot}(z) &z&&1&&{sqrt {z^{2}+1}}&&-iln left({frac {z+i}{sqrt {z^{2}+1}}}right)&&=-iln left({frac {z+i}{sqrt {z^{2}+1}}}right)&&operatorname {Im} left(ln left(z+iright)right)\operatorname {arcsec}(z) &1&&{sqrt {z^{2}-1}}&&z&&-iln left({frac {1+i{sqrt {z^{2}-1}}}{z}}right)&&=-iln left({frac {1}{z}}+{sqrt {{frac {1}{z^{2}}}-1}}right)&&operatorname {Im} left(ln left({frac {1}{z}}+{sqrt {{frac {1}{z^{2}}}-1}}right)right)\operatorname {arccsc}(z) &{sqrt {z^{2}-1}}&&1&&z&&-iln left({frac {{sqrt {z^{2}-1}}+i}{z}}right)&&=-iln left({sqrt {1-{frac {1}{z^{2}}}}}+{frac {i}{z}}right)&&operatorname {Im} left(ln left({sqrt {1-{frac {1}{z^{2}}}}}+{frac {i}{z}}right)right)\end{aligned}}}

Para que coincida con la rama principal de las funciones de tronco natural y raíz cuadrada a la rama principal habitual de las funciones de trig inversa, la forma particular de las cuestiones de formulación simplificadas. Las formulaciones dadas en las dos columnas más derechas suponen ${displaystyle operatorname {Im} left(ln zright)in (-pipi ]}$ y ${displaystyle operatorname {Re} left({sqrt {z}}right)geq 0}$ . Para igualar la rama principal ${displaystyle operatorname {Im} left(ln zright)in [0,2pi)}$ y ${displaystyle operatorname {Im} left({sqrt {z}}right)geq 0}$ a la rama principal habitual de las funciones inversas de trig, subtract $2pi$ del resultado $theta$ cuando $pi }" xmlns="http://www.w3.org/1998/Math/MathML">Re⁡ ⁡ ()Silencio Silencio )■π π {displaystyle operatorname {Re} (theta)}pi }" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0217e901ce1260182c0cd0ee56ddaadc995902d1" style="vertical-align: -0.838ex; width:10.073ex; height:2.843ex;"/>$ .

En este sentido, todas las funciones de trig inversa se pueden considerar como casos específicos de la función de registro de valor complejo. Puesto que estas definiciones funcionan para cualquier valor complejo $z$ , las definiciones permiten que los ángulos hiperbólicos como salidas y se pueden utilizar para definir aún más las funciones hiperbólicas inversas. Las pruebas elementales de las relaciones también pueden proceder mediante la expansión a formas exponenciales de las funciones trigonométricas.

Ejemplo de prueba

{displaystyle {begin{aligned}sin(phi)&=z\phi &=arcsin(z)end{aligned}}}

Usando la definición exponencial del pecado, y dejando ${displaystyle xi =e^{iphi },}$

{displaystyle {begin{aligned}z&={frac {e^{iphi }-e^{-iphi }}{2i}}\[10mu]2iz&=xi -{frac {1}{xi }}\[5mu]0&=xi ^{2}-2izxi -1\[5mu]xi &=izpm {sqrt {1-z^{2}}}\[5mu]phi &=-iln left(izpm {sqrt {1-z^{2}}}right)end{aligned}}}

(se elige la rama positiva)

phi =arcsin(z)=-iln left(iz+{sqrt {1-z^{2}}}right)

Gráficos de rueda de colores de **funciones trigonométricas inversas en el plano complejo**

$arcsin(z)$	$arccos(z)$	$arctan(z)$



$operatorname {arccsc}(z)$	$operatorname {arcsec}(z)$	$operatorname {arccot}(z)$

Aplicaciones

Encontrar el ángulo de un triángulo rectángulo

Las funciones trigonométricas inversas son útiles cuando se intenta determinar los dos ángulos restantes de un triángulo rectángulo cuando se conocen las longitudes de los lados del triángulo. Recordando las definiciones de seno y coseno de triángulos rectángulos, se deduce que

{displaystyle theta =arcsin left({frac {text{opposite}}{text{hypotenuse}}}right)=arccos left({frac {text{adjacent}}{text{hypotenuse}}}right).}

A menudo, la hipotenusa es desconocida y tendría que ser calculada antes de usar arcsine o arccosine utilizando el teorema pitagórico: $a^{2}+b^{2}=h^{2}$ Donde $h$ es la longitud de la hipotenusa. El dictador es útil en esta situación, ya que la longitud de la hipotenusa no es necesaria.

theta =arctan left({frac {text{opposite}}{text{adjacent}}}right),.

Por ejemplo, supongamos que un techo cae 8 pies y se extiende 20 pies. El techo forma un ángulo θ con la horizontal, donde θ se puede calcular de la siguiente manera:

theta =arctan left({frac {text{opposite}}{text{adjacent}}}right)=arctan left({frac {text{rise}}{text{run}}}right)=arctan left({frac {8}{20}}right)approx 21.8^{circ },.

En informática e ingeniería

Variante de dos argumentos del arcotangente

Did you mean:

La función atan2 de dos argumentos calcula la arcotangente de y / x dados y y x, pero con un rango de (− $π$ , $π$ ]. En otras palabras, atan2(y, x) es el ángulo entre el eje positivo x de un plano y el punto (x, y) en él, con signo positivo para ángulos en sentido contrario a las agujas del reloj (semiplano superior, y > 0) y signo negativo para los ángulos en el sentido de las agujas del reloj (semiplano inferior, y < 0). Se introdujo por primera vez en muchos lenguajes de programación informática, pero ahora también es común en otros campos de la ciencia y la ingeniería..

En términos de la función estándar arctan, es decir, con un rango de (− $π$ /2, $π$ /2), se puede expresar de la siguiente manera:

0\arctan left({frac {y}{x}}right)+pi &quad ygeq 0,;x<0\arctan left({frac {y}{x}}right)-pi &quad y<0,;x0,;x=0\-{frac {pi }{2}}&quad yatan2⁡ ⁡ ()Sí.,x)={}arctan⁡ ⁡ ()Sí.x)x■0arctan⁡ ⁡ ()Sí.x)+π π Sí.≥ ≥ 0,x.0arctan⁡ ⁡ ()Sí.x)− − π π Sí..0,x.0π π 2Sí.■0,x=0− − π π 2Sí..0,x=0indefinidosSí.=0,x=0{displaystyle operatorname {atan2} (y,x)={begin{cases}arctan left({frac {y}{x}right)}quad x confianza0\\\\ctanleft({frac {y}{x}right)+pi &quad ygeq 0,;x se hizo 0\\\\\\\arctanleft({frac}}}right)-pi >quad > {ccfnMicroccccccccccccccccccccccccH00cccccccccccccccccccccccccccccccccccccH0cccH00cccc }{2} {quad y título, ;x=0\-{frac {pi }{2} {quad Y me dijo: Y=0,;x=0end{cases}0\arctan left({frac {y}{x}}right)+pi &quad ygeq 0,;x<0\arctan left({frac {y}{x}}right)-pi &quad y<0,;x0,;x=0\-{frac {pi }{2}}&quad y

También es igual al valor principal del argumento del número complejo x + iy.

Esta versión limitada de la función anterior también se puede definir usando las fórmulas de medio ángulo tangente de la siguiente manera:

operatorname {atan2} (y,x)=2arctan left({frac {y}{{sqrt {x^{2}+y^{2}}}+x}}right)

siempre que x > 0 o y ≠ 0. Sin embargo, esto falla si se dan x ≤ 0 e y = 0, por lo que la expresión no es adecuada para uso computacional.

El orden de los argumentos anterior (y, x) parece ser el más común y, en particular, se utiliza en estándares ISO como el lenguaje de programación C, pero pocos autores pueden utilizar la convención opuesta (x, y), por lo que se justifica cierta precaución. Estas variaciones se detallan en atan2.

Función arcangente con parámetro de ubicación

En muchas aplicaciones la solución $y$ de la ecuación ${displaystyle x=tan(y)}$ es llegar lo más cerca posible a un valor dado $<math alttext="{displaystyle -infty <eta - - JUEGO JUEGO ... .JUEGO JUEGO {displaystyle -infty } <img alt="-infty <eta$ . La solución adecuada es producida por la función arctangente modificada del parámetro

{displaystyle y=arctan _{eta }(x):=arctan(x)+pi ,operatorname {rni} left({frac {eta -arctan(x)}{pi }}right),.}

La función $operatorname {rni}$ rondas al entero más cercano.

Precisión numérica

Para ángulos cercanos a 0 y $π$ , el arcocoseno está mal condicionado, y lo mismo sucede con el arcoseno para ángulos cercanos a − $π$ /2 y $π$ /2. Por lo tanto, las aplicaciones informáticas deben considerar la estabilidad de las entradas de estas funciones y la sensibilidad de sus cálculos, o utilizar métodos alternativos.

Más resultados...