Funciones elípticas de Jacobi

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Función matemática

En matemáticas, la Funciones elípticas Jacobi son un conjunto de funciones elípticas básicas. Se encuentran en la descripción de la moción de un péndulo (ver también péndulo (mathematics)), así como en el diseño de filtros elípticos electrónicos. Mientras que las funciones trigonométricas se definen con referencia a un círculo, las funciones elípticas de Jacobi son una generalización que se refiere a otras secciones conic, el elipse en particular. La relación con las funciones trigonométricas está contenida en la notación, por ejemplo, por la notación coincidente ${displaystyle operatorname {sn} }$ para $sin$ . Las funciones elípticas de Jacobi se utilizan más a menudo en problemas prácticos que las funciones elípticas de Weierstrass, ya que no requieren nociones de análisis complejo que se definan y/o se entiendan. Fueron introducidos por Carl Gustav Jakob Jacobi (1829). Carl Friedrich Gauss ya había estudiado funciones elípticas especiales de Jacobi en 1797, las funciones elípticas lemniscate en particular, pero su trabajo fue publicado mucho más tarde.

Descripción general

El rectángulo fundamental en el plano complejo $u$

Hay doce funciones elípticas Jacobi denotadas por ${displaystyle operatorname {pq} (u,m)}$ , donde ${displaystyle mathrm {p} }$ y ${displaystyle mathrm {q} }$ cualquiera de las cartas ${displaystyle mathrm {c} }$ , ${displaystyle mathrm {s} }$ , ${displaystyle mathrm {n} }$ , y ${displaystyle mathrm {d} }$ . (Funciones de la forma ${displaystyle operatorname {pp} (u,m)}$ son trivialmente fijados a la unidad para la integridad notacional.) $u$ es el argumento, y $m$ es el parámetro, ambos pueden ser complejos. De hecho, las funciones elípticas de Jacobi son meromorfas en ambos $u$ y $m$ . La distribución de los ceros y los polos en los $u$ - El avión es conocido. Sin embargo, cuestiones de la distribución de los ceros y polos en los $m$ - el avión sigue siendo investigado.

En el plano complejo del argumento $u$ , las doce funciones forman un repetitivo lattice de postes simples y ceros. Dependiendo de la función, un paralelograma repetido, o célula unitaria, tendrá lados de longitud $2K$ o ${displaystyle 4K}$ en el eje real, y ${displaystyle 2K'}$ o ${displaystyle 4K'}$ en el eje imaginario, donde ${displaystyle K=K(m)}$ y ${displaystyle K'=K(1-m)}$ son conocidos como los períodos trimestrales con ${displaystyle K(cdot)}$ ser la integral elíptica del primer tipo. La naturaleza de la célula unitaria puede determinarse al inspeccionar el " rectángulo adiliario" (generalmente un paralelograma), que es un rectángulo formado por el origen $(0,0)$ en una esquina, y ${displaystyle (K,K')}$ como la esquina diagonal opuesta. Como en el diagrama, las cuatro esquinas del rectángulo auxiliar se llaman ${displaystyle mathrm {s} }$ , ${displaystyle mathrm {c} }$ , ${displaystyle mathrm {d} }$ , y ${displaystyle mathrm {n} }$ , yendo en sentido contrario desde el origen. La función ${displaystyle operatorname {pq} (u,m)}$ tendrá un cero en el ${displaystyle mathrm {p} }$ esquina y un poste en el ${displaystyle mathrm {q} }$ esquina. Las doce funciones corresponden a las doce maneras de organizar estos polos y ceros en las esquinas del rectángulo.

Cuando el argumento $u$ y parámetro $m$ son reales, con $<math alttext="{displaystyle 0<m0.m.1{displaystyle 0 realizadasm <img alt="{displaystyle 0<m$ , $K$ y $K'$ será real y el paralelograma auxiliar será de hecho un rectángulo, y las funciones elípticas de Jacobi serán valoradas en la línea real.

Puesto que las funciones elípticas de Jacob son doblemente periódicas en $u$ , ellos factor a través de un torus – en efecto, su dominio se puede tomar para ser un torus, así como cosine y sine están en efecto definidos en un círculo. En lugar de tener sólo un círculo, ahora tenemos el producto de dos círculos, uno real y el otro imaginario. El plano complejo puede ser reemplazado por un toro complejo. La circunferencia del primer círculo es ${displaystyle 4K}$ y el segundo ${displaystyle 4K'}$ , donde $K$ y $K'$ son los períodos trimestrales. Cada función tiene dos ceros y dos polos en posiciones opuestas en el torus. Entre los puntos ${displaystyle 0}$ , $K$ , ${displaystyle K+iK'}$ , ${displaystyle iK'}$ hay un cero y un poste.

Las funciones elípticas jacobianas son entonces funciones meromórficas doblemente periódicas que satisfacen las siguientes propiedades:

Hay un simple cero en la esquina ${displaystyle mathrm {p} }$ , y un simple poste en la esquina ${displaystyle mathrm {q} }$ .
El número complejo ${displaystyle mathrm {p} -mathrm {q} }$ es igual a la mitad del período de la función ${displaystyle operatorname {pq} u}$ ; es decir, la función ${displaystyle operatorname {pq} u}$ es periódica en la dirección ${displaystyle operatorname {pq} }$ , con el período ${displaystyle 2(mathrm {p} -mathrm {q})}$ . La función ${displaystyle operatorname {pq} u}$ es también periódica en las otras dos direcciones ${displaystyle mathrm {pp} '}$ y ${displaystyle mathrm {pq} '}$ , con períodos tales que ${displaystyle mathrm {p} -mathrm {p} '}$ y ${displaystyle mathrm {p} -mathrm {q} '}$ son períodos trimestrales.

Función elíptica Jacobi

{displaystyle operatorname {sn} }

Función elíptica Jacobi

{displaystyle operatorname {cn} }

Función elíptica Jacobi

{displaystyle operatorname {dn} }

Función elíptica Jacobi

{displaystyle operatorname {sc} }

Parcelas de cuatro Funciones Elípticas Jacobi en el plano complejo de

u

, ilustrando su doble comportamiento periódico. Imágenes generadas usando una versión del método de coloración de dominio. Todos tienen valores

{displaystyle k={sqrt {m}}}

iguales

{displaystyle 0.8}

Notación

Las funciones elípticas se pueden dar en una variedad de notaciones, que pueden hacer que el sujeto sea innecesariamente confuso. Las funciones elípticas son funciones de dos variables. La primera variable se puede dar en términos de la amplitud $varphi$ , o más comúnmente, en términos de $u$ dado abajo. La segunda variable se puede dar en términos de la parámetro $m$ , o como modulo elíptico $k$ , donde ${displaystyle k^{2}=m}$ , o en términos de ángulo modular $alpha$ , donde ${displaystyle m=sin ^{2}alpha }$ . Los complementos de $k$ y $m$ se definen como ${displaystyle m'=1-m}$ y ${textstyle k'={sqrt {m'}}}$ . Estos cuatro términos se utilizan a continuación sin comentario para simplificar varias expresiones.

Las doce funciones elípticas Jacobi generalmente se escriben como ${displaystyle operatorname {pq} (u,m)}$ Donde ${displaystyle mathrm {p} }$ y ${displaystyle mathrm {q} }$ cualquiera de las cartas ${displaystyle mathrm {c} }$ , ${displaystyle mathrm {s} }$ , ${displaystyle mathrm {n} }$ , y ${displaystyle mathrm {d} }$ . Funciones de la forma ${displaystyle operatorname {pp} (u,m)}$ son trivialmente fijados a la unidad para la integridad notacional. Las funciones “major” generalmente se toman ${displaystyle operatorname {cn} (u,m)}$ , ${displaystyle operatorname {sn} (u,m)}$ y ${displaystyle operatorname {dn} (u,m)}$ de las cuales se pueden derivar todas las demás funciones y las expresiones se escriben a menudo únicamente en términos de estas tres funciones, sin embargo, varias simetrías y generalizaciones se expresan más convenientemente utilizando el conjunto completo. (Esta notación se debe a Gudermann y Glaisher y no es la notación original de Jacobi.)

A lo largo de este artículo, ${displaystyle operatorname {pq} (u,t^{2})=operatorname {pq} (u;t)}$ .

Las funciones están relacionadas notacionalmente entre sí mediante la regla de multiplicación: (argumentos suprimidos)

{displaystyle operatorname {pq} cdot operatorname {p'q'} =operatorname {pq'} cdot operatorname {p'q} }

de donde se pueden derivar otras relaciones comúnmente utilizadas:

{displaystyle {frac {operatorname {pr} }{operatorname {qr} }}=operatorname {pq} }

{displaystyle operatorname {pr} cdot operatorname {rq} =operatorname {pq} }

{displaystyle {frac {1}{operatorname {qp} }}=operatorname {pq} }

La regla de multiplicación se deriva inmediatamente de la identificación de las funciones elípticas con las funciones theta de Neville

{displaystyle operatorname {pq} (u,m)={frac {theta _{operatorname {p} }(u,m)}{theta _{operatorname {q} }(u,m)}}}

Tenga en cuenta también que:

{displaystyle K(m)=K(k^{2})=int _{0}^{1}{frac {dt}{sqrt {(1-t^{2})(1-mt^{2})}}}=int _{0}^{1}{frac {dt}{sqrt {(1-t^{2})(1-k^{2}t^{2})}}}.}

Definición en términos de inversas de integrales elípticas

Existe una definición, relativa a las funciones elípticas al inverso de la incompleta integral elíptica del primer tipo. Estas funciones toman los parámetros $u$ y $m$ como insumos. El $varphi$ que satisfice

{displaystyle u=int _{0}^{varphi }{frac {mathrm {d} theta }{sqrt {1-msin ^{2}theta }}}}

se llama amplitud de Jacobi:

{displaystyle operatorname {am} (u,m)=varphi.}

En este marco, el seno elíptico sn u (latín: sinus amplitudinis) viene dado por

{displaystyle operatorname {sn} (u,m)=sin operatorname {am} (u,m)}

y el coseno elíptico cn u (latín: cosinus amplitudinis) está dado por

{displaystyle operatorname {cn} (u,m)=cos operatorname {am} (u,m)}

Did you mean:

and the delta amplitude d u (Latini>delta amplitudes)

{displaystyle operatorname {dn} (u,m)={frac {mathrm {d} }{mathrm {d} u}}operatorname {am} (u,m).}

En lo anterior, el valor $m$ es un parámetro libre, generalmente tomado para ser real ${displaystyle 0leq mleq 1}$ , y por lo tanto las funciones elípticas se pueden considerar como dadas por dos variables, $u$ y el parámetro $m$ . Las nueve funciones elípticas restantes se construyen fácilmente a partir de las tres anteriores (en inglés) ${displaystyle operatorname {sn} }$ , ${displaystyle operatorname {cn} }$ , ${displaystyle operatorname {dn} }$ ), y se dan en una sección abajo.

En el entorno más general, ${displaystyle operatorname {am} (u,m)}$ es una función multivalorada (en $u$ ) con infinitamente muchos puntos de rama logarítmica (las ramas difieren por múltiplos enteros de $2pi$ ), es decir, los puntos ${displaystyle 2sK(m)+(4t+1)K(1-m)i}$ y ${displaystyle 2sK(m)+(4t+3)K(1-m)i}$ Donde ${displaystyle s,tin mathbb {Z} }$ . Esta función multivalorada se puede hacer de un solo valor al cortar el plano complejo a lo largo de los segmentos de línea que unen estos puntos de rama (el corte se puede hacer de manera no equivalente, dando funciones no equivalentes de valor único), haciendo así ${displaystyle operatorname {am} (u,m)}$ analytic en todas partes excepto en los cortes de rama. En cambio, ${displaystyle sin operatorname {am} (u,m)}$ y otras funciones elípticas no tienen puntos de rama, dan valores consistentes para cada rama de ${displaystyle operatorname {am} }$ , y son meromorfos en todo el plano complejo. Puesto que cada función elíptica es meromorfa en todo el plano complejo (por definición), ${displaystyle operatorname {am} (u,m)}$ (cuando se considera una función de valor único) no es una función elíptica.

Sin embargo, la inversión integral arriba define una función única de valor real-analítica en un barrio real de $u=0$ si $m$ es real. Hay una continuación analítica única de esta función de ese vecindario a ${displaystyle uin mathbb {R} }$ . La continuación analítica de esta función es periódica en $u$ si $1}" xmlns="http://www.w3.org/1998/Math/MathML">m■1{displaystyle m]1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7f27527902d05e4c32bcbe28d425d7790f8ae191" style="vertical-align: -0.338ex; width:6.301ex; height:2.176ex;"/>$ (con el período mínimo ${displaystyle 4K(1/m)/{sqrt {m}}}$ ), y es denotado por ${displaystyle operatorname {am} (u,m)}$ en el resto de este artículo.

Jacobi también introdujo la función coamplitud:

{displaystyle operatorname {coam} (u,m)=operatorname {am} (K(m)-u,m)}

La función Jacobi épsilon se puede definir como

{displaystyle {mathcal {E}}(u,m)=int _{0}^{u}operatorname {dn} ^{2}(t,m),mathrm {d} t}

y relaciona la incompleta integral elíptica del primer tipo con la incompleta integral elíptica del segundo tipo (con parámetro $m$ ):

{displaystyle E(varphim)={mathcal {E}}(F(varphim),m).}

La función epsilon de Jacobi no es una función elíptica. Sin embargo, a diferencia de la amplitud y coamplitud Jacobi, la función epsilon Jacobi es meromorfa en todo el plano complejo (en ambos $u$ y $m$ ).

La función Jacobi zn está definida por

{displaystyle operatorname {zn} (u,m)=int _{0}^{u}left(operatorname {dn} (t,m)^{2}-{frac {E(m)}{K(m)}}right),mathrm {d} t.}

Es una función periódica cantada que es meromorfa $u$ . Su período mínimo es ${displaystyle 2K(m)}$ . Está relacionado con la función Jacobi zeta por ${displaystyle Z(varphim)=operatorname {zn} (F(varphim),m).}$

Note que cuando ${displaystyle varphi =pi /2}$ , eso $u$ entonces es igual al trimestre $K$ .

Definición como trigonometría: la elipse de Jacobi

${displaystyle cos varphisin varphi }$ se definen en el círculo de la unidad, con radio r= 1 y ángulo ${displaystyle varphi =}$ longitud de arco del círculo de unidad medido desde el positivo x-Eje. Del mismo modo, las funciones elípticas de Jacobi se definen en el elipse de la unidad, con a1. Let

1,\&m=1-{frac {1}{b^{2}}},quad 0<mx2+Sí.2b2=1,b■1,m=1− − 1b2,0.m.1,x=r#⁡ ⁡ φ φ ,Sí.=rpecado⁡ ⁡ φ φ {displaystyle {begin{aligned} {y} {y}{b^{2}}=1,quad b título 1,\\c=1-{1}{b^{2}}}quad 0 se hizo,\\cccccccccs varphiend{aligned}}1,\&m=1-{frac {1}{b^{2}}},quad 0<m

entonces:

{displaystyle r(varphim)={frac {1}{sqrt {1-msin ^{2}varphi }}},.}

Para cada ángulo $varphi$ el parámetro

{displaystyle u=u(varphim)=int _{0}^{varphi }r(thetam),dtheta }

(la incompleta integral elíptica del primer tipo) es computada. En el círculo de la unidad ( $a=b=1$ ), $u$ Sería una longitud de arco. La cantidad ${displaystyle u[varphik]=u(varphik^{2})}$ está relacionado con la integral elíptica incompleta del segundo tipo (con módulo) $k$ ) by

{displaystyle u[varphik]={frac {1}{sqrt {1-k^{2}}}}left({frac {1+{sqrt {1-k^{2}}}}{2}}operatorname {E} left(varphi +arctan left({sqrt {1-k^{2}}}tan varphi right),{frac {1-{sqrt {1-k^{2}}}}{1+{sqrt {1-k^{2}}}}}right)-operatorname {E} (varphik)+{frac {k^{2}sin varphi cos varphi }{2{sqrt {1-k^{2}sin ^{2}varphi }}}}right),}

y por lo tanto está relacionado con la longitud del arco de una elipse. Vamos ${displaystyle P=(x,y)=(rcos varphirsin varphi)}$ ser un punto en la elipse, y dejar ${displaystyle P'=(x',y')=(cos varphisin varphi)}$ ser el punto donde el círculo de la unidad interseca la línea entre $P$ y el origen $O$ . Luego las relaciones familiares del círculo de la unidad:

{displaystyle x'=cos varphiquad y'=sin varphi }

leer la elipse:

{displaystyle x'=operatorname {cn} (u,m),quad y'=operatorname {sn} (u,m).}

Así que las proyecciones del punto de intersección $P'$ de la línea ${displaystyle OP}$ con el círculo de la unidad en x- y Sí.- los ejes son simplemente ${displaystyle operatorname {cn} (u,m)}$ y ${displaystyle operatorname {sn} (u,m)}$ . Estas proyecciones pueden interpretarse como 'definición como trigonometría'. En resumen:

{displaystyle operatorname {cn} (u,m)={frac {x}{r(varphim)}},quad operatorname {sn} (u,m)={frac {y}{r(varphim)}},quad operatorname {dn} (u,m)={frac {1}{r(varphim)}}.}

Para el $x$ y $y$ valor del punto $P$ con $u$ y parámetro $m$ obtenemos, después de insertar la relación:

{displaystyle r(varphim)={frac {1}{operatorname {dn} (u,m)}}}

en: ${displaystyle x=r(varphim)cos(varphi),y=r(varphim)sin(varphi)}$ que:

{displaystyle x={frac {operatorname {cn} (u,m)}{operatorname {dn} (u,m)}},quad y={frac {operatorname {sn} (u,m)}{operatorname {dn} (u,m)}}.}

Las últimas relaciones para x- y Sí.-coordinados de puntos sobre el elipse de la unidad pueden considerarse como generalización de las relaciones ${displaystyle x=cos varphiy=sin varphi }$ para las coordenadas de puntos en el círculo de unidad.

La tabla siguiente resume las expresiones para todas las funciones elípticas Jacobi pq(u,m) en las variables (x,Sí.,r) y (φ,dn) con ${textstyle r={sqrt {x^{2}+y^{2}}}}$

Jacobi elliptic functions pq[u,m] como funciones de {x,*Sí.*,rY...φ,dn}
		q
		c	s	n	d
p
	c	1	${displaystyle x/y=cot(varphi)}$	${displaystyle x/r=cos(varphi)}$	${displaystyle x=cos(varphi)/operatorname {dn} }$
	s	${displaystyle y/x=tan(varphi)}$	1	${displaystyle y/r=sin(varphi)}$	${displaystyle y=sin(varphi)/operatorname {dn} }$
	n	${displaystyle r/x=sec(varphi)}$	${displaystyle r/y=csc(varphi)}$	1	${displaystyle r=1/operatorname {dn} }$
	d	${displaystyle 1/x=sec(varphi)operatorname {dn} }$	${displaystyle 1/y=csc(varphi)operatorname {dn} }$	${displaystyle 1/r=operatorname {dn} }$	1

Definición en términos de funciones theta de Jacobi

Descripción de la función theta de Jacobi

Equivalentemente, las funciones elípticas de Jacobi se pueden definir en términos de sus funciones theta. Si abreviamos ${displaystyle vartheta _{00}(0;q)}$ como ${displaystyle vartheta _{00}(q)}$ , y ${displaystyle vartheta _{01}(0;q),vartheta _{10}(0;q),vartheta _{11}(0;q)}$ respectivamente ${displaystyle vartheta _{01}(q),vartheta _{10}(q),vartheta _{11}(q)}$ (theta constantes) entonces la función theta modulus elíptico k es ${displaystyle k={biggl {}{vartheta _{10}[q(k)] over vartheta _{00}[q(k)]}{biggr }}^{2}}$ . Definimos la nome como $q=exp(pi itau)$ en relación con la relación período. Tenemos

{displaystyle {begin{aligned}operatorname {sn} (u;k)&=-{frac {vartheta _{00}[q(k)],vartheta _{11}[udiv {bar {K}}(k);,q(k)]}{vartheta _{10}[q(k)],vartheta _{01}[udiv {bar {K}}(k);,q(k)]}}\[7pt]operatorname {cn} (u;k)&={frac {vartheta _{01}[q(k)],vartheta _{10}[udiv {bar {K}}(k);,q(k)]}{vartheta _{10}[q(k)],vartheta _{01}[udiv {bar {K}}(k);,q(k)]}}\[7pt]operatorname {dn} (u;k)&={frac {vartheta _{01}[q(k)],vartheta _{00}[udiv {bar {K}}(k);,q(k)]}{vartheta _{00}[q(k)],vartheta _{01}[udiv {bar {K}}(k);,q(k)]}}end{aligned}}}

Donde ${displaystyle {bar {K}}(k)={frac {2}{pi }},K(k)}$ y ${displaystyle q=exp[-pi ,K'(k)/K(k)]}$ .

Edmund Whittaker y George Watson definieron las funciones theta de Jacobi de esta manera en su libro de texto Un curso de análisis moderno:

{displaystyle vartheta _{00}(v;w)=prod _{n=1}^{infty }(1-w^{2n})[1+2cos(2v)w^{2n-1}+w^{4n-2}]}

{displaystyle vartheta _{01}(v;w)=prod _{n=1}^{infty }(1-w^{2n})[1-2cos(2v)w^{2n-1}+w^{4n-2}]}

{displaystyle vartheta _{10}(v;w)=2w^{1/4}cos(v)prod _{n=1}^{infty }(1-w^{2n})[1+2cos(2v)w^{2n}+w^{4n}]}

{displaystyle vartheta _{11}(v;w)=-2w^{1/4}sin(v)prod _{n=1}^{infty }(1-w^{2n})[1-2cos(2v)w^{2n}+w^{4n}]}

Función Jacobi zn

La función Jacobi zn también se puede expresar mediante funciones theta:

{displaystyle {begin{aligned}operatorname {zn} (u;k)&={frac {pi }{2K}}{frac {vartheta _{01}'[udiv {bar {K}}(k);,q(k)]}{vartheta _{01}[udiv {bar {K}}(k);,q(k)]}}\&={frac {pi }{2K}}{frac {vartheta _{00}'[udiv {bar {K}}(k);,q(k)]}{vartheta _{00}[udiv {bar {K}}(k);,q(k)]}}+k^{2}{frac {operatorname {sn} (u;k)operatorname {cn} (u;k)}{operatorname {dn} (u;k)}}\&={frac {pi }{2K}}{frac {vartheta _{10}'[udiv {bar {K}}(k);,q(k)]}{vartheta _{10}[udiv {bar {K}}(k);,q(k)]}}+{frac {operatorname {dn} (u;k)operatorname {sn} (u;k)}{operatorname {cn} (u;k)}}\&={frac {pi }{2K}}{frac {vartheta _{11}'[udiv {bar {K}}(k);,q(k)]}{vartheta _{11}[udiv {bar {K}}(k);,q(k)]}}-{frac {operatorname {cn} (u;k)operatorname {dn} (u;k)}{operatorname {sn} (u;k)}}end{aligned}}}

Donde $'$ denota el derivado parcial con respecto a la entrada del soporte izquierdo:

{displaystyle vartheta '_{00}(v;w)={frac {partial }{partial v}}vartheta _{00}(v;w)}

{displaystyle vartheta '_{01}(v;w)={frac {partial }{partial v}}vartheta _{01}(v;w)}

etc.

La siguiente definición de la función Jacobi zn es idéntica a las fórmulas ahora mencionadas:

{displaystyle {text{zn}}(u;k)=sum _{n=1}^{infty }{frac {2pi K(k)^{-1}sin[pi K(k)^{-1}u]q(k)^{2n-1}}{1-2cos[pi K(k)^{-1}u]q(k)^{2n-1}+q(k)^{4n-2}}}}

De forma sucesiva la amplitud seno sn se puede generar de la siguiente manera:

{displaystyle operatorname {sn} (u;k)={frac {2{operatorname {zn} ({tfrac {1}{2}}u;k)+operatorname {zn} [K(k)-{tfrac {1}{2}}u;k]}}{k^{2}+{operatorname {zn} ({tfrac {1}{2}}u;k)+operatorname {zn} [K(k)-{tfrac {1}{2}}u;k]}^{2}}}}

Comparación entre sumas y productos

La integral elíptica reducida de primer tipo se definirá nuevamente de la siguiente manera:

{displaystyle {bar {K}}(varepsilon)={frac {2}{pi }}K(varepsilon)}

Y el nomo elíptico reducido se definirá siguiendo este patrón:

{displaystyle {bar {q}}(varepsilon)={sqrt[{4}]{varepsilon ^{-2}q(varepsilon)}}}

Los hermanos Peter y Jonathan Borwein también dieron estas dos fórmulas siguientes para la amplitud seno en su trabajo π y el AGM en la página 60 y siguientes:

${displaystyle operatorname {sn} (u;k)=,{frac {4}{{bar {K}}(k)}},{bar {q}}(k)^{2}sin[udiv {bar {K}}(k)]sum _{n=1}^{infty }{frac {q(k)^{n-1}[1+q(k)^{2n-1}]}{1-2q(k)^{2n-1}cos[2udiv {bar {K}}(k)]+q(k)^{4n-2}}}}$
${displaystyle operatorname {sn} (u;k)=2,{bar {q}}(k)sin[udiv {bar {K}}(k)]prod _{n=1}^{infty }{frac {1-2q(k)^{2n}cos[2udiv {bar {K}}(k)]+q(k)^{4n}}{1-2q(k)^{2n-1}cos[2udiv {bar {K}}(k)]+q(k)^{4n-2}}}}$

Esta fórmula que define, que resulta directamente de la sustitución interna ${displaystyle zrightarrow K(k)-z}$ , se aplica analógicamente a la función cd:

${displaystyle operatorname {cd} (u;k)=,{frac {4}{{bar {K}}(k)}},{bar {q}}(k)^{2}cos[udiv {bar {K}}(k)]sum _{n=1}^{infty }{frac {q(k)^{n-1}[1+q(k)^{2n-1}]}{1+2q(k)^{2n-1}cos[2udiv {bar {K}}(k)]+q(k)^{4n-2}}}}$
${displaystyle operatorname {cd} (u;k)=2,{bar {q}}(k)cos[udiv {bar {K}}(k)]prod _{n=1}^{infty }{frac {1+2q(k)^{2n}cos[2udiv {bar {K}}(k)]+q(k)^{4n}}{1+2q(k)^{2n-1}cos[2udiv {bar {K}}(k)]+q(k)^{4n-2}}}}$

Did you mean:

These formulas are based on Whittaker and Watson 's definition of theta non-zero value functions.

Estas fórmulas se aplican a la amplitud del coseno:

${displaystyle operatorname {cn} (u;k)=,{frac {4}{{bar {K}}(k)}},{bar {q}}(k)^{2}cos[udiv {bar {K}}(k)]sum _{n=1}^{infty }{frac {(-1)^{n+1}q(k)^{n-1}[1-q(k)^{2n-1}]}{1-2q(k)^{2n-1}cos[2udiv {bar {K}}(k)]+q(k)^{4n-2}}}}$
${displaystyle operatorname {cn} (u;k)=2,{sqrt[{4}]{1-k^{2}}},{bar {q}}(k)cos[udiv {bar {K}}(k)]prod _{n=1}^{infty }{frac {1+2q(k)^{2n}cos[2udiv {bar {K}}(k)]+q(k)^{4n}}{1-2q(k)^{2n-1}cos[2udiv {bar {K}}(k)]+q(k)^{4n-2}}}}$

Según las fórmulas del producto Whittaker-Watson, esta fórmula también se aplica a la función de amplitud delta:

{displaystyle operatorname {dn} (u;k)={sqrt[{4}]{1-k^{2}}}prod _{n=1}^{infty }{frac {1+2cos[2udiv {bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{1-2cos[2udiv {bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}}}

Con una suma secante hiperbólica es posible una definición para Delta Amplitudinis:

{displaystyle operatorname {dn} (z;k)={frac {pi }{2K({sqrt {1-k^{2}}})}}sum _{n=-infty }^{infty }operatorname {sech} {bigl {}pi K({sqrt {1-k^{2}}})^{-1}{bigl [}K(k)n+{tfrac {1}{2}}z{bigr ]}{bigr }}}

El nomo elíptico y sus series

Nodo elíptica integral y elíptica

(feminine)

Puesto que las funciones Jacobi se definen en términos del módulo elíptico $k(tau)$ , tenemos que invertir esto y encontrar $tau$ en términos de $k$ . Comenzamos desde $k'={sqrt {1-k^{2}}}$ , el módulo complementario. Como función $tau$ Lo es

{displaystyle k'(tau)={sqrt {1-k^{2}}}={biggl {}{vartheta _{01}[q(k)] over vartheta _{00}[q(k)]}{biggr }}^{2}}

Definamos el nomo elíptico y la integral elíptica completa de primer tipo:

{displaystyle q(k)=exp {biggl [}-pi {frac {K({sqrt {1-k^{2}}})}{K(k)}}{biggr ]}}

Estas son dos definiciones idénticas de la integral elíptica completa del primer tipo:

{displaystyle K(k)=int _{0}^{pi /2}{frac {1}{sqrt {1-k^{2}sin(varphi)^{2}}}}partial varphi }

{displaystyle K(k)={frac {pi }{2}}sum _{a=0}^{infty }{frac {[(2a)!]^{2}}{16^{a}(a!)^{4}}}k^{2a}}

Did you mean:

An identical definition of the nome function can be produced by using a series. Following function has this identity:

{displaystyle {frac {1-{sqrt[{4}]{1-k^{2}}}}{1+{sqrt[{4}]{1-k^{2}}}}}={frac {vartheta _{00}[q(k)]-vartheta _{01}[q(k)]}{vartheta _{00}[q(k)]+vartheta _{01}[q(k)]}}={biggl [}sum _{n=1}^{infty }2,q(k)^{(2n-1)^{2}}{biggr ]}{biggl [}1+sum _{n=1}^{infty }2,q(k)^{4n^{2}}{biggr ]}^{-1}}

Puesto que podemos reducir al caso donde la parte imaginaria $tau$ es mayor o igual a ${sqrt {3}}/2$ (ver grupo modular), podemos asumir el valor absoluto $q$ es menor o igual a ${displaystyle exp(-pi {sqrt {3}}/2)approx 0.0658}$ ; para valores tan pequeños la serie anterior converge muy rápidamente y fácilmente nos permite encontrar el valor adecuado para $q$ . Resolviendo esta función después de q obtenemos este resultado:

{displaystyle q(k)=sum _{n=1}^{infty }{frac {{text{Sc}}(n)}{2^{4n-3}}}{biggl (}{frac {1-{sqrt[{4}]{1-k^{2}}}}{1+{sqrt[{4}]{1-k^{2}}}}}{biggr)}^{4n-3}=k^{2}{biggl {}{frac {1}{2}}+{biggl [}sum _{n=1}^{infty }{frac {{text{Sc}}(n+1)}{2^{4n+1}}}k^{2n}{biggr ]}{biggr }}^{4}}

Esta tabla muestra los números de la secuencia entera de Schwarz A002103 con precisión:

Sc(1)	Sc(2)	Sc(3)	Sc(4)	Sc(5)	Sc(6)	Sc(7)	Sc(8)
1	2	15	150	1707	20910	268616	3567400

Secuencia entera de Kneser

El matemático alemán Adolf Kneser investigó la secuencia entera de la razón del período elíptico en su ensayo Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen y demostró que la función generadora de esta secuencia es una elíptica. función. Otro matemático llamado Robert Fricke analizó esta secuencia de números enteros en su ensayo Die elliptischen Funktionen und ihre Anwendungen y describió los métodos de cálculo precisos utilizando esta secuencia mencionada. La secuencia entera de Kneser Kn(n) se puede construir de esta manera:

${displaystyle {text{Kn}}(2n)=2^{4n-3}{binom {4n}{2n}}+sum _{m=1}^{n}4^{2n-2m}{binom {4n}{2n-2m}}{text{Kn}}(m)}$
${displaystyle {text{Kn}}(2n+1)=2^{4n-1}{binom {4n+2}{2n+1}}+sum _{m=1}^{n}4^{2n-2m+1}{binom {4n+2}{2n-2m+1}}{text{Kn}}(m)}$

Ejemplos ejecutados:

${displaystyle {text{Kn}}(2)=2times 6+1times {color {cornflowerblue}1}={color {cornflowerblue}13}}$
${displaystyle {text{Kn}}(3)=8times 20+24times {color {cornflowerblue}1}={color {cornflowerblue}184}}$
${displaystyle {text{Kn}}(4)=32times 70+448times {color {cornflowerblue}1}+1times {color {cornflowerblue}13}={color {cornflowerblue}2701}}$
${displaystyle {text{Kn}}(5)=128times 252+7680times {color {cornflowerblue}1}+40times {color {cornflowerblue}13}={color {cornflowerblue}40456}}$
${displaystyle {text{Kn}}(6)=512times 924+126720times {color {cornflowerblue}1}+1056times {color {cornflowerblue}13}+1times {color {cornflowerblue}184}={color {cornflowerblue}613720}}$
${displaystyle {text{Kn}}(7)=2048times 3432+2050048times {color {cornflowerblue}1}+23296times {color {cornflowerblue}13}+56times {color {cornflowerblue}184}={color {cornflowerblue}9391936}}$

La secuencia de Kneser aparece en la serie de Taylor de la razón de períodos (razón de medio período):

{displaystyle {frac {1}{4}}ln {bigl (}{frac {16}{x^{2}}}{bigr)}-{frac {pi ,K'(x)}{4,K(x)}}=sum _{n=1}^{infty }{frac {{text{Kn}}(n)}{2^{4n-1}n}},x^{2n}}

Secuencia entera de Schellbach Schwarz

El matemático Karl Heinrich Schellbach descubrió la secuencia de números enteros que aparece en la serie de MacLaurin de la función Elliptic Nome. Este científico construyó detalladamente esta secuencia A002103 en su obra Die Lehre von den elliptischen Integralen und den Thetafunktionen. Especialmente en la página 60 de esta obra se anota una ruta de síntesis de esta secuencia en su obra. También el matemático alemán de Silesia Hermann Amandus Schwarz escribió en su obra Formeln und Lehrsätze zum Gebrauche der elliptischen Funktionen en el capítulo Berechnung der Grösse k en las páginas 54 a 56 que la secuencia de números enteros abajo. Esta secuencia numérica de Schellbach Schwarz Sc(n) (OEIS: A002103) también fue analizada por los matemáticos Karl Theodor Wilhelm Weierstrass y Louis Melville Milne-Thomson en el siglo XX. El matemático Adolf Kneser determinó un método de síntesis para esta secuencia basándose en el siguiente patrón:

{displaystyle {text{Sc}}(n+1)={frac {2}{n}}sum _{m=1}^{n}{text{Sc}}(m){text{Kn}}(n+1-m)}

La secuencia de Schellbach Schwarz Sc(n) se ingresa en la enciclopedia en línea de secuencias numéricas con el número A002103 y la secuencia de Kneser Kn(n) se ingresa con el número A227503. Adolf Kneser investigó esta secuencia entera en su ensayo Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen y demostró que la función generadora de esta secuencia es una función elíptica. También Robert Fricke analizó esta secuencia de enteros en su ensayo Die elliptischen Funktionen und ihre Anwendungen y describió métodos de cálculo precisos utilizando esta secuencia. La siguiente tabla contiene los números de Kneser y los números de Schellbach Schwarz:

Secuencias construidas Kneser y Schellbach Schwarz
Índice n	Kn(n) (A227503)	Sc(n) (A002103)
1	1	1
2	13	2
3	184	15
4	2701	150
5	40456	1707
6	613720	20910
7	9391936	268616
8	144644749	3567400

A continuación se mostrará como ejemplo cómo se construyen sucesivamente los números de Schellbach Schwarz. Para ello se utilizan los ejemplos con los números Sc(4) = 150, Sc(5) = 1707 y Sc(6) = 20910:

{displaystyle mathrm {Sc} (4)={frac {2}{3}}sum _{m=1}^{3}mathrm {Sc} (m),mathrm {Kn} (4-m)={frac {2}{3}}{bigl [}{color {navy}mathrm {Sc} (1)},{color {cornflowerblue}mathrm {Kn} (3)}+{color {navy}mathrm {Sc} (2)},{color {cornflowerblue}mathrm {Kn} (2)}+{color {navy}mathrm {Sc} (3)},{color {cornflowerblue}mathrm {Kn} (1)}{bigr ]}}

{displaystyle {color {navy}mathrm {Sc} (4)}={frac {2}{3}}{bigl (}{color {navy}1}times {color {cornflowerblue}184}+{color {navy}2}times {color {cornflowerblue}13}+{color {navy}15}times {color {cornflowerblue}1}{bigr)}={color {navy}150}}

{displaystyle mathrm {Sc} (5)={frac {2}{4}}sum _{m=1}^{4}mathrm {Sc} (m),mathrm {Kn} (5-m)={frac {2}{4}}{bigl [}{color {navy}mathrm {Sc} (1)},{color {cornflowerblue}mathrm {Kn} (4)}+{color {navy}mathrm {Sc} (2)},{color {cornflowerblue}mathrm {Kn} (3)}+{color {navy}mathrm {Sc} (3)},{color {cornflowerblue}mathrm {Kn} (2)}+{color {navy}mathrm {Sc} (4)},{color {cornflowerblue}mathrm {Kn} (1)}{bigr ]}}

{displaystyle {color {navy}mathrm {Sc} (5)}={frac {2}{4}}{bigl (}{color {navy}1}times {color {cornflowerblue}2701}+{color {navy}2}times {color {cornflowerblue}184}+{color {navy}15}times {color {cornflowerblue}13}+{color {navy}150}times {color {cornflowerblue}1}{bigr)}={color {navy}1707}}

{displaystyle mathrm {Sc} (6)={frac {2}{5}}sum _{m=1}^{5}mathrm {Sc} (m),mathrm {Kn} (6-m)={frac {2}{5}}{bigl [}{color {navy}mathrm {Sc} (1)},{color {cornflowerblue}mathrm {Kn} (5)}+{color {navy}mathrm {Sc} (2)},{color {cornflowerblue}mathrm {Kn} (4)}+{color {navy}mathrm {Sc} (3)},{color {cornflowerblue}mathrm {Kn} (3)}+{color {navy}mathrm {Sc} (4)},{color {cornflowerblue}mathrm {Kn} (2)}+{color {navy}mathrm {Sc} (5)},{color {cornflowerblue}mathrm {Kn} (1)}{bigr ]}}

{displaystyle {color {navy}mathrm {Sc} (6)}={frac {2}{5}}{bigl (}{color {navy}1}times {color {cornflowerblue}40456}+{color {navy}2}times {color {cornflowerblue}2701}+{color {navy}15}times {color {cornflowerblue}184}+{color {navy}150}times {color {cornflowerblue}13}+{color {navy}1707}times {color {cornflowerblue}1}{bigr)}={color {navy}20910}}

Y esta secuencia crea la serie MacLaurin del nomo elíptico exactamente de esta manera mencionada anteriormente:

{displaystyle q(x)=sum _{n=1}^{infty }{frac {{text{Sc}}(n)}{2^{4n-3}}}{biggl (}{frac {1-{sqrt[{4}]{1-x^{2}}}}{1+{sqrt[{4}]{1-x^{2}}}}}{biggr)}^{4n-3}=x^{2}{biggl {}{frac {1}{2}}+{biggl [}sum _{n=1}^{infty }{frac {{text{Sc}}(n+1)}{2^{4n+1}}}x^{2n}{biggr ]}{biggr }}^{4}}

Definición en términos de funciones theta de Neville

Las funciones elípticas de Jacobi se pueden definir de forma muy sencilla utilizando las funciones theta de Neville:

{displaystyle operatorname {pq} (u,m)={frac {theta _{operatorname {p} }(u,m)}{theta _{operatorname {q} }(u,m)}}}

Las simplificaciones de productos complicados de las funciones elípticas de Jacobi a menudo se facilitan utilizando estas identidades.

Transformaciones de Jacobi

Las transformaciones imaginarias de Jacobi

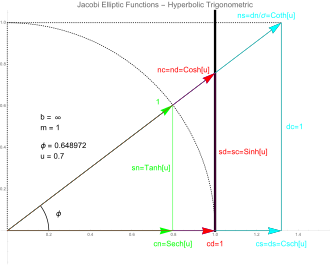
Parcela de la curva degenerada Jacobi (x²+*Sí.*²/b²= 1, b= ∞) y las doce funciones elípticas Jacobi pq(u,1) para un valor particular del ánguloφ. La curva sólida es la elipse degeneradax²= 1) con m= 1 y u=F()φ,1) donde F(·,middot') es la integral elíptica del primer tipo. La curva punteada es el círculo de la unidad. Ya que estas son las funciones de Jacobi m= 0 (funciones trigonométricas circulares) pero con argumentos imaginarios, corresponden a las seis funciones trigonométricas hiperbólicas.

Las transformaciones imaginarias de Jacobi relacionan varias funciones de la variable imaginaria i u o, de manera equivalente, relaciones entre varios valores del parámetro m. En cuanto a las funciones principales:

{displaystyle operatorname {cn} (u,m)=operatorname {nc} (i,u,1!-!m)}

{displaystyle operatorname {sn} (u,m)=-ioperatorname {sc} (i,u,1!-!m)}

{displaystyle operatorname {dn} (u,m)=operatorname {dc} (i,u,1!-!m)}

Utilizando la regla de multiplicación, todas las demás funciones pueden expresarse en términos de los tres anteriores. Las transformaciones pueden ser escritas generalmente como ${displaystyle operatorname {pq} (u,m)=gamma _{operatorname {pq} }operatorname {pq} '(i,u,1!-!m)}$ . La tabla siguiente da ${displaystyle gamma _{operatorname {pq} }operatorname {pq} '(i,u,1!-!m)}$ para el pq(u,m). (Los argumentos ${displaystyle (i,u,1!-!m)}$ son suprimidos)

Jacobi Transformaciones imaginarias ${displaystyle gamma _{operatorname {pq} }operatorname {pq} '(i,u,1!-!m)}$
		q
		c	s	n	d
p
	c	1	I ns	nc	nd
	s	−i sn	1	−i sc	−i sd
	n	cn	i c	1	cd
	d	♪	i ds	dc	1

Dado que las funciones trigonométricas hiperbólicas son proporcionales a las funciones trigonométricas circulares con argumentos imaginarios, se deduce que las funciones de Jacobi producirán las funciones hiperbólicas para m=1. En la figura, la curva de Jacobi ha degenerado en dos líneas verticales en x = 1 y x = −1.

Las transformaciones reales de Jacobi

Las transformaciones reales de Jacobi producen expresiones para las funciones elípticas en términos de valores alternativos de m. Las transformaciones pueden ser escritas generalmente como ${displaystyle operatorname {pq} (u,m)=gamma _{operatorname {pq} }operatorname {pq} '(k,u,1/m)}$ . La tabla siguiente da ${displaystyle gamma _{operatorname {pq} }operatorname {pq} '(k,u,1/m)}$ para el pq(u,m). (Los argumentos ${displaystyle (k,u,1/m)}$ son suprimidos)

Transformaciones reales de Jacobi ${displaystyle gamma _{operatorname {pq} }operatorname {pq} '(k,u,1/m)}$
		q
		c	s	n	d
p
	c	$1$	${displaystyle koperatorname {ds} }$	${displaystyle operatorname {dn} }$	${displaystyle operatorname {dc} }$
	s	${displaystyle {frac {1}{k}}operatorname {sd} }$	$1$	${displaystyle {frac {1}{k}}operatorname {sn} }$	${displaystyle {frac {1}{k}}operatorname {sc} }$
	n	${displaystyle operatorname {nd} }$	${displaystyle koperatorname {ns} }$	$1$	${displaystyle operatorname {nc} }$
	d	${displaystyle operatorname {cd} }$	${displaystyle koperatorname {cs} }$	${displaystyle operatorname {cn} }$	$1$

Otras transformaciones de Jacobi

Las transformaciones reales e imaginarias de Jacobi se pueden combinar de varias maneras para producir tres transformaciones más simples. . Las transformaciones real e imaginaria son dos transformaciones en un grupo (D3 o grupo anarmónico) de seis transformaciones. Si

{displaystyle mu _{R}(m)=1/m}

es la transformación para el parámetro m en la transformación real, y

{displaystyle mu _{I}(m)=1-m=m'}

es la transformación de m en la transformación imaginaria, entonces las otras transformaciones pueden construirse mediante la aplicación sucesiva de estas dos transformaciones básicas, dando solo tres posibilidades más:

{displaystyle {begin{aligned}mu _{IR}(m)&=&mu _{I}(mu _{R}(m))&=&-m'/m\mu _{RI}(m)&=&mu _{R}(mu _{I}(m))&=&1/m'\mu _{RIR}(m)&=&mu _{R}(mu _{I}(mu _{R}(m)))&=&-m/m'end{aligned}}}

Estas cinco transformaciones, junto con la transformación de identidad (μ_U(m) = m) produce el grupo de seis elementos. Con respecto a las funciones elípticas de Jacobi, la transformación general se puede expresar utilizando sólo tres funciones:

{displaystyle operatorname {cs} (u,m)=gamma _{i}operatorname {cs'} (gamma _{i}u,mu _{i}(m))}

{displaystyle operatorname {ns} (u,m)=gamma _{i}operatorname {ns'} (gamma _{i}u,mu _{i}(m))}

{displaystyle operatorname {ds} (u,m)=gamma _{i}operatorname {ds'} (gamma _{i}u,mu _{i}(m))}

donde i = U, I, IR, R, RI o RIR, identificando la transformación, γ_i es un factor de multiplicación común a estas tres funciones, y el primo indica la función transformada. Las otras nueve funciones transformadas se pueden construir a partir de las tres anteriores. La razón por la que se eligieron las funciones cs, ns, ds para representar la transformación es que las otras funciones serán razones de estas tres (excepto sus inversas) y los factores de multiplicación se cancelarán.

La tabla siguiente enumera los factores de multiplicación para las tres funciones de ps, la transformada m's, y los nombres de función transformados para cada una de las seis transformaciones. (Como siempre, k²=m, 1 −k²=k₁²=m′ y los argumentos ( ${displaystyle gamma _{i}u,mu _{i}(m)}$ ) son suprimidos)

Parámetros para las seis transformaciones
Transformación i	$gamma _{i}$	${displaystyle mu _{i}(m)}$	c '	ns '	ds '
U	1	m	c	ns	ds
I	i	m '	ns	c	ds
IR	i k	−m	ds	c	ns
R	k	1/m	ds	ns	c
RI	i k₁	1/m '	ns	ds	c
RIR	k₁	−m/m '	c	ds	ns

Por ejemplo, podemos construir la siguiente tabla para la transformación RIR. La transformación generalmente está escrita ${displaystyle operatorname {pq} (u,m)=gamma _{operatorname {pq} },operatorname {pq'} (k',u,-m/m')}$ (Los argumentos ${displaystyle (k',u,-m/m')}$ son suprimidos)

La transformación RIR ${displaystyle gamma _{operatorname {pq} },operatorname {pq'} (k',u,-m/m')}$
		q
		c	s	n	d
p
	c	1	k' cs	cd	cn
	s	${frac {1}{k'}}$ sc	1	${frac {1}{k'}}$ sd	${displaystyle {frac {1}{k'}}}$ sn
	n	dc	$k'$ ds	1	♪
	d	nc	$k'$ ns	nd	1

El valor de las transformaciones de Jacobi es que cualquier conjunto de funciones elípticas de Jacobi con cualquier parámetro de valor complejo m se puede convertir en otro conjunto para el cual 0 ≤ m ≤ 1 y, para valores reales de u, los valores de la función serán reales.

La hipérbola de Jacobi

Al presentar números complejos, nuestra elipse tiene una hipérbola asociada:

{displaystyle x^{2}-{frac {y^{2}}{b^{2}}}=1}

Did you mean:

from applying Jacob 's imaginary transformation to the elliptic functions in the above equation for x and y.

{displaystyle x={frac {1}{operatorname {dn} (u,1-m)}},quad y={frac {operatorname {sn} (u,1-m)}{operatorname {dn} (u,1-m)}}}

Sigue que podemos poner ${displaystyle x=operatorname {dn} (u,1-m),y=operatorname {sn} (u,1-m)}$ . Así que nuestra elipse tiene un doble elipse con m reemplazado por 1-m. Esto conduce al complejo torus mencionado en la Introducción. Por lo general, m puede ser un número complejo, pero cuando m es real y m observado0, la curva es un elipse con eje principal en la dirección x. A m=0 la curva es un círculo, y para 0 segmentó1, la curva es un elipse con eje principal en la dirección y. At m= 1, la curva degenera en dos líneas verticales x= ±1. mLa curva es una hiperbola. Cuando m es complejo pero no real, x o Sí. o ambos son complejos y la curva no se puede describir en un real x-Sí. diagrama.

Funciones menores

Invertir el orden de las dos letras del nombre de la función da como resultado los recíprocos de las tres funciones anteriores:

{displaystyle operatorname {ns} (u)={frac {1}{operatorname {sn} (u)}},qquad operatorname {nc} (u)={frac {1}{operatorname {cn} (u)}},qquad operatorname {nd} (u)={frac {1}{operatorname {dn} (u)}}.}

De manera similar, las razones de las tres funciones primarias corresponden a la primera letra del numerador seguida de la primera letra del denominador:

{displaystyle {begin{aligned}operatorname {sc} (u)={frac {operatorname {sn} (u)}{operatorname {cn} (u)}},qquad operatorname {sd} (u)={frac {operatorname {sn} (u)}{operatorname {dn} (u)}},qquad operatorname {dc} (u)={frac {operatorname {dn} (u)}{operatorname {cn} (u)}},qquad operatorname {ds} (u)={frac {operatorname {dn} (u)}{operatorname {sn} (u)}},qquad operatorname {cs} (u)={frac {operatorname {cn} (u)}{operatorname {sn} (u)}},qquad operatorname {cd} (u)={frac {operatorname {cn} (u)}{operatorname {dn} (u)}}.end{aligned}}}

De manera más compacta, tenemos

{displaystyle operatorname {pq} (u)={frac {operatorname {pn} (u)}{operatorname {qn} (u)}}}

donde p y q son cualquiera de las letras s, c, d.

Periodicidad, polos y residuos

Parcelas de la fase para las doce funciones Elípticas Jacobi pq(u,m) como un argumento complejo de función u, con polos y ceros indicados. Las parcelas están sobre un ciclo completo en las direcciones reales e imaginarias con la porción coloreada indicando fase según la rueda de color en la derecha inferior (que reemplaza la función trivial dd). Las regiones con valor absoluto inferior a 1/3 son de color negro, aproximadamente indicando la ubicación de un cero, mientras que las regiones con valor absoluto superior a 3 son de color blanco, aproximadamente indicando la posición de un polo. Todas las parcelas usan m= 2/3 con K=K()m), K′ =K(1 −m), K(·) siendo la integral elíptica completa del primer tipo. Arrows en los polos apuntan hacia la fase cero. Las flechas derecha e izquierda implican residuos reales positivos y negativos respectivamente. Las flechas arriba y abajo implican residuos imaginarios positivos y negativos respectivamente.

En el plano complejo del argumento u, las funciones elípticas de Jacobi forman un patrón repetido de polos (y ceros). Todos los residuos de los polos tienen el mismo valor absoluto y sólo difieren en el signo. Cada función pq(u,m) tiene una "función inversa" (en sentido multiplicativo) qp(u,m) en el que se intercambian las posiciones de los polos y ceros. Los períodos de repetición son generalmente diferentes en las direcciones real e imaginaria, de ahí el uso del término "doblemente periódico" para describirlos.

La amplitud de Jacobi y la función épsilon de Jacobi son cuasi periódicas:

{displaystyle operatorname {am} (u+2K,m)=operatorname {am} (u,m)+pi}

{displaystyle {mathcal {E}}(u+2K,m)={mathcal {E}}(u,m)+2E}

Donde $E(m)$ es la integral elíptica completa del segundo tipo con parámetro $m$ .

También

{displaystyle operatorname {zn} (u+2iK',m)=operatorname {zn} (u,m)-{frac {pi i}{K}}}

La doble periodicidad de las funciones elípticas de Jacobi se puede expresar como:

{displaystyle operatorname {pq} (u+2alpha K(m)+2ibeta K(1-m),,,m)=(-1)^{gamma }operatorname {pq} (u,m)}

donde α y β son cualquier par de números enteros. K(·) es la integral elíptica completa de primer tipo, también conocida como cuarto de período. El poder de la unidad negativa (γ) se da en la siguiente tabla:

$gamma$
		q
		c	s	n	d
p
	c	0	β	α + β	α
	s	β	0	α	α + β
	n	α + β	α	0	β
	d	α	α + β	β	0

Cuando el factor (−1)^γ es igual a −1, la ecuación expresa cuasi-periodicidad. Cuando es igual a la unidad, expresa periodicidad completa. Se puede ver, por ejemplo, que para las entradas que contienen sólo α cuando α es par, la periodicidad completa se expresa mediante la ecuación anterior, y la función tiene períodos completos de 4K(m ) y 2iK(1 − m). Del mismo modo, las funciones con entradas que contienen sólo β tienen períodos completos de 2K(m) y 4iK(1 − m), mientras que aquellas con α + β tienen períodos completos de 4K(m) y 4iK(1 − m).

En el diagrama de la derecha, que traza una unidad repetida para cada función, indicando la fase junto con la ubicación de los polos y los ceros, se pueden observar varias regularidades: La inversa de cada función es opuesta a la diagonal y tiene Celda unitaria del mismo tamaño, con polos y ceros intercambiados. La disposición de polos y ceros en el rectángulo auxiliar formado por (0,0), (K,0), (0,K′) y (K,K′) están de acuerdo con la descripción de la ubicación del polo y del cero descrita en la introducción anterior. Además, el tamaño de los óvalos blancos que indican los polos es una medida aproximada del valor absoluto del residuo de ese polo. Los residuos de los polos más cercanos al origen en la figura (es decir, en el rectángulo auxiliar) se enumeran en la siguiente tabla:

Residuos de Jacobi Funciones Elípticas
		q
		c	s	n	d
p
	c		1	${displaystyle -{frac {i}{k}}}$	${displaystyle -{frac {1}{k}}}$
	s	${displaystyle -{frac {1}{k'}}}$		${frac {1}{k}}$	${displaystyle -{frac {i}{k,k'}}}$
	n	${displaystyle -{frac {1}{k'}}}$	1		${displaystyle -{frac {i}{k'}}}$
	d	-1	1	$-i$

Cuando corresponda, los polos desplazados arriba 2K o desplazados hacia la derecha 2K′ tienen el mismo valor pero con signos invertidos, mientras que los diagonalmente opuestos tienen el mismo valor. mismo valor. Tenga en cuenta que los polos y ceros de los bordes izquierdo e inferior se consideran parte de la celda unitaria, mientras que los de los bordes superior y derecho no lo son.

Valores especiales

Valores lemniscaticos

Los valores junto con el módulo ${displaystyle k={tfrac {1}{2}}{sqrt {2}}=lambda ^{*}(1)}$ se llaman valores lemniscaticos:

Valores para los tercios de la integral K:

{displaystyle operatorname {sn} {bigl [}{tfrac {1}{3}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}({sqrt[{4}]{12}}-{sqrt {3}}+1)}

{displaystyle operatorname {cn} {bigl [}{tfrac {2}{3}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}({sqrt {3}}-{sqrt[{4}]{12}}+1)}

{displaystyle operatorname {cn} {bigl [}{tfrac {1}{3}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={sqrt[{4}]{2{sqrt {3}}-3}}}

{displaystyle operatorname {sn} {bigl [}{tfrac {2}{3}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}({sqrt[{4}]{27}}+{sqrt[{4}]{3}}-{sqrt {2}}){sqrt[{4}]{2{sqrt {3}}-3}}}

Valores para las quintas de la integral K:

{displaystyle operatorname {sn} {bigl [}{tfrac {1}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{bigl [}tan({tfrac {1}{5}}pi)+1-{sqrt {2tan({tfrac {3}{20}}pi)}}{bigr ]}}

{displaystyle operatorname {sn} {bigl [}{tfrac {3}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{bigl [}tan({tfrac {1}{5}}pi)-1+{sqrt {2cot({tfrac {3}{20}}pi)}}{bigr ]}}

{displaystyle operatorname {cn} {bigl [}{tfrac {2}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{bigl [}cot({tfrac {1}{10}}pi)-1-{sqrt {2tan({tfrac {1}{20}}pi)}}{bigr ]}}

{displaystyle operatorname {cn} {bigl [}{tfrac {4}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{bigl [}cot({tfrac {1}{10}}pi)+1-{sqrt {2cot({tfrac {1}{20}}pi)}}{bigr ]}}

Para los correspondientes opuestos pitagóricos estas fórmulas son válidas:

{displaystyle operatorname {cn} {bigl [}{tfrac {1}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}=2{sqrt[{4}]{{sqrt {5}}-2}},{sqrt {sin({tfrac {3}{20}}pi)cos({tfrac {1}{20}}pi)}}}

{displaystyle operatorname {cn} {bigl [}{tfrac {3}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}=2{sqrt[{4}]{{sqrt {5}}-2}},{sqrt {sin({tfrac {1}{20}}pi)cos({tfrac {3}{20}}pi)}}}

{displaystyle operatorname {sn} {bigl [}{tfrac {2}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{sqrt[{4}]{2tan({tfrac {1}{20}}pi)}},({sqrt {cot({tfrac {1}{10}}pi)+1}}-{sqrt {cot({tfrac {1}{10}}pi)-3}})}

{displaystyle operatorname {sn} {bigl [}{tfrac {4}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{sqrt[{4}]{2cot({tfrac {1}{20}}pi)}},({sqrt {cot({tfrac {1}{10}}pi)+3}}-{sqrt {cot({tfrac {1}{10}}pi)-1}})}

Valores para las séptimas de la integral K:

{displaystyle operatorname {cn} [{tfrac {2}{7}}K({tfrac {1}{2}}{sqrt {2}});{tfrac {1}{2}}{sqrt {2}}]=tanh {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}{sqrt {2sin({tfrac {1}{7}}pi)cot({tfrac {3}{28}}pi)}}+sin({tfrac {1}{14}}pi){bigr ]}{bigr }}}

{displaystyle operatorname {cn} [{tfrac {4}{7}}K({tfrac {1}{2}}{sqrt {2}});{tfrac {1}{2}}{sqrt {2}}]=tanh {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}{sqrt {2cos({tfrac {1}{14}}pi)tan({tfrac {5}{28}}pi)}}+sin({tfrac {3}{14}}pi){bigr ]}{bigr }}}

{displaystyle operatorname {cn} [{tfrac {6}{7}}K({tfrac {1}{2}}{sqrt {2}});{tfrac {1}{2}}{sqrt {2}}]=tanh {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}{sqrt {2cos({tfrac {3}{14}}pi)cot({tfrac {1}{28}}pi)}}+cos({tfrac {1}{7}}pi){bigr ]}{bigr }}}

Para los correspondientes opuestos pitagóricos estas fórmulas son válidas:

{displaystyle operatorname {sn} [{tfrac {2}{7}}K({tfrac {1}{2}}{sqrt {2}});{tfrac {1}{2}}{sqrt {2}}]=operatorname {sech} {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}{sqrt {2sin({tfrac {1}{7}}pi)cot({tfrac {3}{28}}pi)}}+sin({tfrac {1}{14}}pi){bigr ]}{bigr }}}

{displaystyle operatorname {sn} [{tfrac {4}{7}}K({tfrac {1}{2}}{sqrt {2}});{tfrac {1}{2}}{sqrt {2}}]=operatorname {sech} {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}{sqrt {2cos({tfrac {1}{14}}pi)tan({tfrac {5}{28}}pi)}}+sin({tfrac {3}{14}}pi){bigr ]}{bigr }}}

{displaystyle operatorname {sn} [{tfrac {6}{7}}K({tfrac {1}{2}}{sqrt {2}});{tfrac {1}{2}}{sqrt {2}}]=operatorname {sech} {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}{sqrt {2cos({tfrac {3}{14}}pi)cot({tfrac {1}{28}}pi)}}+cos({tfrac {1}{7}}pi){bigr ]}{bigr }}}

Identidades importantes:

Ajuste ${displaystyle k={tfrac {1}{2}}{sqrt {2}}}$ lemniscate funciones elípticas ${displaystyle operatorname {sl} }$ y ${displaystyle operatorname {cl} }$ de esta manera:

{displaystyle operatorname {sl} (u)={tfrac {1}{2}}{sqrt {2}},operatorname {sd} ({sqrt {2}},u;{tfrac {1}{2}}{sqrt {2}},)={tfrac {1}{2}}{sqrt {2}},{frac {operatorname {sn} ({sqrt {2}},u;{tfrac {1}{2}}{sqrt {2}},)}{operatorname {dn} ({sqrt {2}},u;{tfrac {1}{2}}{sqrt {2}},)}},quad operatorname {cl} (u)=operatorname {cn} ({sqrt {2}},u;{tfrac {1}{2}}{sqrt {2}},).}

Ajuste ${displaystyle k=i}$ lemniscate funciones elípticas ${displaystyle operatorname {sl} }$ y ${displaystyle operatorname {cl} }$ de la siguiente manera:

{displaystyle operatorname {sl} (u)=operatorname {sn} (u;i),quad operatorname {cl} (u)=operatorname {cd} (u;i)={frac {operatorname {cn} (u;i)}{operatorname {dn} (u;i)}}.}

Did you mean:

Equian Harmonic values

Los valores junto con el módulo ${displaystyle k=sin({tfrac {1}{12}}pi)=lambda ^{*}(3)}$ y ${displaystyle k=cos({tfrac {1}{12}}pi)=lambda ^{*}({tfrac {1}{3}})}$ son llamados valores equianharmónicos o también valores de los Equianharmonic Caso:

{displaystyle operatorname {cn} {{tfrac {2}{5}}K{bigl [}sin({tfrac {1}{12}}pi){bigr ]};sin({tfrac {1}{12}}pi)}=tan {bigl {}arctan {bigl [}{sqrt[{3}]{10}}tan({tfrac {1}{10}}pi)+{tfrac {1}{3}}{sqrt {3}}({sqrt[{3}]{10}}-1){bigr ]}-{tfrac {1}{12}}pi {bigr }}}

{displaystyle operatorname {cn} {{tfrac {4}{5}}K{bigl [}sin({tfrac {1}{12}}pi){bigr ]};sin({tfrac {1}{12}}pi)}=tan {bigl {}arctan {bigl [}{sqrt[{3}]{10}}tan({tfrac {1}{10}}pi)-{tfrac {1}{3}}{sqrt {3}}({sqrt[{3}]{10}}-1){bigr ]}+{tfrac {1}{12}}pi {bigr }}}

{displaystyle operatorname {cn} {{tfrac {2}{5}}K{bigl [}cos({tfrac {1}{12}}pi){bigr ]};cos({tfrac {1}{12}}pi)}=cot {bigl {}arctan {bigl [}{sqrt[{3}]{10}}cot({tfrac {1}{5}}pi)+{tfrac {1}{3}}{sqrt {3}}({sqrt[{3}]{10}}-1){bigr ]}-{tfrac {1}{12}}pi {bigr }}}

{displaystyle operatorname {cn} {{tfrac {4}{5}}K{bigl [}cos({tfrac {1}{12}}pi){bigr ]};cos({tfrac {1}{12}}pi)}=cot {bigl {}arctan {bigl [}{sqrt[{3}]{10}}cot({tfrac {1}{5}}pi)-{tfrac {1}{3}}{sqrt {3}}({sqrt[{3}]{10}}-1){bigr ]}+{tfrac {1}{12}}pi {bigr }}}

¡La flor marca la función de estrella lambda elíptica!

Funciones elementales

Cuando $k=0$ o $k=1$ , las funciones elípticas Jacobi se reducen a funciones no inteligentes:

Función	k = 0	k = 1
${displaystyle operatorname {sn} (u;k)}$	${displaystyle sin u}$	${displaystyle tanh u}$
${displaystyle operatorname {cn} (u;k)}$	${displaystyle cos u}$	${displaystyle operatorname {sech} u}$
${displaystyle operatorname {dn} (u;k)}$	$1$	${displaystyle operatorname {sech} u}$
${displaystyle operatorname {ns} (u;k)}$	${displaystyle csc u}$	${displaystyle coth u}$
${displaystyle operatorname {nc} (u;k)}$	${displaystyle sec u}$	${displaystyle cosh u}$
${displaystyle operatorname {nd} (u;k)}$	$1$	${displaystyle cosh u}$
${displaystyle operatorname {sd} (u;k)}$	${displaystyle sin u}$	${displaystyle sinh u}$
${displaystyle operatorname {cd} (u;k)}$	${displaystyle cos u}$	$1$
${displaystyle operatorname {cs} (u;k)}$	${displaystyle cot u}$	${displaystyle operatorname {csch} u}$
${displaystyle operatorname {ds} (u;k)}$	${displaystyle csc u}$	${displaystyle operatorname {csch} u}$
${displaystyle operatorname {dc} (u;k)}$	${displaystyle sec u}$	$1$
${displaystyle operatorname {sc} (u;k)}$	${displaystyle tan u}$	${displaystyle sinh u}$

Por la amplitud de Jacobi, ${displaystyle operatorname {am} (u;0)=u}$ y ${displaystyle operatorname {am} (u;1)=operatorname {gd} u}$ Donde ${displaystyle operatorname {gd} }$ es la función Gudermanniana.

En general si ninguna de las p, q es d entonces ${displaystyle operatorname {pq} (u;1)=operatorname {pq} (operatorname {gd} (u);0)}$ .

Identidades

Teoremas de la suma

Las funciones satisfacen las dos relaciones cuadradas en dependencia del módulo $k$ en forma Legendre:

{displaystyle operatorname {cn} ^{2}(u;k)+operatorname {sn} ^{2}(u;k)=1,,}

{displaystyle operatorname {dn} ^{2}(u;k)+k^{2}operatorname {sn} ^{2}(u;k)=1.,}

De esto vemos que (cn, sn, dn) parametriza una curva elíptica que es la intersección de las dos cuádricas definidas por las dos ecuaciones anteriores. Ahora podemos definir una ley de grupo para puntos en esta curva mediante las fórmulas de suma para las funciones de Jacobi

{displaystyle {begin{aligned}operatorname {sn} (x+y;k)&={operatorname {sn} (x;k)operatorname {cn} (y;k)operatorname {dn} (y;k)+operatorname {sn} (y;k)operatorname {cn} (x;k)operatorname {dn} (x;k) over {1-k^{2}operatorname {sn} ^{2}(x;k)operatorname {sn} ^{2}(y;k)}},\[8pt]operatorname {cn} (x+y;k)&={operatorname {cn} (x;k)operatorname {cn} (y;k)-operatorname {sn} (x;k)operatorname {sn} (y;k)operatorname {dn} (x;k)operatorname {dn} (y;k) over {1-k^{2}operatorname {sn} ^{2}(x;k)operatorname {sn} ^{2}(y;k)}},\[8pt]operatorname {dn} (x+y;k)&={operatorname {dn} (x;k)operatorname {dn} (y;k)-k^{2}operatorname {sn} (x;k)operatorname {sn} (y;k)operatorname {cn} (x;k)operatorname {cn} (y;k) over {1-k^{2}operatorname {sn} ^{2}(x;k)operatorname {sn} ^{2}(y;k)}}.end{aligned}}}

Tratando únicamente las funciones sn y cd, se pueden establecer el siguiente par de teoremas de suma en los que los dos teoremas son antisimétricos entre sí:

${displaystyle {color {blueviolet}operatorname {sn} }(x+y;k)={frac {{color {blueviolet}operatorname {sn} }(x;k),{color {blue}operatorname {cd} }(y;k)+{color {blue}operatorname {cd} }(x;k),{color {blueviolet}operatorname {sn} }(y;k)}{1+k^{2},{color {blueviolet}operatorname {sn} }(x;k),{color {blue}operatorname {cd} }(x;k),{color {blueviolet}operatorname {sn} }(y;k){color {blue}operatorname {cd} }(y;k)}}}$
${displaystyle {color {blue}operatorname {cd} }(x+y;k)={frac {{color {blue}operatorname {cd} }(x;k),{color {blue}operatorname {cd} }(y;k)-{color {blueviolet}operatorname {sn} }(x;k),{color {blueviolet}operatorname {sn} }(y;k)}{1-k^{2},{color {blueviolet}operatorname {sn} }(x;k),{color {blue}operatorname {cd} }(x;k),{color {blueviolet}operatorname {sn} }(y;k),{color {blue}operatorname {cd} }(y;k)}}}$

Las funciones Jacobi épsilon y zn satisfacen un teorema de cuasi suma:

{displaystyle {begin{aligned}{mathcal {E}}(x+y;k)&={mathcal {E}}(x;k)+{mathcal {E}}(y;k)-k^{2}operatorname {sn} (x;k)operatorname {sn} (y;k)operatorname {sn} (x+y;k),\operatorname {zn} (x+y;k)&=operatorname {zn} (x;k)+operatorname {zn} (y;k)-k^{2}operatorname {sn} (x;k)operatorname {sn} (y;k)operatorname {sn} (x+y;k).end{aligned}}}

Did you mean:

Double angle formula can be easily derived from the above equations by setting x = y. Half angle formula are all of the form:

{displaystyle operatorname {pq} ({tfrac {1}{2}}u;k)^{2}=f_{mathrm {p} }/f_{mathrm {q} }}

donde:

{displaystyle f_{mathrm {c} }=operatorname {cn} (u;k)+operatorname {dn} (u;k)}

{displaystyle f_{mathrm {s} }=1-operatorname {cn} (u;k)}

{displaystyle f_{mathrm {n} }=1+operatorname {dn} (u;k)}

{displaystyle f_{mathrm {d} }=(1+operatorname {dn} (u;k))-m(1-operatorname {cn} (u;k))}

Fórmula del medio ángulo

Estas tres fórmulas describen el teorema de la reducción a la mitad:

{displaystyle operatorname {sn} left({frac {u}{2}};kright)^{2}={frac {1-operatorname {cn} (u;k)}{1+operatorname {dn} (u;k)}}}

{displaystyle operatorname {cn} left({frac {u}{2}};kright)^{2}={frac {operatorname {cn} (u;k)+operatorname {dn} (u;k)}{1+operatorname {dn} (u;k)}}}

{displaystyle operatorname {dn} left({frac {u}{2}};kright)^{2}={frac {1-k^{2}+operatorname {dn} (u;k)+k^{2}operatorname {cn} (u;k)}{1+operatorname {dn} (u;k)}}}

Y el teorema de la media aritmética se describe mediante esta fórmula:

{displaystyle operatorname {sn} {bigl (}{frac {1}{2}},x+{frac {1}{2}},y;,k{bigr)}^{2}={frac {1+operatorname {sn} (x;k)operatorname {sn} (y;k)-operatorname {cn} (x;k)operatorname {cn} (y;k)}{1+k^{2}operatorname {sn} (x;k)operatorname {sn} (y;k)+operatorname {dn} (x;k)operatorname {dn} (y;k)}}}

K fórmulas

Fórmula de media K

{displaystyle operatorname {sn} left[{tfrac {1}{2}}K(k);kright]={frac {sqrt {2}}{{sqrt {1+k}}+{sqrt {1-k}}}}}

{displaystyle operatorname {cn} left[{tfrac {1}{2}}K(k);kright]={frac {{sqrt {2}},{sqrt[{4}]{1-k^{2}}}}{{sqrt {1+k}}+{sqrt {1-k}}}}}

{displaystyle operatorname {dn} left[{tfrac {1}{2}}K(k);kright]={sqrt[{4}]{1-k^{2}}}}

Tercera fórmula K

Además, esta ecuación conduce al valor sn del tercio de K:

{displaystyle k^{2}s^{4}-2k^{2}s^{3}+2s-1=0}

{displaystyle s=operatorname {sn} left[{tfrac {1}{3}}K(k);kright]}

Estas ecuaciones conducen a los otros valores de las funciones de Jacobi:

{displaystyle operatorname {cn} left[{tfrac {2}{3}}K(k);kright]=1-operatorname {sn} left[{tfrac {1}{3}}K(k);kright]}

{displaystyle operatorname {dn} left[{tfrac {2}{3}}K(k);kright]=1/operatorname {sn} left[{tfrac {1}{3}}K(k);kright]-1}

Sobre la base de la ecuación de cuarto grado ahora mencionada, podemos obtener una fórmula simplificada utilizando el algoritmo de solución para el caso general de la ecuación de cuarto grado. Esta fórmula parametrizada se puede generar de esa manera:

{displaystyle operatorname {sn} {biggl langle }{frac {1}{3}}K{bigl {}tan {bigl [}{frac {1}{2}}arctan {bigl (}x^{3}{bigr)}{bigr ]}{bigr }};tan {bigl [}{frac {1}{2}}arctan {bigl (}x^{3}{bigr)}{bigr ]}{biggr rangle }=tanh {bigl [}{frac {1}{2}}ln {bigl (}{sqrt {2{sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{sqrt {x^{2}+1}}{bigr)}{bigr ]}}

Did you mean:

The Pythagorean opposite given that formula successively:

{displaystyle operatorname {cn} {biggl langle }{frac {1}{3}}K{bigl {}tan {bigl [}{frac {1}{2}}arctan {bigl (}x^{3}{bigr)}{bigr ]}{bigr }};tan {bigl [}{frac {1}{2}}arctan {bigl (}x^{3}{bigr)}{bigr ]}{biggr rangle }=operatorname {sech} {bigl [}{frac {1}{2}}ln {bigl (}{sqrt {2{sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{sqrt {x^{2}+1}}{bigr)}{bigr ]}}

Estas dos fórmulas mencionadas son válidas para todos los valores reales de x, el criterio ${displaystyle xin mathbb {R} }$ se cumple en ambas ecuaciones.

Para obtener x, tomamos la tangente del doble del arcotangente del módulo y luego sacamos la raíz cúbica para que aparezca x.

Did you mean:

And then we insert the generated value x into the right side of the balance of the shown parameterized equations.

En relación con este algoritmo de cálculo, a continuación se dan tres ejemplos:

Primer ejemplo: ${displaystyle {frac {1}{2}}{sqrt {2}}=tan {bigl [}{frac {1}{2}}arctan {bigl (}x^{3}{bigr)}{bigr ]}(x={sqrt {2}},)}$ Si insertamos el valor ${displaystyle x={sqrt {2}},}$ en la fracción mostrada arriba, obtenemos este resultado: ${displaystyle operatorname {sn} {bigl [}{frac {1}{3}}K{bigl (}{frac {1}{2}}{sqrt {2}},{bigr)};{frac {1}{2}}{sqrt {2}},{bigr ]}=tanh {bigl [}{frac {1}{2}}ln {bigl (}{sqrt[{4}]{12}}+{sqrt {3}}{bigr)}{bigr ]}={frac {1}{2}}({sqrt[{4}]{12}}-{sqrt {3}}+1)}$ ${displaystyle operatorname {cn} {bigl [}{frac {1}{3}}K{bigl (}{frac {1}{2}}{sqrt {2}},{bigr)};{frac {1}{2}}{sqrt {2}},{bigr ]}=operatorname {sech} {bigl [}{frac {1}{2}}ln {bigl (}{sqrt[{4}]{12}}+{sqrt {3}}{bigr)}{bigr ]}={sqrt[{4}]{2{sqrt {3}}-3}}}$

Segundo ejemplo: ${displaystyle {frac {1}{2}}=tan {bigl [}{frac {1}{2}}arctan {bigl (}x^{3}{bigr)}{bigr ]}(x={sqrt[{3}]{4/3}},)}$ Si insertamos el valor ${displaystyle x={sqrt[{3}]{4/3}},}$ en la fracción mostrada arriba, obtenemos este resultado: ${displaystyle operatorname {sn} {bigl [}{frac {1}{3}}K{bigl (}{frac {1}{2}}{bigr)};{frac {1}{2}}{bigr ]}=tanh {bigl [}{frac {1}{2}}ln {bigl (}{sqrt {2{sqrt {({tfrac {4}{3}})^{4/3}-({tfrac {4}{3}})^{2/3}+1}}-({tfrac {4}{3}})^{2/3}+2}}+{sqrt {({tfrac {4}{3}})^{2/3}+1}}{bigr)}{bigr ]}}$ ${displaystyle operatorname {cn} {bigl [}{frac {1}{3}}K{bigl (}{frac {1}{2}}{bigr)};{frac {1}{2}}{bigr ]}=operatorname {sech} {bigl [}{frac {1}{2}}ln {bigl (}{sqrt {2{sqrt {({tfrac {4}{3}})^{4/3}-({tfrac {4}{3}})^{2/3}+1}}-({tfrac {4}{3}})^{2/3}+2}}+{sqrt {({tfrac {4}{3}})^{2/3}+1}}{bigr)}{bigr ]}}$

Tercer ejemplo: ${displaystyle {frac {1}{4}}=tan {bigl [}{frac {1}{2}}arctan {bigl (}x^{3}{bigr)}{bigr ]}(x={sqrt[{3}]{8/15}},)}$ Si insertamos el valor ${displaystyle x={sqrt[{3}]{8/15}},}$ en la fracción mostrada arriba, obtenemos este resultado: ${displaystyle operatorname {sn} {bigl [}{frac {1}{3}}K{bigl (}{frac {1}{4}}{bigr)};{frac {1}{4}}{bigr ]}=tanh {bigl [}{frac {1}{2}}ln {bigl (}{sqrt {2{sqrt {({tfrac {8}{15}})^{4/3}-({tfrac {8}{15}})^{2/3}+1}}-({tfrac {8}{15}})^{2/3}+2}}+{sqrt {({tfrac {8}{15}})^{2/3}+1}}{bigr)}{bigr ]}}$ ${displaystyle operatorname {cn} {bigl [}{frac {1}{3}}K{bigl (}{frac {1}{4}}{bigr)};{frac {1}{4}}{bigr ]}=operatorname {sech} {bigl [}{frac {1}{2}}ln {bigl (}{sqrt {2{sqrt {({tfrac {8}{15}})^{4/3}-({tfrac {8}{15}})^{2/3}+1}}-({tfrac {8}{15}})^{2/3}+2}}+{sqrt {({tfrac {8}{15}})^{2/3}+1}}{bigr)}{bigr ]}}$

Fórmula quinta K

La siguiente ecuación tiene la siguiente solución:

{displaystyle 4k^{2}t^{6}+8k^{2}t^{5}+2(1-k^{2})^{2}t-(1-k^{2})^{2}=0}

{displaystyle t={frac {1}{2}}-{frac {1}{2}}k^{2}operatorname {sn} left[{tfrac {2}{5}}K(k);kright]^{2}operatorname {sn} left[{tfrac {4}{5}}K(k);kright]^{2}={frac {operatorname {sn} left[{frac {4}{5}}K(k);kright]^{2}-operatorname {sn} left[{frac {2}{5}}K(k);kright]^{2}}{2operatorname {sn} left[{frac {2}{5}}K(k);kright]operatorname {sn} left[{frac {4}{5}}K(k);kright]}}}

Para obtener los valores sn, colocamos la solución x en las siguientes expresiones:

{displaystyle operatorname {sn} {bigl [}{tfrac {2}{5}}K(k);k{bigr ]}=(1+k^{2})^{-1/2}{sqrt {2(1-t-t^{2})(t^{2}+1-t{sqrt {t^{2}+1}})}}}

{displaystyle operatorname {sn} {bigl [}{tfrac {4}{5}}K(k);k{bigr ]}=(1+k^{2})^{-1/2}{sqrt {2(1-t-t^{2})(t^{2}+1+t{sqrt {t^{2}+1}})}}}

La solución t entre cero y medio es esta solución que debe usarse para estas expresiones.

En relación con el algoritmo de cálculo ahora mencionado, a continuación se proporciona un ejemplo importante:

Esta ecuación de sexto grado se da: ${displaystyle 4k^{2}t^{6}+8k^{2}t^{5}+2(1-k^{2})^{2}t-(1-k^{2})^{2}=0}$ El valor ${displaystyle k={tfrac {1}{2}}{sqrt {2}}}$ será introducido en este ejemplo. Al introducir este valor de módulo y multiplicar toda la ecuación con el factor 4 obtenemos esa ecuación: ${displaystyle 8t^{6}+16t^{5}+2t-1=0}$ Esta es la solución de esa ecuación para t que se encuentra entre cero y medio: ${displaystyle t={tfrac {1}{4}}({sqrt {5}}+1)({sqrt[{4}]{5}}-1)}$ Esta solución t y el módulo correspondiente k se insertarán en las fórmulas para los valores de amplitud sine: ${displaystyle operatorname {sn} {bigl [}{tfrac {2}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}=(1+k^{2})^{-1/2}{sqrt {2(1-t-t^{2})(t^{2}+1-t{sqrt {t^{2}+1}})}},{bigl [}k={tfrac {1}{2}}{sqrt {2}},cap ,t={tfrac {1}{4}}({sqrt {5}}+1)({sqrt[{4}]{5}}-1){bigr ]}}$ ${displaystyle operatorname {sn} {bigl [}{tfrac {4}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}=(1+k^{2})^{-1/2}{sqrt {2(1-t-t^{2})(t^{2}+1+t{sqrt {t^{2}+1}})}},{bigl [}k={tfrac {1}{2}}{sqrt {2}},cap ,t={tfrac {1}{4}}({sqrt {5}}+1)({sqrt[{4}]{5}}-1){bigr ]}}$ Al hacer esto, aparecen los siguientes resultados, que ya se mencionan en la sección de los valores especiales: ${displaystyle operatorname {sn} {bigl [}{tfrac {2}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{sqrt[{4}]{2tan({tfrac {1}{20}}pi)}},({sqrt {cot({tfrac {1}{10}}pi)+1}}-{sqrt {cot({tfrac {1}{10}}pi)-3}})}$ ${displaystyle operatorname {sn} {bigl [}{tfrac {4}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}={tfrac {1}{2}}{sqrt[{4}]{2cot({tfrac {1}{20}}pi)}},({sqrt {cot({tfrac {1}{10}}pi)+3}}-{sqrt {cot({tfrac {1}{10}}pi)-1}})}$ Mediante el uso de las funciones hiperbólicas, estas expresiones equivalentes pueden producirse: ${displaystyle operatorname {sn} {bigl [}{tfrac {2}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}=operatorname {sech} {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}cot {bigl (}{tfrac {1}{10}}pi {bigr)}-{tfrac {1}{2}}{bigr ]}{bigr }}}$ ${displaystyle operatorname {sn} {bigl [}{tfrac {4}{5}}K({tfrac {1}{2}}{sqrt {2}},);{tfrac {1}{2}}{sqrt {2}},{bigr ]}=operatorname {sech} {bigl {}{tfrac {1}{2}}operatorname {arcoth} {bigl [}{tfrac {1}{2}}cot {bigl (}{tfrac {1}{10}}pi {bigr)}+{tfrac {1}{2}}{bigr ]}{bigr }}}$

Según el teorema de Abel Ruffini, es completamente imposible establecer expresiones elementales para los valores de amplitud seno de las quintas de la integral elíptica completa de primer tipo para el caso regular del módulo elíptico.

Relaciones entre cuadrados de las funciones

Las relaciones entre cuadrados de las funciones se pueden derivar de dos relaciones básicas (Argumentos (u,m) suprimidos):

{displaystyle operatorname {cn} ^{2}+operatorname {sn} ^{2}=1}

{displaystyle operatorname {cn} ^{2}+m'operatorname {sn} ^{2}=operatorname {dn} ^{2}}

m + m 'nq

{displaystyle operatorname {cq} ^{2}+operatorname {sq} ^{2}=operatorname {nq} ^{2}}

{displaystyle operatorname {cq} ^{2}{}+m'operatorname {sq} ^{2}=operatorname {dq} ^{2}}

Con q=d, estos corresponden trigonométricamente a las ecuaciones para el círculo de unidad ( $x^2+y^2=r^2$ ) y la unidad elipse ( ${displaystyle x^{2}{}+m'y^{2}=1}$ Con x=cd, Sí.=sd y r=nd. Utilizando la regla de multiplicación, otras relaciones pueden derivarse. Por ejemplo:

{displaystyle -operatorname {dn} ^{2}{}+m'=-moperatorname {cn} ^{2}=moperatorname {sn} ^{2}-m}

{displaystyle -m'operatorname {nd} ^{2}{}+m'=-mm'operatorname {sd} ^{2}=moperatorname {cd} ^{2}-m}

{displaystyle m'operatorname {sc} ^{2}{}+m'=m'operatorname {nc} ^{2}=operatorname {dc} ^{2}-m}

{displaystyle operatorname {cs} ^{2}{}+m'=operatorname {ds} ^{2}=operatorname {ns} ^{2}-m}

Representaciones de los valores de las funciones mediante funciones Theta

Se dan las definiciones de producto de las funciones Jacobi Theta Nullwert tal como las establecieron los matemáticos Edmund Taylor Whittaker y George Neville Watson:

{displaystyle vartheta _{00}(w)=prod _{n=1}^{infty }(1-w^{2n})(1+w^{2n-1})^{2}}

{displaystyle vartheta _{01}(w)=prod _{n=1}^{infty }(1-w^{2n})(1-w^{2n-1})^{2}}

Identidades de terceros de la integral $K$ :

Con las llamadas funciones theta de valor cero del sustantivo elíptico del módulo, se pueden representar muchos valores de funciones jacobianas:

{displaystyle operatorname {sc} [{tfrac {2}{3}}K(k);k]={frac {{sqrt {3}},vartheta _{01}[q(k)^{6}]}{{sqrt {1-k^{2}}},vartheta _{01}[q(k)^{2}]}}}

{displaystyle operatorname {sn} [{tfrac {1}{3}}K(k);k]={frac {2,vartheta _{00}[q(k)]^{2}}{3,vartheta _{00}[q(k)^{3}]^{2}+vartheta _{00}[q(k)]^{2}}}={frac {3,vartheta _{01}[q(k)^{3}]^{2}-vartheta _{01}[q(k)]^{2}}{3,vartheta _{01}[q(k)^{3}]^{2}+vartheta _{01}[q(k)]^{2}}}}

{displaystyle operatorname {cn} [{tfrac {2}{3}}K(k);k]={frac {3,vartheta _{00}[q(k)^{3}]^{2}-vartheta _{00}[q(k)]^{2}}{3,vartheta _{00}[q(k)^{3}]^{2}+vartheta _{00}[q(k)]^{2}}}={frac {2,vartheta _{01}[q(k)]^{2}}{3,vartheta _{01}[q(k)^{3}]^{2}+vartheta _{01}[q(k)]^{2}}}}

Identidades de las quintas partes de la $K$ :

{displaystyle operatorname {sn} [{tfrac {1}{5}}K(k);k]={biggl {}{frac {{sqrt {5}},vartheta _{01}[q(k)^{5}]}{vartheta _{01}[q(k)]}}-1{biggr }}{biggl {}{frac {5,vartheta _{01}[q(k)^{10}]^{2}}{vartheta _{01}[q(k)^{2}]^{2}}}-1{biggr }}^{-1}}

{displaystyle operatorname {sn} [{tfrac {3}{5}}K(k);k]={biggl {}{frac {{sqrt {5}},vartheta _{01}[q(k)^{5}]}{vartheta _{01}[q(k)]}}+1{biggr }}{biggl {}{frac {5,vartheta _{01}[q(k)^{10}]^{2}}{vartheta _{01}[q(k)^{2}]^{2}}}-1{biggr }}^{-1}}

{displaystyle operatorname {cn} [{tfrac {2}{5}}K(k);k]={biggl {}{frac {{sqrt {5}},vartheta _{00}[q(k)^{5}]}{vartheta _{00}[q(k)]}}+1{biggr }}{biggl {}{frac {5,vartheta _{01}[q(k)^{10}]^{2}}{vartheta _{01}[q(k)^{2}]^{2}}}-1{biggr }}^{-1}}

{displaystyle operatorname {cn} [{tfrac {4}{5}}K(k);k]={biggl {}{frac {{sqrt {5}},vartheta _{00}[q(k)^{5}]}{vartheta _{00}[q(k)]}}-1{biggr }}{biggl {}{frac {5,vartheta _{01}[q(k)^{10}]^{2}}{vartheta _{01}[q(k)^{2}]^{2}}}-1{biggr }}^{-1}}

Las combinaciones elementales de funciones theta de valor cero y el nomo elíptico no son suficientes para la representación de los valores de la función jacobiana de las entradas del paréntesis izquierdo más allá de las integrales K racionalmente rotas. Esto requiere las funciones theta distintas de cero del patrón descrito anteriormente.

Funciones elípticas de Jacobi como soluciones de ecuaciones diferenciales ordinarias no lineales

Las derivadas de las tres funciones elípticas básicas de Jacobi son:

{displaystyle {frac {mathrm {d} }{mathrm {d} z}}operatorname {sn} (z)=operatorname {cn} (z)operatorname {dn} (z),}

{displaystyle {frac {mathrm {d} }{mathrm {d} z}}operatorname {cn} (z)=-operatorname {sn} (z)operatorname {dn} (z),}

{displaystyle {frac {mathrm {d} }{mathrm {d} z}}operatorname {dn} (z)=-moperatorname {sn} (z)operatorname {cn} (z).}

Estos se pueden utilizar para derivar las derivadas de todas las demás funciones como se muestra en la siguiente tabla (argumentos (u,m) suprimidos):

Derivativos ${displaystyle {frac {mathrm {d} }{mathrm {d} u}}operatorname {pq} (u,m)}$
		q
		c	s	n	d
p
	c	0	−ds ns	−dn sn	−m-nd sd
	s	dc nc	0	cn dn	cd
	n	dc	−cs ds	0	m cd
	d	m'nc sc	−cs ns	−m cn sn	0

Con los teoremas de suma anteriores y para un m dado con 0 < m < 1, las funciones principales son, por tanto, soluciones de las siguientes ecuaciones diferenciales ordinarias no lineales:

${displaystyle operatorname {sn} (x)}$ resuelve las ecuaciones diferenciales ${displaystyle {frac {mathrm {d} ^{2}y}{mathrm {d} x^{2}}}+(1+m)y-2my^{3}=0}$ y ${displaystyle left({frac {mathrm {d} y}{mathrm {d} x}}right)^{2}=(1-y^{2})(1-my^{2})}$
${displaystyle operatorname {cn} (x)}$ resuelve las ecuaciones diferenciales ${displaystyle {frac {mathrm {d} ^{2}y}{mathrm {d} x^{2}}}+(1-2m)y+2my^{3}=0}$ y ${displaystyle left({frac {mathrm {d} y}{mathrm {d} x}}right)^{2}=(1-y^{2})(1-m+my^{2})}$
${displaystyle operatorname {dn} (x)}$ resuelve las ecuaciones diferenciales ${displaystyle {frac {mathrm {d} ^{2}y}{mathrm {d} x^{2}}}-(2-m)y+2y^{3}=0}$ y ${displaystyle left({frac {mathrm {d} y}{mathrm {d} x}}right)^{2}=(y^{2}-1)(1-m-y^{2})}$

La amplitud de Jacobi proporciona una solución no trivial de la ecuación diferencial que describe el movimiento exacto de un péndulo simple. En particular,

{displaystyle theta =2operatorname {am} left({frac {t{sqrt {2c}}}{2}},2right)rightarrow {frac {mathrm {d} ^{2}theta }{mathrm {d} t^{2}}}+csin theta =0.}

Una función que resuelve la ecuación diferencial del péndulo anterior con ángulo inicial $theta _{0}$ es

{displaystyle theta =2arcsin(koperatorname {cd} ({sqrt {c}}t,k^{2})),quad k=sin {frac {theta _{0}}{2}}.}

Expansión de la serie de Lambert en términos del nomo

Que el nomo sea ${displaystyle q=exp(-pi K'(m)/K(m))=e^{ipi tau }}$ , $0}" xmlns="http://www.w3.org/1998/Math/MathML">Im⁡ ⁡ ()τ τ )■0{displaystyle operatorname {Im} (tau)}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e16d11a64940d41b183400682406f3d721035c3d" style="vertical-align: -0.838ex; width:10.048ex; height:2.843ex;"/>$ , ${displaystyle m=k^{2}}$ y dejar ${displaystyle v=pi u/(2K(m))}$ . Luego las funciones tienen expansiones como la serie Lambert

{displaystyle operatorname {sn} (u,m)={frac {2pi }{kK(m)}}sum _{n=0}^{infty }{frac {q^{n+1/2}}{1-q^{2n+1}}}sin((2n+1)v),}

{displaystyle operatorname {cn} (u,m)={frac {2pi }{kK(m)}}sum _{n=0}^{infty }{frac {q^{n+1/2}}{1+q^{2n+1}}}cos((2n+1)v),}

{displaystyle operatorname {dn} (u,m)={frac {pi }{2K(m)}}+{frac {2pi }{K(m)}}sum _{n=1}^{infty }{frac {q^{n}}{1+q^{2n}}}cos(2nv)}

{displaystyle operatorname {zn} (u,m)={frac {2pi }{K(m)}}sum _{n=1}^{infty }{frac {q^{n}}{1-q^{2n}}}sin(2nv)}

cuando $<math alttext="{displaystyle qexp(2left|operatorname {Im} (v)right|)qexp ()2SilencioIm ()v)Silencio).1{displaystyle qexp(2left durableoperatorname {Im} (v)right habit) <img alt="{displaystyle qexp(2left|operatorname {Im} (v)right|)$ .

Para la amplitud de Jacobi,

{displaystyle operatorname {am} (u,m)={frac {pi u}{2K(m)}}+2sum _{n=1}^{infty }{frac {q^{n}}{n(1+q^{2n})}}sin(2nv)}

Donde $<math alttext="{displaystyle 0<m0.m.1{displaystyle 0 realizadasm <img alt="0<m$ y ${displaystyle uin mathbb {R} }$ .

Schett ha publicado expansiones de series de potencias bivariadas.

Cálculo rápido

Las razones de la función theta proporcionan una forma eficiente de calcular las funciones elípticas de Jacobi. Existe un método alternativo, basado en la media aritmético-geométrica y las transformaciones de Landen:

Inicializar

{displaystyle a_{0}=1,,b_{0}={sqrt {1-m}},c_{0}={sqrt {1-b_{0}^{2}}}}

Donde $<math alttext="{displaystyle 0<m0.m.1{displaystyle 0 realizadasm <img alt="0<m$ . Define

{displaystyle a_{n}={frac {a_{n-1}+b_{n-1}}{2}},,b_{n}={sqrt {a_{n-1}b_{n-1}}},,c_{n}={frac {a_{n-1}-b_{n-1}}{2}}}

Donde $ngeq 1$ . Entonces defina

{displaystyle varphi _{N}=2^{N}a_{N}u}

para ${displaystyle uin mathbb {R} }$ y un fijo $Nin {mathbb {N}}$ . Si

{displaystyle varphi _{n-1}={frac {1}{2}}left(varphi _{n}+arcsin left({frac {c_{n}}{a_{n}}}sin varphi _{n}right)right)}

para $ngeq 1$ , entonces

{displaystyle operatorname {am} (u,m)=varphi _{0}}

como $Nto infty$ . Esto es notable por su rápida convergencia. Entonces es trivial calcular todas las funciones elípticas Jacobi de la amplitud Jacobi ${displaystyle operatorname {am} }$ en la línea real.

Junto con los teoremas de suma para funciones elípticas (que son válidos para números complejos en general) y las transformaciones de Jacobi, el método de cálculo descrito anteriormente se puede utilizar para calcular todas las funciones elípticas de Jacobi en todo el plano complejo.

Otro método de cálculo rápido de las funciones elípticas de Jacobi mediante la media aritmético-geométrica, evitando el cálculo de la amplitud de Jacobi, se debe a Herbert E. Salzer:

Dejar

{displaystyle 0leq mleq 1,,0leq uleq K(m),,a_{0}=1,,b_{0}={sqrt {1-m}},}

{displaystyle a_{n+1}={frac {a_{n}+b_{n}}{2}},,b_{n+1}={sqrt {a_{n}b_{n}}},,c_{n+1}={frac {a_{n}-b_{n}}{2}}.}

Establecer

{displaystyle {begin{aligned}y_{N}&={frac {a_{N}}{sin(a_{N}u)}}\y_{N-1}&=y_{N}+{frac {a_{N}c_{N}}{y_{N}}}\y_{N-2}&=y_{N-1}+{frac {a_{N-1}c_{N-1}}{y_{N-1}}}\vdots &=vdots \y_{0}&=y_{1}+{frac {m}{4y_{1}}}.end{aligned}}}

Entonces

{displaystyle {begin{aligned}operatorname {sn} (u,m)&={frac {1}{y_{0}}}\operatorname {cn} (u,m)&={sqrt {1-{frac {1}{y_{0}^{2}}}}}\operatorname {dn} (u,m)&={sqrt {1-{frac {m}{y_{0}^{2}}}}}end{aligned}}}

como $Nto infty$ .

Aproximación en términos de funciones hiperbólicas

Las funciones elípticas de Jacobi se pueden ampliar en términos de las funciones hiperbólicas. Cuando $m$ está cerca de la unidad, tal que ${displaystyle m'^{2}}$ y poderes superiores $m'$ podemos ser descuidados, tenemos:

sn(u): ${displaystyle operatorname {sn} (u,m)approx tanh(u)+{frac {1}{4}}m'(sinh(u)cosh(u)-u)operatorname {sech} ^{2}(u).}$
cn(u): ${displaystyle operatorname {cn} (u,m)approx operatorname {sech} (u)-{frac {1}{4}}m'(sinh(u)cosh(u)-u)tanh(u)operatorname {sech} (u).}$
dn(u): ${displaystyle operatorname {dn} (u,m)approx operatorname {sech} (u)+{frac {1}{4}}m'(sinh(u)cosh(u)+u)tanh(u)operatorname {sech} (u).}$

Para la amplitud de Jacobi,

{displaystyle operatorname {am} (u,m)approx operatorname {gd} (u)+{frac {1}{4}}m'(sinh(u)cosh(u)-u)operatorname {sech} (u).}

Fracciones continuas

Suponiendo números reales ${displaystyle a,p}$ con $<math alttext="{displaystyle 0<a$

0.a.p{displaystyle 0 realizadasa<img alt="{displaystyle 0<a

y el nomo $q=e^{pi i tau}$ , $0}" xmlns="http://www.w3.org/1998/Math/MathML">Im⁡ ⁡ ()τ τ )■0{displaystyle operatorname {Im} (tau)}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e16d11a64940d41b183400682406f3d721035c3d" style="vertical-align: -0.838ex; width:10.048ex; height:2.843ex;"/>$ con módulo elíptico ${textstyle k(tau)={sqrt {1-k'(tau)^{2}}}=(vartheta _{10}(0;tau)/vartheta _{00}(0;tau))^{2}}$ . Si ${displaystyle K[tau ]=K(k(tau))}$ , donde ${displaystyle K(x)=pi /2cdot {}_{2}F_{1}(1/2,1/2;1;x^{2})}$ es la integral elíptica completa del primer tipo, luego mantiene la siguiente expansión de la fracción continua

{displaystyle {begin{aligned}&{frac {{textrm {dn}}left((p/2-a)tau Kleft[{frac {ptau }{2}}right];kleft({frac {ptau }{2}}right)right)}{sqrt {k'left({frac {ptau }{2}}right)}}}={frac {sum _{n=-infty }^{infty }q^{p/2n^{2}+(p/2-a)n}}{sum _{n=-infty }^{infty }(-1)^{n}q^{p/2n^{2}+(p/2-a)n}}}\[4pt]={}&-1+{frac {2}{1-{}}},{frac {q^{a}+q^{p-a}}{1-q^{p}+{}}},{frac {(q^{a}+q^{2p-a})(q^{a+p}+q^{p-a})}{1-q^{3p}+{}}},{frac {q^{p}(q^{a}+q^{3p-a})(q^{a+2p}+q^{p-a})}{1-q^{5p}+{}}},{frac {q^{2p}(q^{a}+q^{4p-a})(q^{a+3p}+q^{p-a})}{1-q^{7p}+{}}}cdots end{aligned}}}

fracciones continuas conocidas que implican ${displaystyle {textrm {sn}}(t),{textrm {cn}}(t)}$ y ${displaystyle {textrm {dn}}(t)}$ con módulo elíptico $k$ son

Para ${displaystyle zin mathbb {C} }$ , $<math alttext="{displaystyle |k|SilenciokSilencio.1{displaystyle Silenciok habit1} <img alt="{displaystyle |k|$ : pg. 374

{displaystyle int _{0}^{infty }{textrm {sn}}(t)e^{-tz},mathrm {d} t={frac {1}{1^{2}(1+k^{2})+z^{2}-{}}},{frac {1cdot 2^{2}cdot 3k^{2}}{3^{2}(1+k^{2})+z^{2}-{}}},{frac {3cdot 4^{2}cdot 5k^{2}}{5^{2}(1+k^{2})+z^{2}-{}}}cdots }

Para ${displaystyle zin mathbb {C} setminus {0}}$ , $<math alttext="{displaystyle |k|SilenciokSilencio.1{displaystyle Silenciok habit1} <img alt="{displaystyle |k|$ : pg. 375

{displaystyle int _{0}^{infty }{textrm {sn}}^{2}(t)e^{-tz},mathrm {d} t={frac {2z^{-1}}{2^{2}(1+k^{2})+z^{2}-{}}},{frac {2cdot 3^{2}cdot 4k^{2}}{4^{2}(1+k^{2})+z^{2}-{}}},{frac {4cdot 5^{2}cdot 6k^{2}}{6^{2}(1+k^{2})+z^{2}-{}}}cdots }

Para ${displaystyle zin mathbb {C} setminus {0}}$ , $<math alttext="{displaystyle |k|SilenciokSilencio.1{displaystyle Silenciok habit1} <img alt="{displaystyle |k|$ : pg. 220

{displaystyle int _{0}^{infty }{textrm {cn}}(t)e^{-tz},mathrm {d} t={frac {1}{z+{}}},{frac {1^{2}}{z+{}}},{frac {2^{2}k^{2}}{z+{}}},{frac {3^{2}}{z+{}}},{frac {4^{2}k^{2}}{z+{}}},{frac {5^{2}}{z+{}}}cdots }

Para ${displaystyle zin mathbb {C} setminus {0}}$ , $<math alttext="{displaystyle |k|SilenciokSilencio.1{displaystyle Silenciok habit1} <img alt="{displaystyle |k|$ : pg. 374

{displaystyle int _{0}^{infty }{textrm {dn}}(t)e^{-tz},mathrm {d} t={frac {1}{z+{}}},{frac {1^{2}k^{2}}{z+{}}},{frac {2^{2}}{z+{}}},{frac {3^{2}k^{2}}{z+{}}},{frac {4^{2}}{z+{}}},{frac {5^{2}k^{2}}{z+{}}}cdots }

Para ${displaystyle zin mathbb {C} }$ , $<math alttext="{displaystyle |k|SilenciokSilencio.1{displaystyle Silenciok habit1} <img alt="{displaystyle |k|$ : pg. 375

{displaystyle int _{0}^{infty }{frac {{textrm {sn}}(t){textrm {cn}}(t)}{{textrm {dn}}(t)}}e^{-tz},mathrm {d} t={frac {1}{2cdot 1^{2}(2-k^{2})+z^{2}-{}}},{frac {1cdot 2^{2}cdot 3k^{4}}{2cdot 3^{2}(2-k^{2})+z^{2}-{}}},{frac {3cdot 4^{2}cdot 5k^{4}}{2cdot 5^{2}(2-k^{2})+z^{2}-{}}}cdots }

Funciones inversas

Los inversos de las funciones elípticas Jacobi pueden definirse de manera similar a las funciones trigonométricas inversas; si ${displaystyle x=operatorname {sn} (xim)}$ , ${displaystyle xi =operatorname {arcsn} (x,m)}$ . Pueden ser representados como integrales elípticos, y se han encontrado representaciones de la serie de poder.

${displaystyle operatorname {arcsn} (x,m)=int _{0}^{x}{frac {mathrm {d} t}{sqrt {(1-t^{2})(1-mt^{2})}}}}$
${displaystyle operatorname {arccn} (x,m)=int _{x}^{1}{frac {mathrm {d} t}{sqrt {(1-t^{2})(1-m+mt^{2})}}}}$
${displaystyle operatorname {arcdn} (x,m)=int _{x}^{1}{frac {mathrm {d} t}{sqrt {(1-t^{2})(t^{2}+m-1)}}}}$

Proyección de mapas

La proyección quincuncial de Peirce es una proyección cartográfica basada en funciones elípticas jacobianas.

Contenido relacionado

Más resultados...