Función zeta de Riemann

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Función analítica en matemáticas

Función Riemann zeta

Especificaciones () z)

trazado con coloración de dominio.

El poste en

z=1

y dos ceros en la línea crítica.

La función zeta de Riemann o función zeta de Euler–Riemann, denotada por la letra griega $ζ$ (zeta), es una función matemática de una variable compleja definida como

{displaystyle zeta (s)=sum _{n=1}^{infty }{frac {1}{n^{s}}}={frac {1}{1^{s}}}+{frac {1}{2^{s}}}+{frac {1}{3^{s}}}+cdots }

1}" xmlns="http://www.w3.org/1998/Math/MathML">Re⁡ ⁡ ()s)■1{displaystyle operatorname {Re} (s)1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/82e22215d90eb4893d05f9b2bff409094a3451f2" style="vertical-align: -0.838ex; width:9.904ex; height:2.843ex;"/>

La función zeta de Riemann desempeña un papel fundamental en la teoría analítica de números y tiene aplicaciones en física, teoría de probabilidades y estadística aplicada.

Leonhard Euler introdujo y estudió por primera vez la función sobre los reales en la primera mitad del siglo XVIII. El artículo de Bernhard Riemann de 1859 "Sobre el número de primos menores que una magnitud dada" amplió la definición de Euler a una variable compleja, probó su continuación meromórfica y su ecuación funcional, y estableció una relación entre sus ceros y la distribución de los números primos. Este documento también contenía la hipótesis de Riemann, una conjetura sobre la distribución de ceros complejos de la función zeta de Riemann que muchos matemáticos consideran el problema sin resolver más importante de las matemáticas puras.

Euler calculó los valores de la función zeta de Riemann en números enteros positivos. El primero de ellos, $ζ (2)$ , proporciona una solución al problema de Basilea. En 1979, Roger Apéry demostró la irracionalidad de $ζ(3)$ . Los valores en puntos enteros negativos, también encontrados por Euler, son números racionales y juegan un papel importante en la teoría de las formas modulares. Se conocen muchas generalizaciones de la función zeta de Riemann, como la serie de Dirichlet, las funciones L de Dirichlet y las funciones L.

Definición

Artículo de Bernhard Riemann Sobre el número de primos por debajo de una magnitud dada

La función zeta de Riemann $ζ (s)$ es una función de una variable compleja $s = σ + it$ . (La notación $s$ , $σ$ , y $t$ se usa tradicionalmente en el estudio de la función zeta, siguiendo a Riemann). Cuando $Re(s) = σ > 1$ , la función se puede escribir como sumatoria convergente o integral:

{displaystyle zeta (s)=sum _{n=1}^{infty }{frac {1}{n^{s}}}={frac {1}{Gamma (s)}}int _{0}^{infty }{frac {x^{s-1}}{e^{x}-1}},mathrm {d} x,,}

dónde

{displaystyle Gamma (s)=int _{0}^{infty }x^{s-1},e^{-x},mathrm {d} x}

es la función gamma. La función zeta de Riemann se define para otros valores complejos a través de la continuación analítica de la función definida para $σ > 1$ .

Leonhard Euler consideró la serie anterior en 1740 para valores enteros positivos $s$ , y más tarde Chebyshev extendió la definición a $1.}" xmlns="http://www.w3.org/1998/Math/MathML">Re⁡ ⁡ ()s)■1.{displaystyle operatorname {Re} (s) confianza1.}1.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c05b7a57c920e79cf69fec018eeb50fa62627788" style="vertical-align: -0.838ex; width:10.55ex; height:2.843ex;"/>$

La serie anterior es una serie prototípica de Dirichlet que converge absolutamente a una función analítica para $s$ tal que σ > 1 y diverge para todos los demás valores de $s$ . Riemann demostró que la función definida por la serie en el semiplano de convergencia puede continuarse analíticamente hasta todos los valores complejos $s \neq 1$ . Para $s = 1$ , la serie es la serie armónica que diverge a $+\infty$ , y

{displaystyle lim _{sto 1}(s-1)zeta (s)=1.}

s = 1

1

Fórmula del producto de Euler

En 1737, la conexión entre la función zeta y los números primos fue descubierta por Euler, quien demostró la identidad

sum _{n=1}^{infty }{frac {1}{n^{s}}}=prod _{p{text{ prime}}}{frac {1}{1-p^{-s}}},

donde, por definición, el lado izquierdo es $ζ (s)$ y el producto infinito a la derecha El lado de la mano se extiende sobre todos los números primos $p$ (estas expresiones se denominan productos de Euler):

{displaystyle prod _{p{text{ prime}}}{frac {1}{1-p^{-s}}}={frac {1}{1-2^{-s}}}cdot {frac {1}{1-3^{-s}}}cdot {frac {1}{1-5^{-s}}}cdot {frac {1}{1-7^{-s}}}cdot {frac {1}{1-11^{-s}}}cdots {frac {1}{1-p^{-s}}}cdots }

Ambos lados de la fórmula del producto de Euler convergen para $Re(s) > 1$ . La prueba de la identidad de Euler utiliza únicamente la fórmula de la serie geométrica y el teorema fundamental de la aritmética. Dado que la serie armónica, obtenida cuando $s = 1$ , diverge, la fórmula de Euler (que se convierte en $Π p p / p - 1$ ) implica que hay infinitas muchos primos.

La fórmula del producto de Euler se puede utilizar para calcular la probabilidad asintótica de que $s$ enteros seleccionados al azar sean coprimos entre conjuntos. Intuitivamente, la probabilidad de que cualquier número individual sea divisible por un primo (o cualquier número entero) $p$ es $1 / p$ . Por lo tanto, la probabilidad de que los números $s$ sean todos divisibles por este número primo es $1 / p s$ , y el la probabilidad de que al menos uno de ellos no es $1 - 1 / p s$ . Ahora, para primos distintos, estos eventos de divisibilidad son mutuamente independientes porque los divisores candidatos son coprimos (un número es divisible por divisores coprimos $n$ y $m$ si y solo si es divisible por $nm$ , un evento que ocurre con probabilidad $1 / nm$ ). Por lo tanto, la probabilidad asintótica de que los números $s$ sean coprimos está dada por un producto de todos los números primos,

{displaystyle prod _{p{text{ prime}}}left(1-{frac {1}{p^{s}}}right)=left(prod _{p{text{ prime}}}{frac {1}{1-p^{-s}}}right)^{-1}={frac {1}{zeta (s)}}.}

Ecuación funcional de Riemann

Esta función zeta satisface la ecuación funcional

{displaystyle zeta (s)=2^{s}pi ^{s-1} sin left({frac {pi s}{2}}right) Gamma (1-s) zeta (1-s),}

. s)

s

1 - s

Especificaciones () s)

s = 2 n

ceros triviales

Especificaciones () s)

s

pecado(πs / 2) s)

. s)

Prueba de la ecuación funcional de Riemann

Una prueba de la ecuación funcional procede como sigue: Observamos que si $0}" xmlns="http://www.w3.org/1998/Math/MathML">σ σ ■0{displaystyle sigma œ0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/762ecd0f0905dd0d4d7a07f80fa8bfb324b9b021" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>$ , entonces

{displaystyle int _{0}^{infty }x^{{1 over 2}{s}-1}e^{-n^{2}pi x},dx={Gamma left({s over 2}right) over {n^{s}pi ^{s over 2}}}.}

Como resultado, si $1}" xmlns="http://www.w3.org/1998/Math/MathML">σ σ ■1{displaystyle sigma >}1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4244926d1b580be0f7872e3004da65efb48536" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>$ entonces

{displaystyle {frac {Gamma left({frac {s}{2}}right)zeta (s)}{pi ^{s/2}}}=sum _{n=1}^{infty }int _{0}^{infty }x^{{s over 2}-1}e^{-n^{2}pi x},dx=int _{0}^{infty }x^{{s over 2}-1}sum _{n=1}^{infty }e^{-n^{2}pi x},dx,}

con la inversión de los procesos limitantes justificados por la convergencia absoluta (de ahí el requisito más estricto

sigma

Por conveniencia, deja

{displaystyle psi (x):=sum _{n=1}^{infty }e^{-n^{2}pi x}.}

Entonces...

{displaystyle zeta (s)={pi ^{s over 2} over Gamma ({s over 2})}int _{0}^{infty }x^{{1 over 2}{s}-1}psi (x),dx.}

Por la fórmula de summación Poisson tenemos

{displaystyle sum _{n=-infty }^{infty }{e^{-n^{2}pi x}}={1 over {sqrt {x}}}sum _{n=-infty }^{infty }{e^{-n^{2}pi over x}},}

así

{displaystyle 2psi (x)+1={1 over {sqrt {x}}}left{2psi left({1 over x}right)+1right}.}

Por lo tanto

{displaystyle pi ^{-{s over 2}}Gamma left({s over 2}right)zeta (s)=int _{0}^{1}x^{{s over 2}-1}psi (x),dx+int _{1}^{infty }x^{{s over 2}-1}psi (x),dx.}

Esto equivale a

{displaystyle int _{0}^{1}x^{{s over 2}-1}left{{1 over {sqrt {x}}}psi left({1 over x}right)+{1 over 2{sqrt {x}}}-{1 over 2}right},dx+int _{1}^{infty }x^{{s over 2}-1}psi (x),dx}

{displaystyle {1 over {s-1}}-{1 over s}+int _{0}^{1}x^{{s over 2}-{3 over 2}}psi left({1 over x}right),dx+int _{1}^{infty }x^{{s over 2}-1}psi (x),dx.}

Así que...

{displaystyle pi ^{-{s over 2}}Gamma left({s over 2}right)zeta (s)={1 over {s({s-1})}}+int _{1}^{infty }left({x^{-{{s} over 2}-{1 over 2}}+x^{{{s} over 2}-1}}right)psi (x),dx}

que es convergente para todos s, así que sostiene la continuación analítica. Además, el RHS no cambia si s se cambia a 1 −s. Por lo tanto

{displaystyle pi ^{-{s over 2}}Gamma left({s over 2}right)zeta (s)=pi ^{-{1 over 2}+{s over 2}}Gamma left({1 over 2}-{s over 2}right)zeta (1-s)}

que es la ecuación funcional. E. C. Titchmarsh (1986). The The Theory of the Riemann Zeta-function (2a edición). Oxford: Oxford Science Publications. pp. 21–22. ISBN 0-19-853369-1. Atribuido a Bernhard Riemann.

La ecuación funcional fue establecida por Riemann en su artículo de 1859 "Sobre el número de primos menores que una magnitud dada" y se utiliza para construir la continuación analítica en primer lugar. Euler había conjeturado una relación equivalente más de cien años antes, en 1749, para la función eta de Dirichlet (la función zeta alterna):

{displaystyle eta (s)=sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n^{s}}}=left(1-{2^{1-s}}right)zeta (s).}

Dicho sea de paso, esta relación proporciona una ecuación para calcular $ζ (s)$ en la región 0 < $Re(s)$ < 1, es decir

{displaystyle zeta (s)={frac {1}{1-{2^{1-s}}}}sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n^{s}}}}

s ■ 0

Riemann también encontró una versión simétrica de la ecuación funcional que se aplica a la función xi:

{displaystyle xi (s)={frac {1}{2}}pi ^{-{frac {s}{2}}}s(s-1)Gamma left({frac {s}{2}}right)zeta (s),}

{displaystyle xi (s)=xi (1-s).}

(La ξ(t) original de Riemann era ligeramente diferente).

El ${displaystyle pi ^{-s/2}Gamma (s/2)}$ El factor no fue bien entendido en el momento de Riemann, hasta la tesis de John Tate (1950), en la que se demostró que este denominado "factor gamma" es, de hecho, el factor L local correspondiente al lugar Arquimedean, los otros factores en la expansión del producto Euler son los L-factores locales de los lugares no arquimedeos.

Ceros, la recta crítica y la hipótesis de Riemann

La función Riemann zeta no tiene ceros a la derecha de

σ = 1

o (aparte de los ceros triviales) a la izquierda de

σ = 0

(ni los ceros pueden estar demasiado cerca de esas líneas). Además, los ceros no-triviales son simétricos sobre el eje real y la línea

σ = 1 / 2

y, según la hipótesis de Riemann, todos están en la línea

σ = 1 / 2

Esta imagen muestra una trama de la función Riemann zeta a lo largo de la línea crítica para los valores reales de

t

corriendo de 0 a 34. Los primeros cinco ceros en la tira crítica son claramente visibles como el lugar donde las espirales pasan por el origen.

La parte real (rojo) e parte imaginaria (azul) de la función Riemann zeta a lo largo de la línea crítica Re(s) = 1/2. Los primeros ceros no-triviales se pueden ver en Im(s) = ±14.135, ±21.022 y ±25.011.

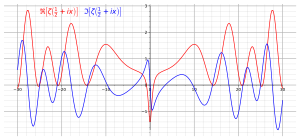
La ecuación funcional muestra que la función Riemann zeta tiene ceros en - 2, 4, 4.... Estos se llaman ceros triviales. Son triviales en el sentido de que su existencia es relativamente fácil de probar, por ejemplo, de $pecado π s / 2$ estar 0 en la ecuación funcional. Los ceros no-triviales han captado mucha más atención porque su distribución no sólo es mucho menos comprendida, sino, lo que es más importante, su estudio produce importantes resultados relativos a números primos y objetos relacionados en la teoría de números. Se sabe que cualquier cero no-trivial está en la tira abierta $<math alttext="{displaystyle {sin mathbb {C}:0<operatorname {Re} (s){}s▪ ▪ C:0.Re ()s).1}{displaystyle {sin mathbb {C}:0 Se hizo 'operatorname {Re} (s) <img alt="{displaystyle {sin mathbb {C}:0<operatorname {Re} (s)$ , que se llama el tira crítica. El set ${displaystyle {sin mathbb {C}:operatorname {Re} (s)=1/2}}$ se llama línea crítica. La hipótesis Riemann, considerada uno de los mayores problemas sin resolver en las matemáticas, afirma que todos los ceros no-triviales están en la línea crítica. En 1989, Conrey demostró que más del 40% de los ceros no-triviales de la función Riemann zeta están en la línea crítica.

Para la función zeta de Riemann en la línea crítica, consulte Función Z.

Primero pocos ceros notriviales
Cero
1/2 ± 14.134725 i
1/2 ± 21.022040 i
1/2 ± 25.010858 i
1/2 ± 30.424876 i
1/2 ± 32,935062 i
1/2 ± 37.586178 i

Número de ceros en la tira crítica

Vamos $N(T)$ ser el número de ceros de $zeta (s)$ en la tira crítica $<math alttext="{displaystyle 0<operatorname {Re} (s)0.Re ()s).1{displaystyle 0 realizadasoperatorname {Re} (s) realizadas1} <img alt="{displaystyle 0<operatorname {Re} (s)$ , cuyas partes imaginarias están en el intervalo $<math alttext="{displaystyle 0<operatorname {Im} (s)0.Im ()s).T{displaystyle 0 realizadasoperatorname {Im} (s) <img alt="{displaystyle 0<operatorname {Im} (s)$ . Trudgian demostró que, si $e}" xmlns="http://www.w3.org/1998/Math/MathML">T■e{displaystyle T]e}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4177c581663e58522b046e394e064040d09c6071" style="vertical-align: -0.338ex; width:5.818ex; height:2.176ex;"/>$ , entonces

{displaystyle |N(T)-{frac {T}{2pi }}log {frac {T}{2pi e}}|leq 0.112log T+0.278log log T+3.385+{frac {0.2}{T}}}

Las conjeturas de Hardy-Littlewood

En 1914, Godfrey Harold Hardy demostró que $ζ (1 / 2 + eso)$ tiene infinitos ceros reales.

Hardy y John Edensor Littlewood formularon dos conjeturas sobre la densidad y la distancia entre los ceros de $ζ (1 / 2 + it)$ en intervalos de grandes números reales positivos. A continuación, $N (T)$ es el número total de ceros reales y $N 0 (T)$ el número total de ceros de orden impar de la función $ζ (1 / 2 + eso)$ que se encuentra en el intervalo $(0, T]$ .

Para cualquier $ε ■ 0$ , existe un $T 0 () ε) 0$ tal cuando
${displaystyle Tgeq T_{0}(varepsilon)quad {text{ and }}quad H=T^{{frac {1}{4}}+varepsilon },}$
el intervalo $() T, T + H]$ contiene un cero de orden extraño.
Para cualquier $ε ■ 0$ , existe un $T 0 () ε) 0$ y $c ε ■ 0$ tal que la desigualdad
$N_{0}(T+H)-N_{0}(T)geq c_{varepsilon }H$
sostiene cuando
${displaystyle Tgeq T_{0}(varepsilon)quad {text{ and }}quad H=T^{{frac {1}{2}}+varepsilon }.}$

Estas dos conjeturas abrieron nuevas direcciones en la investigación de la función zeta de Riemann.

Región libre de cero

La ubicación de los ceros de la función Riemann zeta es de gran importancia en la teoría de números. El teorema número primo es equivalente al hecho de que no hay ceros de la función zeta en el $Re(s) = 1$ línea. Un mejor resultado que sigue de una forma efectiva del teorema de valor medio de Vinogradov es que $Especificaciones () σ + es)$ siempre ${displaystyle sigma geq 1-{frac {1}{57.54(log {|t|})^{frac {2}{3}}(log {log {|t|}})^{frac {1}{3}}}}}$ y $Silencio t \geq 3$ .

En 2015, Mossinghoff y Trudgian demostraron que zeta no tiene ceros en la región.

{displaystyle sigma geq 1-{frac {1}{5.573412log |t|}}}

para $Silencio t \geq 2$ . Esta es la región más conocida sin cero en la tira crítica para $<math alttext="{displaystyle 3.06cdot 10^{10}<|t|3.06⋅ ⋅ 1010.SilenciotSilencio.exp⁡ ⁡ ()10151.5).. 5,5⋅ ⋅ 104408{displaystyle 3.06cdot 10^{10}Seguido en silencio significadoexp(10151.5)approx 5.5cdot 10^{4408}<img alt="{displaystyle 3.06cdot 10^{10}<|t|$ .

El resultado más fuerte de este tipo que uno puede esperar es la verdad de la hipótesis de Riemann, que tendría muchas consecuencias profundas en la teoría de los números.

Otros resultados

Se sabe que hay infinitos ceros en la línea crítica. Littlewood demostró que si la secuencia ( $γ n$ ) contiene las partes imaginarias de todos los ceros en el semiplano superior en orden ascendente, entonces

{displaystyle lim _{nrightarrow infty }left(gamma _{n+1}-gamma _{n}right)=0.}

El teorema de la línea crítica afirma que una proporción positiva de los ceros no triviales se encuentra en la línea crítica. (La hipótesis de Riemann implicaría que esta proporción es 1.)

En la tira crítica, el cero con la parte imaginaria no negativa más pequeña es $1 / 2 + 14.13472514... i$ (OEIS: A058303). El hecho de que

zeta (s)={overline {zeta ({overline {s}})}}

para todos los $s \neq 1$ complejos implica que los ceros de la función zeta de Riemann son simétricos con respecto al eje real. Además, al combinar esta simetría con la ecuación funcional, se ve que los ceros no triviales son simétricos con respecto a la línea crítica $Re(s) = 1 / 2$ .

También se sabe que no hay ceros en una línea con la parte real 1.

Valores específicos

Para cualquier número entero par positivo $2 n$ ,

{displaystyle zeta (2n)={frac {(-1)^{n+1}B_{2n}(2pi)^{2n}}{2(2n)!}},}

B 2 n

2 n

K

Para enteros no positivos, uno tiene

{displaystyle zeta (-n)=(-1)^{n}{frac {B_{n+1}}{n+1}}}

n \geq 0

B 1 = 1 / 2

Especificaciones

B m = 0

m

A través de la continuación analítica, se puede demostrar que

{displaystyle zeta (-1)=-{tfrac {1}{12}}}

{displaystyle zeta (0)=-{tfrac {1}{2}}}

El valor

{displaystyle zeta {bigl (}{tfrac {1}{2}}{bigr)}=-1.46035450880958681288ldots }

Aunque

{displaystyle zeta (1)=1+{tfrac {1}{2}}+{tfrac {1}{3}}+cdots }

{displaystyle lim _{varepsilon to 0}{frac {zeta (1+varepsilon)+zeta (1-varepsilon)}{2}}}

γ = 0,572...

La demostración del valor particular

{displaystyle zeta (2)=1+{frac {1}{2^{2}}}+{frac {1}{3^{2}}}+cdots ={frac {pi ^{2}}{6}}}

¿Cuál es la probabilidad de que dos números seleccionados al azar sean relativamente primos?

{displaystyle zeta (3)=1+{frac {1}{2^{3}}}+{frac {1}{3^{3}}}+cdots =1.202056903159594285399...}

Tomando el límite ${displaystyle srightarrow +infty }$ a través de los números reales, uno obtiene ${displaystyle zeta (+infty)=1}$ . Pero al infinito complejo en la esfera Riemann la función zeta tiene una singularidad esencial.

Varias propiedades

Para sumas que involucran la función zeta en valores enteros y semienteros, consulte series zeta racionales.

Recíproco

El recíproco de la función zeta puede expresarse como una serie de Dirichlet sobre la función de Möbius $μ (n)$ :

frac{1}{zeta(s)} = sum_{n=1}^infty frac{mu(n)}{n^s}

para cada número complejo $s$ con parte real mayor que 1. Hay una serie de relaciones similares que involucran varias conocidas funciones multiplicativas; estos se dan en el artículo sobre la serie de Dirichlet.

La hipótesis de Riemann es equivalente a afirmar que esta expresión es válida cuando la parte real de $s$ es mayor que 1/2.

Universalidad

La franja crítica de la función zeta de Riemann tiene la notable propiedad de universalidad. Esta universalidad de la función zeta establece que existe alguna ubicación en la franja crítica que se aproxima arbitrariamente bien a cualquier función holomorfa. Dado que las funciones holomorfas son muy generales, esta propiedad es bastante notable. Sergei Mikhailovitch Voronin proporcionó la primera prueba de universalidad en 1975. El trabajo más reciente ha incluido versiones efectivas del teorema de Voronin y su extensión a las funciones L de Dirichlet.

Estimaciones del máximo del módulo de la función zeta

Sean las funciones $F (T; H)$ y $G (s 0;Δ)$ definido por las igualdades

{displaystyle F(T;H)=max _{|t-T|leq H}left|zeta left({tfrac {1}{2}}+itright)right|,qquad G(s_{0};Delta)=max _{|s-s_{0}|leq Delta }|zeta (s)|.}

Aquí $T$ es un número positivo suficientemente grande, $0 < H ≪ registro registro T$ , $s 0 = σ 0 + iT$ , $1 / 2 \leq σ 0 \leq 1$ , $0 < Delta < 1 / 3$ . Estimando los valores $F$ y $G$ de abajo muestra qué tan grandes (en módulo) los valores $ζ (s)$ pueden tomar en intervalos cortos de la línea crítica o en pequeñas vecindades de puntos que se encuentran en la franja crítica $0 \leq Re(s) \leq 1$ .

El caso $H ≫ log log T$ fue estudiado por Kanakanahalli Ramachandra; el caso $Δ > c$ , donde $c$ es una constante suficientemente grande, es trivial.

Anatolii Karatsuba demostró, en particular, que si los valores $H$ y $Δ$ exceda ciertas constantes suficientemente pequeñas, entonces las estimaciones

{displaystyle F(T;H)geq T^{-c_{1}},qquad G(s_{0};Delta)geq T^{-c_{2}},}

mantener, donde $c 1$ y $c 2$ son ciertas constantes absolutas.

El argumento de la función zeta de Riemann

La función

{displaystyle S(t)={frac {1}{pi }}arg {zeta left({tfrac {1}{2}}+itright)}}

se llama el argumento de la función zeta de Riemann. Aquí $arg ζ (1 / 2 + it)$ es el incremento de una rama continua arbitraria de $arg ζ (s)$ a lo largo de la línea discontinua que une los puntos $2$ , $2 + it$ y $1 / 2 + it$ .

Hay algunos teoremas sobre las propiedades de la función $S (t)$ . Entre esos resultados se encuentran los teoremas del valor medio para $S (t)$ y su primera integral

{displaystyle S_{1}(t)=int _{0}^{t}S(u),mathrm {d} u}

sobre los intervalos de la recta real, y también el teorema que afirma que todo intervalo $(T, T + H]$ para

H ge T^{frac{27}{82}+varepsilon}

contiene al menos

{displaystyle H{sqrt[{3}]{ln T}}e^{-c{sqrt {ln ln T}}}}

puntos donde la función $S (t)$ cambia de signo. Atle Selberg obtuvo resultados similares anteriores para el caso

{displaystyle Hgeq T^{{frac {1}{2}}+varepsilon }.}

Representaciones

Serie de Dirichlet

Se puede obtener una extensión del área de convergencia reorganizando la serie original. Las series

zeta (s)={frac {1}{s-1}}sum _{n=1}^{infty }left({frac {n}{(n+1)^{s}}}-{frac {n-s}{n^{s}}}right)

converge para $Re(s) > 0$ , mientras

zeta (s)={frac {1}{s-1}}sum _{n=1}^{infty }{frac {n(n+1)}{2}}left({frac {2n+3+s}{(n+1)^{s+2}}}-{frac {2n-1-s}{n^{s+2}}}right)

converge incluso para $Re(s) > -1$ . De esta forma, el área de convergencia puede extenderse a $Re(s) > - k$ para cualquier entero negativo $- k$ .

Integrales tipo Mellin

La transformada de Mellin de una función $f (x)$ se define como

{displaystyle int _{0}^{infty }f(x)x^{s},{frac {mathrm {d} x}{x}}}

en la región donde se define la integral. Hay varias expresiones para la función zeta como integrales tipo transformada de Mellin. Si la parte real de $s$ es mayor que uno, tenemos

{displaystyle Gamma (s)zeta (s)=int _{0}^{infty }{frac {x^{s-1}}{e^{x}-1}},mathrm {d} xquad }

{displaystyle quad Gamma (s)zeta (s)={frac {1}{2s}}int _{0}^{infty }{frac {x^{s}}{cosh(x)-1}},mathrm {d} x}

donde $Γ$ denota la función gamma. Al modificar el contorno, Riemann demostró que

{displaystyle 2sin(pi s)Gamma (s)zeta (s)=ioint _{H}{frac {(-x)^{s-1}}{e^{x}-1}},mathrm {d} x}

para todos los $s$ (donde $H$ denota el contorno de Hankel).

También podemos encontrar expresiones relacionadas con los números primos y el teorema de los números primos. Si $π (x)$ es la función de conteo de números primos, entonces

{displaystyle ln zeta (s)=sint _{0}^{infty }{frac {pi (x)}{x(x^{s}-1)}},mathrm {d} x,}

para valores con $Re(s) > 1$ .

Una transformada de Mellin similar implica la función de Riemann $J (x)$ , que cuenta las potencias principales $p n$ con un peso de $1 / n$ , de modo que

{displaystyle J(x)=sum {frac {pi left(x^{frac {1}{n}}right)}{n}}.}

Ahora

{displaystyle ln zeta (s)=sint _{0}^{infty }J(x)x^{-s-1},mathrm {d} x.}

Estas expresiones se pueden utilizar para demostrar el teorema de los números primos mediante la transformada inversa de Mellin. Es más fácil trabajar con la función de conteo de primos de Riemann, y $π (x)$ se puede recuperar de por inversión de Möbius.

Funciones theta

La función zeta de Riemann se puede dar mediante una transformada de Mellin

{displaystyle 2pi ^{-{frac {s}{2}}}Gamma left({frac {s}{2}}right)zeta (s)=int _{0}^{infty }{bigl (}theta (it)-1{bigr)}t^{{frac {s}{2}}-1},mathrm {d} t,}

en términos de la función theta de Jacobi

{displaystyle theta (tau)=sum _{n=-infty }^{infty }e^{pi in^{2}tau }.}

Sin embargo, esta integral solo converge si la parte real de $s$ es mayor que 1, pero se puede regularizar. Esto da la siguiente expresión para la función zeta, que está bien definida para todos los $s$ excepto 0 y 1:

{displaystyle pi ^{-{frac {s}{2}}}Gamma left({frac {s}{2}}right)zeta (s)={frac {1}{s-1}}-{frac {1}{s}}+{frac {1}{2}}int _{0}^{1}left(theta (it)-t^{-{frac {1}{2}}}right)t^{{frac {s}{2}}-1},mathrm {d} t+{frac {1}{2}}int _{1}^{infty }{bigl (}theta (it)-1{bigr)}t^{{frac {s}{2}}-1},mathrm {d} t.}

Serie Laurent

La función zeta de Riemann es meromórfica con un solo polo de orden uno en $s = 1$ . Por lo tanto, se puede expandir como una serie de Laurent sobre $s = 1$ ; el desarrollo de la serie es entonces

{displaystyle zeta (s)={frac {1}{s-1}}+sum _{n=0}^{infty }{frac {gamma _{n}}{n!}}(1-s)^{n}.}

Las constantes $γ n$ aquí se denominan constantes de Stieltjes y se pueden definir por el limite

{displaystyle gamma _{n}=lim _{mrightarrow infty }{left(left(sum _{k=1}^{m}{frac {(ln k)^{n}}{k}}right)-{frac {(ln m)^{n+1}}{n+1}}right)}.}

El término constante $γ 0$ es la constante de Euler-Mascheroni.

Integrales

Para todos los $s \in C$ , $s \neq 1$ , la relación integral (cf. fórmula de Abel-Plana)

{displaystyle zeta (s)={frac {1}{s-1}}+{frac {1}{2}}+2int _{0}^{infty }{frac {sin(sarctan t)}{left(1+t^{2}right)^{s/2}left(e^{2pi t}-1right)}},mathrm {d} t}

es cierto, lo que puede usarse para una evaluación numérica de la función zeta.

Factorial ascendente

Otro desarrollo de series usando el factorial ascendente válido para todo el plano complejo es

{displaystyle zeta (s)={frac {s}{s-1}}-sum _{n=1}^{infty }{bigl (}zeta (s+n)-1{bigr)}{frac {s(s+1)cdots (s+n-1)}{(n+1)!}}.}

Esto se puede usar recursivamente para extender la definición de la serie de Dirichlet a todos los números complejos.

La función zeta de Riemann también aparece en una forma similar a la transformada de Mellin en una integral sobre el operador Gauss-Kuzmin-Wirsing que actúa sobre $x s - 1$ ; ese contexto da lugar a una expansión en serie en términos del factorial descendente.

Producto Hadamard

Sobre la base del teorema de factorización de Weierstrass, Hadamard dio la expansión del producto infinito

{displaystyle zeta (s)={frac {e^{left(log(2pi)-1-{frac {gamma }{2}}right)s}}{2(s-1)Gamma left(1+{frac {s}{2}}right)}}prod _{rho }left(1-{frac {s}{rho }}right)e^{frac {s}{rho }},}

donde el producto está sobre los ceros no triviales $ρ$ de $ζ$ y la letra $γ$ nuevamente denota la constante de Euler-Mascheroni. Una expansión de producto infinito más simple es

{displaystyle zeta (s)=pi ^{frac {s}{2}}{frac {prod _{rho }left(1-{frac {s}{rho }}right)}{2(s-1)Gamma left(1+{frac {s}{2}}right)}}.}

Esta forma muestra claramente el polo simple en $s = 1$ , los ceros triviales en −2, −4,... debido a la término de la función gamma en el denominador y los ceros no triviales en $s = ρ$ . (Para garantizar la convergencia en la última fórmula, el producto debe tomarse sobre 'pares coincidentes' de ceros, es decir, los factores para un par de ceros de la forma $ρ$ y $1 - ρ$ deben combinarse).

Serie globalmente convergente

Una serie globalmente convergente para la función zeta, válida para todos los números complejos $s$ excepto $s = 1 + 2π i / ln 2 n$ para algún número entero $n$ , fue conjeturado por Konrad Knopp en 1926 y probado por Helmut Hasse en 1930 (cf. resumen de Euler):

{displaystyle zeta (s)={frac {1}{1-2^{1-s}}}sum _{n=0}^{infty }{frac {1}{2^{n+1}}}sum _{k=0}^{n}{binom {n}{k}}{frac {(-1)^{k}}{(k+1)^{s}}}.}

La serie apareció en un apéndice del artículo de Hasse y fue publicada por segunda vez por Jonathan Sondow en 1994.

<pHase también probó la serie globalmente convergente

{displaystyle zeta (s)={frac {1}{s-1}}sum _{n=0}^{infty }{frac {1}{n+1}}sum _{k=0}^{n}{binom {n}{k}}{frac {(-1)^{k}}{(k+1)^{s-1}}}}

en la misma publicación. Investigación de Iaroslav Blagouchine descubrió que Joseph Ser publicó una serie similar y equivalente en 1926.

Peter Borwein ha desarrollado un algoritmo que aplica polinomios de Chebyshev a la función eta de Dirichlet para producir una serie convergente muy rápida adecuada para cálculos numéricos de alta precisión.

Representación de series en enteros positivos a través del primorial

{displaystyle zeta (k)={frac {2^{k}}{2^{k}-1}}+sum _{r=2}^{infty }{frac {(p_{r-1}#)^{k}}{J_{k}(p_{r}#)}}qquad k=2,3,ldots.}

Aquí $p n #$ es la secuencia primordial y $J k$ es la función totient de Jordan.

Representación de series por los números poli-Bernoulli incompletos

La función $ζ$ se puede representar, por $Re(s) > 1$ , por la serie infinita

${displaystyle zeta (s)=sum _{n=0}^{infty }B_{n,geq 2}^{(s)}{frac {(W_{k}(-1))^{n}}{n!}},}$

donde $k \in {-1, 0}$ , $W k$ es la $k$ ésima rama de la función W de Lambert, y $B (μ) n, \geq2$ es un número poli-Bernoulli incompleto.

La transformada de Mellin del mapa de Engel

La función ${displaystyle g(x)=xleft(1+leftlfloor x^{-1}rightrfloor right)-1}$ es iterado para encontrar los coeficientes que aparecen en las expansiones de Engel.

La transformación de Mellin del mapa $g(x)$ está relacionado con la función Riemann zeta por la fórmula

${displaystyle {begin{aligned}int _{0}^{1}g(x)x^{s-1},dx&=sum _{n=1}^{infty }int _{frac {1}{n+1}}^{frac {1}{n}}(x(n+1)-1)x^{s-1},dx\[6pt]&=sum _{n=1}^{infty }{frac {n^{-s}(s-1)+(n+1)^{-s-1}(n^{2}+2n+1)+n^{-s-1}s-n^{1-s}}{(s+1)s(n+1)}}\[6pt]&={frac {zeta (s+1)}{s+1}}-{frac {1}{s(s+1)}}end{aligned}}}$

Secuencia Thue-Morse

Ciertas combinaciones lineales de series de Dirichlet cuyos coeficientes son términos de la sucesión de Thue-Morse dan lugar a identidades que involucran la función Riemann Zeta (Tóth, 2022). Por ejemplo:

${displaystyle {begin{aligned}sum _{ngeq 1}{frac {5t_{n-1}+3t_{n}}{n^{2}}}&=4zeta (2)={frac {2pi ^{2}}{3}},\sum _{ngeq 1}{frac {9t_{n-1}+7t_{n}}{n^{3}}}&=8zeta (3),end{aligned}}}$

Donde ${displaystyle (t_{n})_{ngeq 0}}$ es ${displaystyle n^{rm {th}}}$ término de la secuencia Thue-Morse. De hecho, para todos $s$ con parte real mayor que $1$ , tenemos

${displaystyle (2^{s}+1)sum _{ngeq 1}{frac {t_{n-1}}{n^{s}}}+(2^{s}-1)sum _{ngeq 1}{frac {t_{n}}{n^{s}}}=2^{s}zeta (s).}$

Algoritmos numéricos

Un algoritmo clásico, en uso antes de 1930, aplica la fórmula de Euler-Maclaurin para obtener, para n y m enteros positivos,

${displaystyle zeta (s)=sum _{j=1}^{n-1}j^{-s}+{tfrac {1}{2}}n^{-s}+{frac {n^{1-s}}{s-1}}+sum _{k=1}^{m}T_{k,n}(s)+E_{m,n}(s)}$

¿Dónde? $B_{{2k}}$ denota el número indicado de Bernoulli,

${displaystyle T_{k,n}(s)={frac {B_{2k}}{(2k)!}}n^{1-s-2k}prod _{j=0}^{2k-2}(s+j)}$

y el error satisface

$<math alttext="{displaystyle |E_{m,n}(s)|SilencioEm,n()s)Silencio.Silencios+2m+1σ σ +2m+1Tm+1,n()s)Silencio,{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {s+2m+1}{sigma ##2m+1}T_{m+1,n}(s)right sometida,}<img alt="{displaystyle |E_{m,n}(s)|$

con σ = Re(s).

Un algoritmo numérico moderno es el algoritmo de Odlyzko-Schönhage.

Aplicaciones

La función zeta ocurre en las estadísticas aplicadas (consulte la ley de Zipf y la ley de Zipf-Mandelbrot).

La regularización de la función Zeta se utiliza como un medio posible de regularización de series divergentes e integrales divergentes en la teoría cuántica de campos. En un ejemplo notable, la función zeta de Riemann aparece explícitamente en un método para calcular el efecto Casimir. La función zeta también es útil para el análisis de sistemas dinámicos.

Afinación Musical

En la teoría de los afinamientos musicales, la función zeta se puede utilizar para encontrar divisiones iguales de la octava (EDOs) que aproximan de cerca los intervalos de la serie armónica. Para aumentar los valores $tin mathbb {R}$ , el valor de

${displaystyle leftvert zeta left({frac {1}{2}}+{frac {2pi {i}}{ln {(2)}}}tright)rightvert }$

picos cerca de números enteros que corresponden a tales EDO. Los ejemplos incluyen opciones populares como 12, 19 y 53.

Serie infinita

La función zeta evaluada en números enteros positivos equidistantes aparece en representaciones de series infinitas de varias constantes.

${displaystyle sum _{n=2}^{infty }{bigl (}zeta (n)-1{bigr)}=1}$

De hecho, los términos pares e impares dan las dos sumas

${displaystyle sum _{n=1}^{infty }{bigl (}zeta (2n)-1{bigr)}={frac {3}{4}}}$

${displaystyle sum _{n=1}^{infty }{bigl (}zeta (2n+1)-1{bigr)}={frac {1}{4}}}$

Las versiones parametrizadas de las sumas anteriores están dadas por

${displaystyle sum _{n=1}^{infty }(zeta (2n)-1),t^{2n}={frac {t^{2}}{t^{2}-1}}+{frac {1}{2}}left(1-pi tcot(tpi)right)}$

${displaystyle sum _{n=1}^{infty }(zeta (2n+1)-1),t^{2n}={frac {t^{2}}{t^{2}-1}}-{frac {1}{2}}left(psi ^{0}(t)+psi ^{0}(-t)right)-gamma }$

con $<math alttext="{displaystyle |t|SilenciotSilencio.2{displaystyle Silencioso <img alt="{displaystyle |t|$ y dónde $psi$ y $gamma$ son la función poligamma y la constante de Euler, respectivamente, así como

${displaystyle sum _{n=1}^{infty }{frac {zeta (2n)-1}{n}},t^{2n}=log left({dfrac {1-t^{2}}{operatorname {sinc} (pi ,t)}}right)}$

todos los cuales son continuos $t=1$ . Otras sumas incluyen

${displaystyle sum _{n=2}^{infty }{frac {zeta (n)-1}{n}}=1-gamma }$
${displaystyle sum _{n=2}^{infty }{frac {zeta (n)-1}{n}}left(left({tfrac {3}{2}}right)^{n-1}-1right)={frac {1}{3}}ln pi }$
${displaystyle sum _{n=1}^{infty }{bigl (}zeta (4n)-1{bigr)}={frac {7}{8}}-{frac {pi }{4}}left({frac {e^{2pi }+1}{e^{2pi }-1}}right).}$
${displaystyle sum _{n=2}^{infty }{frac {zeta (n)-1}{n}}operatorname {Im} {bigl (}(1+i)^{n}-(1+i^{n}){bigr)}={frac {pi }{4}}}$

donde In denota la parte imaginaria de un número complejo.

Hay aún más fórmulas en el artículo Número armónico.

Generalizaciones

Existe una serie de funciones zeta relacionadas que pueden considerarse generalizaciones de la función zeta de Riemann. Estos incluyen la función zeta de Hurwitz

$zeta (s,q)=sum _{k=0}^{infty }{frac {1}{(k+q)^{s}}}$

(la representación en serie convergente fue dada por Helmut Hasse en 1930, cf. función zeta de Hurwitz), que coincide con la función zeta de Riemann cuando $q = 1$ (el límite inferior de suma en la función zeta de Hurwitz es 0, no 1), las funciones L de Dirichlet y la función zeta de Dedekind. Para otras funciones relacionadas, consulte los artículos función zeta y función L.

El polilogaritmo está dado por

${displaystyle operatorname {Li} _{s}(z)=sum _{k=1}^{infty }{frac {z^{k}}{k^{s}}}}$

que coincide con la función zeta de Riemann cuando $z = 1$ . La función de Clausen $Cl s (θ)$ se puede elegir como parte real o imaginaria de $Li s (e iθ)$ .

El trascendente de Lerch está dado por

${displaystyle Phi (z,s,q)=sum _{k=0}^{infty }{frac {z^{k}}{(k+q)^{s}}}}$

que coincide con la función zeta de Riemann cuando $z = 1$ y $q = 1$ (el límite inferior de suma en el trascendente de Lerch es 0, no 1).

Las múltiples funciones zeta están definidas por

$k_{2}>cdots >k_{n}>0}{k_{1}}^{-s_{1}}{k_{2}}^{-s_{2}}cdots {k_{n}}^{-s_{n}}.}" xmlns="http://www.w3.org/1998/Math/MathML">Especificaciones Especificaciones ()s1,s2,...... ,sn)=.. k1■k2■⋯ ⋯ ■kn■0k1− − s1k2− − s2⋯ ⋯ kn− − sn.{displaystyle zeta (s_{1},s_{2},ldotss_{n}=sum ################################################################################################################################################################################################################################################################ {fn} {fn}cdots}cdots {k_{n}} {-s_{n}}k_{2}>cdots >k_{n}>0}{k_{1}}^{-s_{1}}{k_{2}}^{-s_{2}}cdots {k_{n}}^{-s_{n}}.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/599ae2f60b54ef2a1bfa8579459ad841d246f0ef" style="vertical-align: -3.338ex; width:52.838ex; height:5.843ex;"/>$

Se pueden continuar analíticamente estas funciones hasta el espacio complejo $n$ -dimensional. Los valores especiales que toman estas funciones en argumentos enteros positivos son llamados valores zeta múltiples por los teóricos de los números y se han relacionado con muchas ramas diferentes de las matemáticas y la física.

Contenido relacionado

Número hipercomplejo
Sociología de las matemáticas
La sociología matemática o la sociología de las matemáticas es un campo de investigación interdisciplinario relacionado tanto con el uso de las...
Alfombra sierpiński
Más resultados...
Te puede interesar