Función W de Lambert

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Función multivalorada en matemáticas

El producto logarithm Lambert W función trazado en el plano complejo desde

-2 - 2 i

2 + 2 i

El gráfico de

Sí. = W () x)

de verdad

x 6

Sí. ■ -4

. La rama superior (azul) con

Sí. \geq -1

es el gráfico de la función

W 0

(Subdivisión principal), la rama inferior (magenta) con

Sí. \leq 1

es el gráfico de la función

W -1

. El valor mínimo x está en {−1/e,1}

En matemáticas, la función Lambert $W$ , también llamada función omega o logaritmo del producto, es una función de varios valores, es decir, las ramas de la relación inversa de la función $f (w) = nosotros w$ , donde $w$ es cualquier número complejo y $e w$ es la función exponencial

Para cada entero $k$ hay una rama, denotada por $W k (z)$ , que es una función de valor complejo de un argumento complejo. $W 0$ se conoce como la rama principal. Estas funciones tienen la siguiente propiedad: si $z$ y $w$ son cualquier número complejo, entonces

{displaystyle we^{w}=z}

se cumple si y solo si

{displaystyle w=W_{k}(z) {text{ for some integer }}k.}

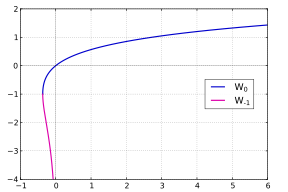
Cuando se trata solo de números reales, las dos ramas $W 0$ y $W -1$ es suficiente: para números reales $x$ y $y$ la ecuación

{displaystyle ye^{y}=x}

puede resolverse para $y$ solo si $x \geq - 1 / e$ ; obtenemos $y = W 0 (x)$ si $x \geq 0$ y los dos valores $y = W 0 (x)$ y $y = W -1 (x)$ si $- 1 / e \leq x < 0$ .

La relación Lambert $W$ no se puede expresar en términos de funciones elementales. Es útil en combinatoria, por ejemplo, en la enumeración de árboles. Se puede usar para resolver varias ecuaciones que involucran exponenciales (por ejemplo, los máximos de las distribuciones de Planck, Bose-Einstein y Fermi-Dirac) y también ocurre en la solución de ecuaciones diferenciales de retardo, como y′(t) = a y(t − 1). En bioquímica, y en cinética enzimática en particular, se describe una solución de forma abierta para el análisis de la cinética del curso del tiempo de la cinética de Michaelis-Menten en términos de Lambert $W$ .

Rama principal del Lambert

W

función en el plano complejo, trazado con coloración de dominio. Nota la rama cortada a lo largo del eje real negativo, terminando en

- 1 / e

El módulo de la rama principal del Lambert

W

función, de color según

arg W () z)

Terminología

La función Lambert $W$ lleva el nombre de Johann Heinrich Lambert. La rama principal $W 0$ se denota $Wp$ en la Biblioteca digital de funciones matemáticas, y la rama $W -1$ se denota $Wm$ allí.

La convención de notación elegida aquí (con $W 0$ y $W -1$ ) sigue la referencia canónica en Lambert $W$ función de Corless, Gonnet, Hare, Jeffrey y Knuth.

El nombre "logaritmo del producto" puede entenderse así: Dado que la función inversa de $f (w) = e w$ se llama logaritmo, tiene sentido llamar a la inversa "función" del producto $nosotros w$ como "logaritmo del producto". (Nota técnica: al igual que el logaritmo complejo, tiene varios valores y, por lo tanto, W se describe como la relación inversa en lugar de la función inversa). Está relacionado con la constante Omega, que es igual a $W 0 (1)$ .

Historia

Lambert consideró por primera vez la ecuación trascendental de Lambert relacionada en 1758, lo que condujo a un artículo de Leonhard Euler en 1783 que analizaba el caso especial de $nosotros w$ .

La ecuación que consideró Lambert fue

{displaystyle x=x^{m}+q.}

Euler transformó esta ecuación en la forma

{displaystyle x^{a}-x^{b}=(a-b)cx^{a+b}.}

Ambos autores derivaron una solución en serie para sus ecuaciones.

Una vez que Euler resolvió esta ecuación, consideró el caso $a = b$ . Tomando límites, derivó la ecuación

{displaystyle ln x=cx^{a}.}

Luego puso $a = 1$ y obtuvo una solución en serie convergente para la ecuación resultante, expresando x en términos de c.

Después de tomar derivadas con respecto a $x$ y algunas manipulaciones, se obtiene la forma estándar de la función de Lambert.

En 1993, se informó que la función $W$ de Lambert proporciona una solución exacta al Dirac de doble pozo de la mecánica cuántica. modelo de función delta para cargas iguales: un problema fundamental en física. Impulsados por esto, Rob Corless y los desarrolladores del sistema de álgebra computacional Maple se dieron cuenta de que "la función W de Lambert ha sido ampliamente utilizada en muchos campos, pero debido a las diferencias de notación y la ausencia de un nombre estándar, el conocimiento de la función era no tan alto como debería haber sido."

Otro ejemplo donde se encuentra esta función es en la cinética de Michaelis-Menten.

Aunque se creía ampliamente que la función Lambert $W$ no se puede expresar en términos de funciones elementales (Liouvillian), la primera la prueba publicada no apareció hasta 2008.

Propiedades elementales, ramas y rango

El rango de la

W

función, mostrando todas las ramas. Las curvas negras (incluyendo el eje real) forman la imagen del eje real, las curvas naranjas son la imagen del eje imaginario. La curva púrpura es la imagen de un pequeño círculo alrededor del punto

z = 0

; las curvas rojas son la imagen de un pequeño círculo alrededor del punto

z = 1 / e

Parcela de la parte imaginaria de W[n,x+i y] para ramas n=-2,-1,0,1,2. La trama es similar a la de la función multivalorada de logaritmo complejo excepto que el espaciado entre hojas no es constante y la conexión de la hoja principal es diferente

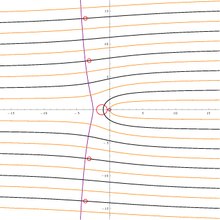
Existen muchas ramas contables de la función $W$ , indicadas por $W k (z)$ , para entero $k; W 0 (z) siendo la rama principal (o principal). W 0 (z) se define para todos los números complejos z mientras que W k (z) con k \neq 0 se define para todos los z distintos de cero. Tenemos W 0 (0) = 0 y lim z \to0 W k (z) = -\infty para todos los k \neq 0 .$

El punto de ramificación para la rama principal está en $z = - 1 / e$ , con un corte de rama que se extiende hasta $-\infty$ a lo largo del eje real negativo. Este corte de rama separa la rama principal de las dos ramas $W -1$ y $W 1$ . En todas las ramas $W k$ con $k \neq 0$ , hay un punto de bifurcación en $z = 0$ y un corte de bifurcación a lo largo de todo el eje real negativo.

Las funciones $W k (z), k \in Z$ son todos inyectivos y sus rangos son disjuntos. El rango de toda la función multivaluada $W$ es el plano complejo. La imagen del eje real es la unión del eje real y la cuadratriz de Hipias, la curva paramétrica $w = - t cot t + it$ .

Inverso

Regiones del plano complejo para el cual

{displaystyle W(n,ze^{z})=z}

, donde z = x + i. Los límites más oscuros de una región particular se incluyen en la región más ligera del mismo color. El punto a {−1, 0} está incluido en ambos

n=-1

(azul) region and the

n=0

Región. Líneas de rejilla horizontales están en múltiples π.

La trama de gama arriba también delinea las regiones en el plano complejo donde la relación inversa simple ${displaystyle W(n,ze^{z})=z}$ es verdad. f=ze^z implica que existe n tales que ${displaystyle z=W(n,f)=W(n,ze^{z})}$ , donde n depende del valor z. El valor del entero n cambios abruptamente cuando ze^z está en la rama cortada ${displaystyle W(n,ze^{z})}$ , lo que significa que $ze z \leq 0$ , excepto para $n=0$ donde está $ze z \leq 1/ e$ .

Definición $z=x+iy$ , donde x y Sí. son reales, y expresar e^z en coordenadas polares, se ve que

{displaystyle {begin{aligned}ze^{z}&=(x+iy)e^{x}(cos y+isin y)\&=e^{x}(xcos y-ysin y)+ie^{x}(xsin y+ycos y).\end{aligned}}}

Para $nneq 0$ , la rama cortada ${displaystyle W(n,ze^{z})}$ es el eje real no positivo, así que

{displaystyle xsin y+ycos y=0Rightarrow x=-y/tan(y),}

{displaystyle (xcos y-ysin y)e^{x}leq 0.}

Para $n=0$ , la rama cortada ${displaystyle W[n,ze^{z}]}$ es el eje real con $<math alttext="{displaystyle -infty - - JUEGO JUEGO .z\leq \leq - - 1/e{displaystyle - 'infty' <img alt="{displaystyle -infty$ , para que la desigualdad se convierta

{displaystyle (xcos y-ysin y)e^{x}leq -1/e.}

Dentro de las regiones atadas por lo anterior, no hay cambios discontinuos en ${displaystyle W(n,ze^{z})}$ , y esas regiones especifican dónde W la función es simplemente invertible, es decir. ${displaystyle W(n,ze^{z})=z}$ .

Cálculo

Derivado

Por diferenciación implícita, se puede mostrar que todas las ramas de $W$ satisfacen la ecuación diferencial

{displaystyle z(1+W){frac {dW}{dz}}=Wquad {text{for }}zneq -{frac {1}{e}}.}

( $W$ no es diferenciable para $z = - 1 / e$ ). Como consecuencia, obtenemos la siguiente fórmula para la derivada de W:

{displaystyle {frac {dW}{dz}}={frac {W(z)}{z(1+W(z))}}quad {text{for }}znot in left{0,-{frac {1}{e}}right}.}

Usando la identidad $e W (z) = z / W (z)$ , obtenemos la siguiente fórmula equivalente:

{displaystyle {frac {dW}{dz}}={frac {1}{z+e^{W(z)}}}quad {text{for }}zneq -{frac {1}{e}}.}

En el origen tenemos

{displaystyle W'_{0}(0)=1.}

Integrales

La función $W (x)$ , y muchas otras expresiones que involucran $W (x)$ , se puede integrar usando la sustitución $w = W (x)$ , es decir, $x = nosotros w$ :

{displaystyle {begin{aligned}int W(x),dx&=xW(x)-x+e^{W(x)}+C\&=xleft(W(x)-1+{frac {1}{W(x)}}right)+C.end{aligned}}}

(La última ecuación es más común en la literatura pero no está definida en $x = 0$ ). Una consecuencia de esto (utilizando el hecho de que $W 0 (e) = 1$ ) es la identidad

{displaystyle int _{0}^{e}W_{0}(x),dx=e-1.}

Expansiones asintóticas

La serie de Taylor de $W 0$ alrededor de 0 se puede encontrar utilizando el teorema de inversión de Lagrange y viene dada por

{displaystyle W_{0}(x)=sum _{n=1}^{infty }{frac {(-n)^{n-1}}{n!}}x^{n}=x-x^{2}+{tfrac {3}{2}}x^{3}-{tfrac {8}{3}}x^{4}+{tfrac {125}{24}}x^{5}-cdots.}

El radio de convergencia es $1 / e$ , como puede verse en la prueba de la razón. La función definida por esta serie se puede extender a una función holomorfa definida en todos los números complejos con una rama cortada a lo largo del intervalo $(-\infty, - 1 / e]$ ; esta función holomorfa define la rama principal de la función Lambert $W$ .

Para valores grandes de $x$ , $W 0$ es asintótico a

{displaystyle {begin{aligned}W_{0}(x)&=L_{1}-L_{2}+{frac {L_{2}}{L_{1}}}+{frac {L_{2}left(-2+L_{2}right)}{2L_{1}^{2}}}+{frac {L_{2}left(6-9L_{2}+2L_{2}^{2}right)}{6L_{1}^{3}}}+{frac {L_{2}left(-12+36L_{2}-22L_{2}^{2}+3L_{2}^{3}right)}{12L_{1}^{4}}}+cdots \[5pt]&=L_{1}-L_{2}+sum _{l=0}^{infty }sum _{m=1}^{infty }{frac {(-1)^{l}left[{begin{smallmatrix}l+m\l+1end{smallmatrix}}right]}{m!}}L_{1}^{-l-m}L_{2}^{m},end{aligned}}}

donde $L 1 = ln x$ , $L 2 = ln ln x$ , y $[l + m l + 1]$ es un número de Stirling no negativo del primer tipo. Manteniendo solo los dos primeros términos de la expansión,

{displaystyle W_{0}(x)=ln x-ln ln x+{mathcal {o}}(1).}

La otra rama real, $W -1$ , definida en el intervalo $[- 1 / e, 0)$ , tiene una aproximación de la misma forma que $x$ tiende a cero, en este caso $L 1 = ln(- x)$ y $L 2 = ln(-ln(- x)).$

Potencias enteras y complejas

Las potencias enteras de $W 0$ también admiten expansiones simples de la serie de Taylor (o Laurent) en cero:

{displaystyle W_{0}(x)^{2}=sum _{n=2}^{infty }{frac {-2left(-nright)^{n-3}}{(n-2)!}}x^{n}=x^{2}-2x^{3}+4x^{4}-{tfrac {25}{3}}x^{5}+18x^{6}-cdots.}

Más generalmente, para $r \in Z$ , la fórmula de inversión de Lagrange da

{displaystyle W_{0}(x)^{r}=sum _{n=r}^{infty }{frac {-rleft(-nright)^{n-r-1}}{(n-r)!}}x^{n},}

que es, en general, una serie de Laurent de orden $r$ . De manera equivalente, este último puede escribirse en forma de desarrollo de potencias de Taylor de $W 0 (x) / x$ :

{displaystyle left({frac {W_{0}(x)}{x}}right)^{r}=e^{-rW_{0}(x)}=sum _{n=0}^{infty }{frac {rleft(n+rright)^{n-1}}{n!}}left(-xright)^{n},}

que se cumple para cualquier $r \in C$ y $| x | < 1 / e$ .

Límites y desigualdades

Se conocen varios límites no asintóticos para la función de Lambert.

Hoorfar y Hassani demostraron que el siguiente límite se cumple para $x \geq e$ :

{displaystyle ln x-ln ln x+{frac {ln ln x}{2ln x}}leq W_{0}(x)leq ln x-ln ln x+{frac {e}{e-1}}{frac {ln ln x}{ln x}}.}

También mostraron el límite general

{displaystyle W_{0}(x)leq log left({frac {x+y}{1+log(y)}}right),}

para todos $1/e}" xmlns="http://www.w3.org/1998/Math/MathML">Sí.■1/e{displaystyle y confiado1/e}1/e}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5da08c735da9c3b908a8e8207f7d13a3c624787b" style="vertical-align: -0.838ex; width:7.662ex; height:2.843ex;"/>$ y ${displaystyle xgeq -1/e}$ , con igualdad sólo para ${displaystyle x=ylog(y)}$ . El límite permite hacer muchos otros límites, como tomar $y=x+1$ que da el límite

{displaystyle W_{0}(x)leq log left({frac {2x+1}{1+log(x+1)}}right).}

En 2013 se demostró que la rama $W -1$ se puede delimitar de la siguiente manera:

<math alttext="{displaystyle -1-{sqrt {2u}}-u<W_{-1}left(-e^{-u-1}right)0.}" xmlns="http://www.w3.org/1998/Math/MathML">− − 1− − 2u− − u.W− − 1()− − e− − u− − 1).− − 1− − 2u− − 23uparau■0.{displaystyle -1-{sqrt {2u}}-ustedW_{-1}left(-e^{-u-1}right) {2}{3}uquad {text{for}} - Sí.<img alt="{displaystyle -1-{sqrt {2u}}-u<W_{-1}left(-e^{-u-1}right)0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4cf2cde487b2f1f1ee7175a456648358e0bb4c69" style="vertical-align: -1.338ex; width:63.086ex; height:3.676ex;"/>

Roberto Iacono y John P. Boyd mejoraron los límites como sigue:

{displaystyle ln left({frac {x}{ln x}}right)-{frac {ln left({frac {x}{ln x}}right)}{1+ln left({frac {x}{ln x}}right)}}ln left(1-{frac {ln ln x}{ln x}}right)leq W_{0}(x)leq ln left({frac {x}{ln x}}right)-ln left(left(1-{frac {ln ln x}{ln x}}right)left(1-{frac {ln left(1-{frac {ln ln x}{ln x}}right)}{1+ln left({frac {x}{ln x}}right)}}right)right).}

Identidades

Una parcela de W_j()x e^xDonde el azul es para j=0 y rojo es para j=1. - La línea diagonal representa los intervalos donde W_j()x e^x)=x

El producto logarithm Lambert W función W 2(z) trazado en el plano complejo de -2-2i a 2+2i

Algunas identidades se derivan de la definición:

{displaystyle {begin{aligned}W_{0}(xe^{x})&=x&{text{for }}x&geq -1,\W_{-1}(xe^{x})&=x&{text{for }}x&leq -1.end{aligned}}}

Tenga en cuenta que, dado que $f (x) = xe x$ no es inyectivo, no siempre sostiene que $W (f (x)) = x$ , al igual que con las funciones trigonométricas inversas. Para $x < 0$ y $x \neq -1$ , la ecuación $xe x = ye y$ tiene dos soluciones reales en $y$ , uno de los cuales es, por supuesto, $y = x$ . Entonces, para $i = 0$ y $x < -1$ , así como para $i = -1$ y $x \in (-1, 0)$ , $y = W i (xe x)$ es la otra solución.

Algunas otras identidades:

{displaystyle {begin{aligned}&W(x)e^{W(x)}=x,quad {text{therefore:}}\[5pt]&e^{W(x)}={frac {x}{W(x)}},qquad e^{-W(x)}={frac {W(x)}{x}},qquad e^{nW(x)}=left({frac {x}{W(x)}}right)^{n}.end{aligned}}}

0.}" xmlns="http://www.w3.org/1998/Math/MathML">In⁡ ⁡ W0()x)=In⁡ ⁡ x− − W0()x)parax■0.{displaystyle ln W_{0}(x)=ln x-W_{0}(x)quad {text{for }x}0}0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1df4e8b60b91680f39b59692181bb02cf9b07334" style="vertical-align: -0.838ex; width:36.622ex; height:2.843ex;"/>

{displaystyle W_{0}left(xln xright)=ln xquad {text{and}}quad e^{W_{0}left(xln xright)}=xquad {text{for }}{frac {1}{e}}leq x.}

<math alttext="{displaystyle W_{-1}left(xln xright)=ln xquad {text{and}}quad e^{W_{-1}left(xln xright)}=xquad {text{for }}0W− − 1()xIn⁡ ⁡ x)=In⁡ ⁡ xyeW− − 1()xIn⁡ ⁡ x)=xpara0.x≤ ≤ 1e.{displaystyle W_{-1}left(xln xright)=ln xquad {text{and}quad e^{W_{-1}left(xln xright)}=xquad {text{for }0Seguido {1} {e}}<img alt="{displaystyle W_{-1}left(xln xright)=ln xquad {text{and}}quad e^{W_{-1}left(xln xright)}=xquad {text{for }}0

0end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">W()x)=In⁡ ⁡ xW()x)parax≥ ≥ − − 1e,W()nxnW()x)n− − 1)=nW()x)paran,x■0{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} }xgeq -{frac {1}{e}},\[5pt] diezmleft({frac {nx^{n}}{Wleft(xright)} {n-1}}}right)=nW(x) Conduciendo {fnx}n,x}end{aligned}}}}}}}}0end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e834c16fb0e25cf530b84a39bdcc0bba7c75d762" style="vertical-align: -6.581ex; margin-bottom: -0.257ex; width:43.945ex; height:14.843ex;"/>

(que se puede extender a otros

n

x

si la rama correcta es elegida).

0.}" xmlns="http://www.w3.org/1998/Math/MathML">W()x)+W()Sí.)=W()xSí.()1W()x)+1W()Sí.)))parax,Sí.■0.{displaystyle W(x)+W(y)=Wleft(xyleft({frac {1}{W(x)}}+{frac {1}{W(y)}right)quad {text{for }x,y título0.}0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a81c1f873a7678c1fa948811300b339935ce0749" style="vertical-align: -2.671ex; width:59.44ex; height:6.343ex;"/>

Sustituyendo $-ln x$ en la definición:

<math alttext="{displaystyle {begin{aligned}W_{0}left(-{frac {ln x}{x}}right)&=-ln x&{text{for }}0&e.end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">W0()− − In⁡ ⁡ xx)=− − In⁡ ⁡ xpara0.x≤ ≤ e,W− − 1()− − In⁡ ⁡ xx)=− − In⁡ ⁡ xparax■e.{displaystyle {begin{aligned}W_{0}left(-{frac {ln} x}{x}}right) Alguien=-ln x sentimiento{text{for }0 correspondíaxleq e,\[5pt]W_{-1}left(-{frac {ln x}{x}right) {ln x}{for }x} {end{aligned}}}}}}}}}}}}}}}<img alt="{displaystyle {begin{aligned}W_{0}left(-{frac {ln x}{x}}right)&=-ln x&{text{for }}0&e.end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/108810da107aa426c8708fe1c3eaa34a2da9575e" style="vertical-align: -6.171ex; width:42.935ex; height:13.509ex;"/>

Con la exponencial iterada de Euler $h (x)$ :

{displaystyle {begin{aligned}h(x)&=e^{-W(-ln x)}\&={frac {W(-ln x)}{-ln x}}quad {text{for }}xneq 1.end{aligned}}}

Valores especiales

Los siguientes son valores especiales de la rama principal:

{displaystyle Wleft(-{frac {pi }{2}}right)={frac {ipi }{2}}.}

{displaystyle Wleft(-{frac {1}{e}}right)=-1.}

{displaystyle Wleft(2ln 2right)=ln 2.}

{displaystyle Wleft(xln xright)=ln x {text{ provided }} xgeqslant 1/eapprox 0.36788.}

{displaystyle W(0)=0.}

{displaystyle W(1)=Omega =left(int _{-infty }^{infty }{frac {dt}{left(e^{t}-tright)^{2}+pi ^{2}}}right)^{-1}-1approx 0.56714329ldots }

(la constante omega).

{displaystyle W(1)=e^{-W(1)}=ln left({frac {1}{W(1)}}right)=-ln W(1).}

{displaystyle W(e)=1.}

{displaystyle Wleft(e^{1+e}right)=e.}

{displaystyle W(-1)approx -0.31813+1.33723i.}

Representaciones

La rama principal de la función de Lambert se puede representar mediante una integral propia, debido a Poisson:

<math alttext="{displaystyle -{frac {pi }{2}}W(-x)=int _{0}^{pi }{frac {sin left({tfrac {3}{2}}tright)-xe^{cos t}sin left({tfrac {5}{2}}t-sin tright)}{1-2xe^{cos t}cos(t-sin t)+x^{2}e^{2cos t}}}sin left({tfrac {1}{2}}tright),dtquad {text{for }}|x|− − π π 2W()− − x)=∫ ∫ 0π π pecado⁡ ⁡ ()32t)− − xe#⁡ ⁡ tpecado⁡ ⁡ ()52t− − pecado⁡ ⁡ t)1− − 2xe#⁡ ⁡ t#⁡ ⁡ ()t− − pecado⁡ ⁡ t)+x2e2#⁡ ⁡ tpecado⁡ ⁡ ()12t)dtparaSilencioxSilencio.1e.{displaystyle {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc} {1} {e}}<img alt="{displaystyle -{frac {pi }{2}}W(-x)=int _{0}^{pi }{frac {sin left({tfrac {3}{2}}tright)-xe^{cos t}sin left({tfrac {5}{2}}t-sin tright)}{1-2xe^{cos t}cos(t-sin t)+x^{2}e^{2cos t}}}sin left({tfrac {1}{2}}tright),dtquad {text{for }}|x|

En el dominio más amplio $- 1 / e \leq x \leq e$ , Mező encontró la representación considerablemente más simple:

{displaystyle W(x)={frac {1}{pi }}operatorname {Re} int _{0}^{pi }ln left({frac {e^{e^{it}}-xe^{-it}}{e^{e^{it}}-xe^{it}}}right),dt.}

Otra representación de la rama principal fue encontrada por el mismo autor y previamente por Kalugin-Jeffrey-Corless:

{displaystyle W(x)={frac {1}{pi }}int _{0}^{pi }log left(1+x{frac {sin t}{t}}e^{tcot t}right)dt.}

La siguiente representación de fracción continua también es válida para la sucursal principal:

{displaystyle W(x)={cfrac {x}{1+{cfrac {x}{1+{cfrac {x}{2+{cfrac {5x}{3+{cfrac {17x}{10+{cfrac {133x}{17+{cfrac {1927x}{190+{cfrac {13582711x}{94423+ddots }}}}}}}}}}}}}}}}.}

Además, si $| W (x) | < 1$ :

{displaystyle W(x)={cfrac {x}{exp {cfrac {x}{exp {cfrac {x}{ddots }}}}}}.}

A su vez, si $| W (x) | > e$ , entonces

{displaystyle W(x)=ln {cfrac {x}{ln {cfrac {x}{ln {cfrac {x}{ddots }}}}}}.}

Otras fórmulas

Integrales definidas

Hay varias fórmulas integrales definidas útiles que involucran la rama principal de la función $W$ , incluidas las siguientes:

{displaystyle {begin{aligned}&int _{0}^{pi }Wleft(2cot ^{2}xright)sec ^{2}x,dx=4{sqrt {pi }}.\[5pt]&int _{0}^{infty }{frac {W(x)}{x{sqrt {x}}}},dx=2{sqrt {2pi }}.\[5pt]&int _{0}^{infty }Wleft({frac {1}{x^{2}}}right),dx={sqrt {2pi }}.end{aligned}}}

La primera identidad se puede encontrar escribiendo la integral de Gauss en coordenadas polares.

La segunda identidad se puede derivar haciendo la sustitución $u = W (x)$ , lo que da

{displaystyle {begin{aligned}x&=ue^{u},\[5pt]{frac {dx}{du}}&=(u+1)e^{u}.end{aligned}}}

Así

{displaystyle {begin{aligned}int _{0}^{infty }{frac {W(x)}{x{sqrt {x}}}},dx&=int _{0}^{infty }{frac {u}{ue^{u}{sqrt {ue^{u}}}}}(u+1)e^{u},du\[5pt]&=int _{0}^{infty }{frac {u+1}{sqrt {ue^{u}}}}du\[5pt]&=int _{0}^{infty }{frac {u+1}{sqrt {u}}}{frac {1}{sqrt {e^{u}}}}du\[5pt]&=int _{0}^{infty }u^{tfrac {1}{2}}e^{-{frac {u}{2}}}du+int _{0}^{infty }u^{-{tfrac {1}{2}}}e^{-{frac {u}{2}}}du\[5pt]&=2int _{0}^{infty }(2w)^{tfrac {1}{2}}e^{-w},dw+2int _{0}^{infty }(2w)^{-{tfrac {1}{2}}}e^{-w},dw&&quad (u=2w)\[5pt]&=2{sqrt {2}}int _{0}^{infty }w^{tfrac {1}{2}}e^{-w},dw+{sqrt {2}}int _{0}^{infty }w^{-{tfrac {1}{2}}}e^{-w},dw\[5pt]&=2{sqrt {2}}cdot Gamma left({tfrac {3}{2}}right)+{sqrt {2}}cdot Gamma left({tfrac {1}{2}}right)\[5pt]&=2{sqrt {2}}left({tfrac {1}{2}}{sqrt {pi }}right)+{sqrt {2}}left({sqrt {pi }}right)\[5pt]&=2{sqrt {2pi }}.end{aligned}}}

La tercera identidad puede derivarse de la segunda haciendo la sustitución $u = x -2$ y el primero también puede derivarse del tercero mediante la sustitución $z = 1 / \sqrt 2 bronceado x$ .

Excepto $z$ a lo largo del corte de rama $(-\infty, - 1 / e]$ (donde la integral no converge), la rama principal de Lambert $W$ se puede calcular mediante la siguiente integral:

{displaystyle {begin{aligned}W(z)&={frac {z}{2pi }}int _{-pi }^{pi }{frac {left(1-nu cot nu right)^{2}+nu ^{2}}{z+nu csc nu e^{-nu cot nu }}},dnu \[5pt]&={frac {z}{pi }}int _{0}^{pi }{frac {left(1-nu cot nu right)^{2}+nu ^{2}}{z+nu csc nu e^{-nu cot nu }}},dnuend{aligned}}}

donde las dos expresiones integrales son equivalentes debido a la simetría del integrando.

Integrales indefinidas

{displaystyle int {frac {W(x)}{x}},dx;=;{frac {W(x)^{2}}{2}}+W(x)+C}

Primera prueba

Introduce substitution variable ${displaystyle u=W(x)rightarrow ue^{u}=x;;;;{frac {d}{du}}ue^{u}=(u+1)e^{u}}$

{displaystyle int {frac {W(x)}{x}},dx;=;int {frac {u}{ue^{u}}}(u+1)e^{u},du}

{displaystyle int {frac {W(x)}{x}},dx;=;int {frac {cancel {color {OliveGreen}{u}}}{{cancel {color {OliveGreen}{u}}}{cancel {color {BrickRed}{e^{u}}}}}}left(u+1right){cancel {color {BrickRed}{e^{u}}}},du}

{displaystyle int {frac {W(x)}{x}},dx;=;int u+1,du}

{displaystyle int {frac {W(x)}{x}},dx;=;{frac {u^{2}}{2}}+u+C}

{displaystyle u=W(x)}

{displaystyle int {frac {W(x)}{x}},dx;=;{frac {W(x)^{2}}{2}}+W(x)+C}

2a prueba

${displaystyle W(x)e^{W(x)}=xrightarrow {frac {W(x)}{x}}=e^{-W(x)}}$

${displaystyle int {frac {W(x)}{x}},dx;=;int e^{-W(x)},dx}$

{displaystyle u=W(x)rightarrow ue^{u}=x;;;;{frac {d}{,du}}ue^{u}=left(u+1right)e^{u}}

${displaystyle int {frac {W(x)}{x}},dx;=;int e^{-u}(u+1)e^{u},du}$

${displaystyle int {frac {W(x)}{x}},dx;=;int {cancel {color {OliveGreen}{e^{-u}}}}left(u+1right){cancel {color {OliveGreen}{e^{u}}}},du}$

${displaystyle int {frac {W(x)}{x}},dx;=;int u+1,du}$

${displaystyle int {frac {W(x)}{x}},dx;=;{frac {u^{2}}{2}}+u+C}$

{displaystyle u=W(x)}

${displaystyle int {frac {W(x)}{x}},dx;=;{frac {W(x)^{2}}{2}}+W(x)+C}$

{displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {Wleft(Ae^{Bx}right)^{2}}{2B}}+{frac {Wleft(Ae^{Bx}right)}{B}}+C}

Prueba

${displaystyle int Wleft(Ae^{Bx}right),dx;=;int Wleft(Ae^{Bx}right),dx}$

{displaystyle u=Bxrightarrow {frac {u}{B}}=x;;;;{frac {d}{du}}{frac {u}{B}}={frac {1}{B}}}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;int Wleft(Ae^{u}right){frac {1}{B}}du}$

{displaystyle v=e^{u}rightarrow ln left(vright)=u;;;;{frac {d}{dv}}ln left(vright)={frac {1}{v}}}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {1}{B}}int {frac {Wleft(Avright)}{v}}dv}$

{displaystyle w=Avrightarrow {frac {w}{A}}=v;;;;{frac {d}{dw}}{frac {w}{A}}={frac {1}{A}}}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {1}{B}}int {frac {{cancel {color {OliveGreen}{A}}}W(w)}{w}}{cancel {color {OliveGreen}{frac {1}{A}}}}dw}$

{displaystyle t=Wleft(wright)rightarrow te^{t}=w;;;;{frac {d}{dt}}te^{t}=left(t+1right)e^{t}}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {1}{B}}int {frac {t}{te^{t}}}left(t+1right)e^{t}dt}$

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {1}{B}}int {frac {cancel {color {OliveGreen}{t}}}{{cancel {color {OliveGreen}{t}}}{cancel {color {BrickRed}{e^{t}}}}}}left(t+1right){cancel {color {BrickRed}{e^{t}}}}dt}$

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {1}{B}}int t+1dt}$

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {t^{2}}{2B}}+{frac {t}{B}}+C}$

{displaystyle t=Wleft(wright)}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {Wleft(wright)^{2}}{2B}}+{frac {Wleft(wright)}{B}}+C}$

{displaystyle w=Av}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {Wleft(Avright)^{2}}{2B}}+{frac {Wleft(Avright)}{B}}+C}$

{displaystyle v=e^{u}}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {Wleft(Ae^{u}right)^{2}}{2B}}+{frac {Wleft(Ae^{u}right)}{B}}+C}$

{displaystyle u=Bx}

${displaystyle int Wleft(Ae^{Bx}right),dx;=;{frac {Wleft(Ae^{Bx}right)^{2}}{2B}}+{frac {Wleft(Ae^{Bx}right)}{B}}+C}$

{displaystyle int {frac {W(x)}{x^{2}}},dx;=;operatorname {Ei} left(-W(x)right)-e^{-W(x)}+C}

Prueba

Introduce substitution variable ${displaystyle u=W(x)}$ , que nos da ${displaystyle ue^{u}=x}$ y ${displaystyle {frac {d}{du}}ue^{u}=left(u+1right)e^{u}}$

${displaystyle {begin{aligned}int {frac {W(x)}{x^{2}}},dx;&=;int {frac {u}{left(ue^{u}right)^{2}}}left(u+1right)e^{u}du\&=;int {frac {u+1}{ue^{u}}}du\&=;int {frac {u}{ue^{u}}}du;+;int {frac {1}{ue^{u}}}du\&=;int e^{-u}du;+;int {frac {e^{-u}}{u}}duend{aligned}}}$

{displaystyle v=-urightarrow -v=u;;;;{frac {d}{dv}}-v=-1}

${displaystyle int {frac {W(x)}{x^{2}}},dx;=;int e^{v}left(-1right)dv;+;int {frac {e^{-u}}{u}}du}$

${displaystyle int {frac {W(x)}{x^{2}}},dx;=;-e^{v}+operatorname {Ei} left(-uright)+C}$

{displaystyle v=-u}

${displaystyle int {frac {W(x)}{x^{2}}},dx;=;-e^{-u}+operatorname {Ei} left(-uright)+C}$

{displaystyle u=W(x)}

${displaystyle {begin{aligned}int {frac {W(x)}{x^{2}}},dx;&=;-e^{-W(x)}+operatorname {Ei} left(-W(x)right)+C\&=;operatorname {Ei} left(-W(x)right)-e^{-W(x)}+Cend{aligned}}}$

Aplicaciones

Resolver ecuaciones

La función Lambert $W$ se utiliza para resolver ecuaciones en las que la cantidad desconocida se encuentra tanto en la base como en el exponente, o tanto dentro como fuera de un logaritmo. La estrategia es convertir dicha ecuación en una de la forma $ze z = w$ y luego para resolver $z$ usando $W$ función.

Por ejemplo, la ecuación

{displaystyle 3^{x}=2x+2}

(donde $x$ es un número real desconocido) puede resolverse reescribiéndolo como

{displaystyle {begin{aligned}&(x+1) 3^{-x}={frac {1}{2}}&({mbox{multiply by }}3^{-x}/2)\Leftrightarrow &(-x-1) 3^{-x-1}=-{frac {1}{6}}&({mbox{multiply by }}{-}1/3)\Leftrightarrow &(ln 3)(-x-1) e^{(ln 3)(-x-1)}=-{frac {ln 3}{6}}&({mbox{multiply by }}ln 3)end{aligned}}}

Esta última ecuación tiene la forma deseada y las soluciones para x reales son:

{displaystyle (ln 3)(-x-1)=W_{0}left({frac {-ln 3}{6}}right) {textrm {or}} (ln 3)(-x-1)=W_{-1}left({frac {-ln 3}{6}}right)}

y así:

{displaystyle x=-1-{frac {W_{0}left(-{frac {ln 3}{6}}right)}{ln 3}}=-0.79011ldots {textrm {or}} x=-1-{frac {W_{-1}left(-{frac {ln 3}{6}}right)}{ln 3}}=1.44456ldots }

Por lo general, la solución a

{displaystyle x=a+b,e^{cx}}

es:

{displaystyle x=a-{frac {1}{c}}W(-bc,e^{ac})}

donde a, b y c son constantes complejas, con b y c no es igual a cero, y la función W es de cualquier orden entero.

Flujos viscosos

Los frentes y depósitos de flujo granular y de escombros, y los frentes de fluidos viscosos en eventos naturales y en experimentos de laboratorio se pueden describir utilizando la función omega de Lambert-Euler de la siguiente manera:

{displaystyle H(x)=1+Wleft((H(0)-1)e^{(H(0)-1)-{frac {x}{L}}}right),}

donde $H (x)$ es la altura del flujo de escombros, $x$ es la posición descendente del canal, $L$ es el parámetro del modelo unificado que consiste de varios parámetros físicos y geométricos del caudal, la altura del caudal y el gradiente de presión hidráulica.

En el flujo de tuberías, la función Lambert W es parte de la formulación explícita de la ecuación de Colebrook para encontrar el factor de fricción de Darcy. Este factor se usa para determinar la caída de presión a través de un tramo recto de tubería cuando el flujo es turbulento.

Flujo dependiente del tiempo en sistemas hidráulicos de derivación simple

La rama principal de la función Lambert $W$ se empleó en el campo de la ingeniería mecánica, en el estudio de la transferencia dependiente del tiempo de fluidos newtonianos entre dos yacimientos con diferentes niveles de superficie libre, utilizando bombas centrífugas. La función $W$ de Lambert proporcionó una solución exacta para el caudal de fluido en los regímenes laminar y turbulento:

{displaystyle {begin{aligned}Q_{text{turb}}&={frac {Q_{i}}{zeta _{i}}}W_{0}left[zeta _{i},e^{(zeta _{i}+beta t/b)}right]\Q_{text{lam}}&={frac {Q_{i}}{xi _{i}}}W_{0}left[xi _{i},e^{left(xi _{i}+beta t/(b-Gamma _{1})right)}right]end{aligned}}}

Q_{i}

t

Neuroimagen

La función Lambert $W$ se empleó en el campo de la neuroimagen para vincular los cambios en el flujo sanguíneo cerebral y el consumo de oxígeno dentro de un vóxel cerebral., a la correspondiente señal dependiente del nivel de oxigenación de la sangre (BOLD).

Ingeniería química

La función $W$ de Lambert se empleó en el campo de la ingeniería química para modelar el espesor de la película del electrodo poroso en una base de carbono vítreo. Supercondensador para almacenamiento de energía electroquímica. La función $W$ de Lambert resultó ser la solución exacta para un proceso de activación térmica en fase gaseosa donde el crecimiento de la película de carbono y la combustión del misma película compiten entre sí.

Crecimiento de cristales

En el crecimiento del cristal, la distribución del soluto se puede obtener utilizando la ecuación Scheil. Así que el principal negativo de la función W de Lambert se puede utilizar para calcular el coeficiente de distribución, ${textstyle k}$ :

${displaystyle {begin{aligned}&k={frac {W(Z)}{ln(1-fs)}}\&Z={frac {C_{S}}{C_{0}}}(1-fs)ln(1-fs)end{aligned}}}$

Ciencia de los materiales

La función $W$ de Lambert se empleó en el campo del crecimiento de la película epitaxial para determinar el espesor de la película de inicio de dislocación crítica. Este es el espesor calculado de una película epitaxial, donde debido a los principios termodinámicos la película desarrollará dislocaciones cristalográficas para minimizar la energía elástica almacenada en las películas. Antes de la aplicación de Lambert $W$ para este problema, el grosor crítico tenía que determinarse resolviendo una ecuación implícita. Lambert $W$ lo convierte en una ecuación explícita para el manejo analítico con facilidad.

Medios porosos

La función Lambert $W$ se ha empleado en el campo del flujo de fluidos en medios porosos para modelar la inclinación de una interfaz que separa dos fluidos segregados gravitacionalmente en un lecho homogéneo poroso inclinado de buzamiento y espesor constante donde el fluido más pesado, inyectado en el extremo inferior, desplaza al fluido más liviano que se produce a la misma velocidad en el extremo superior. La rama principal de la solución corresponde a desplazamientos estables mientras que la rama −1 se aplica si el desplazamiento es inestable con el fluido más pesado corriendo por debajo del fluido más ligero.

Números de Bernoulli y género Todd

La ecuación (vinculada con las funciones generatrices de los números de Bernoulli y el género de Todd):

Y={frac {X}{1-e^{X}}}

puede resolverse mediante las dos ramas reales $W 0$ y $W -1$ :

<math alttext="{displaystyle X(Y)={begin{cases}W_{-1}left(Ye^{Y}right)-W_{0}left(Ye^{Y}right)=Y-W_{0}left(Ye^{Y}right)&{text{for }}Y<-1,\W_{0}left(Ye^{Y}right)-W_{-1}left(Ye^{Y}right)=Y-W_{-1}left(Ye^{Y}right)&{text{for }}-1<YX()Y)={}W− − 1()YeY)− − W0()YeY)=Y− − W0()YeY)paraY.− − 1,W0()YeY)− − W− − 1()YeY)=Y− − W− − 1()YeY)para− − 1.Y.0.{displaystyle X(Y)={begin{cases}W_{-1}left(Ye^{Y}right)-W_{0}left(Ye^{Y}right)=Y-W_{0}left(Ye^{Y}right) }}Y se hizo-1,W_{0}left(Ye^{Y}right)-W_{-1}left(Ye^{Y}right)=Y-W_{-1}left (Ye^{Y}right) - No.<img alt="{displaystyle X(Y)={begin{cases}W_{-1}left(Ye^{Y}right)-W_{0}left(Ye^{Y}right)=Y-W_{0}left(Ye^{Y}right)&{text{for }}Y<-1,\W_{0}left(Ye^{Y}right)-W_{-1}left(Ye^{Y}right)=Y-W_{-1}left(Ye^{Y}right)&{text{for }}-1<Y

Esta aplicación muestra que la diferencia de rama de la función $W$ se puede emplear para resolver otras ecuaciones trascendentales.

Estadísticas

El centroide de un conjunto de histogramas definido con respecto a la divergencia Kullback-Leibler simetrizada (también llamada divergencia de Jeffreys) tiene una forma cerrada usando Lambert $W$ función.

Combinación de pruebas para enfermedades infecciosas

Resolver el tamaño de grupo óptimo para agrupar las pruebas de modo que al menos una persona esté infectada implica la función $W$ de Lambert.

Soluciones exactas de la ecuación de Schrödinger

La función $W$ de Lambert aparece en un potencial mecánico-cuántico, que proporciona la quinta, junto a las del oscilador armónico más centrífugo, el Coulomb más el cuadrado inverso, el Morse y el potencial de la raíz cuadrada inversa: solución exacta de la ecuación de Schrödinger unidimensional estacionaria en términos de las funciones hipergeométricas confluentes. El potencial se da como

{displaystyle V={frac {V_{0}}{1+Wleft(e^{-{frac {x}{sigma }}}right)}}.}

Una peculiaridad de la solución es que cada una de las dos soluciones fundamentales que componen la solución general de la ecuación de Schrödinger viene dada por una combinación de dos funciones hipergeométricas confluentes de argumento proporcional a

{displaystyle z=Wleft(e^{-{frac {x}{sigma }}}right).}

La función Lambert $W$ también aparece en la solución exacta para la energía del estado ligado de la ecuación unidimensional de Schrödinger con un Doble Potencial delta.

Solución exacta de la constante de acoplamiento QCD

En la cromodinámica Cuántica, la teoría del campo cuántico de la interacción Fuerte, la constante de acoplamiento ${displaystyle alpha _{text{s}}}$ se computed perturbatively, el orden n correspondiente a los diagramas Feynman incluyendo n quantum loops. La primera orden, n=1, solución es exacta (en ese orden) y analítica. A órdenes superiores, n título1, no hay una solución exacta y analítica y se utiliza normalmente un método iterativo para proporcionar una solución aproximada. Sin embargo, para el segundo orden, n=2, la función Lambert proporciona una solución exacta (si no analítica).

Soluciones exactas de las ecuaciones del vacío de Einstein

En la solución métrica de Schwarzschild de las ecuaciones de vacío de Einstein, se necesita la función $W$ para pasar de las coordenadas Eddington-Finkelstein a las coordenadas de Schwarzschild. Por ello, también aparece en la construcción de las coordenadas Kruskal-Szekeres.

Resonancias del potencial de capa delta

Las resonancias de onda s del potencial de capa delta se pueden escribir exactamente en términos de la función $W$ de Lambert.

Equilibrio termodinámico

Si una reacción involucra reactivos y productos que tienen capacidades caloríficas que son constantes con la temperatura, entonces la constante de equilibrio $K$ obedece

{displaystyle ln K={frac {a}{T}}+b+cln T}

para algunas constantes $a$ , $b$ y $c$ . Cuando $c$ (igual a $Δ C p / R$ ) no es cero, podemos encontrar el valor o los valores de $T$ donde $K$ es igual a un valor dado de la siguiente manera, donde usamos $L$ para $ln T$ .

{displaystyle {begin{aligned}-a&=(b-ln K)T+cTln T\&=(b-ln K)e^{L}+cLe^{L}\[5pt]-{frac {a}{c}}&=left({frac {b-ln K}{c}}+Lright)e^{L}\[5pt]-{frac {a}{c}}e^{frac {b-ln K}{c}}&=left(L+{frac {b-ln K}{c}}right)e^{L+{frac {b-ln K}{c}}}\[5pt]L&=Wleft(-{frac {a}{c}}e^{frac {b-ln K}{c}}right)+{frac {ln K-b}{c}}\[5pt]T&=exp left(Wleft(-{frac {a}{c}}e^{frac {b-ln K}{c}}right)+{frac {ln K-b}{c}}right).end{aligned}}}

Si $a$ y $c$ tienen el mismo signo habrá dos soluciones o ninguna (o una si el argumento de $W$ es exactamente $- 1 / e$ ). (La solución superior puede no ser relevante). Si tienen signos opuestos, habrá una solución.

Separación de fases de mezclas de polímeros

En el cálculo del diagrama de fase de mezclas de polímeros termodinámicamente incompatibles según el modelo de Edmond-Ogston, las soluciones para binodal y tie-lines se formulan en términos de Lambert $W$ funciones.

La ley de desplazamiento de Wien en un universo D-dimensional

La ley de desplazamiento de Wien se expresa como ${displaystyle nu _{max }/T=alpha =mathrm {const} }$ . Con ${displaystyle x=hnu _{max }/k_{mathrm {B} }T}$ y ${displaystyle drho _{T}left(xright)/dx=0}$ , donde ${displaystyle rho _{T}}$ es la densidad de energía espectral, se encuentra ${displaystyle e^{-x}=1-{frac {x}{D}}}$ . La solución ${displaystyle x=D+Wleft(-De^{-D}right)}$ muestra que la densidad de energía espectral depende de la dimensionalidad del universo.

Correspondencia de AdS/CFT

Las correcciones clásicas de tamaño finito a las relaciones de dispersión de magnones gigantes, picos únicos y cadenas GKP se pueden expresar en términos de Lambert $W función$ .

Epidemiología

En el límite $t \to \infty$ del modelo SIR, la proporción de individuos susceptibles y recuperados tiene solución en términos del Lambert $W$ .

Determinación del tiempo de vuelo de un proyectil

El tiempo total del viaje de un proyectil que experimenta una resistencia del aire proporcional a su velocidad se puede determinar en forma exacta usando el Lambert $W$ función.

Propagación de ondas superficiales electromagnéticas

La ecuación trascendental que aparece en la determinación del número de onda de propagación de una onda superficial axialmente simétrica electromagnética (un modo TM01 único de baja atenuación) que se propaga en un cable metálico cilíndrico da lugar a una ecuación como $u ln u = v$ (donde $u$ y $v$ agrupan los factores geométricos y físicos del problema), que se resuelve mediante la Lambert $W$ función. La primera solución a este problema, debida a Sommerfeld circa 1898, ya contenía un método iterativo para determinar el valor de Lambert $W$ .

Trayectorias ortogonales de elipses reales

La familia de los elipses ${displaystyle x^{2}+(1-varepsilon ^{2})y^{2}=varepsilon ^{2}}$ centrado en $(0,0)$ se parametiza por la excentricidad $varepsilon$ . Las trayectorias ortogonales de esta familia son dadas por la ecuación diferencial ${displaystyle left({frac {1}{y}}+yright)dy=left({frac {1}{x}}-xright)dx}$ cuya solución general es la familia ${displaystyle y^{2}=}$ ${displaystyle W_{0}(x^{2}exp(-2C-x^{2}))}$ .

Generalizaciones

La función estándar de Lambert $W$ expresa soluciones exactas a ecuaciones algebraicas trascendentales (en $x$ ) de la forma:

{displaystyle e^{-cx}=a_{0}(x-r)}

()1)

donde $a 0$ , $c$ y $r$ son constantes reales. La solucion es

{displaystyle x=r+{frac {1}{c}}Wleft({frac {c,e^{-cr}}{a_{0}}}right).}

W

Una aplicación a la relatividad general y la mecánica cuántica (gravedad cuántica) en dimensiones inferiores, de hecho un enlace (no conocido antes de 2007) entre estas dos áreas, donde el lado derecho de (1) es reemplazado por un polinomio cuadrático en x:
${displaystyle e^{-cx}=a_{0}left(x-r_{1}right)left(x-r_{2}right),}$
()2)
Donde $r 1$ y $r 2$ son verdaderas constantes distintas, las raíces del polinomio cuadrático. Aquí, la solución es una función que tiene un solo argumento $x$ pero los términos como $r i$ y $a 0$ son parámetros de esa función. En este sentido, la generalización se asemeja a la función hipergeométrica y a la función Meijer G, pero pertenece a una función diferente clase de funciones. Cuando $r 1 = r 2$ , ambos lados de (2) se puede considerar y reducir a (1) y por lo tanto la solución reduce a la de la norma $W$ función. Ecuación2) expresa la ecuación que rige el campo dilatón, del cual se deriva la métrica de la R = T o lineal problema de gravedad de dos cuerpos en 1 + 1 dimensiones (una dimensión espacial y una dimensión de tiempo) para el caso de masas de reposo desiguales, así como las eigenenergies del modelo de función Dirac delta de doble hilera cuántica desigual cargas en una dimensión.
Soluciones analíticas de las eigenenergies de un caso especial del problema de tres cuerpos mecánicos cuánticos, a saber, la molécula de hidrógeno (tres dimensiones). Aquí el lado derecho de (1) es reemplazado por una proporción de polinomios de orden infinito en $x$ :
${displaystyle e^{-cx}=a_{0}{frac {displaystyle prod _{i=1}^{infty }(x-r_{i})}{displaystyle prod _{i=1}^{infty }(x-s_{i})}}}$
()3)
Donde $r i$ y $s i$ son distintas constantes reales y $x$ es una función de la eigenenergia y la distancia internuclear $R$ . Ecuación3) con sus casos especializados expresados en (1) y (2) está relacionado con una gran clase de ecuaciones diferenciales de demora. G. H. Hardy's notion of a "false derivative" proporciona múltiples raíces exactas a casos especiales de (3).

Las aplicaciones de la función Lambert $W$ en problemas físicos fundamentales no están agotadas ni siquiera para el caso estándar expresado en ( 1) como se ha visto recientemente en el área de la física atómica, molecular y óptica.

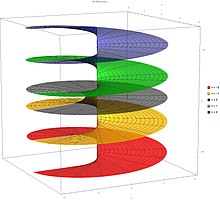
Parcelas

Parcelas del Lambert $W$ función en el plano complejo
$z = Re(W 0 () x + i)$
$z = Im(W 0 () x + i)$
$z = Silencio W 0 () x + i) Silencio$
Superimposición de las tres parcelas anteriores

Evaluación numérica

La función $W$ puede aproximarse usando el método de Newton, con aproximaciones sucesivas a $w = W (z)$ (entonces $z = nosotros w$ ) siendo

w_{j+1}=w_{j}-{frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}+w_{j}e^{w_{j}}}}.

La función $W$ también se puede aproximar usando el método de Halley,

{displaystyle w_{j+1}=w_{j}-{frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}left(w_{j}+1right)-{dfrac {left(w_{j}+2right)left(w_{j}e^{w_{j}}-zright)}{2w_{j}+2}}}}}

dado en Corless et al. para calcular $W$ .

De verdad ${displaystyle xgeq -1/e}$ , podría ser aproximado por la fórmula recursiva de tipo cuadrático de R. Iacono y J.P. Boyd:

{displaystyle w_{n+1}(x)={frac {w_{n}(x)}{1+w_{n}(x)}}left(1+log left({frac {x}{w_{n}(x)}}right)right).}

Lajos Lóczi demuestra que al elegir apropiado ${displaystyle w_{0}(x)}$ ,

si ${displaystyle xin (e,infty)}$ : ${displaystyle w_{0}(x)=log(x)-log(log(x)),}$
si ${displaystyle xin (0,e):}$ ${displaystyle w_{0}(x)=x/e,}$
si x▪ ▪ ()− − 1/e,0):{displaystyle xin (-1/e,0):} ${displaystyle xin (-1/e,0):}$
- para la rama principal $W_{0}$ : ${displaystyle w_{0}(x)={frac {ex}{1+ex+{sqrt {1+ex}}}}log(1+{sqrt {1+ex}}),}$
- para la rama W− − 1{displaystyle W_{-1} $W_{-1}$ :
  - ${displaystyle w_{0}(x)=-1-{sqrt {2(1+ex)}},}$ para ${displaystyle xin (-1/e,-1/4],}$
  - ${displaystyle w_{0}(x)=log(-x)-log(-log(-x)),}$ para ${displaystyle xin (-1/4,0),}$

se puede determinar el número máximo de pasos de iteración por adelantado para cualquier precisión:

si ${displaystyle xin (e,infty)}$ (Teorema 2.4): $<math alttext="{displaystyle 0<W_{0}(x)-w_{n}(x)0.W0()x)− − wn()x).()log⁡ ⁡ ()1+1/e))2n,{displaystyle 0 realizadasW_{0}(x)-w_{n}(x)traducido(log(1+1/e)right)^{2^{n}}}<img alt="{displaystyle 0<W_{0}(x)-w_{n}(x)$
si ${displaystyle xin (0,e)}$ (Teorema 2.9): $<math alttext="{displaystyle 0<W_{0}(x)-w_{n}(x)0.W0()x)− − wn()x).()1− − 1/e)2n− − 15,{displaystyle 0 realizadasW_{0}(x)-w_{n}(x)se hizo {frac {left(1-1/eright)}{2^{n}{5}}}<img alt="{displaystyle 0<W_{0}(x)-w_{n}(x)$
si x▪ ▪ ()− − 1/e,0):{displaystyle xin (-1/e,0):} ${displaystyle xin (-1/e,0):}$
- para la rama principal $W_{0}$ (Teorema 2.17): $<math alttext="{displaystyle 0<w_{n}(x)-W_{0}(x)0.wn()x)− − W0()x).()1/10)2n,{displaystyle 0 madew_{n}(x)-W_{0}(x)tratadoleft(1/10right)^{2^{n} }<img alt="{displaystyle 0<w_{n}(x)-W_{0}(x)$
- para la rama $W_{-1}$ (Teorema 2.23): $<math alttext="{displaystyle 0<W_{-1}(x)-w_{n}(x)0.W− − 1()x)− − wn()x).()1/2)2n.{displaystyle 0 0 0 0 0 0 0 0}(x)-w_{n}(x) 0(1/2right)^{2^{n}<img alt="{displaystyle 0<W_{-1}(x)-w_{n}(x)$

Software

La función Lambert $W$ se implementa como LambertW en Maple, lambertw en GP (y glambertW en PARI), lambertw en Matlab, también lambertw en Octave con specfun paquete, como lambert_w en Maxima, como ProductLog (con un alias silencioso LambertW) en Mathematica, como lambertw en Paquete de funciones especiales de Python scipy, como LambertW en el módulo ntheory de Perl, y como gsl_sf_lambert_W0, gsl_sf_lambert_Wm1 funciona en la sección de funciones especiales de la Biblioteca Científica GNU (GSL). En las bibliotecas de Boost C++, las llamadas son lambert_w0, lambert_wm1, lambert_w0_prime y lambert_wm1_prime. En R, la función Lambert $W$ se implementa como lambertW0 y lambertWm1 funciones en el paquete lamW.

El código C++ para todas las ramas de la compleja función Lambert $W$ está disponible en la página de inicio de István Mező.

Contenido relacionado

Más resultados...