Función totient de Euler

Compartir Imprimir Citar

Número de enteros coprime a y no superior

Los primeros mil valores de

φ () n)

. Los puntos en la línea superior representan

φ () p)

cuando

p

es un número primo, que es

p - 1.

En teoría de números, Función totiente de Euler cuenta los enteros positivos hasta un entero dado $n$ que son relativamente primos $n$ . Está escrito usando la letra griega phi como $varphi (n)$ o $phi (n)$ , y también se puede llamar Función de Euler. En otras palabras, es el número de enteros $k$ en el rango $1 \leq k \leq n$ para el cual el mayor divisor común $gcd(n, k)$ es igual a 1. Los enteros $k$ de esta forma son a veces referidos como totantes de $n$ .

Por ejemplo, los totales de $n = 9$ son los seis números 1, 2, 4, 5, 7 y 8. Todos son relativamente primo a 9, pero los otros tres números en este rango, 3, 6 y 9 no lo son, ya que $mcd(9, 3) = mcd(9, 6) = 3$ y $mcd(9, 9) = 9$ . Por lo tanto, $φ (9) = 6$ . Como otro ejemplo, $φ (1) = 1$ ya que para $n = 1$ el único número entero en el rango de 1 a $n$ es 1 en sí mismo, y $gcd (1, 1) = 1$ .

La función totiente de Euler es una función multiplicativa, lo que significa que si dos números $m$ y $n$ son relativamente primos, entonces $φ () mn) φ () m) φ () n)$ . Esta función da el orden del grupo multiplicador de enteros modulo n (el grupo de unidades del anillo ${displaystyle mathbb {Z} /nmathbb {Z} }$ ). También se utiliza para definir el sistema de encriptación RSA.

Historia, terminología y notación

Leonhard Euler introdujo la función en 1763. Sin embargo, en ese momento no eligió ningún símbolo específico para indicarla. En una publicación de 1784, Euler estudió más la función, eligiendo la letra griega $π$ para denotarla: escribió $πD$ para "la multitud de números menores que $D$ , y que no tienen ningún divisor común con él". Esta definición varía de la definición actual de la función totient en $D = 1$ pero, por lo demás, es la misma. La notación ahora estándar $φ (A)$ proviene del tratado de Gauss de 1801 Disquisitiones Arithmeticae, aunque Gauss no usó paréntesis alrededor del argumento y escribió $φA$ . Por lo tanto, a menudo se la llama función phi de Euler o simplemente la función phi.

En 1879, J. J. Sylvester acuñó el término totient para esta función, por lo que también se la conoce como función totient de Euler, la función de Euler totient, o totient de Euler. El totient de Jordan es una generalización del de Euler.

El cotociente de $n$ se define como $n - φ (n)$ . Cuenta el número de enteros positivos menores o iguales a $n$ que tienen al menos un factor primo en común con n.

Calculando la función totient de Euler

Hay varias fórmulas para calcular $φ (n)$ .

Fórmula del producto de Euler

Establece

{displaystyle varphi (n)=nprod _{pmid n}left(1-{frac {1}{p}}right),}

donde el producto está sobre los distintos números primos que dividen $n$ . (Para notación, consulte Función aritmética).

Una formulación equivalente ${displaystyle n=p_{1}^{k_{1}}p_{2}^{k_{2}}cdots p_{r}^{k_{r}}}$ , donde ${displaystyle p_{1},p_{2},ldotsp_{r}}$ son los principios diferenciados dividir n, es:

{displaystyle varphi (n)=p_{1}^{k_{1}-1}(p_{1}{-}1),p_{2}^{k_{2}-1}(p_{2}{-}1)cdots p_{r}^{k_{r}-1}(p_{r}{-}1).}

Phi es una función multiplicativa

Esto significa que si $gcd(m, n) = 1$ , entonces $φ (m) φ (n) = φ (mn)$ . Esquema de prueba: Sea $A$ , $B$ , $C$ sean los conjuntos de enteros positivos que son coprimos y menores que $m$ , $n$ , $mn$ , respectivamente, de modo que $| A | = φ (m)$ , etc. Entonces hay una biyección entre $A \times B$ y $C$ por el teorema del resto chino.

Valor de phi para un argumento de potencia prima

Si $p$ es primo y $k \geq 1$ , entonces

{displaystyle varphi left(p^{k}right)=p^{k}-p^{k-1}=p^{k-1}(p-1)=p^{k}left(1-{tfrac {1}{p}}right).}

Prueba: dado que $p$ es un número primo, los únicos valores posibles de $gcd(p k, m)$ son $1, p, p 2,..., p k$ , y la única forma de tener $gcd(p k, m) > 1$ es si $m$ es múltiplo de $p$ , es decir, $m \in {p, 2 p, 3 p,..., p k - 1 p = p k}$ , y hay $p k - 1$ dichos múltiplos no mayores que $p k$ . Por lo tanto, el otro $p k - p k - 1$ los números son todos relativamente primos a $p k$ .

Prueba de la fórmula del producto de Euler

El teorema fundamental de la aritmética declara que si $n ■ 1$ hay una expresión única ${displaystyle n=p_{1}^{k_{1}}p_{2}^{k_{2}}cdots p_{r}^{k_{r}},}$ Donde $p 1 . p 2 - No. p r$ son números primos y cada uno $k i \geq 1$ . (El caso $n = 1$ corresponde al producto vacío.) Repetidamente utilizando la propiedad multiplicativa de $φ$ y la fórmula para $φ () p k)$ da

{displaystyle {begin{array}{rcl}varphi (n)&=&varphi (p_{1}^{k_{1}}),varphi (p_{2}^{k_{2}})cdots varphi (p_{r}^{k_{r}})\[.1em]&=&p_{1}^{k_{1}-1}(p_{1}-1),p_{2}^{k_{2}-1}(p_{2}-1)cdots p_{r}^{k_{r}-1}(p_{r}-1)\[.1em]&=&p_{1}^{k_{1}}left(1-{frac {1}{p_{1}}}right)p_{2}^{k_{2}}left(1-{frac {1}{p_{2}}}right)cdots p_{r}^{k_{r}}left(1-{frac {1}{p_{r}}}right)\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}cdots p_{r}^{k_{r}}left(1-{frac {1}{p_{1}}}right)left(1-{frac {1}{p_{2}}}right)cdots left(1-{frac {1}{p_{r}}}right)\[.1em]&=&nleft(1-{frac {1}{p_{1}}}right)left(1-{frac {1}{p_{2}}}right)cdots left(1-{frac {1}{p_{r}}}right).end{array}}}

Esto proporciona ambas versiones de la fórmula del producto de Euler.

Una prueba alternativa que no requiere la propiedad multiplicativa en lugar de utilizar el principio de inclusión-exclusión aplicado al conjunto ${1,2,ldotsn}$ , excluyendo los conjuntos de enteros divisibles por los divisores principales.

Ejemplo

{displaystyle varphi (20)=varphi (2^{2}5)=20,(1-{tfrac {1}{2}}),(1-{tfrac {1}{5}})=20cdot {tfrac {1}{2}}cdot {tfrac {4}{5}}=8.}

En palabras: los distintos factores primos de 20 son 2 y 5; la mitad de los veinte enteros del 1 al 20 son divisibles por 2, quedando diez; una quinta parte de ellos son divisibles por 5, dejando ocho números coprimos con 20; estos son: 1, 3, 7, 9, 11, 13, 17, 19.

La fórmula alternativa usa solo números enteros:

{displaystyle varphi (20)=varphi (2^{2}5^{1})=2^{2-1}(2{-}1),5^{1-1}(5{-}1)=2cdot 1cdot 1cdot 4=8.}

Transformada de Fourier

El tociente es la transformada discreta de Fourier del gcd, evaluada en 1. Sea

{displaystyle {mathcal {F}}{mathbf {x} }[m]=sum limits _{k=1}^{n}x_{k}cdot e^{{-2pi i}{frac {mk}{n}}}}

donde $x k = mcd(k, n)$ para $k \in {1,..., n}$ . Después

{displaystyle varphi (n)={mathcal {F}}{mathbf {x} }[1]=sum limits _{k=1}^{n}gcd(k,n)e^{-2pi i{frac {k}{n}}}.}

La parte real de esta fórmula es

{displaystyle varphi (n)=sum limits _{k=1}^{n}gcd(k,n)cos {tfrac {2pi k}{n}}.}

Por ejemplo, usando ${displaystyle cos {tfrac {pi }{5}}={tfrac {{sqrt {5}}+1}{4}}}$ y ${displaystyle cos {tfrac {2pi }{5}}={tfrac {{sqrt {5}}-1}{4}}}$ :

{displaystyle {begin{array}{rcl}varphi (10)&=&gcd(1,10)cos {tfrac {2pi }{10}}+gcd(2,10)cos {tfrac {4pi }{10}}+gcd(3,10)cos {tfrac {6pi }{10}}+cdots +gcd(10,10)cos {tfrac {20pi }{10}}\&=&1cdot ({tfrac {{sqrt {5}}+1}{4}})+2cdot ({tfrac {{sqrt {5}}-1}{4}})+1cdot (-{tfrac {{sqrt {5}}-1}{4}})+2cdot (-{tfrac {{sqrt {5}}+1}{4}})+5cdot (-1)\&&+ 2cdot (-{tfrac {{sqrt {5}}+1}{4}})+1cdot (-{tfrac {{sqrt {5}}-1}{4}})+2cdot ({tfrac {{sqrt {5}}-1}{4}})+1cdot ({tfrac {{sqrt {5}}+1}{4}})+10cdot (1)\&=&4.end{array}}}

n

n

n

Divisor suma

La propiedad establecida por Gauss, que

{displaystyle sum _{dmid n}varphi (d)=n,}

donde la suma es sobre todos los divisores positivos $d$ de $n$ , se puede probar de varias formas. (Consulte Función aritmética para conocer las convenciones de notación).

Una prueba es notar que $φ (d)$ también es igual al número de posibles generadores del grupo cíclico $C d$ ; específicamente, si $C d = ⟨ g ⟩$ con $g d = 1$ , luego $g k$ es un generador para cada $k$ coprime a $d$ . Dado que cada elemento de $C n$ genera un subgrupo cíclico, y todos los subgrupos $C d \subseteq C n$ son generados precisamente por $φ (d)$ elementos de $C n$ , la fórmula es la siguiente. De manera equivalente, la fórmula se puede derivar mediante el mismo argumento aplicado al grupo multiplicativo de las $n$ ésimas raíces de la unidad y la primitiva $d$ th raíces de unidad.

La fórmula también se puede derivar de la aritmética elemental. Por ejemplo, sea $n = 20$ y considere las fracciones positivas hasta 1 con denominador 20:

{displaystyle {tfrac {1}{20}},,{tfrac {2}{20}},,{tfrac {3}{20}},,{tfrac {4}{20}},,{tfrac {5}{20}},,{tfrac {6}{20}},,{tfrac {7}{20}},,{tfrac {8}{20}},,{tfrac {9}{20}},,{tfrac {10}{20}},,{tfrac {11}{20}},,{tfrac {12}{20}},,{tfrac {13}{20}},,{tfrac {14}{20}},,{tfrac {15}{20}},,{tfrac {16}{20}},,{tfrac {17}{20}},,{tfrac {18}{20}},,{tfrac {19}{20}},,{tfrac {20}{20}}.}

Póngalos en términos mínimos:

{displaystyle {tfrac {1}{20}},,{tfrac {1}{10}},,{tfrac {3}{20}},,{tfrac {1}{5}},,{tfrac {1}{4}},,{tfrac {3}{10}},,{tfrac {7}{20}},,{tfrac {2}{5}},,{tfrac {9}{20}},,{tfrac {1}{2}},,{tfrac {11}{20}},,{tfrac {3}{5}},,{tfrac {13}{20}},,{tfrac {7}{10}},,{tfrac {3}{4}},,{tfrac {4}{5}},,{tfrac {17}{20}},,{tfrac {9}{10}},,{tfrac {19}{20}},,{tfrac {1}{1}}}

Estas veinte fracciones son todas las k/d ≤ 1 cuyos denominadores son los divisores $d = 1, 2, 4, 5, 10, 20$ . Las fracciones con 20 como denominador son aquellas con numeradores relativamente primos a 20, a saber, 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/ 20; por definición, esto es $φ (20)$ fracciones. De manera similar, hay fracciones $φ (10)$ con denominador 10, y $φ (5)$ fracciones con denominador 5, etc. Así, el conjunto de veinte fracciones se divide en subconjuntos de tamaño $φ (d)$ para cada $d$ que divide 20. Se aplica un argumento similar para cualquier n.

La inversión de Möbius aplicada a la fórmula de la suma del divisor da

{displaystyle varphi (n)=sum _{dmid n}mu left(dright)cdot {frac {n}{d}}=nsum _{dmid n}{frac {mu (d)}{d}},}

Donde $μ$ es la función Möbius, la función multiplicativa definida por ${displaystyle mu (p)=-1}$ y ${displaystyle mu (p^{k})=0}$ para cada primo $p$ y $k \geq 2$ . Esta fórmula también puede derivarse de la fórmula del producto multiplicando ${textstyle prod _{pmid n}(1-{frac {1}{p}})}$ para llegar ${textstyle sum _{dmid n}{frac {mu (d)}{d}}.}$

Un ejemplo:

{displaystyle {begin{aligned}varphi (20)&=mu (1)cdot 20+mu (2)cdot 10+mu (4)cdot 5+mu (5)cdot 4+mu (10)cdot 2+mu (20)cdot 1\[.5em]&=1cdot 20-1cdot 10+0cdot 5-1cdot 4+1cdot 2+0cdot 1=8.end{aligned}}}

Algunos valores

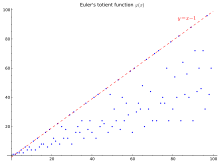
Los primeros 100 valores (secuencia A000010 en el OEIS) se muestran en la tabla y el gráfico a continuación:

Gráfico de los primeros 100 valores

$φ () n)$ para $1 \leq n \leq 100$
+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

En el gráfico a la derecha la línea superior $Sí. = n - 1$ es un límite superior válido para todos $n$ más que uno, y alcanzado si y sólo si $n$ es un número primo. Un simple límite inferior ${displaystyle varphi (n)geq {sqrt {n/2}}}$ , que es bastante flojo: de hecho, el límite inferior del gráfico es proporcional a $n / log n$ .

Teorema de Euler

Esto establece que si $a$ y $n$ son relativamente primos entonces

a^{{varphi (n)}}equiv 1mod n.

El caso especial donde $n$ es primo se conoce como el pequeño teorema de Fermat.

Esto se deriva del teorema de Lagrange y del hecho de que $φ (n)$ es el orden de el grupo multiplicativo de números enteros módulo n.

El criptosistema RSA se basa en este teorema: implica que la inversa de la función $a \mapsto a e mod n$ , donde $e$ es el exponente de cifrado (público), es la función $b \mapsto b d mod n$ , donde $d$ , el exponente de descifrado (privado), es el inverso multiplicativo de $e$ módulo $φ (n)$ . La dificultad de calcular $φ (n)$ sin conocer la factorización de $n$ es, por lo tanto, la dificultad de calcular $d$ : esto se conoce como RSA problema que puede resolverse factorizando $n$ . El propietario de la clave privada conoce la factorización, ya que una clave privada RSA se construye eligiendo $n$ como el producto de dos (aleatoriamente elegido) primos grandes $p$ y $q. Solo n se divulga públicamente y, dada la dificultad de factorizar números grandes, tenemos la garantía de que nadie más conoce la factorización.$

Otras fórmulas

${displaystyle amid bimplies varphi (a)mid varphi (b)}$
${displaystyle mmid varphi (a^{m}-1)}$
φ φ ()mn)=φ φ ()m)φ φ ()n)⋅ ⋅ dφ φ ()d)Donded=gcd⁡ ⁡ ()m,n){displaystyle varphi (mn)=varphi (m)varphi (n)cdot {frac {d}{varphi (d)}quad {text{where ##d=operatorname {gcd} (m,n)} ${displaystyle varphi (mn)=varphi (m)varphi (n)cdot {frac {d}{varphi (d)}}quad {text{where }}d=operatorname {gcd} (m,n)}$
En particular:
- ${displaystyle varphi (2m)={begin{cases}2varphi (m)&{text{ if }}m{text{ is even}}\varphi (m)&{text{ if }}m{text{ is odd}}end{cases}}}$
- ${displaystyle varphi left(n^{m}right)=n^{m-1}varphi (n)}$
${displaystyle varphi (operatorname {lcm} (m,n))cdot varphi (operatorname {gcd} (m,n))=varphi (m)cdot varphi (n)}$
Compare esto con la fórmula ${textstyle operatorname {lcm} (m,n)cdot operatorname {gcd} (m,n)=mcdot n}$ (ver mínimo común múltiple).
$φ () n)$ es incluso para $n \geq 3$ .
Además, si $n$ tiene $r$ diferencia de factores principales, $2 r Silencio φ () n)$
Para cualquier $a ■ 1$ y $n ■ 6$ tales que $4 ∤ n$ existe $l \geq 2 n$ tales que $l Silencio φ () a n -1)$ .
${displaystyle {frac {varphi (n)}{n}}={frac {varphi (operatorname {rad} (n))}{operatorname {rad} (n)}}}$
Donde $rad(n)$ es el radical de n (el producto de todas las primas diferenciadas dividiendo $n$ ).
$sum _{dmid n}{frac {mu ^{2}(d)}{varphi (d)}}={frac {n}{varphi (n)}}$
$1}" xmlns="http://www.w3.org/1998/Math/MathML">.. 1≤ ≤ k≤ ≤ n()k,n)=1k=12nφ φ ()n)paran■1{displaystyle sum _{1leq kleq n atop (k,n)=1}! k={tfrac {1} {2}nvarphi (n)quad {text{for } {fn}nvarphi (n)quad {text{for } {f}nf}nfn]}nvarphi (n)quad {fn]fnf}fnfn4}nf}nfnf}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnf}fnfnf}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/72a45e69403e21c4d701a9d2335565f888249cef" style="vertical-align: -4.838ex; width:28.213ex; height:7.343ex;"/>$
${displaystyle sum _{k=1}^{n}varphi (k)={tfrac {1}{2}}left(1+sum _{k=1}^{n}mu (k)leftlfloor {frac {n}{k}}rightrfloor ^{2}right)={frac {3}{pi ^{2}}}n^{2}+Oleft(n(log n)^{frac {2}{3}}(log log n)^{frac {4}{3}}right)}$ (citado en)
${displaystyle sum _{k=1}^{n}{frac {varphi (k)}{k}}=sum _{k=1}^{n}{frac {mu (k)}{k}}leftlfloor {frac {n}{k}}rightrfloor ={frac {6}{pi ^{2}}}n+Oleft((log n)^{frac {2}{3}}(log log n)^{frac {4}{3}}right)}$
${displaystyle sum _{k=1}^{n}{frac {k}{varphi (k)}}={frac {315,zeta (3)}{2pi ^{4}}}n-{frac {log n}{2}}+Oleft((log n)^{frac {2}{3}}right)}$
${displaystyle sum _{k=1}^{n}{frac {1}{varphi (k)}}={frac {315,zeta (3)}{2pi ^{4}}}left(log n+gamma -sum _{p{text{ prime}}}{frac {log p}{p^{2}-p+1}}right)+Oleft({frac {(log n)^{frac {2}{3}}}{n}}right)}$
(donde) $γ$ es la constante Euler-Mascheroni).
${displaystyle sum _{stackrel {1leq kleq n}{operatorname {gcd} (k,m)=1}}!!!!1=n{frac {varphi (m)}{m}}+Oleft(2^{omega (m)}right)}$
Donde $m ■ 1$ es un entero positivo y $\cdot () m)$ es el número de factores principales distintos $m$ .

Identidad de Menon

En 1965, P. Kesava Menon demostró

{displaystyle sum _{stackrel {1leq kleq n}{gcd(k,n)=1}}!!!!gcd(k-1,n)=varphi (n)d(n),}

donde $d(n) = σ0(n)$ es el número de divisores de $n$ .

Funciones generadoras

La serie de Dirichlet para $φ (n)$ puede escribirse en términos de la función zeta de Riemann como:

sum _{{n=1}}^{infty }{frac {varphi (n)}{n^{s}}}={frac {zeta (s-1)}{zeta (s)}}

donde converge el lado izquierdo $2}" xmlns="http://www.w3.org/1998/Math/MathML">R R ()s)■2{displaystyle Re (s)2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f75c84c17f43158d1f7fc4c3e8ece0e0bb3f8140" style="vertical-align: -0.838ex; width:9.085ex; height:2.843ex;"/>$ .

La función generadora de la serie de Lambert es

sum _{n=1}^{infty }{frac {varphi (n)q^{n}}{1-q^{n}}}={frac {q}{(1-q)^{2}}}

que converge para $| q | < 1$ .

Ambos se prueban mediante manipulaciones de series elementales y las fórmulas para $φ (n)$ .

Tasa de crecimiento

En palabras de Hardy & Wright, el orden de $φ (n)$ es "siempre 'casi n'."

Primero

{displaystyle lim sup {frac {varphi (n)}{n}}=1,}

pero como n tiende a infinito, para todo $δ > 0$

{displaystyle {frac {varphi (n)}{n^{1-delta }}}rightarrow infty.}

Estas dos fórmulas se pueden probar usando poco más que las fórmulas para $φ (n)$ y el divisor función de suma $σ (n)$ .

De hecho, durante la demostración de la segunda fórmula, la desigualdad

<math alttext="{displaystyle {frac {6}{pi ^{2}}}<{frac {varphi (n)sigma (n)}{n^{2}}}6π π 2.φ φ ()n)σ σ ()n)n2.1,{displaystyle {frac {6}{2}} {frac {varphi (n)sigma (n)}{n^{2}}} {}}} {c}}}} {c}}}}} {c}}}}}}} {f}}}}}} {f}}}}}}}}} {<img alt="{displaystyle {frac {6}{pi ^{2}}}<{frac {varphi (n)sigma (n)}{n^{2}}}

verdadero para $n > 1$ , está probado.

También tenemos

{displaystyle lim inf {frac {varphi (n)}{n}}log log n=e^{-gamma }.}

Aquí $γ$ es la constante de Euler, $γ = 0,577215665...$ , entonces $e γ = 1,7810724...$ y $e - γ = 0,56145948...$ .

Demostrar esto no requiere del todo el teorema de los números primos. Dado que $log log n$ tiende a infinito, esta fórmula muestra que

{displaystyle lim inf {frac {varphi (n)}{n}}=0.}

De hecho, más es verdad.

{frac {n}{e^{gamma };log log n+{frac {3}{log log n}}}}quad {text{for }}n>2}" xmlns="http://www.w3.org/1998/Math/MathML">φ φ ()n)■neγ γ log⁡ ⁡ log⁡ ⁡ n+3log⁡ ⁡ log⁡ ⁡ nparan■2{displaystyle varphi (n) confianza{frac {n}{e^{gamma };log log n+{frac {3} {logloglog}}}quad {text{for }n titulado2}{frac {n}{e^{gamma };log log n+{frac {3}{log log n}}}}quad {text{for }}n>2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d54a7df0105c4627f91ce307dfe4fbeee1a065a0" style="vertical-align: -3.838ex; width:40.996ex; height:6.676ex;"/>

<math alttext="{displaystyle varphi (n)φ φ ()n).neγ γ log⁡ ⁡ log⁡ ⁡ npara infinitamente muchosn.{displaystyle varphi (n) {n}{e^{gamma }log log n}quad {text{for infinitely many }n.}<img alt="{displaystyle varphi (n)

La segunda desigualdad fue mostrada por Jean-Louis Nicolas. Ribenboim dice: "El método de prueba es interesante, ya que la desigualdad se muestra primero bajo el supuesto de que la hipótesis de Riemann es verdadera, y luego bajo el supuesto contrario".

Para el pedido promedio, tenemos

{displaystyle varphi (1)+varphi (2)+cdots +varphi (n)={frac {3n^{2}}{pi ^{2}}}+Oleft(n(log n)^{frac {2}{3}}(log log n)^{frac {4}{3}}right)quad {text{as }}nrightarrow infty}

Debido a Arnold Walfisz, su demostración explota estimaciones sobre sumas exponenciales debidas a I. M. Vinogradov y N. M. Korobov. Mediante una combinación de los métodos de van der Corput y Vinogradov, H.-Q. Liu (Sobre la función de Euler. Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), no. 4, 769–775) mejorado el término de error a

{displaystyle Oleft(n(log n)^{frac {2}{3}}(log log n)^{frac {1}{3}}right)}

(esta es actualmente la estimación más conocida de este tipo). El "Gran O" representa una cantidad que está limitada por una constante multiplicada por la función de $n$ dentro de los paréntesis (que es pequeña en comparación con $n 2$ ).

Este resultado se puede usar para demostrar que la probabilidad de que dos números elegidos al azar sean primos relativos es 6/ $π$ ².

Relación de valores consecutivos

En 1950, Somayajulu demostró

{displaystyle {begin{aligned}lim inf {frac {varphi (n+1)}{varphi (n)}}&=0quad {text{and}}\[5px]lim sup {frac {varphi (n+1)}{varphi (n)}}&=infty.end{aligned}}}

En 1954, Schinzel y Sierpiński reforzaron esto, demostrando que el conjunto

{displaystyle left{{frac {varphi (n+1)}{varphi (n)}},;;n=1,2,ldots right}}

es denso en los números reales positivos. También demostraron que el conjunto

{displaystyle left{{frac {varphi (n)}{n}},;;n=1,2,ldots right}}

es denso en el intervalo (0,1).

Números de pacientes

Un número totient es un valor de la función totient de Euler: es decir, un $m$ para el que hay al menos un $n$ para el que $φ (n) = m$ . La valencia o multiplicidad de un número total $m$ es el número de soluciones a esta ecuación. Un nontotient es un número natural que no es un número totient. Todo entero impar que exceda de 1 es trivialmente un nontotient. También hay un número infinito de no-tocientes pares y, de hecho, todo número entero positivo tiene un múltiplo que es un no-tociente par.

La cantidad de números de totient hasta un límite dado $x$ es

{displaystyle {frac {x}{log x}}e^{{big (}C+o(1){big)}(log log log x)^{2}}}

para una constante $C = 0,8178146...$ .

Si se cuenta de acuerdo con la multiplicidad, la cantidad de números totient hasta un límite dado $x$ es

{displaystyle {Big vert }{n:varphi (n)leq x}{Big vert }={frac {zeta (2)zeta (3)}{zeta (6)}}cdot x+R(x)}

donde el término de error $R$ es de orden máximo $x / (log x) k$ para cualquier $k$ .

Se sabe que la multiplicidad de $m$ supera a $m δ$ infinitamente a menudo para cualquier $δ < 0,55655$ .

Teorema de Ford

Ford (1999) demostró que para cada número entero $k \geq 2$ existe un número totient $m$ de multiplicidad $k$ : es decir, para la cual la ecuación $φ (n) = m$ tiene exactamente $k$ soluciones; este resultado había sido previamente conjeturado por Wacław Sierpiński, y se había obtenido como consecuencia de la hipótesis H de Schinzel. De hecho, cada multiplicidad que ocurre, lo hace infinitamente a menudo.

Sin embargo, ningún número $m$ se conoce con multiplicidad $k = 1$ . La conjetura de la función totient de Carmichael es la afirmación de que no existe tal $m$ .

Números de pacientes perfectos

Un número totient perfecto es un número entero que es igual a la suma de sus totients iterados. Es decir, aplicamos la función totient a un número n, la aplicamos nuevamente al totient resultante, y así sucesivamente, hasta llegar al número 1, y sumamos la secuencia de números resultante; si la suma es igual a n, entonces n es un número total perfecto.

Aplicaciones

Ciclotomía

En la última sección de Disquisitiones, Gauss demuestra que un $n$ -gon regular se puede construir con regla y compás si $φ (n)$ es una potencia de 2. Si $n$ es una potencia de un número primo impar la fórmula para el totient dice que su totient puede ser una potencia de dos solo si $n$ es una primera potencia y $n - 1$ es una potencia de 2. Los números primos que son uno más que una potencia de 2 se llaman primos de Fermat, y solo se conocen cinco: 3, 5, 17, 257 y 65537. Fermat y Gauss los conocían. Nadie ha podido probar si hay más.

Por lo tanto, un $n$ -gon regular tiene una construcción de regla y compás si n es un producto de primos de Fermat distintos y cualquier potencia de 2. Los primeros $n$ son

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40... A003401 en el OEIS).

Teorema de los números primos para progresiones aritméticas

El criptosistema RSA

Configurar un sistema RSA implica elegir números primos grandes $p$ y $q$ , calculando $n = pq$ y $k = φ (n)$ , y encontrar dos números $e$ y $d$ tales que $ed \equiv 1 (mod k)$ . Los números $n$ y $e$ (la "clave de cifrado") se hacen públicos, y $d$ (la " clave de descifrado") se mantiene en privado.

Un mensaje, representado por un número entero $m$ , donde $0 < m < n$ , se cifra calculando $S = m e (modificación n)$ .

Se descifra calculando $t = S d (mod n)$ . El teorema de Euler se puede usar para mostrar que si $0 < t < n$ , luego $t = m$ .

La seguridad de un sistema RSA se vería comprometida si el número $n$ pudiera factorizarse eficientemente o si $φ (n)$ podría calcularse eficientemente sin factorizar $n$ .

Problemas sin resolver

Conjetura de Lehmer

Si $p$ es primo, entonces $φ (p) = p - 1$ . En 1932, D. H. Lehmer preguntó si existen números compuestos $n$ tales que $φ (n)$ divide $n - 1$ . Ninguno es conocido.

En 1933 demostró que si existe tal $n$ , debe ser impar, sin cuadrados y divisible por al menos menos siete números primos (es decir, $ω (n) \geq 7$ ). En 1980, Cohen y Hagis demostraron que $n > 10 20$ y que $ω (n) \geq 14$ . Además, Hagis demostró que si 3 divide $n$ entonces $n > 10 1937042$ y $ω (n) \geq 298848$ .

Conjetura de Carmichael

Esto establece que no hay ningún número $n$ con la propiedad que para todos los demás números $m$ , m ≠ n, φ(m) ≠ φ(n). Consulte el teorema de Ford anterior.

Como se indica en el artículo principal, si hay un solo contraejemplo para esta conjetura, debe haber infinitos contraejemplos, y el más pequeño tiene al menos diez mil millones de dígitos en base 10.

Hipótesis de Riemann

La hipótesis de Riemann es verdadera si y solo si la desigualdad

<math alttext="{displaystyle {frac {n}{varphi (n)}}nφ φ ()n).eγ γ log⁡ ⁡ log⁡ ⁡ n+eγ γ ()4+γ γ − − log⁡ ⁡ 4π π )log⁡ ⁡ n{displaystyle {frac {n}{varphi (n)} {gamma}log log n+{frac {e^{gamma }(4+gamma -log 4pi)}{sqrt {log n}}}}}}}}}}}}}}}}}}} {<img alt="{displaystyle {frac {n}{varphi (n)}}

es cierto para todos los $n \geq p 120569 #$ donde $γ$ es la constante de Euler y $p 120569 #$ es el producto de los primeros $120569$ primos.

Te puede interesar
Vector euclidiano
(leer más)
Te puede interesar
Flexágono
(leer más)
Te puede interesar
Función binaria
(leer más)
Más resultados...

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40