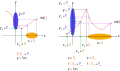Función sobreyectiva

En matemáticas, una función sobreyectiva (también conocida como sobreyección o función sobreyectiva) es una función f que cada elemento y se puede mapear desde el elemento < i>x de modo que f(x) = y. En otras palabras, cada elemento del codominio de la función es la imagen de al menos un elemento de su dominio. No se requiere que x sea único; la función f puede asignar uno o más elementos de X a el mismo elemento de Y.

El término sobreyectiva y los términos relacionados inyectiva y biyectiva fueron introducidos por Nicolas Bourbaki, un grupo de matemáticos del siglo XX, principalmente franceses, que, bajo este seudónimo, escribió una serie de libros que presentan una exposición de las matemáticas avanzadas modernas, a partir de 1935. La palabra francesa sur significa sobre o por encima, y se relaciona con el hecho de que la imagen del dominio de una función sobreyectiva cubre completamente el codominio de la función.

Cualquier función induce una sobreyección restringiendo su codominio a la imagen de su dominio. Toda función sobreyectiva tiene un inverso derecho asumiendo el axioma de elección, y toda función con un inverso derecho es necesariamente una sobreyección. La composición de las funciones sobreyectivas es siempre sobreyectiva. Cualquier función se puede descomponer en una sobreyección y una inyección.

Definición

A función subjetiva es una función cuya imagen es igual a su codominio. Equivalentemente, una función ${displaystyle f}$ con dominio ${displaystyle X}$ y codomain ${displaystyle Sí.$ es subjetivo si por cada ${displaystyle y}$ dentro ${displaystyle Sí.$ existe al menos uno ${displaystyle x}$ dentro ${displaystyle X}$ con ${displaystyle f(x)=y}$. Las supresiones son a veces denotadas por una flecha de dos cabezas hacia la derecha (U+21A0 ↠ DERECHO DE LOS dos HEADED ARROW), como en ${displaystyle fcolon Xtwoheadrightarrow Sí.$.

Simbólicamente,

Si ${displaystyle fcolon Xrightarrow Sí.$, entonces ${displaystyle f}$ se dice que es subjetivo si y sólo si

${displaystyle forall yin Y,,exists xin X,;;f(x)=y}$.

Ejemplos

Una función no quirúrgica desde dominio X al codominio Y. El oval amarillo más pequeño dentro Y es la imagen (también llamada rango) de f. Esta función es no surjetivo, porque la imagen no llena todo el codomain. En otras palabras, Y está coloreado en un proceso de dos pasos: Primero, por cada x dentro X, el punto f()x) es color amarillo; Segundo, el resto de los puntos en Y, que no son amarillos, son de color azul. La función f sólo sería subjetivo si no hubiera puntos azules.

• Para cualquier conjunto X, la función de identidad id_X on X es subjetivo.
• La función f: Z → {0, 1} definidas por f()n) n mod 2 (es decir, incluso los enteros son mapeados a 0 y los números extraños a 1) es subjetivo.
• La función f: R → R definidas por f()x) = 2x + 1 es subjetivo (e incluso bijetivo), porque por cada número real Sí., tenemos un x tales que f()x) Sí.: tal apropiado x es (Sí. −1)/2.
• La función f: R → R definidas por f()x) x³ 3 - 3x es subjetivo, porque la imagen previa de cualquier número real Sí. es el conjunto de solución de la ecuación polinomial cúbica x³ 3 - 3x − Sí. = 0, y cada polinomio cúbico con coeficientes reales tiene al menos una raíz real. Sin embargo, esta función no es inyectable (y por lo tanto no bijetivista), ya que, por ejemplo, la preimage de Sí. = 2 es {x = 1. x = 2}. (De hecho, la preimage de esta función para cada Sí., −2 ≤ Sí. ≤ 2 tiene más de un elemento.)
• La función g: R → R definidas por g()x) x² es no surjetivo, ya que no hay número real x tales que x² = 1 -. Sin embargo, la función g: R → R_≥0 definidas por g()x) x² (con el codominio restringido) es surjetivo, ya que por cada Sí. en el codominio real no negativo Y, hay al menos uno x en el dominio real X tales que x² = Sí..
• La función de logaritmo natural ln: (0, +∞) → R es un subjetivo e incluso bijetivo (a partir del conjunto de números reales positivos al conjunto de todos los números reales). Su inversa, la función exponencial, si se define con el conjunto de números reales como el dominio, no es subjetiva (como su rango es el conjunto de números reales positivos).
• La matriz exponencial no es subjetiva cuando se ve como un mapa desde el espacio de todos n×n matrices a sí misma. Es, sin embargo, generalmente definido como un mapa desde el espacio de todos n×n matrices al grupo lineal general de grado n (es decir, el grupo de todos n×n matrices invertibles). Bajo esta definición, la matriz exponencial es subjetiva para matrices complejas, aunque todavía no subjetiva para matrices reales.
• La proyección de un producto cartesiano A × B a uno de sus factores es subjetivo, a menos que el otro factor esté vacío.
• En un videojuego 3D, los vectores se proyectan en una pantalla plana 2D por medio de una función subjetiva.

Propiedades

Una función es biyectiva si y solo si es tanto sobreyectiva como inyectiva.

Si (como se hace a menudo) una función se identifica con su gráfico, entonces la sobreyectividad no es una propiedad de la función en sí, sino una propiedad del mapeo. Esto es, la función junto con su codominio. A diferencia de la inyectividad, la sobreyectividad no se puede leer solo en el gráfico de la función.

Sobreyecciones como funciones invertibles a la derecha

Se dice que la función g: Y → X es inversa por la derecha de la función f: X → Y si f(g(y)) = y por cada y en Y (g se puede deshacer con f). En otras palabras, g es un inverso derecho de f si la composición f o g de g y f en ese orden es la función de identidad en el dominio Y de g. La función g no necesita ser completamente inversa de f porque la composición en el otro orden, g < small>o f, puede no ser la función de identidad en el dominio X de f. En otras palabras, f puede deshacer o "revertir" g, pero no necesariamente puede ser revertido por él.

Toda función con inversa derecha es necesariamente una sobreyección. La proposición de que toda función sobreyectiva tiene un inverso recto es equivalente al axioma de elección.

Si f: X → Y es sobreyectiva y B< /i> es un subconjunto de Y, entonces f(f ⁻¹(B)) = B. Por lo tanto, B se puede recuperar de su preimagen f ⁻¹(B).

Por ejemplo, en la primera ilustración de arriba, hay una función g tal que g(C) = 4. También hay alguna función f tal que f(4) = C. No importa que g(C) también pueda ser igual a 3; solo importa que f "invierte" g.

Sobreyecciones como epimorfismos

Una función f: X → Y es sobreyectiva si y solo si es cancelativo por la derecha: dada cualquier función g,h: Y → Z, siempre que g o f = h o f, luego g = h. Esta propiedad se formula en términos de funciones y su composición y puede generalizarse a la noción más general de los morfismos de una categoría y su composición. Los morfismos canceladores por la derecha se denominan epimorfismos. En concreto, las funciones sobreyectivas son precisamente los epimorfismos de la categoría de conjuntos. El prefijo epi se deriva de la preposición griega ἐπί que significa sobre, encima, sobre.

Cualquier morfismo con un inverso derecho es un epimorfismo, pero lo contrario no es cierto en general. Un inverso derecho g de un morfismo f se llama sección de f. Un morfismo con un inverso derecho se llama epimorfismo dividido.

Sobreyecciones como relaciones binarias

Cualquier función con dominio X y codominio Y puede verse como una relación binaria total a la izquierda y única a la derecha entre X y < i>Y identificándolo con su función gráfica. Una función sobreyectiva con dominio X y codominio Y es entonces una relación binaria entre X e Y que es recta- único y total a la izquierda y total a la derecha.

Cardinalidad del dominio de una sobreyección

La cardinalidad del dominio de una función sobreyectiva es mayor o igual que la cardinalidad de su codominio: If f: X → Y es una función sobreyectiva, entonces X tiene al menos tantos elementos como Y, en el sentido de los números cardinales. (La prueba apela al axioma de elección para mostrar que una función g: Y → X satisfaciendo f(g(y)) = y para todo y en Y existe. g se ve fácilmente como inyectivo, por lo que la definición formal de |Y| ≤ |X| Está satisfecho.)

Específicamente, si tanto X como Y son finitos con el mismo número de elementos, entonces f: X → Y es sobreyectiva si y solo si f es inyectiva.

Dados dos conjuntos X e Y, la notación X ≤^* Y se usa para decir que X está vacío o que hay una sobreyección de Y a X< /i>. Usando el axioma de elección se puede mostrar que X ≤^* Y y Y ≤^* X juntos implican que |Y | = |X|, una variante del teorema de Schröder-Bernstein.

Composición y descomposición

La composición de las funciones sobreyectivas siempre es sobreyectiva: si f y g son ambas sobreyectivas, y el codominio de g es igual al dominio de f, entonces f o g es sobreyectiva. Por el contrario, si f o g es sobreyectiva, entonces f es sobreyectiva (pero g, la función aplicada primero, no necesita serlo). Estas propiedades se generalizan desde sobreyecciones en la categoría de conjuntos hasta cualquier epimorfismo en cualquier categoría.

Cualquier función se puede descomponer en una sobreyección y una inyección: Para cualquier función h: X → Z existe una sobreyección f: X → Y y una inyección g: Y → Z tal que < i>h = g o f. Para ver esto, defina Y como el conjunto de preimágenes h⁻¹(z< /i>) donde z está en h(X). Estas preimágenes son disjuntas y dividen X. Entonces f lleva cada x al elemento de Y que lo contiene, y g lleva cada elemento de Y al punto en Z al que h envía sus puntos. Entonces f es sobreyectiva ya que es un mapa de proyección, y g es inyectiva por definición.

Sobreyección inducida y biyección inducida

Cualquier función induce una sobreyección restringiendo su codominio a su rango. Cualquier función sobreyectiva induce una biyección definida en un cociente de su dominio colapsando todos los argumentos que se asignan a una imagen fija dada. Más precisamente, cada sobreyección f: A → B se puede factorizar como una proyección seguida por una biyección como sigue. Sean A/~ las clases de equivalencia de A bajo la siguiente relación de equivalencia: x ~ y si y solo si f(x) = f(y). De manera equivalente, A/~ es el conjunto de todas las preimágenes bajo f. Sea P(~): A → A/~ el mapa de proyección que envía cada x en A a su clase de equivalencia [x]_~, y sea f_P : A/~ → B sea la función bien definida dada por f_P([x]_~) = f(x). Entonces f = f_P o P(~).

Espacio de sobreyecciones

Puestos fijos A y B, uno puede formar el conjunto de las suryecciones A ↠ B. La cardenalidad de este conjunto es uno de los doce aspectos de la 12a manera de Rota, y es dada por ${textstyle TENBIA!{begin{Bmatrix}Sobreviértetete en tu vida.$, donde ${textstyle {begin{Bmatrix}Sobrevivir\be1}$ denota un número impresionante de la segunda clase.

Galería

• 

  Composición quirúrgica: la primera función no necesita ser subjetiva.

• 

  Funciones no quirúrgicas en el avión cartesiano. Aunque algunas partes de la función son subjetivas, donde elementos Sí. dentro Y tiene un valor x dentro X tales que Sí. = f()xAlgunas partes no lo son. Izquierda: Hay Sí.₀ dentro Y, pero no hay x₀ dentro X tales que Sí.₀ = f()x₀). Bien. Hay Sí.₁, Sí.₂ y Sí.₃ dentro Y, pero no hay x₁, x₂, y x₃ dentro X tales que Sí.₁ = f()x₁), Sí.₂ = f()x₂), y Sí.₃ = f()x₃).

• 

  Interpretación para funciones subjetivas en el plano cartesiano, definido por el mapeo f: X → Y, donde Sí. = f()x), X = dominio de la función, Y = rango de función. Cada elemento en el rango se asigna desde un elemento en el dominio, por la regla f. Puede haber una serie de elementos de dominio que mapean al mismo elemento de rango. Es decir, todos Sí. dentro Y se mapea desde un elemento x dentro X, más de uno x puede mapa a la misma Sí.. Izquierda: Sólo se muestra un dominio que hace f subjetivo. Bien. dos dominios posibles X₁ y X₂ se muestran.