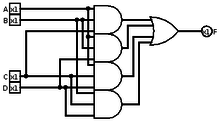
Función mayoritaria

En la lógica booleana, la función mayoritaria (también llamada operador mediano) es la función booleana que se evalúa como falsa cuando la mitad o más de los argumentos son falsos y verdaderos en caso contrario. es decir, el valor de la función es igual al valor de la mayoría de las entradas. Representando los valores verdaderos como 1 y los valores falsos como 0, podemos usar la fórmula (de valor real):

${displaystyle langle p_{1},dotsp_{n}rangle =operatorname {Majority} left(p_{1},dotsp_{n}right)=leftlfloor {fnMicroc {fnK}}+{frac {left(sum) Está bien.$

El "−1/2" en la fórmula sirve para desempatar a favor de ceros cuando el número de argumentos n es par. Si el término "−1/2" se omite, la fórmula se puede usar para una función que rompe empates a favor de unos.

La mayoría de las aplicaciones fuerzan deliberadamente un número impar de entradas para no tener que lidiar con la pregunta de qué sucede cuando exactamente la mitad de las entradas son 0 y exactamente la mitad de las entradas son 1. Los pocos sistemas que calculan la mayoría función en un número par de entradas a menudo están sesgadas hacia "0"—producen "0" cuando exactamente la mitad de las entradas son 0; por ejemplo, una puerta mayoritaria de 4 entradas tiene una salida 0 solo cuando aparecen dos o más 0 en sus entradas. En algunos sistemas, el empate se puede romper al azar.

Circuitos booleanos

Circuito de la mayoría de tres bits

Circuito de la mayoría de cuatro bits

Una puerta mayoritaria es una puerta lógica utilizada en la complejidad de circuitos y otras aplicaciones de circuitos booleanos. Una puerta mayoritaria devuelve verdadero si y solo si más del 50% de sus entradas son verdaderas.

Por ejemplo, en un sumador completo, la salida de acarreo se encuentra aplicando una función mayoritaria a las tres entradas, aunque con frecuencia esta parte del sumador se divide en varias puertas lógicas más simples.

Muchos sistemas tienen redundancia modular triple; utilizan la función mayoritaria para la decodificación lógica mayoritaria para implementar la corrección de errores.

Un resultado importante en la complejidad de los circuitos afirma que la función mayoritaria no puede calcularse mediante circuitos AC0 de tamaño subexponencial.

Propiedades

Para cualquier x, y y z, el operador de mediana ternario ⟨x, y, z⟩ satisface las siguientes ecuaciones.

• .x, Sí., Sí.. Sí.
• .x, Sí., z.z, x, Sí..
• .x, Sí., z.x, z, Sí..
• .x, w, Sí.. w, z.x, w,.Sí., w, z.

Un sistema abstracto que satisface estos axiomas es un álgebra mediana.

Fórmulas monótonas para mayoría

Para n = 1, el operador mediano es solo la operación de identidad unaria x. Para n = 3, el operador mediano ternario se puede expresar usando conjunción y disyunción como xy + yz + zx. Cabe destacar que esta expresión denota la misma operación independientemente de si el símbolo + se interpreta como inclusivo o exclusivo o.

Para un n arbitrario existe una fórmula monótona para la mayoría de tamaño O(n^5.3). Esto se prueba usando el método probabilístico. Por lo tanto, esta fórmula no es constructiva.

Existen enfoques para una fórmula explícita para la mayoría del tamaño del polinomio:

• Tome la mediana de una red de clasificación, donde cada "wire" de comparación y cambio es simplemente una puerta OR y una puerta AND. La construcción de Ajtai-Komlós-Szemerédi (AKS) es un ejemplo.
• Combina las salidas de circuitos de mayoría más pequeños.
• Derandomize la prueba Valiant de una fórmula monotone.