Función legendre

En ciencias físicas y matemáticas, las funciones de Legendre P_λ , Q_λ y funciones de Legendre asociadas P^μ
_λ, Q^μ
_λ, y Las funciones de Legendre del segundo tipo, Q_n, son todas soluciones de Legendre's ecuación diferencial. Los polinomios de Legendre y los polinomios de Legendre asociados también son soluciones de la ecuación diferencial en casos especiales que, en virtud de ser polinomios, tienen una gran cantidad de propiedades adicionales, estructura matemática y aplicaciones. Para estas soluciones polinómicas, consulte los artículos de Wikipedia por separado.

Curvas polinómicas de la leyenda asociada para λ = l = 5.

Ecuación diferencial de Legendre

La ecuación general de Legendre dice

()1− − x2)Sí..− − 2xSí..+[λ λ ()λ λ +1)− − μ μ 21− − x2]Sí.=0,{displaystyle left(1-x^{2}right)y'-2xy'+left[lambda (lambda +1)-{frac # - Sí.

Esta es una ecuación lineal de segundo orden con tres puntos singulares regulares (en 1, −1 y ∞). Como todas esas ecuaciones, se puede convertir en una ecuación diferencial hipergeométrica mediante un cambio de variable, y sus soluciones se pueden expresar mediante funciones hipergeométricas.

Soluciones de la ecuación diferencial

Puesto que la ecuación diferencial es lineal, homogénea (el lado derecho =cero) y de segundo orden, tiene dos soluciones linealmente independientes, que se pueden expresar en términos de la función hipergeométrica, 2F1{displaystyle ¿Qué?. Con .. {displaystyle "Gamma" siendo la función gamma, la primera solución es

1.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Qλ λ μ μ ()z)=π π .. ()λ λ +μ μ +1)2λ λ +1.. ()λ λ +3/2)eiμ μ π π ()z2− − 1)μ μ /2zλ λ +μ μ +12F1()λ λ +μ μ +12,λ λ +μ μ +22;λ λ +32;1z2),paraSilenciozSilencio■1.{displaystyle Q_{lambda}{mu }(z)={frac {sqrt {pi} Gamma (lambda +mu +1)}{2^{lambda #####Gamma (lambda +3/2)}{frac {e^{imupi}(z^{2}-1)^{mu /2}{z^{lambda +mu ################################################################################################################################################################################################################################################################ {fnMicroc {3} {2}}fnMicroc {1} {2}}right),qquad {text{for}\\\\\\\\fnMicroc}}

1.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80f9df625e68fef138049c4ef971d5ece8f3ce85" style="vertical-align: -3.005ex; width:100.332ex; height:7.176ex;"/>

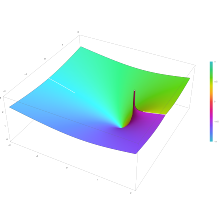
Parcela de la función Legendre del segundo tipo Q n(x) con n=0.5 en el plano complejo de -2-2i a 2+2i con colores creados con función Mathematica 13.1 ComplejoPlot3D

Éstas se conocen generalmente como funciones de Legendre de primer y segundo tipo de grado no entero, con el calificador adicional 'asociado' si μ es distinto de cero. Una relación útil entre las soluciones P y Q es Whipple&# 39;s fórmula.

Orden entero positivo

Para entero positivo μ μ =m▪ ▪ N+{displaystyle mu =min mathbb {N} la evaluación de Pλ λ μ μ {displaystyle P_{lambda} {mu}} arriba implica la cancelación de términos singulares. Podemos encontrar el límite válido para m▪ ▪ N0{displaystyle min mathbb {N} como

Pλ λ m()z)=limμ μ → → mPλ λ μ μ ()z)=()− − λ λ )m()λ λ +1)mm![1− − z1+z]m/22F1()− − λ λ ,λ λ +1;1+m;1− − z2),{displaystyle P_{lambda }{m}(z)=lim _{muto m}P_{lambda }{mu }(z)={frac {(-lambda)_{m}(lambda) [{frac] {1-z}{1+z}derecha] {m/2},_{2}left(-lambdalambda) +1;1+m;{frac {1-z}{2}derecha),}

con ()λ λ )n{displaystyle (lambda)_{n} el símbolo Pochhammer.

Funciones legendre de segunda clase (Qn)

Parcela de las cinco primeras funciones Legendre del segundo tipo.

La no polinización para el caso especial de grado entero λ λ =n▪ ▪ N0{displaystyle lambda =nin mathbb {N}, y μ μ =0{displaystyle mu =0}, se discute a menudo por separado. Es dado por

Qn()x)=n!1⋅ ⋅ 3⋯ ⋯ ()2n+1)()x− − ()n+1)+()n+1)()n+2)2()2n+3)x− − ()n+3)+()n+1)()n+2)()n+3)()n+4)2⋅ ⋅ 4()2n+3)()2n+5)x− − ()n+5)+⋯ ⋯ ){cn} {ccn} {ccn}cdot 3cdots (2n+1)}}left(x^{-n+1)}+{frac {(n+1)}{2}n+3)} {cc} {ccc} {cccn2}

Esta solución es necesariamente singular cuando x=± ± 1{displaystyle x=pm 1}.

Las funciones de Legendre del segundo tipo también se pueden definir recursivamente a través de la fórmula recursiva de Bonnet

Qn()x)={}12log⁡ ⁡ 1+x1− − xn=0P1()x)Q0()x)− − 1n=12n− − 1nxQn− − 1()x)− − n− − 1nQn− − 2()x)n≥ ≥ 2.{displaystyle Q_{n}(x)={begin{cases}{frac {1}{2}log {frac} {1+x}{1-x} {0P_{1}(x)Q_{0}(x)-1 implican=1\\{n-1}{n}}x_{n-1}(x)-{frac} {n-1} {n}Q_{n-2}(x) Damengeq 2,end{cases}}

Funciones de Legendre asociadas de segundo tipo

Solución no polinómica para el caso especial de grado entero λ λ =n▪ ▪ N0{displaystyle lambda =nin mathbb {N}, y μ μ =m▪ ▪ N0{displaystyle mu =min mathbb {N} es dado por

Qnm()x)=()− − 1)m()1− − x2)m2dmdxmQn()x).{displaystyle Q_{n} {m}(x)=(-1)^{m}(1-x^{2})^{frac} {m} {m} {fn} {fn} {fn} {fn} {fn} {fn} {fn} {fn} {fn}fn} {fn}fnfnfn} {fnfnfnfnMicrosoft}}}} {fnfnfn}}}}fnfnfnfnfnfnfnfnfnfnfnfnfnfnKfnfnfn}fnfnfnfnfnfnfnfnKfnhnKfn}fn}fnfn}fnfnKfnfn}fnfn}fn}fnfn}fnfn}fnfn}fn}fn

Representaciones integrales

Las funciones de Legendre se pueden escribir como integrales de contorno. Por ejemplo,

Pλ λ ()z)=Pλ λ 0()z)=12π π i∫ ∫ 1,z()t2− − 1)λ λ 2λ λ ()t− − z)λ λ +1dt{displaystyle P_{lambda }(z)=P_{lambda }{0}(z)={frac {1}{2pi i}}int _{1,z}{frac {(t^{2}-1)^{lambda ##{2^{lambda }(t-z)# - ¡No!

Ps()x)=12π π ∫ ∫ − − π π π π ()x+x2− − 1#⁡ ⁡ Silencio Silencio )sdSilencio Silencio =1π π ∫ ∫ 01()x+x2− − 1()2t− − 1))sdtt()1− − t),s▪ ▪ C{displaystyle P_{s}(x)={frac {1}{2pi}int _{-pi }{pi }left(x+{sqrt {x^{2}-1}cos theta right)^{s}dtheta {fnMicroc {1}int _{0}{1}left(x+{sqrt {x^{2}-1} {2t-1)right)}{s}{s}{frac {sqrt {t(1-t)}}}}}}qquad sin mathbb {C}

La leyenda funciona como personajes

La representación integral real Ps{displaystyle P_{s} son muy útiles en el estudio del análisis armónico sobre L1()G//K){displaystyle L^{1}(G//K)} Donde G//K{displaystyle G/K} es el espacio de doble conjunto de SL()2,R){displaystyle SL(2,mathbb {R}} (ver función esférica Zonal). En realidad el Fourier se transforma en L1()G//K){displaystyle L^{1}(G//K)} es dado por

L1()G//K)∋ ∋ f↦ ↦ f^ ^ {displaystyle L^{1}(G//K)ni fmapsto {hat {f}}

f^ ^ ()s)=∫ ∫ 1JUEGO JUEGO f()x)Ps()x)dx,− − 1≤ ≤ R R ()s)≤ ≤ 0{displaystyle {hat {f}(s)=int _{1}{infty }f(x)P_{s}(x)dx,qquad -1leq Re (s)leq 0}