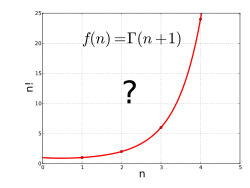
Función gamma

ImprimirCitar

En matemáticas, la función gamma (representada por $Γ$ , la letra mayúscula gamma del alfabeto griego) es una extensión comúnmente utilizada del factorial Función a números complejos. La función gamma se define para todos los números complejos excepto los enteros no positivos. Para cada entero positivo $n$ ,

{displaystyle Gamma (n)=(n-1)!,}

Derivada por Daniel Bernoulli, para números complejos con una parte real positiva, la función gamma se define a través de una integral impropia convergente:

{displaystyle Gamma (z)=int ¿Por qué?

La función gamma entonces se define como la continuación analítica de esta función integral a una función meromórfica que es holomorfa en todo el plano complejo excepto el cero y los enteros negativos, donde la función tiene polos simples.

La función gamma no tiene ceros, por lo que la función gamma recíproca $1 / Γ(z)$ es una función completa. De hecho, la función gamma corresponde a la transformada de Mellin de la función exponencial negativa:

{displaystyle Gamma (z)={mathcal {M}{e^{-x}}(z),}

Existen otras extensiones de la función factorial, pero la función gamma es la más popular y útil. Es un componente de varias funciones de distribución de probabilidad y, como tal, es aplicable en los campos de probabilidad y estadística, así como en combinatoria.

Motivación

La función gamma interpola la función factorial a valores no enteros.

La función gamma puede verse como una solución al siguiente problema de interpolación:

"Encontrar una curva suave que conecta los puntos

() x, Sí.)

dado por

Sí. = x - 1).

en los valores enteros positivos para

x

Un gráfico de los primeros factoriales deja claro que se puede dibujar una curva de este tipo, pero sería preferible tener una fórmula que describa con precisión la curva, en la que el número de operaciones no dependa del tamaño de $x$ . ¡La fórmula simple para el factorial, $x! = 1 \times 2 \times \dots \times x$ , no se puede usar directamente para valores no enteros de $x$ ya que solo es válido cuando $x$ es un número natural (o entero positivo). En términos relativos, no existen soluciones tan simples para los factoriales; ninguna combinación finita de sumas, productos, potencias, funciones exponenciales o logaritmos será suficiente para expresar $x!$ ; pero es posible encontrar una fórmula general para factoriales utilizando herramientas como integrales y límites del cálculo. Una buena solución a esto es la función gamma.

Hay infinitas extensiones continuas del factorial a números no enteros: se pueden dibujar infinitas curvas a través de cualquier conjunto de puntos aislados. La función gamma es la solución más útil en la práctica, siendo analítica (excepto en los números enteros no positivos), y se puede definir de varias formas equivalentes. Sin embargo, no es la única función analítica que extiende el factorial, ya que le agrega cualquier función analítica que sea cero en los enteros positivos, como $k sin mπx$ para un entero $m$ , dará otra función con esa propiedad. Tal función se conoce como función pseudogamma, siendo la más famosa la función de Hadamard.

La función gamma,

. z)

en azul, trazado junto con

. z) + pecado(π) z)

en verde. Observe la intersección en números enteros positivos. Ambos son continuaciones analíticas válidas de los factoriales a los no-integers.

Una propiedad más restrictiva que satisfacer la interpolación anterior es satisfacer la relación de recurrencia que define una versión traducida de la función factorial,

{displaystyle f(1)=1,}

{displaystyle f(x+1)=xf(x),}

para cualquier número real positivo $x$ . Pero esto permitiría la multiplicación por cualquier función $g () x)$ satisfaciendo ambos $g () x) g () x +1)$ para todos los números reales $x$ y $g (0) = 1$ , como la función $g () x) e k pecado 2mπx$ . Una de varias maneras de resolver la ambigüedad viene del teorema Bohr-Mollerup. Dice que cuando la condición $f$ ser logaritmically convex (o "super-convex", significa que ${displaystyle ln circ f}$ es convex) se añade, determina únicamente $f$ para entradas positivas y reales. Desde allí, la función gamma se puede extender a todos los valores reales y complejos (excepto los enteros negativos y cero) utilizando la continuación analítica única de $f$ .

Definición

Definición principal

La notación ${displaystyle Gamma (z)}$ es debido a Legendre. Si la parte real del número complejo $z$ es estrictamente positivo ( ${displaystyle Re (z)}$ ), entonces el integral

{displaystyle Gamma (z)=int ¿Qué?

converge absolutamente, y se conoce como la integral de Euler de segunda especie. (La integral de Euler del primer tipo es la función beta). Usando la integración por partes, se ve que:

Parcela de función gamma en plano complejo en 3D con color y leyenda y 1000 puntos de trama creados con Mathematica

{displaystyle {begin{aligned}Gamma (z+1) ¿Qué? Bigl. ################################################################################################################################################################################################################################################################ ¿Qué?

Reconociendo que ${displaystyle -t^{z}e^{-t}to 0}$ como ${displaystyle tto infty}$

{displaystyle {begin{aligned}Gamma (z+1) ¿Por qué?

Podemos calcular ${displaystyle Gamma (1)}$ :

{displaystyle {begin{aligned}Gamma (1) ¿Por qué? ¿Por qué? [}-e^{-t}{ Grande ####### {infty }\fncipl_toinfty }left(-e^{-t}right)-left(-e^{-0}right)\=0-(-1)\fnunció=1.end{aligned}}}}}}}

Dado que ${displaystyle Gamma (1)=1}$ y ${displaystyle Gamma (n+1)=nGamma (n),}$

{displaystyle Gamma (n)=1cdot 2cdot 3cdots (n-1)=(n-1)}

para todos los enteros positivos $n$ . Esto puede verse como un ejemplo de demostración por inducción.

La identidad ${textstyle Gamma (z)={frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}} {fnMicrosoft Sans Serif}}} {fn}}}}} {fnK}}}}}}} {\fnK}}}}}}}} {cH}}}}}}}}}}}}}}}$ se puede utilizar (o, dando el mismo resultado, la continuación analítica se puede utilizar) para ampliar únicamente la formulación integral para ${displaystyle Gamma (z)}$ a una función meromorfa definida para todos los números complejos $z$ , excepto números inferiores o iguales a cero. Es esta versión extendida que se conoce comúnmente como la función gamma.

Definiciones alternativas

La definición de Euler como producto infinito

Cuando busca aproximarse ${displaystyle z!}$ para un número complejo ${displaystyle z}$ , es eficaz para el primer cálculo ${displaystyle n!}$ para un entero grande ${displaystyle n}$ . Use eso para aproximar un valor para ${displaystyle (n+z)}$ , y luego utilizar la relación de recursión ${displaystyle m!=m(m-1)}$ al revés ${displaystyle n}$ tiempos, para desenrollarlo a una aproximación para ${displaystyle z!}$ . Además, esta aproximación es exacta en el límite como ${displaystyle n}$ va al infinito.

Específicamente, para un entero fijo ${displaystyle m}$ , es el caso de que

{displaystyle lim _{nto infty }{frac {n!,left(n+1right)^{m}{(n+m)}}}=1,}} {cHFF}

Si ${displaystyle m}$ no es un entero entonces no es posible decir si esta ecuación es verdadera porque todavía no hemos definido (en esta sección) la función factorial para los no-integers. Sin embargo, tenemos una extensión única de la función factorial a los no-integers insistiendo en que esta ecuación continúe manteniendo cuando el entero arbitrario ${displaystyle m}$ es reemplazado por un número complejo arbitrario ${displaystyle z}$ .

{displaystyle lim _{nto infty }{frac {n!,left(n+1right)^{z}{(n+z)}}}=1,}}

Multiplicar ambos lados por ${displaystyle z!}$ da

{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ¿Qué? {1}{1+{frac} {Z} {n}}}left(1+{frac {1}{n}right)^{z}right].end{aligned}}}

Este producto infinito converge para todos los números complejos ${displaystyle z}$ excepto los enteros negativos, que fallan porque intentan usar la relación de recursión ${displaystyle m!=m(m-1)}$ a través del valor ${displaystyle m=0}$ implica una división por cero.

Del mismo modo para la función gamma, la definición como un producto infinito debido a Euler es válida para todos los números complejos ${displaystyle z}$ excepto los enteros no positivos:

{displaystyle "Gamma (z)={frac {1}{z}prod ¿Por qué? {Z}}},}

Por esta construcción, la función gamma es la función única que se satisface simultáneamente ${displaystyle Gamma (1)=1}$ , ${displaystyle Gamma (z+1)=zGamma (z)}$ para todos los números complejos ${displaystyle z}$ excepto los enteros no positivos, y ${textstyle lim _{nto infty}{frac {Gamma (n+z)}{Gamma (n);n^{z}}}=1}$ para todos los números complejos ${displaystyle z}$ .

Definición de Weierstrass

La definición de la función gamma debida a Weierstrass también es válida para todos los números complejos $z$ excepto los números enteros no positivos:

{displaystyle Gamma (z)={frac {e^{-gamma } {z}prod ¿Por qué?

Donde ${displaystyle gamma approx 0.577216}$ es la constante Euler-Mascheroni. Este es el producto de Hadamard ${displaystyle 1/Gamma (z)}$ en una forma reescrita. Ciertamente, desde ${displaystyle 1/Gamma (z)}$ está completo del género 1 con un simple cero ${displaystyle z=0}$ , tenemos la representación del producto

{fnMicroc} {1}{rho }}=ze^{Az+B}prod _{rho }left(1-{frac {z} {rho }}right)e^{z/rho }}} {fnK}

Parcela de argumento absoluto de la función gamma de z=-4 a 7 creada en Mathematica 13.1

donde el producto está sobre los ceros ${displaystyle rho neq 0}$ de ${displaystyle 1/Gamma (z)}$ . Desde ${displaystyle Gamma (z)}$ tiene postes simples en los enteros no positivos, sigue ${displaystyle 1/Gamma (z)}$ tiene ceros simples en los enteros no positivos, y por lo tanto la ecuación anterior se convierte en fórmula de Weierstrass con ${displaystyle -Az-B.$ en lugar de ${displaystyle - 'gamma z'$ . La derivación de las constantes ${displaystyle A=gamma }$ y ${displaystyle B=0}$ es algo técnico, pero se puede lograr utilizando algunas identidades que implican la función Riemann zeta (véase esta identidad, por ejemplo). Vea también el teorema de factorización Weierstrass.

Propiedades

Generales

Otras ecuaciones funcionales importantes para la función gamma son la fórmula de reflexión de Euler

{displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin pi z}}},qquad znot in mathbb {Z}

lo que implica

{displaystyle Gamma (z-n)=(-1)^{n-1};{frac {Gamma (-z)Gamma (1+z)}{Gamma (n+1-z)}}},qquad nin mathbb {Z}

y la fórmula de duplicación de Legendre

{displaystyle Gamma (z)Gamma left(z+{tfrac {1}{2}right)=2^{1-2z};{sqrt {pi} };Gamma (2z). }

Derivación de la fórmula de reflexión de Euler
Desde ${displaystyle e^{-t}=lim _{nto infty }left(1-{frac {t} {n}right)}{n}}$ la función gamma se puede representar como ${displaystyle Gamma (z)=lim _{nto infty }int _{0}{n}t^{z-1}left(1-{frac {t}right)^{n},dt.}$ Integración por partes ${displaystyle n}$ rendimientos de tiempos ${displaystyle Gamma (z)=lim _{nto infty }{frac {nz}cdot {frac {n-1}{n(z+1)}cdot {frac {n-2}{n(z+2)}}cdots {frac {1}{nnn1} {n1}}} {cdot}}} {cdot}cdot}cdot}cdot}cdot}cdot {cdot {cdot {cdot}cdot {cdot}cdot}cdot {cdot}cdot {cdot {cdot {cdot}cdot {cdot {cdot {cdot {cdot {c}c}cdot {cdot {cdot}cdot {cdot {c ¿Qué?$ que es igual a ${displaystyle Gamma (z)=lim _{nto infty }{frac {n}{n^{n}}}left(prod) ¿Por qué?$ Esto puede ser reescrito como ${displaystyle Gamma (z)=lim _{nto infty }{frac {n^{z}{z}}prod} ¿Qué? {k}{z+k}=lim _{nto infty}{frac {n^{z}{z}}prod} ¿Qué? {1}{1+{frac}.$ Podemos utilizar esto para evaluar el lado izquierdo de la fórmula de reflexión: ${displaystyle Gamma (1-z)Gamma (z)=-zGamma (-z)Gamma (z)=lim _{nto infty }{frac {1}prod - ¿Qué? {1}{1-{frac {Z^{2}}}}}}$ Puede probarse que ${displaystyle sin pi z=pi zprod ¿Qué? {Z^{2}{k^{2}}derecha).}$ Entonces... ${fnMicroc {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fnMin ♫{sin {fn}=lim _{ntoinfty}{frac {1}{z}prod} ¿Qué? {1}{1-{frac {fnMicrosoft Sans Serif}}$ La fórmula de reflexión de Euler sigue: ${displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin pi z}},qquad znot in mathbb {Z}$

Derivación de la fórmula de reflexión de Euler

Desde ${displaystyle e^{-t}=lim _{nto infty }left(1-{frac {t} {n}right)}{n}}$

la función gamma se puede representar como

{displaystyle Gamma (z)=lim _{nto infty }int _{0}{n}t^{z-1}left(1-{frac {t}right)^{n},dt.}

Integración por partes ${displaystyle n}$ rendimientos de tiempos

{displaystyle Gamma (z)=lim _{nto infty }{frac {nz}cdot {frac {n-1}{n(z+1)}cdot {frac {n-2}{n(z+2)}}cdots {frac {1}{nnn1} {n1}}} {cdot}}} {cdot}cdot}cdot}cdot}cdot}cdot {cdot {cdot {cdot}cdot {cdot}cdot}cdot {cdot}cdot {cdot {cdot {cdot}cdot {cdot {cdot {cdot {cdot {c}c}cdot {cdot {cdot}cdot {cdot {c ¿Qué?

que es igual a

{displaystyle Gamma (z)=lim _{nto infty }{frac {n}{n^{n}}}left(prod) ¿Por qué?

Esto puede ser reescrito como

{displaystyle Gamma (z)=lim _{nto infty }{frac {n^{z}{z}}prod} ¿Qué? {k}{z+k}=lim _{nto infty}{frac {n^{z}{z}}prod} ¿Qué? {1}{1+{frac}.

Podemos utilizar esto para evaluar el lado izquierdo de la fórmula de reflexión:

{displaystyle Gamma (1-z)Gamma (z)=-zGamma (-z)Gamma (z)=lim _{nto infty }{frac {1}prod - ¿Qué? {1}{1-{frac {Z^{2}}}}}}

Puede probarse que

{displaystyle sin pi z=pi zprod ¿Qué? {Z^{2}{k^{2}}derecha).}

Entonces...

{fnMicroc {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fnMin ♫{sin {fn}=lim _{ntoinfty}{frac {1}{z}prod} ¿Qué? {1}{1-{frac {fnMicrosoft Sans Serif}}

La fórmula de reflexión de Euler sigue:

{displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin pi z}},qquad znot in mathbb {Z}

Derivación de la fórmula de duplicación Legendre
La función beta puede ser representada como ${displaystyle mathrm {B} (z_{1},z_{2}={frac} Gamma (z_{1} Gamma (z_{1}+z_{2}}=int ¿Qué?$ Ajuste ${displaystyle z_{1}=z_{2}=z}$ rendimientos ${displaystyle {frac}=int ¿Qué?$ Después de la sustitución ${displaystyle t={frac {1+u}{2}}$ nosotros ${displaystyle {frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {1}{22z-1}} {fnMicrosoft Sans Serif}} {fnMicroc {fnMicroc {fnMicroc}}}} {f}}}f}}}}}}}}f}}}f}f}}}}f}f}f}f}}f}f}f}f}f}f}f}fnun} ¿Por qué?$ La función ${displaystyle (1-u^{2}$ es incluso, por lo tanto ${displaystyle 2^{2z-1}Gamma ^{2}(z)=2Gamma (2z)int ¿Qué?$ Ahora asume ${displaystyle mathrm {B} left({frac {1}{2}},zright)=int ¿Por qué?$ Entonces... ${displaystyle mathrm {B} left({frac {1}{2}},zright)=2int ¿Por qué?$ Esto implica ${displaystyle 2^{2z-1}Gamma ^{2}(z)=Gamma (2z)mathrm {B}left({frac {1}{2}},zright). }$ Desde ${displaystyle mathrm {B} left({frac {1}{2}},zright)={frac {Gamma left({frac {1}{2}derecha)Gamma (z)}{ Gamma left(z+{2}right)},quad Gamma left({frac {1}{2}right)={sqrt {pi }}}}}}$ la fórmula de duplicación Legendre sigue: ${displaystyle Gamma (z)Gamma left(z+{frac {1}{2}right)=2^{1-2z}{sqrt {pi} };Gamma (2z). }$

Derivación de la fórmula de duplicación Legendre

La función beta puede ser representada como

{displaystyle mathrm {B} (z_{1},z_{2}={frac} Gamma (z_{1} Gamma (z_{1}+z_{2}}=int ¿Qué?

Ajuste ${displaystyle z_{1}=z_{2}=z}$ rendimientos

{displaystyle {frac}=int ¿Qué?

Después de la sustitución ${displaystyle t={frac {1+u}{2}}$ nosotros

{displaystyle {frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {1}{22z-1}} {fnMicrosoft Sans Serif}} {fnMicroc {fnMicroc {fnMicroc}}}} {f}}}f}}}}}}}}f}}}f}f}}}}f}f}f}f}}f}f}f}f}f}f}f}fnun} ¿Por qué?

La función ${displaystyle (1-u^{2}$ es incluso, por lo tanto

{displaystyle 2^{2z-1}Gamma ^{2}(z)=2Gamma (2z)int ¿Qué?

Ahora asume

{displaystyle mathrm {B} left({frac {1}{2}},zright)=int ¿Por qué?

Entonces...

{displaystyle mathrm {B} left({frac {1}{2}},zright)=2int ¿Por qué?

Esto implica

{displaystyle 2^{2z-1}Gamma ^{2}(z)=Gamma (2z)mathrm {B}left({frac {1}{2}},zright). }

Desde

{displaystyle mathrm {B} left({frac {1}{2}},zright)={frac {Gamma left({frac {1}{2}derecha)Gamma (z)}{ Gamma left(z+{2}right)},quad Gamma left({frac {1}{2}right)={sqrt {pi }}}}}}

la fórmula de duplicación Legendre sigue:

{displaystyle Gamma (z)Gamma left(z+{frac {1}{2}right)=2^{1-2z}{sqrt {pi} };Gamma (2z). }

La fórmula de duplicación es un caso especial del teorema de la multiplicación (Ver, Ec. 5.5.6)

{displaystyle prod _{k=0}^{m-1}Gamma left(z+{frac {k}{m}}right)=(2pi)^{frac {m-1}{2};m^{frac} {1}{2}-mz};Gamma (mz).}

Una propiedad simple pero útil, que se puede ver en la definición de límite, es:

{fnMicrosoft Sans Serif}= Gamma ({overline {z}});Rightarrow ;Gamma (z)Gamma ({overline {z}})in mathbb {R}.}

En particular, con $z = a + bi$ , este producto es

{displaystyle SilencioGamma (a+bi) Gamma (a) forever^{2}prod _{k=0}{infty }{frac {1}{1+{frac {b^{2}}{(a+k)}}}}}}}}}

Si la parte real es un número entero o un medio entero, esto se puede expresar finitamente en forma cerrada:

{displaystyle {begin{aligned} Gamma (bi) sometida^{2}={frac {pi }{bsinhpi b}[6pt]left WordPressGamma left({tfrac {1}{2}}+biright)derechaurdo {fnMicrosoft Sans Serif}\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} b}{sinhpi b}\\left uponGammaleft(1+n+biright)right WordPress^{2} limit={frac {pi b}{pehpi b}prod _{k=1}n}left(k^{2}+b^{2}right),quad nin mathbb {N}\\left WordPressGammaleft(-n+biright)right sometida^{2} severo={frac {pi }{bsinh pi B. ¿Por qué? {N}\\fnMicroc {1}pm n+biright)right sobre la vida actual{2} limit={frac {pic} }{cosh pi B. ¿Por qué? {1}{2}right)^{2}+b^{2}right)^{pm 1},quad nin mathbb {N} end{aligned}}

Prueba de fórmulas de valor absoluto para argumentos de parte real entero o medio entero
Primero, considere la fórmula de reflexión aplicada a ${displaystyle z=bi}$ . ${displaystyle Gamma (bi)Gamma (1-bi)={frac {pi }{sin pi bi}}}$ Aplicando la relación de recurrencia al segundo mandato, tenemos ${displaystyle -bicdot Gamma (bi)Gamma (-bi)={frac {pi }{sin pi bi}}}$ que con simple reorganización da ${displaystyle Gamma (bi)Gamma (-bi)={frac {pi }{-bisin pi ¿Qué? }{bsinh pi - Sí.$ Segundo, considere la fórmula de reflexión aplicada a ${displaystyle z={tfrac {1}{2}+bi}$ . ${displaystyle Gamma ({tfrac {1}{2}+bi)Gamma left(1-({tfrac {1}{2}+bi)right)= Gamma ({tfrac {1}+bi) Gamma ({tfrac {1}{2}-bi)={frac {pi {fnMicrosoft Sans Serif}}={frac {pi}{fnMicroc {pi}{cos pi ¿Qué? }{cosh pi - Sí.$ Formulas para otros valores ${displaystyle z}$ para el cual la parte real es entero o medio entero rápidamente sigue por inducción utilizando la relación recurrencia en las direcciones positivas y negativas.

Prueba de fórmulas de valor absoluto para argumentos de parte real entero o medio entero

Primero, considere la fórmula de reflexión aplicada a ${displaystyle z=bi}$ .

{displaystyle Gamma (bi)Gamma (1-bi)={frac {pi }{sin pi bi}}}

Aplicando la relación de recurrencia al segundo mandato, tenemos

{displaystyle -bicdot Gamma (bi)Gamma (-bi)={frac {pi }{sin pi bi}}}

que con simple reorganización da

{displaystyle Gamma (bi)Gamma (-bi)={frac {pi }{-bisin pi ¿Qué? }{bsinh pi - Sí.

Segundo, considere la fórmula de reflexión aplicada a ${displaystyle z={tfrac {1}{2}+bi}$ .

{displaystyle Gamma ({tfrac {1}{2}+bi)Gamma left(1-({tfrac {1}{2}+bi)right)= Gamma ({tfrac {1}+bi) Gamma ({tfrac {1}{2}-bi)={frac {pi {fnMicrosoft Sans Serif}}={frac {pi}{fnMicroc {pi}{cos pi ¿Qué? }{cosh pi - Sí.

Formulas para otros valores ${displaystyle z}$ para el cual la parte real es entero o medio entero rápidamente sigue por inducción utilizando la relación recurrencia en las direcciones positivas y negativas.

Quizás el valor más conocido de la función gamma en un argumento no entero es

{displaystyle "Gamma left" ({tfrac {1}{2}right)={sqrt {pi }}

que se puede encontrar por ${textstyle z={frac {1}{2}}}$ en las fórmulas de reflexión o duplicación, utilizando la relación con la función beta que se da a continuación ${textstyle z_{1}=z_{2}={frac {1}{2}}}$ , o simplemente haciendo la sustitución ${displaystyle u={sqrt {z}}$ en la definición integral de la función gamma, dando como resultado una integral gasiana. En general, para valores enteros no negativos ${displaystyle n}$ tenemos:

{displaystyle {begin{aligned}Gamma left({tfrac {1}{2}}+nright) {={(2n)! {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}f} {fnMicrosoft Sans} {f}f}fnMicrosoft Sans}fnMicrosoft SanscH0}¡No! ¡No! # }={binom {n-{frac {1}{2}} {n}n} {sqrt {pi}}[8pt]Gamma left({tfrac {1} {2}-nright)} {={(-4)^{n}n} {n]}{sqrt {pirt {i} {i}ni} {i} {i}}} {n}}} {n}}}} {n}}} {n}}}} {n}}}} {n}n} {n}}} {n}} {n}}}} {n}}}}} {n}} {n}}}}} {n} {n}}}} {n}} {n}n}}}}}}}}}}}}}}} {n} {n} {n} {n}}}}} {n}}}}}}} {n}}}}} {n} {fn} {fn} {fn1}}} {sqrt {pi}}} {sqrt {pi)} {sqrt {pi}} {fn1}}} {sqrt {sqrt {pi! }={frac {sqrt {pi} }{binom {-1/2} {n}n} {-end{aligned}}}

donde el doble factorial ${displaystyle (2n-1)!=(2n-1)(2n-3)cdots (3)(1)}$ . Ver Valores particulares de la función gamma para valores calculados.

Podría ser tentador generalizar el resultado de que ${textstyle Gamma left {frac {2}right)={sqrt {pi} }$ buscando una fórmula para otros valores individuales ${displaystyle Gamma (r)}$ Donde ${displaystyle r}$ es racional, especialmente porque según el teorema digamma de Gauss, es posible hacerlo por la función digamma estrechamente relacionada a cada valor racional. Sin embargo, estos números ${displaystyle Gamma (r)}$ no se sabe que son expresibles por sí mismos en términos de funciones elementales. Se ha demostrado que ${displaystyle Gamma (n+r)}$ es un número trascendental y algebraicamente independiente de ${displaystyle pi}$ para cualquier entero ${displaystyle n}$ y cada una de las fracciones ${textstyle r={frac {1}{6}},{frac {4}} {frac {1}{3}},{frac {2}{3}}}} {frac {3}{4}},{frac {frac}} {frac} {f}}} {f}}} {f}}}} {f} {f}f}}}}}}f}f}f}f}f}f}f}f} {f} {f} {f}f} {f} {f}f}f}f}f}f}f}f}f}f}}f}f}f}f}fnf}f}f}f}fnf}f}f}fnfnfnfnfnfnfnfnf}fnh00}f}fn {5}{6}}$ . En general, al calcular los valores de la función gamma, debemos establecernos para aproximaciones numéricas.

Las derivadas de la función gamma se describen en términos de la función poligamma, $ψ (0) (z)$ :

{displaystyle Gamma '(z)=Gamma (z)psi ^{(0)}(z). }

Para un entero positivo $m$ , la derivada de la función gamma se puede calcular de la siguiente manera:

Parcela de la función gamma en el plano complejo desde

-2-2 i

6+2 i

con colores creados en Mathematica

{displaystyle Gamma '(m+1)=m!left(-gamma +sum _{k=1}^{m}{frac {1}{k}right)=m!left(-gamma +H(m)right),}

donde H(m) es el m-ésimo número armónico y $γ$ es la constante de Euler-Mascheroni.

Para ${displaystyle Re (z)}$ el ${displaystyle n}$ th derivative of the gamma function is:

{displaystyle {fn} {fn} {fn}} {fn}} {fn}} {fn}} {fn}}}} {fn}}}}} {fn}}}}}}}} {f}}} {fn}}}}}}}}}}}}}}}}}} Gamma (z)=int _{0} {infty }t^{z-1}e^{-t}(ln t)^{n},dt.}

(Esto puede derivarse diferenciando la forma integral de la función gamma con respecto a ${displaystyle z}$ , y utilizando la técnica de diferenciación bajo el signo integral.)

Uso de la identidad

{displaystyle Gamma ^{(n)}(1)=(-1)^{n}n!sum limits _{pi ,vdash ,n}prod _{i=1}{r}{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {cdot} a_{i}}qquad zeta ^{*}(x):={begin{cases}zeta (x) limitadaxneq 1\\gamma &x=1end{cases}}

Donde ${displaystyle zeta (z)}$ es la función Riemann zeta, y ${displaystyle pi}$ es una partición de ${displaystyle n}$ dado por

{displaystyle pi =underbrace {a_{1}+cdots +a_{1} _{k_{1} {text{ terms}}}+cdots +underbrace {a_{r}+cdots - ¿Qué?

tenemos en particular la expansión en serie de Laurent de la función gamma

{displaystyle Gamma (z)={1}{z}-gamma +{tfrac {1}{2}left(gamma ^{2}+{frac {pic {pic}}left ¿Qué? ^{2}{2}}+2zeta (3)right)z^{2}+O(z^{3}). }

Desigualdades

Cuando se restringe a los números reales positivos, la función gamma es una función estrictamente logarítmicamente convexa. Esta propiedad puede expresarse de cualquiera de las siguientes tres formas equivalentes:

Para cualquier dos números reales positivos ${displaystyle x_{1}}$ y ${displaystyle x_{2}$ , y para cualquier ${displaystyle tin [0,1]}$ , ${displaystyle Gamma (tx_{1}+(1-t)x_{2})leq Gamma (x_{1} {t}Gamma (x_{2})^{1-t}$
Para cualquier dos números reales positivos ${displaystyle x_{1}}$ y ${displaystyle x_{2}$ , y ${displaystyle x_{2}$ ■ ${displaystyle x_{1}}$ ${displaystyle left({frac Vale. {1}{x_{2}-x_{1}}} {frac {Gamma '(x_{1}}{Gamma (x_{1}}}}}derecha). }$
Para cualquier número real positivo ${displaystyle x}$ , ${displaystyle Gamma ''(x)Gamma (x)Gamma '(x)^{2}.}$

La última de estas declaraciones es, esencialmente por definición, la misma que la declaración de que ${displaystyle psi ^{(1)}(x) título0}$ , donde ${displaystyle psi ^{(1)}$ es la función poligamma del orden 1. Para probar la convexidad logarítmica de la función gamma, basta observar que ${displaystyle psi ^{(1)}$ tiene una representación de serie que, para positivo real $x$ , consta de sólo términos positivos.

La convexidad logarítmica y la desigualdad de Jensen juntos implican, para cualquier número real positivo ${displaystyle x_{1},ldotsx_{n}$ y ${displaystyle a_{1},ldotsa_{n}$ ,

{displaystyle Gamma left({frac {a_{1}x_{1}+cdots ##a_{n}x_{n}{a_{1}+cdots ¿Qué? "Gamma" (x_{n} {n}{bigr)}{frac {1}{a_{1}+cdots - Sí.

También hay límites en las proporciones de las funciones gamma. La más conocida es la desigualdad de Gautschi, que dice que para cualquier número real positivo $x$ y cualquier s ∈ (0, 1),

{displaystyle x^{1-s} frac {Gamma (x+1)}{Gamma (x+s)} {left(x+1right)^{1-s}.}

Fórmula de Stirling

Representación de la función gamma en el plano complejo. Cada punto

{displaystyle z}

es coloreado según el argumento de

{displaystyle Gamma (z)}

. El contorno del módulo

{displaystyle SilencioGamma (z)

también se muestra.

Parcela tridimensional del valor absoluto de la compleja función gamma

El comportamiento de ${displaystyle Gamma (x)}$ para una variable real positiva creciente es dada por la fórmula de Stirling

{displaystyle Gamma (x+1)sim {2pi x}left({frac {x}{e}}right)}{x}}}}

donde el símbolo ${displaystyle sim }$ significa convergencia asintotica; la proporción de los dos lados converge a 1 en el límite ${textstyle xto +infty }$ . Este crecimiento es más rápido que exponencial, ${displaystyle exp(beta x)}$ , por cualquier valor fijo ${displaystyle beta }$ .

Otro límite útil para aproximaciones asintoticas ${displaystyle xto +infty }$ es:

{displaystyle {Gamma (x+alpha)}sim {Gamma (x)x^{alpha }},qquad alpha in mathbb {C}

Residuos

El comportamiento para no positivo ${displaystyle z}$ es más intrincado. La integral de Euler no converge para ${displaystyle Re (z)leq 0}$ , pero la función que define en el complejo positivo medio plano tiene una continuación analítica única al medio plano negativo. Una manera de encontrar que la continuación analítica es utilizar la integral de Euler para argumentos positivos y extender el dominio a números negativos mediante la aplicación repetida de la fórmula de recurrencia,

{displaystyle Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n)}}}}

elegir ${displaystyle n}$ tales que ${displaystyle z+n}$ es positivo. El producto en el denominador es cero cuando ${displaystyle z}$ equivale a cualquiera de los enteros ${displaystyle 0,-1,-2,ldots}$ . Así, la función gamma debe ser indefinida en esos puntos para evitar la división por cero; es una función meromorfa con postes simples en los enteros no positivos.

Para una función ${displaystyle f}$ de una variable compleja ${displaystyle z}$ , en un poste simple ${displaystyle c}$ , el residuo de ${displaystyle f}$ es dado por:

{displaystyle operatorname {Res} (f,c)=lim _{zto c}(z-c)f(z). }

Para el poste simple ${displaystyle z=-n,}$ reescribimos la fórmula de recurrencia como:

{displaystyle (z+n)Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n-1)}}}

El numerador a ${displaystyle z=-n,}$ es

{displaystyle Gamma (z+n+1)=Gamma (1)=1}

y el denominador

{displaystyle z(z+1)cdots (z+n-1)=-n(1-n)cdots (n-1-n)=(-1)^{n}n!.}

Entonces, los residuos de la función gamma en esos puntos son:

{displaystyle operatorname {Res} (Gamma-n)={frac {(-1)} {n}}}}}} {fn} {fn}} {fn}}} {fn}}} {fn}}}} {fn}}} {fn}}} {fn}}}}} {fnfnfnf}}}}}}}}}}}}}}}}}}} {\fnfnfnfnf}}}}}}}}} {f}} {\fnfnKfnfnKf}}}}}}}}}}}}}}}}}}}}}}} {\fn}}}}}}}}}}} {fn\\fn}}}}}}}}} {fnKfnKfnfnKfnKfnKf}}}}}}}

La función gamma no es cero en todas partes a lo largo de la línea real, aunque viene arbitrariamente cerca de cero como $z \to$ . De hecho, no hay número complejo ${displaystyle z}$ para la cual ${displaystyle Gamma (z)=0}$ , y por lo tanto la función gamma recíproca ${textstyle {frac {1}{Gamma (z)}}}$ es una función completa, con ceros a ${displaystyle z=0,-1,-2,ldots$ .

Mínimas y máximas

(feminine)

En la línea real, la función gamma tiene un mínimo local en $z min \approx +1.46163 214496836234126$ donde alcanza el valor $Γ(z min) \approx +0.88560 319441088870027$ . La función gamma se eleva a ambos lados de este mínimo. La solución a $Γ(z - 0.5) = Γ(z + 0.5)$ es $z = +1.5$ y el valor común es $Γ(1) = Γ(2) = +1$ . La solución positiva de $Γ(z - 1) = Γ(z + 1)$ es $z = φ \approx +1,618$ , la proporción áurea y el valor común es $Γ(φ - 1) = Γ(φ + 1) = φ! \approx +1.44922 960226989660037$ .

La función gamma debe alternar el signo entre sus polos en los enteros no positivos porque el producto en la recurrencia delantera contiene un número impar de factores negativos si el número de polos entre ${displaystyle z}$ y ${displaystyle z+n}$ es extraño, y un número incluso si el número de polos es incluso. Los valores extremos de la función Gamma entre los enteros no positivos son $. -0.50408 3008264549 38526...) -3.54464 3611155005 08912...$ , $. -1.57349 8473162390 45877...) 2.30240 7258339680 13582...$ , $. -2.61072 0868444144 65000...) -0.88813 6358401241 92009...$ , $. -3.63529 3366436901 09783...) 0.24512 7539834366 25043...$ , $. -4.65323 7761743142 44171...) -0.05277 9639587319 40076...$ , etc.

Representaciones integrales

Hay muchas fórmulas, además de la integral de Euler de segundo tipo, que expresan la función gamma como una integral. Por ejemplo, cuando la parte real de $z$ es positiva,

{displaystyle Gamma (z)=int _{-infty } {infty }e^{zt-e^{t},dt}

{displaystyle Gamma (z)=int ¿Qué?

Donde ${displaystyle log }$ denota el logaritmo complejo.

La primera fórmula integral de Binet para la función gamma establece que, cuando la parte real de $z$ es positiva, después:

{displaystyle log Gamma (z)=left(z-{frac {1}{2}right)log z-z+{frac {1}{2}ln(2pi)+int _{0}^{infty }left({frac {1}{2}-{frac} {1}{}+{frac} {1}{e^{t}}right){frac - ¿Qué?

La integral del lado derecho puede interpretarse como una transformada de Laplace. Es decir,

{displaystyle log left(Gamma (z)left({frac {e}{z}right)^{z}{sqrt {2pi z}right)={mathcal {L}left({fracfrac] {1}{2t}-{frac {1}{2}}}+{frac {1}{t(e^{t}}right)(z). }

La segunda fórmula integral de Binet establece que, de nuevo, cuando la parte real de $z$ es positiva, entonces:

{displaystyle log Gamma (z)=left(z-{frac {1}{2}right)log z-z+{frac {1}{2}ln(2pi)+2int _{0}^{infty }{frac {arctan(t/z)}{e^{2pi) - Sí.

Vamos $C$ ser un contorno de Hankel, que significa un camino que comienza y termina en el punto $JUEGO$ en la esfera Riemann, cuyo vector tangente unidad converge a $-1$ al inicio del camino y a $1$ al final, que tiene viento número 1 alrededor $0$ , y que no cruza $[0, \infty]$ . Arreglar una rama de ${displaystyle log(-t)}$ tomando una rama cortada $[0, \infty]$ y tomando ${displaystyle log(-t)}$ ser real cuando $t$ está en el eje real negativo. Assume $z$ no es un entero. Entonces la fórmula de Hankel para la función gamma es:

{displaystyle Gamma (z)=-{2isin pi z}int _{C}(-t)^{z-1}e^{-t},dt,}

Donde ${displaystyle (-t)^{z-1}$ se interpreta como ${displaystyle exp(z-1)log(-t)}$ . La fórmula de reflexión conduce a la expresión estrechamente relacionada

{fnMicroc} {1} {fnMicroc {fnK}int _{C}(-t)^{-z}e^{-t}

de nuevo válido siempre que $z$ no sea un número entero.

Representación de fracciones continuas

La función gamma también se puede representar mediante la suma de dos fracciones continuas:

{displaystyle Gamma (z)={cfrac {0}{2+0-z+1{cfrac {z-1}{2+2-z+2{cfrac {z-2}{2+4-z+3{cfrac {z-3}{2+6-z+4{cfrac {z-4}{2+8-z+5{cfrac {z-5}{2+10-z+ddots {}}}}}}}} {frac {cHFF}{z+0-{cfrac {z+0}{z+1+{cfrac {1}{z+2-{cfrac {z+1}{z+3+{cfrac {2}{z+4-{cfrac {z+2}{z+5+{cfrac {3}{z+6-ddots - Sí.

Donde ${displaystyle zin mathbb {C}$ .

Expansión de la serie Fourier

El logaritmo de la función gamma tiene la siguiente expansión de serie Fourier para ${displaystyle 0 segnunció1:}$

{fn} {fn}fnfn}fn}fnfn}nnnnnnnnc}nnnc} {fnfn} {fnfn}nccccH0}ccH0} {cH0} {ccH0}ccH0}c}cccccccccccccccccccccccccccH0}cH0}ccccccccccccc}cccccH0}ccccH0}cH0}cccH0}ccH0}ccccccc

que durante mucho tiempo se atribuyó a Ernst Kummer, quien la derivó en 1847. Sin embargo, Iaroslav Blagouchine descubrió que Carl Johan Malmsten derivó esta serie por primera vez en 1842.

Fórmula de Raabe

En 1840, Joseph Ludwig Raabe demostró que

{displaystyle int _{a+1}ln Gamma (z),dz={2}ln 2pi +aln a-a,quad a título0.}

En particular, si ${displaystyle a=0}$ entonces

{displaystyle int _{0}{1}ln Gamma (z),dz={tfrac {1}ln 2pi}

Este último se puede derivar tomando el logaritmo en la fórmula de multiplicación anterior, que da una expresión para la suma Riemann del integrado. Tomando el límite ${displaystyle ato infty}$ da la fórmula.

Función Pi

Una notación alternativa que fue introducida originalmente por Gauss es la ${displaystyle Pi }$ - Función, que, en términos de la función gamma, es

{displaystyle Pi (z)= Gamma (z+1)=z Gamma (z)=int ¿Qué?

así ${displaystyle Pi (n)=n!}$ para cada entero no negativo ${displaystyle n}$ .

Usando la función pi, la fórmula de reflexión toma la forma

{displaystyle Pi (z)Pi (-z)={frac {pi z}{sin(pi z)}}={frac {1}{operatorname {Sinc} (z)}}}

donde $sinc$ es la función sinc normalizada, mientras que el teorema de la multiplicación adopta la forma

{displaystyle Pi left({frac {z}{m}right),Pi left({frac {z-1}{m}right)cdots Pi left({frac {z-m+1}right)=(2pi)^{frac {m-1}{-z-{frac} {1} {2}}Pi (z)}

A veces también encontramos

{displaystyle pi (z)={frac {1}{Pi (z)}}}

que es una función completa, definida para cada número complejo, al igual que la función gamma recíproca. Que ${displaystyle pi (z)}$ es entera implica que no tiene polos, así que ${displaystyle Pi left(zright)}$ , como ${displaystyle Gamma left(zright)}$ No tiene ceros.

El volumen de un n-elipsoide con radios $r 1, \dots, r n$ se puede expresar como

{displaystyle V_{n}(r_{1},dotscr_{n}={frac {pi ^{frac {fn} {fn} {fn}} {fn}} {fn}} {fn}}} {\fn}} {fn}}} {fn}}} {fn}}}}} {f}}} {\fn}}}}} {\fn}}}}}} {\f}}}}}}}}}}}}}}}} {\\\\}}}}}}}}}}}}}}}} {\\\\\\\}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ Pi left ({frac {n}right)}prod ¿Qué?

Relación con otras funciones

En la primera parte superior, que define la función gamma, se fijan los límites de la integración. Las funciones de gamma incompleta superior e inferior son las funciones obtenidas permitiendo que el límite inferior o superior (respectivamente) de la integración varíe.
La función gamma está relacionada con la función beta por la fórmula ${displaystyle mathrm {B} (z_{1},z_{2}=int ¿Por qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} Gamma (z_{1}+z_{2}}}}}$
El derivado logarítmico de la función gamma se llama función digamma; los derivados superiores son las funciones de poligamma.
El análogo de la función gamma sobre un campo finito o un anillo finito son las sumas gaisianas, un tipo de suma exponencial.
La función gamma recíproca es toda una función y se ha estudiado como un tema específico.
La función gamma también aparece en una relación importante con la función Riemann zeta, ${displaystyle zeta (z)}$ . ${displaystyle pi ^{-{frac {Z}{2};; Gamma left({frac {z}{2}right)zeta (z)=pi ^{-{frac {1-z}{2}; Gamma left({frac {1-z}{2}right);zeta (1-z). }$ También aparece en la siguiente fórmula: ${displaystyle zeta (z)Gamma (z)=int ¿Qué?$ que es válido sólo para ${displaystyle Re (z)}$ .
El logaritmo de la función gamma satisface la siguiente fórmula debido a Lerch: ${displaystyle log Gamma (z)=zeta _{H}'(0,z)-zeta '(0),}$ Donde ${displaystyle zeta ¿Qué?$ es la función Hurwitz zeta, ${displaystyle zeta }$ es la función Riemann zeta y la primera ( $.$ ) denota diferenciación en la primera variable.
La función gamma está relacionada con la función exponencial estirada. Por ejemplo, los momentos de esa función son ${displaystyle langle tau ^{n}rangle equiv int _{0}^{infty }dt,t^{n-1},e^{-left({frac {t}{tau }right)^{beta {fn} {fn} {fnK}} {fn}} {fn}}} {fn}} {beta }Gamma left({n over beta }right). }$

Valores particulares

Incluyendo hasta los primeros 20 dígitos después del punto decimal, algunos valores particulares de la función gamma son:

{displaystyle {begin{rcccl}Gamma left(-{tfrac {3}{2}}right) Sentido = 'tfrac {4{sqrt {pi) }}{3} {3} {approx &+2.36327,18012,07354,70306\\\\Gamma left(-{tfrac {1}{2}derecha) diezm = 2{sqrt {pi } {pi } {approx '-3.54490,77018,11032,05459\\\\\\Gammaleft({tfrac {1}{2}}}derecho) {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}}} {fnMicrosoft Sans)}}}}}}} {fnMicros}}fnunció= {fnMicroc {\sqrt {\pH0}}fnMicrox > {2}{2} {0.88622,69254,52758\,01364\\\\\\\\\\\\\\Gamma}derecho)} {fnMicrosoft Sans Serif}} {fnMicroc {3}}}}}}}}dere) {4}} {4} {fnMicrox > 0,32934,03881,79137,02047\\\\\\\\\\\\\cH003nMicrosoft Sans Serif}} {fnMicroc {fnMicrosoft}}}}}}}}}}} {fnun}}}}}}}}}}} {m] {8}} {8} {3.32335,09704,47842,55118\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\cH001}}}}}}

(Consulte las secuencias A245886, A019707, A002161, A019704, A245884 y A245885 en el OEIS). La función gamma de valor complejo no está definida para enteros no positivos, pero en estos casos el valor se puede definir en la esfera de Riemann como $\infty$ . La función gamma recíproca está bien definida y es analítica en estos valores (y en todo el plano complejo):

{fnMicroc} {1} {fn}= {fnMicroc} {1}{Gamma (-2)}={frac {1}{Gamma (-1)}={frac {1}{Gamma (0)}}=0}

La función log-gamma

La función analítica

log z)

Debido a que las funciones gamma y factorial crecen tan rápidamente para argumentos moderadamente grandes, muchos entornos informáticos incluyen una función que devuelve el logaritmo natural de la función gamma (a menudo denominada lgamma o lngamma en entornos de programación o gammaln en hojas de cálculo); esto crece mucho más lentamente, y para cálculos combinatorios permite sumar y restar logaritmos en lugar de multiplicar y dividir valores muy grandes. A menudo se define como

{displaystyle ln Gamma (z)=-gamma z-ln z+sum _{k=1}{infty. {Z}{k}-ln left(1+{frac {z}right)right].}

La función digamma, que es la derivada de esta función, también se ve comúnmente. En el contexto de aplicaciones técnicas y físicas, p. con la propagación de la onda, la ecuación funcional

{displaystyle ln Gamma (z)=ln Gamma (z+1)-ln z}

Parcela de función gamma logarítmica en el plano complejo de -2-2i a 2+2i con colores creados con función Mathematica 13.1 ComplexPlot3D

se utiliza a menudo ya que permite determinar los valores de función en una tira de ancho 1 en $z$ de la franja vecina. En particular, comenzando con una buena aproximación para un $z$ con gran parte real uno puede ir paso a paso hacia abajo al deseado $z$ . Siguiendo una indicación de Carl Friedrich Gauss, Rocktaeschel (1922) propuesto para ${displaystyle ln(Gamma (z)}$ una aproximación para grande $Re(z)$ :

{displaystyle ln Gamma (z)approx (z-{tfrac {1}{2}})ln z-z+{tfrac {1}{2}ln(2pi).}

Esto se puede usar para aproximar con precisión $ln(Γ(z))$ para $z$ con una $Re(z)$ vía más pequeña (P.E.Böhmer, 1939)

{displaystyle ln Gamma (z-m)=ln Gamma (z)-sum _{k=1}^{m}ln(z-k). }

Se puede obtener una aproximación más precisa utilizando más términos de las expansiones asintóticas de $ln(Γ(z))$ y $Γ(z)$ , que se basan en la aproximación de Stirling.

{displaystyle Gamma (z)sim z^{z-{frac {1} {2}}}e^{-z}{sqrt {2pi}left(1+{frac}{sqrt {2pi}}}}left(1+{frac} {f} {f} {f} {f} {f} {f}} {f}f}}}}}f}}}}} {f}}} {f}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f}} {f}}}}}}}}}f}}}}}}}} {f} {f}} {f} {f} {f}}}}}} {f}}}}} {f} {f}f}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {1}{12z}+{frac} {1}{288z^{2}}}-{frac {139}{51,840z^{3}}-{frac {571}{2,488,320z^{4}}right)}

como

Silencio z Silencio \to

constante

Silencio arg(z) TENIDO ANTERIOR

. (Ver secuencias A001163 y A001164 en el OEIS.)

De una forma más "natural" presentación:

{displaystyle ln Gamma (z)=zln z-z-{tfrac {1}{2}ln Z+{tfrac {1}{2}ln 2pi} +{frac {1}{12z}-{frac} {1}{360z^{3}}}+{frac {1}{1260z^{5}}}+oleft({frac {1}{z^{5}}}right)}}}

como

Silencio z Silencio \to

constante

Silencio arg(z) TENIDO ANTERIOR

. (Ver secuencias A046968 y A046969 en el OEIS.)

Los coeficientes de los términos con $k > 1$ de $z 1- k$ en la última expansión son simplemente

{displaystyle {frac {fnK}{k(k-1)}}}

donde $B k$ son los números de Bernoulli.

La función Gamma también tiene la Serie de Stirling (derivada por Charles Hermite en 1900) igual a

{displaystyle log Gamma (1+x)={frac {x(x-1)}{2!}log(2)+{frac {x(x-1)(x-2)}{3!}(log(3)-2log(2))+cdotsquad Re (x) Conf0.}

Propiedades

El teorema de Bohr-Mollerup establece que entre todas las funciones que extienden las funciones factoriales a los números reales positivos, solo la función gamma es log-convexa, es decir, su logaritmo natural es convexo en el eje real positivo. Otra caracterización viene dada por el teorema de Wielandt.

En cierto sentido, la función $ln(Γ)$ es la forma más natural; hace que algunos atributos intrínsecos de la función sean más claros. Un ejemplo llamativo es la serie de Taylor de $ln(Γ)$ alrededor de 1:

{displaystyle ln Gamma (z+1)=-gamma z+sum _{k=2}^{infty }{frac {zeta (k)}{k},(-z)^{k}qquad forall ;

con $ζ (k)$ que denota la función zeta de Riemann en $k$ .

Entonces, usando la siguiente propiedad:

{displaystyle zeta (s)Gamma (s)=int _{0}{infty }{frac {t^{s}{e^{t}}}\fnMic {dt}{t}}

podemos encontrar una representación integral para la función $ln(Γ)$ :

{displaystyle ln Gamma (z+1)=-gamma ¿Por qué?

o, estableciendo $z = 1$ para obtener una integral para $γ < /span>, podemos reemplazar el término γ con su integral e incorporarlo en la fórmula anterior, para obtener:$

{displaystyle ln Gamma (z+1)=int ¿Por qué?

También existen fórmulas especiales para el logaritmo de la función gamma para racionalizar $z$ . Por ejemplo, si ${displaystyle k}$ y ${displaystyle n}$ son enteros con ${displaystyle k maden}$ y ${displaystyle kneq n/2,}$ entonces

{displaystyle {begin{aligned}ln} Gamma left({frac {n}right)={frac {,(n-2k)ln 2pi) ¿Qué? pi -ln sin {frac {pi k}n}, right}+{frac {1}{pi} {fnMicrosoft Sans Serif}}cdot sin {fn,2fnfn}cdot sin {fnfn,2fnfnMicroc} rk,} {n}\fn} {fnMicroc {1}{2pi}sin {frac} {2ccH00} {fn}cdot !int _{0}{infty }! {fnMic {,e^{-nx}!cdot ln x,}{,cosh x-cos(2pi k/n),},{m} {m} {fn} {fn}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}cdot}cdot}f}f}f}f}f}f}f}f}f}f}f}f}cdotfn}cdot}cdotcdotf}cdotf}fn}fnh}cdotcdot}fnh}f}cdot}cdotfn }xend{aligned}

ver. Esta fórmula a veces se usa para cálculos numéricos, ya que el integrando disminuye muy rápidamente.

Integración sobre log-gamma

La integral

{displaystyle int _{0}ln Gamma (x),dx}

se puede expresar en términos de la función G de Barnes (consulte la función G de Barnes para ver una prueba):

{displaystyle int ¿Qué? Gamma (x),dx={2}ln(2pi)+{frac {z(1-z)}{2}}+zln Gamma (z)-ln G(z+1)}

donde $Re(z) > -1$ .

También se puede escribir en términos de la función zeta de Hurwitz:

{displaystyle int ¿Qué? Gamma (x),dx={2}ln(2pi)+{frac {z(1-z)}{2}}-zeta '(-1)+zeta '(-1,z). }

Cuando ${displaystyle z=1}$ sigue que

{displaystyle int _{0}{1}ln Gamma (x),dx={2}ln(2pi),}

y esto es una consecuencia de la fórmula de Raabe también. O. Espinosa y V. Moll deriva una fórmula similar para la parte integral del cuadrado ${displaystyle ln Gamma }$ :

{displaystyle int _{0}ln ^{2}Gamma (x)dx={frac} {gamma} ¿Qué? # {2}{4}} {fnMic {1} {3} ¿Qué?

Donde ${displaystyle L_{1}$ es ${displaystyle {frac {2}ln(2pi)}$ .

D. H. Bailey y sus coautores dieron una evaluación para

{displaystyle ¿Qué?

cuando ${displaystyle n=1,2}$ en términos de la función Tornheim-Witten zeta y sus derivados.

Además, también se sabe que

{displaystyle lim _{nto infty}{frac {L_{n} {n}}=1.}

Aproximaciones

Gama de comparación (línea azul) con el factorial (puntos azules) y la aproximación de Stirling (línea roja)

Los valores complejos de la función gamma se pueden aproximar usando la aproximación de Stirling o la aproximación de Lanczos,

{displaystyle Gamma (z)sim {2sqrt}z^{z-1/2}e^{-z}quad {hbox{as }}zto infty { in }left durablearg(z)right sobre la vida recomendadapi.}

Esto es preciso en el sentido de que la proporción de la aproximación al valor real se aproxima a 1 en el límite como $| z |$ va hasta el infinito.

La función gamma se puede calcular a precisión fija para ${displaystyle operatorname {Re} (z)in [1,2]}$ aplicando la integración por partes a la integral de Euler. Para cualquier número positivo $x$ la función gamma se puede escribir

{displaystyle {begin{aligned} Gamma (z) ¿Qué? {dt}{t}+int ¿Qué? {T}fn}\\cH00cH00}fn9}s}s}s} ¿Por qué? {dt} {dt}}.end{aligned}}

Cuando $Re(z).$ y ${displaystyle xgeq 1}$ , el valor absoluto de la última integral es menor que ${displaystyle (x+1)e^{-x}$ . Eligiendo un lo suficientemente grande ${displaystyle x}$ , esta última expresión se puede hacer más pequeña que ${displaystyle 2^{-N}$ para cualquier valor deseado ${displaystyle N}$ . Así, la función gamma se puede evaluar para ${displaystyle N}$ bits de precisión con la serie anterior.

E.A. construyó un algoritmo rápido para el cálculo de la función gamma de Euler para cualquier argumento algebraico (incluido el racional). Karatsuba.

Para argumentos que son múltiplos enteros de $1 / 24$ , la función gamma también se puede evaluar rápidamente usando iteraciones de media aritmética-geométrica (ver valores particulares de la función gamma).

Aplicaciones

Un autor describe la función gamma como "Posiblemente, la función especial más común, o la menos 'especial' de ellos. Las otras funciones trascendentales […] se denominan 'especiales' porque posiblemente podría evitar algunos de ellos al mantenerse alejado de muchos temas matemáticos especializados. Por otro lado, la función gamma $Γ(z)$ es la más difícil de evitar."

Problemas de integración

La función gamma encuentra aplicación en áreas tan diversas como la física cuántica, la astrofísica y la dinámica de fluidos. La distribución gamma, que se formula en términos de la función gamma, se utiliza en estadística para modelar una amplia gama de procesos; por ejemplo, el tiempo entre ocurrencias de terremotos.

La razón principal de la utilidad de la función gamma en tales contextos es la prevalencia de expresiones del tipo ${displaystyle f(t)e^{-g(t)}$ que describen procesos que se descomponen exponencialmente en tiempo o espacio. Los integrales de tales expresiones pueden resolverse ocasionalmente en términos de la función gamma cuando no existe una solución elemental. Por ejemplo, si $f$ es una función de potencia y $g$ es una función lineal, un simple cambio de variables da la evaluación

{displaystyle int _{0}{infty }t^{b}e^{-at},dt={frac {1}{a^{b}} {}} {}} {f}} {f}}}} ¿Qué? {Gamma (b+1)}{a^{b+1}}}

El hecho de que la integración se realice a lo largo de toda la línea real positiva podría significar que la función gamma describe la acumulación de un proceso dependiente del tiempo que continúa indefinidamente, o el valor podría ser el total de una distribución en un espacio infinito.

Por supuesto, con frecuencia es útil tomar límites de integración distintos de 0 y $\infty$ para describir la acumulación de un proceso finito, en cuyo caso la función gamma ordinaria ya no es una solución; la solución se llama entonces función gamma incompleta. (La función gamma ordinaria, obtenida mediante la integración a lo largo de toda la línea real positiva, a veces se denomina función gamma completa por contraste).

Una categoría importante de funciones que decaen exponencialmente es la de las funciones gaussianas

{fnMicrosoft Sans Serif}}}

e integrales, como la función de error. Hay muchas interrelaciones entre estas funciones y la función gamma; en particular, el factor ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\fn }$ obtenido mediante evaluación ${textstyle Gamma left({frac {1}right)}$ es el "iguo" que se encuentra en el factor normalizador de la función de error y la distribución normal.

Las integrales que hemos discutido hasta ahora involucran funciones trascendentales, pero la función gamma también surge de integrales de funciones puramente algebraicas. En particular, las longitudes de arco de las elipses y de la lemniscata, que son curvas definidas por ecuaciones algebraicas, vienen dadas por integrales elípticas que en casos especiales pueden evaluarse en términos de la función gamma. La función gamma también se puede utilizar para calcular el "volumen" y "área" de hiperesferas $n$ -dimensionales.

Cálculo de productos

La capacidad de la función gamma para generalizar productos factoriales lleva inmediatamente a aplicaciones en muchas áreas de las matemáticas; en combinatoria, y por extensión en áreas como la teoría de probabilidades y el cálculo de series de potencias. Muchas expresiones que involucran productos de enteros sucesivos se pueden escribir como una combinación de factoriales, siendo quizás el ejemplo más importante el del coeficiente binomial

{displaystyle {binom {fn}={frac} ¡No!

El ejemplo de los coeficientes binomiales explica por qué las propiedades de la función gamma cuando se extienden a números negativos son naturales. Un coeficiente binomial proporciona el número de formas de elegir $k$ elementos de un conjunto de $n$ elementos; si $k > n$ , por supuesto que no hay manera. Si $k > n$ , $(n - k)!$ es el factorial de un entero negativo y, por lo tanto, infinito si usamos la definición de función gamma de factoriales: dividir por infinito da el valor esperado de 0.

Podemos reemplazar el factorial por una función gamma para extender cualquier fórmula de este tipo a los números complejos. En general, esto funciona para cualquier producto en el que cada factor sea una función racional de la variable índice, al factorizar la función racional en expresiones lineales. Si $P$ y $Q$ son polinomios mónicos de grado $m$ y $n$ con raíces respectivas < abarcan clase="texhtml">p₁, …, p_m y q₁, …, q_n, tenemos

{displaystyle prod _{i=a}{b}{frac {P(i)}{Q(i)}}=left(prod) - ¿Qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}}}}}} {\\\fn\fnMicrob}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn\fn\\\fn\cHcHcHcHcHcHcHcHcHcHcH Gamma (a-p_{j}}}right)left(prod ¿Qué? {Gamma (a-q_{k}}}}derecha). }

Si tenemos una forma de calcular numéricamente la función gamma, es muy fácil calcular los valores numéricos de dichos productos. El número de funciones gamma en el lado derecho depende únicamente del grado de los polinomios, por lo que no importa si $b - a$ es igual a 5 o 10⁵. Al tomar los límites apropiados, también se puede hacer que la ecuación se mantenga incluso cuando el producto de la izquierda contiene ceros o polos.

Al tomar límites, ciertos productos racionales con infinitos factores también pueden evaluarse en términos de la función gamma. Debido al teorema de factorización de Weierstrass, las funciones analíticas se pueden escribir como productos infinitos y, a veces, se pueden representar como productos finitos o cocientes de la función gamma. Ya hemos visto un ejemplo sorprendente: la fórmula de reflexión representa esencialmente la función seno como el producto de dos funciones gamma. Partiendo de esta fórmula, tanto la función exponencial como todas las funciones trigonométricas e hiperbólicas se pueden expresar en términos de la función gamma.

Aún se pueden representar más funciones, incluida la función hipergeométrica y sus casos especiales, mediante integrales de contorno complejas de productos y cocientes de la función gamma, denominadas integrales de Mellin-Barnes.

Teoría analítica de números

Una aplicación de la función gamma es el estudio de la función zeta de Riemann. Una propiedad fundamental de la función zeta de Riemann es su ecuación funcional:

{displaystyle Gamma left({frac {s}right)zeta (s)pi ^{-{frac {frac}}right)zeta (s)pi ^{-{frac} {fnMicrosoft}}=fnMicrosoft} Gamma left({frac {1-s}{2}right)zeta (1-s)pi ^{-{frac {1-s}{2}}}}

Entre otras cosas, esto proporciona una forma explícita para la continuación analítica de la función zeta a una función meromórfica en el plano complejo y conduce a una prueba inmediata de que la función zeta tiene infinitas funciones llamadas "triviales&#. 34; ceros en la recta real. Borwein et al. llaman a esta fórmula "uno de los descubrimientos más bellos de las matemáticas". Otro contendiente por ese título podría ser

{displaystyle zeta (s);Gamma (s)=int _{0}{infty }{frac {t^{s}{e^{t}}},{frac.

Ambas fórmulas fueron derivadas por Bernhard Riemann en su artículo seminal de 1859 "Ueber die Anzahl der Primzahlen unter einer gegebenen Größe" ("Sobre el número de primos menores que una magnitud dada"), uno de los hitos en el desarrollo de la teoría analítica de números, la rama de las matemáticas que estudia los números primos utilizando las herramientas del análisis matemático. Los números factoriales, considerados como objetos discretos, son un concepto importante en la teoría clásica de números porque contienen muchos factores primos, pero Riemann encontró un uso para su extensión continua que podría decirse que resultó ser aún más importante.

Historia

La función gamma ha captado el interés de algunos de los matemáticos más destacados de todos los tiempos. Su historia, especialmente documentada por Philip J. Davis en un artículo que le valió el premio Chauvenet en 1963, refleja muchos de los principales avances en las matemáticas desde el siglo XVIII. En palabras de Davis, "cada generación ha encontrado algo interesante que decir sobre la función gamma. Quizás la próxima generación también lo haga."

Siglo XVIII: Euler y Stirling

Carta de Daniel Bernoulli a Christian Goldbach, 6 de octubre de 1729

El problema de extender el factorial a argumentos no enteros aparentemente fue considerado por primera vez por Daniel Bernoulli y Christian Goldbach en la década de 1720. En particular, en una carta de Bernoulli a Goldbach del 6 de octubre de 1729, Bernoulli introdujo la representación del producto

{displaystyle x!=lim _{nto infty }left(n+1+{frac {x}{2}right)}{x-1}prod ¿Qué? {k+1}{k+x}}

x

Leonard Euler luego dio dos definiciones diferentes: la primera no era su integral sino un producto infinito que está bien definido para todos los números complejos $n$ otra que los enteros negativos,

{displaystyle n!=prod _{k=1}}{infty }{frac {left(1+{frac {1}{k}}right)}{n}{1+{frac}{frac} {fn}{fn}{f}}}{n}}{1+{f}{,

De lo cual informó a Goldbach en una carta fechada el 13 de octubre de 1729. Volvió a escribir a Goldbach el 8 de enero de 1730 para anunciarle su descubrimiento de la representación integral.

{displaystyle n!=int _{0} {ln s)},ds,}

que es válido cuando la parte real del número complejo $n$ es estrictamente mayor que $-1$ (es decir, ${displaystyle Re (n) confianza-1}$ ). Por el cambio de variables $t = s$ , esto se convierte en la familiar integral Euler. Euler publicó sus resultados en el documento "De progressionibus transcendentibus seu quarum termini general algebraice dari nequeunt" ("Sobre progresiones trascendentales, es decir, aquellos cuyos términos generales no se pueden dar algebraicamente"), presentado a la Academia de San Petersburgo el 28 de noviembre de 1729. Euler descubrió algunas de las propiedades funcionales importantes de la función gamma, incluyendo la fórmula de reflexión.

James Stirling, un contemporáneo de Euler, también intentó encontrar una expresión continua para el factorial e ideó lo que ahora se conoce como la fórmula de Stirling. Aunque la fórmula de Stirling da una buena estimación de $n!$ , también para números no enteros, no proporciona el valor exacto. Las extensiones de su fórmula que corrigen el error fueron dadas por el propio Stirling y por Jacques Philippe Marie Binet.

Siglo XIX: Gauss, Weierstrass y Legendre

La primera página del periódico de Euler

Carl Friedrich Gauss reescribió el producto de Euler como

{displaystyle Gamma (z)=lim _{mto infty }{frac {m^{z}m!}{z(z+1)cdots (z+m)}}}}}

y usé esta fórmula para descubrir nuevas propiedades de la función gamma. Aunque Euler fue un pionero en la teoría de variables complejas, no parece haber considerado el factorial de un número complejo, como lo hizo Gauss por primera vez. Gauss también demostró el teorema de la multiplicación de la función gamma e investigó la conexión entre la función gamma y las integrales elípticas.

Karl Weierstrass estableció aún más el papel de la función gamma en el análisis complejo, a partir de otra representación del producto,

{displaystyle Gamma (z)={frac {e^{-gamma } {z}prod ¿Por qué? {Z} {k}right)}{-1}e^{frac} {Z}{k},}

donde $γ$ es la constante de Euler-Mascheroni. Weierstrass originalmente escribió su producto como uno para $1 / Γ$ , en cuyo caso se toma los ceros de la función en lugar de sus polos. Inspirado por este resultado, demostró lo que se conoce como el teorema de factorización de Weierstrass: que cualquier función completa puede escribirse como un producto sobre sus ceros en el plano complejo; una generalización del teorema fundamental del álgebra.

El nombre función gamma y el símbolo $Γ$ fueron introducidos por Adrien-Marie Legendre alrededor de 1811; Legendre también reescribió la definición integral de Euler en su forma moderna. Aunque el símbolo es una gamma griega mayúscula, no existe un estándar aceptado sobre si el nombre de la función debe escribirse "función gamma" o "Función gamma" (Algunos autores simplemente escriben " $Γ$ -función"). La "función pi" alternativa notación $Π(z) = z!$ debida a Gauss a veces se encuentra en la literatura más antigua, pero Legendre's la notación es dominante en las obras modernas.

Se justifica preguntar por qué distinguemos entre el "factorial ordinario" y la función gamma utilizando símbolos distintos, y en particular por qué la función gamma debe ser normalizada para $. n + 1) n!$ en lugar de simplemente usar " $. n) n!$ ". Considere que la notación para los exponentes, $x n$ , se ha generalizado de números enteros a números complejos $x z$ sin ningún cambio. La motivación de Legendre para la normalización no parece ser conocida, y ha sido criticada como engorrosa por algunos (el matemático del siglo XX Cornelius Lanczos, por ejemplo, lo llamó "voide de cualquier racionalidad" y en cambio usaría $z!$ ). La normalización de Legendre simplifica algunas fórmulas, pero complica a otros. Desde un punto de vista moderno, la normalización Legendre de la función Gamma es la parte integral del carácter aditivo $e - x$ contra el carácter multiplicativo $x z$ con respecto a la medida de Haar ${textstyle {frac {dx}{x}}}$ en el grupo Lie $R +$ . Así, esta normalización hace más claro que la función gamma es un análogo continuo de una suma Gauss.

Siglos XIX y XX: caracterización de la función gamma

Es algo problemático que se haya dado una gran cantidad de definiciones para la función gamma. Aunque describen la misma función, no es del todo sencillo probar la equivalencia. Stirling nunca probó que su fórmula extendida corresponda exactamente a la función gamma de Euler; Charles Hermite dio por primera vez una prueba en 1900. En lugar de encontrar una prueba especializada para cada fórmula, sería deseable tener un método general para identificar la función gamma.

Una forma de demostrarlo sería encontrar una ecuación diferencial que caracterice la función gamma. La mayoría de las funciones especiales en matemáticas aplicadas surgen como soluciones a ecuaciones diferenciales, cuyas soluciones son únicas. Sin embargo, la función gamma no parece satisfacer ninguna ecuación diferencial simple. Otto Hölder demostró en 1887 que la función gamma al menos no satisface ninguna ecuación diferencial algebraica al mostrar que una solución a tal ecuación no podría satisfacer la fórmula de recurrencia de la función gamma, convirtiéndola en una función trascendentalmente trascendental. Este resultado se conoce como teorema de Hölder.

No se proporcionó una caracterización definitiva y de aplicación general de la función gamma hasta 1922. Harald Bohr y Johannes Mollerup demostraron entonces lo que se conoce como el teorema de Bohr-Mollerup: que la función gamma es la única solución a la relación de recurrencia factorial que es positiva y logarítmicamente convexa para $z$ positivo y cuyo valor es 1 es 1 (una función es logarítmicamente convexa si su logaritmo es convexo). Otra caracterización viene dada por el teorema de Wielandt.

El teorema de Bohr-Mollerup es útil porque es relativamente fácil probar la convexidad logarítmica para cualquiera de las diferentes fórmulas utilizadas para definir la función gamma. Yendo más allá, en lugar de definir la función gamma mediante una fórmula en particular, podemos elegir las condiciones del teorema de Bohr-Mollerup como definición y luego elegir cualquier fórmula que nos guste que satisfaga las condiciones como punto de partida para estudiar la función gamma.. Este enfoque fue utilizado por el grupo Bourbaki.

Borwein & Corless revisa tres siglos de trabajo sobre la función gamma.

Tablas de referencia y software

Aunque la función gamma se puede calcular prácticamente con la misma facilidad que cualquier función matemáticamente más simple con una computadora moderna, incluso con una calculadora de bolsillo programable, por supuesto, no siempre fue así. Hasta mediados del siglo XX, los matemáticos se basaban en tablas hechas a mano; en el caso de la función gamma, en particular una tabla calculada por Gauss en 1813 y otra calculada por Legendre en 1825.

Un gráfico dibujado a mano del valor absoluto de la función gamma compleja, desde Cuadros de funciones superiores por Jahnke y Emde[de].

Tablas de valores complejos de la función gamma, así como gráficos dibujados a mano, se proporcionaron en Tablas de funciones con fórmulas y curvas de Jahnke y Emde [de], publicado por primera vez en Alemania en 1909. Según Michael Berry, "la publicación en J&E de un El gráfico dimensional que muestra los polos de la función gamma en el plano complejo adquirió un estatus casi icónico."

De hecho, había poca necesidad práctica de algo más que valores reales de la función gamma hasta la década de 1930, cuando se descubrieron aplicaciones para la función gamma compleja en la física teórica. A medida que las computadoras electrónicas estuvieron disponibles para la producción de tablas en la década de 1950, se publicaron varias tablas extensas para la función gamma compleja para satisfacer la demanda, incluida una tabla con una precisión de 12 decimales de la Oficina Nacional de Normas de EE. UU.

Las implementaciones de punto flotante de precisión doble de la función gamma y su logaritmo ahora están disponibles en la mayoría de los programas informáticos científicos y las bibliotecas de funciones especiales, por ejemplo, TK Solver, Matlab, GNU Octave y GNU Scientific Library. La función gamma también se agregó a la biblioteca estándar de C (math.h). Las implementaciones de precisión arbitraria están disponibles en la mayoría de los sistemas de álgebra computacional, como Mathematica y Maple. PARI/GP, MPFR y MPFUN contienen implementaciones gratuitas de precisión arbitraria. La función factorial de la Calculadora de Windows devuelve Γ(x+1) cuando la entrada x no es un valor entero.

Contenido relacionado

Más resultados...

Función gamma

Motivación

Definición

Definición principal

Definiciones alternativas

La definición de Euler como producto infinito

Definición de Weierstrass

Propiedades

Generales

Desigualdades

Fórmula de Stirling

Residuos

Mínimas y máximas

Representaciones integrales

Representación de fracciones continuas

Expansión de la serie Fourier

Fórmula de Raabe

Función Pi

Relación con otras funciones

Valores particulares

La función log-gamma

Propiedades

Integración sobre log-gamma

Aproximaciones

Aplicaciones

Problemas de integración

Cálculo de productos

Teoría analítica de números

Historia

Siglo XVIII: Euler y Stirling

Siglo XIX: Gauss, Weierstrass y Legendre

Siglos XIX y XX: caracterización de la función gamma

Tablas de referencia y software

Contenido relacionado

WT Tutte

Grupo galois

Asociación Actuarial Internacional