Función descriptiva

En la teoría de sistemas de control, el método de la función descriptiva (DF), desarrollado por Nikolay Mitrofanovich Krylov y Nikolay Bogoliubov en la década de 1930, y ampliado por Ralph Kochenburger, es un procedimiento aproximado para analizar ciertos problemas de control no lineales. . Se basa en la cuasilinealización, que es la aproximación del sistema no lineal bajo investigación mediante una función de transferencia lineal invariante en el tiempo (LTI) que depende de la amplitud de la forma de onda de entrada. Por definición, una función de transferencia de un sistema LTI verdadero no puede depender de la amplitud de la función de entrada porque un sistema LTI es lineal. Por tanto, esta dependencia de la amplitud genera una familia de sistemas lineales que se combinan en un intento de capturar características destacadas del comportamiento del sistema no lineal. La función de descripción es uno de los pocos métodos ampliamente aplicables para diseñar sistemas no lineales y se usa ampliamente como herramienta matemática estándar para analizar ciclos límite en controladores de circuito cerrado, como controles de procesos industriales, servomecanismos y osciladores electrónicos.

El método

Considere la retroalimentación en torno a una no linealidad discontinua (pero continua por partes) (por ejemplo, un amplificador con saturación o un elemento con efectos de banda muerta) en cascada con un sistema lineal lento y estable. La región continua en la que se presenta la retroalimentación a la no linealidad depende de la amplitud de la salida del sistema lineal. A medida que la amplitud de salida del sistema lineal decae, la no linealidad puede moverse a una región continua diferente. Este cambio de una región continua a otra puede generar oscilaciones periódicas. El método de la función descriptiva intenta predecir las características de esas oscilaciones (por ejemplo, su frecuencia fundamental) asumiendo que el sistema lento actúa como un filtro de paso bajo o de paso de banda que concentra toda la energía alrededor de una sola frecuencia. Incluso si la forma de onda de salida tiene varios modos, el método aún puede proporcionar intuición sobre propiedades como la frecuencia y posiblemente la amplitud; En este caso, se puede considerar que el método de función descriptiva describe el modo deslizante del sistema de retroalimentación.

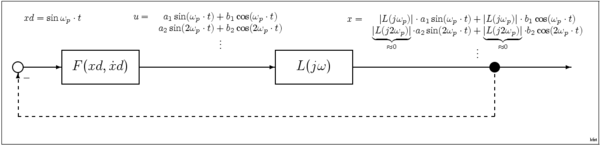
Utilizando esta suposición de baja velocidad, la respuesta del sistema puede ser descrita por una familia de formas de onda sinusoidales; en este caso el sistema se caracterizaría por una función de descripción de la entrada sine (SIDF) ${\displaystyle H(A,\,j\omega)}$ dar respuesta al sistema a una entrada consistente en una onda sine de amplitud A y frecuencia ${\displaystyle \omega }$. Este SIDF es una modificación de la función de transferencia ${\displaystyle H(j\omega)}$ utilizado para caracterizar sistemas lineales. En un sistema cuasi lineal, cuando la entrada es una onda sine, la salida será una onda sine de la misma frecuencia, pero con una amplitud escalada y fase desplazada como dada por ${\displaystyle H(A,\,j\omega)}$. Muchos sistemas son aproximadamente cuasi-linear en el sentido de que aunque la respuesta a una onda sine no es una onda de seno pura, la mayoría de la energía en la salida es de hecho a la misma frecuencia ${\displaystyle \omega }$ como la entrada. Esto se debe a que tales sistemas pueden poseer características intrínsecas de bajo paso o bandpass tales que los armónicos son naturalmente atenuados, o porque los filtros externos se agregan para este propósito. Una aplicación importante de la técnica SIDF es estimar la amplitud de oscilación en los osciladores electrónicos sinusoidales.

Otros tipos de funciones de descripción que se han utilizado son los DF para entradas de nivel y para entradas de ruido gaussiano. Aunque no son una descripción completa del sistema, los DF suelen ser suficientes para responder preguntas específicas sobre control y estabilidad. Los métodos DF son mejores para analizar sistemas con no linealidades relativamente débiles. Además, las funciones de descripción de entradas sinusoidales de orden superior (HOSIDF) describen la respuesta de una clase de sistemas no lineales a armónicos de la frecuencia de entrada de una entrada sinusoidal. Los HOSIDF son una extensión del SIDF para sistemas donde las no linealidades son significativas en la respuesta.

Advertencias

Aunque el método de función descriptiva puede producir resultados razonablemente precisos para una amplia clase de sistemas, puede fallar gravemente en otros. Por ejemplo, el método puede fallar si el sistema enfatiza los armónicos más altos de la no linealidad. Tzypkin ha presentado ejemplos de este tipo para sistemas bang-bang. Un ejemplo bastante similar es un oscilador de bucle cerrado que consta de un disparador Schmitt no inversor seguido de un integrador inversor que retroalimenta su salida a la entrada del disparador Schmitt. La salida del disparador Schmitt será una forma de onda cuadrada, mientras que la del integrador (que le sigue) tendrá una forma de onda triangular con picos que coincidirán con las transiciones en la onda cuadrada. Cada una de estas dos etapas del oscilador retrasa la señal exactamente 90 grados (en relación con su entrada). Si se realizara un análisis DF en este circuito, la onda triangular en la entrada del disparador Schmitt sería reemplazada por su fundamental (onda sinusoidal), que al pasar a través del disparador causaría un cambio de fase de menos de 90 grados ( porque la onda sinusoidal lo activaría antes que la onda triangular), por lo que parecería que el sistema no oscila de la misma manera (simple).

Además, en el caso de que se cumplan las condiciones de las conjeturas de Aizerman o Kalman, no existen soluciones periódicas mediante el método de la función descriptiva, pero se conocen contraejemplos con atractores periódicos ocultos. Se pueden construir contraejemplos del método de la función descriptiva para sistemas dinámicos discontinuos cuando un segmento en reposo destruye los ciclos límite predichos. Por lo tanto, la aplicación del método de la función descriptiva requiere una justificación adicional.