Función del trabajo
En física del estado sólido, la función de trabajo (a veces deletreada función de trabajo) es el trabajo termodinámico mínimo (es decir, energía) necesario para extraer un electrón de un sólido para un punto en el vacío inmediatamente fuera de la superficie sólida. Aquí "inmediatamente" significa que la posición final del electrón está lejos de la superficie en la escala atómica, pero todavía demasiado cerca del sólido para ser influenciada por los campos eléctricos ambientales en el vacío. La función de trabajo no es una característica de un material a granel, sino una propiedad de la superficie del material (dependiendo de la cara del cristal y la contaminación).
Definición
La función de trabajo W para una superficie dada se define por la diferencia
- W=− − eφ φ − − EF,{displaystyle ¿Qué?
donde −e es la carga de un electrón, ϕ es el potencial electrostático en el vacío cerca de la superficie, y EF es el nivel de Fermi (potencial electroquímico de electrones) dentro del material. El término −eϕ es la energía de un electrón en reposo en el vacío cerca de la superficie.
En la práctica, uno controla directamente EF por el voltaje aplicado al material a través de electrodos, y el trabajo la función es generalmente una característica fija del material de la superficie. En consecuencia, esto significa que cuando se aplica un voltaje a un material, el potencial electrostático ϕ producido en el vacío será algo menor que el voltaje aplicado, la diferencia depende de la función de trabajo de la superficie del material. Reordenando la ecuación anterior, se tiene
- φ φ =V− − We{displaystyle phi =V-{frac {W} {e}}
donde V = −EF/e es el voltaje del material (medido por un voltímetro, a través de un electrodo adjunto), en relación con una tierra eléctrica que se define como que tiene un nivel de Fermi cero. El hecho de que ϕ dependa de la superficie del material significa que el espacio entre dos conductores diferentes tendrá un campo eléctrico incorporado, cuando esos conductores están en equilibrio total entre sí (cortocircuitados eléctricamente entre sí y con temperaturas iguales).
La función de trabajo se refiere a la eliminación de un electrón a una posición lo suficientemente alejada de la superficie (muchos nm) como para que la fuerza entre el electrón y su imagen de carga en la superficie pueda despreciarse. El electrón también debe estar cerca de la superficie en comparación con el borde más cercano de una faceta de cristal o cualquier otro cambio en la estructura de la superficie, como un cambio en la composición del material, el revestimiento de la superficie o la reconstrucción. El campo eléctrico incorporado que resulta de estas estructuras, y cualquier otro campo eléctrico ambiental presente en el vacío, se excluyen al definir la función de trabajo.
Aplicaciones
- Emisión termonica
- En las pistolas de electrones termonicos, la función de trabajo y la temperatura de la cátodo caliente son parámetros críticos para determinar la cantidad de corriente que se puede emitir. El tungsteno, la opción común para los filamentos de tubo de vacío, puede sobrevivir a altas temperaturas pero su emisión es algo limitada debido a su función de trabajo relativamente alta (aproximadamente 4.5 eV). Al recubrir el tungsteno con una sustancia de la función de trabajo inferior (por ejemplo, torio o óxido de bario), la emisión puede aumentarse considerablemente. Esto prolonga la vida útil del filamento permitiendo la operación a temperaturas más bajas (para más información, vea cacao caliente).
- Modelos de flexión de banda en electrónica de estado sólido
- El comportamiento de un dispositivo de estado sólido depende en gran medida del tamaño de varias barreras Schottky y offsets de banda en las uniones de diferentes materiales, tales como metales, semiconductores y aisladores. Algunos enfoques heurísticos usados comúnmente para predecir la alineación de banda entre materiales, como la regla de Anderson y la regla Schottky-Mott, se basan en el experimento de pensamiento de dos materiales que se juntan en vacío, de tal manera que las superficies cobran y ajustan sus funciones de trabajo para llegar a ser iguales justo antes del contacto. En realidad estas funciones heurísticas son inexactas debido a su abandono de numerosos efectos microscópicos. Sin embargo, proporcionan una estimación conveniente hasta que el valor verdadero puede ser determinado por experimento.
- Equilibrio campos eléctricos en cámaras de vacío
- La variación en la función de trabajo entre diferentes superficies provoca un potencial electrostático no uniforme en el vacío. Incluso en una superficie ostensiblemente uniforme, variaciones en W conocidos como potenciales de parche están siempre presentes debido a inhomogeneidades microscópicas. Los potenciales de parche han interrumpido aparatos sensibles que dependen de un vacío perfectamente uniforme, como los experimentos de fuerza Casimir y el experimento Gravity Probe B. El aparato crítico puede tener superficies cubiertas con molibdeno, lo que muestra bajas variaciones en la función de trabajo entre diferentes caras de cristal.
- electrificación de contacto
- Si dos superficies conductoras se mueven en relación entre sí, y hay una diferencia potencial en el espacio entre ellas, entonces una corriente eléctrica será impulsada. Esto se debe a que la carga superficial de un conductor depende de la magnitud del campo eléctrico, que a su vez depende de la distancia entre las superficies. Los efectos eléctricos observados externamente son mayores cuando los conductores se separan por la distancia más pequeña sin tocar (una vez que entran en contacto, la carga fluirá internamente a través de la unión entre los conductores). Dado que dos conductores en equilibrio pueden tener una diferencia potencial incorporada debido a las diferencias de función de trabajo, esto significa que traer conductores desimilares en contacto, o desmontarlos, impulsará las corrientes eléctricas. Estas corrientes de contacto pueden dañar los circuitos microelectrónicos sensibles y ocurrir incluso cuando los conductores serían castigados en ausencia de movimiento.
Medición
Ciertos fenómenos físicos son muy sensibles al valor de la función de trabajo. Los datos observados de estos efectos se pueden ajustar a modelos teóricos simplificados, lo que permite extraer un valor de la función de trabajo. Estas funciones de trabajo extraídas fenomenológicamente pueden ser ligeramente diferentes de la definición termodinámica dada anteriormente. Para superficies no homogéneas, la función de trabajo varía de un lugar a otro, y diferentes métodos producirán diferentes valores de la típica "función de trabajo" ya que promedian o seleccionan de manera diferente entre las funciones de trabajo microscópicas.
Se han desarrollado muchas técnicas basadas en diferentes efectos físicos para medir la función de trabajo electrónico de una muestra. Se puede distinguir entre dos grupos de métodos experimentales para medir funciones de trabajo: absolutos y relativos.
- Los métodos absolutos emplean la emisión de electrones de la muestra inducida por la absorción de fotones (fotoemisión), por alta temperatura (emisión termonica), debido a un campo eléctrico (emisión de electrones de campo), o mediante el túnel de electrones.
- Los métodos relativos hacen uso de la diferencia potencial de contacto entre la muestra y un electrodo de referencia. Experimentalmente, se utiliza una corriente de ánodo de un diodo o la corriente de desplazamiento entre la muestra y la referencia, creada por un cambio artificial en la capacitancia entre los dos, se mide (el método Kelvin Probe, microscopio de fuerza de probe Kelvin). Sin embargo, los valores absolutos de la función de trabajo se pueden obtener si la punta se calibra primero en una muestra de referencia.
Métodos basados en emisión termoiónica
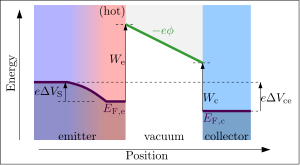
La función de trabajo es importante en la teoría de la emisión termoiónica, donde las fluctuaciones térmicas proporcionan suficiente energía para "evaporar" electrones de un material caliente (llamado "emisor") en el vacío. Si estos electrones son absorbidos por otro material más frío (llamado colector), entonces se observará una corriente eléctrica medible. La emisión termoiónica se puede utilizar para medir la función de trabajo tanto del emisor caliente como del colector frío. Generalmente, estas medidas implican ajustarse a la ley de Richardson, por lo que deben llevarse a cabo en un régimen de baja temperatura y baja corriente donde los efectos de carga espacial están ausentes.
Para pasar del emisor caliente al vacío, la energía de un electrón debe superar el nivel de Fermi del emisor en una cantidad
- Ebarrier=We{displaystyle E_{rm {}}=W_{rm {}} {fn}} {fn}} {fn}}}} {fn}} {fn}}} {fn}}}}}}}}}} {fn}}}}}}}}}}}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}}}} {
determinado simplemente por la función de trabajo termoiónico del emisor. Si se aplica un campo eléctrico hacia la superficie del emisor, todos los electrones que escapan serán acelerados lejos del emisor y absorbidos por cualquier material que esté aplicando el campo eléctrico. De acuerdo con la ley de Richardson, la densidad de corriente emitida (por unidad de área del emisor), Je (A/m2), está relacionado con la temperatura absoluta Te del emisor por la ecuación:
- Je=− − AeTe2e− − Ebarrier/kTe{displaystyle J. {e}=-A_{rm} {fnK} {fnMicrosoft} {fnMicrosoft Sans Serif} {Barrier}/kT_{rm} {}}}
donde k es la constante de Boltzmann y la constante de proporcionalidad Ae es la constante de Richardson del emisor. En este caso, la dependencia de Je de Te se puede ajustar para producir We.
Función de trabajo del colector de electrones frío
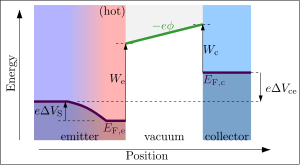
Se puede usar la misma configuración para medir la función de trabajo en el colector, simplemente ajustando el voltaje aplicado. Si se aplica un campo eléctrico lejos del emisor, entonces la mayoría de los electrones provenientes del emisor simplemente se reflejarán de regreso al emisor. Solo los electrones de mayor energía tendrán suficiente energía para llegar al colector, y la altura de la barrera potencial en este caso depende de la función de trabajo del colector, en lugar de la del emisor.
La actual todavía se rige por la ley de Richardson. Sin embargo, en este caso la altura de la barrera no depende de We. La altura de la barrera ahora depende de la función de trabajo del colector, así como de los voltajes adicionales aplicados:
- Ebarrier=Wc− − e()Δ Δ Vce− − Δ Δ VS){displaystyle E_{rm {}=W_{rm}-e(Delta V_{rm} {ce}- Delta V_{rm {S}}}
donde Wc es la función de trabajo termoiónico del colector, ΔVce es la tensión colector-emisor aplicada, y ΔVS es la tensión de Seebeck en el emisor caliente (la influencia de ΔVS a menudo se omite, ya que es una pequeña contribución del orden de 10 mV). La densidad de corriente resultante Jc a través del colector (por unidad de área del colector) está nuevamente dada por la Ley de Richardson, excepto que ahora
- Jc=ATe2e− − Ebarrier/kTe{displaystyle J. {c}=AT_{rm} {fnK} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn}} {fnMicrosoft}} {fnMicrosoft}}}} {f}}}}}}}}}}}}}}}}}¡E} {f} {f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnfnfnf}f}f}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn {Barrier}/kT_{rm} {}}}
donde A es una constante de tipo Richardson que depende del material del colector pero también puede depender del material del emisor y de la geometría del diodo. En este caso, la dependencia de Jc de Te, o de ΔVce, se puede ajustar para producir Wc.
Este método del potencial de retardo es uno de los métodos más simples y antiguos para medir funciones de trabajo, y es ventajoso ya que no se requiere que el material medido (colector) sobreviva a altas temperaturas.
Métodos basados en fotoemisión
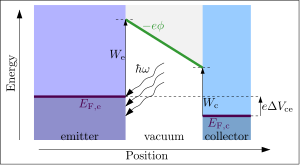
La función de trabajo fotoeléctrico es la energía mínima de fotones necesaria para liberar un electrón de una sustancia, en el efecto fotoeléctrico. Si la energía del fotón es mayor que la función de trabajo de la sustancia, la emisión fotoeléctrica ocurre y el electrón se libera de la superficie. Similar al caso termonico descrito anteriormente, los electrones liberados se pueden extraer en un coleccionista y producir una corriente detectable, si un campo eléctrico se aplica en la superficie del emisor. Exceso de energía foton resulta en un electrón liberado con energía cinética no cero. Se espera que la energía mínima de fotones ▪ ▪ ⋅ ⋅ {displaystyle hbar omega } requerido para liberar un electrón (y generar una corriente)
- ▪ ▪ ⋅ ⋅ =We{displaystyle hbar omega - ¿Qué?
donde We es la función de trabajo del emisor.
Las mediciones fotoeléctricas requieren mucho cuidado, ya que una geometría experimental diseñada incorrectamente puede resultar en una medición errónea de la función de trabajo. Esto puede ser responsable de la gran variación en los valores de la función de trabajo en la literatura científica. Además, la energía mínima puede ser engañosa en materiales donde no hay estados de electrones reales en el nivel de Fermi que estén disponibles para la excitación. Por ejemplo, en un semiconductor, la energía fotónica mínima en realidad correspondería al borde de la banda de valencia en lugar de a la función de trabajo.
Por supuesto, el efecto fotoeléctrico se puede usar en el modo de retardo, como con el aparato termoiónico descrito anteriormente. En el caso del retardo, se mide la función de trabajo del colector oscuro.
Método de la sonda Kelvin
La técnica de la sonda Kelvin se basa en la detección de un campo eléctrico (gradiente en ϕ) entre un material de muestra y el material de la sonda. El campo eléctrico puede variar según el voltaje ΔVsp que se aplica a la sonda en relación con la muestra. Si se elige el voltaje de manera que se elimine el campo eléctrico (la condición de vacío plano), entonces
- eΔ Δ Vsp=Ws− − Wp,cuandoφ φ es plana.{displaystyle eDelta V_{rm {}=W_{rm} {fnK}-W_{rm}quad {text{ when}~f} ~{text{is flat}}}
Dado que el experimentador controla y conoce ΔVsp, encontrar la condición de vacío plano da directamente la diferencia de la función de trabajo entre los dos materiales. La única pregunta es, ¿cómo detectar la condición de vacío plano? Normalmente, el campo eléctrico se detecta variando la distancia entre la muestra y la sonda. Cuando se cambia la distancia pero ΔVsp se mantiene constante, fluirá una corriente debido al cambio en la capacitancia. Esta corriente es proporcional al campo eléctrico del vacío, por lo que cuando el campo eléctrico se neutraliza, no fluirá corriente.
Aunque la técnica de la sonda Kelvin solo mide una diferencia de función de trabajo, es posible obtener una función de trabajo absoluta calibrando primero la sonda con un material de referencia (con una función de trabajo conocida) y luego usando la misma sonda para medir una muestra deseada. La técnica de la sonda Kelvin se puede utilizar para obtener mapas de funciones de trabajo de una superficie con una resolución espacial extremadamente alta, utilizando una punta afilada para la sonda (ver Microscopio de fuerza con sonda Kelvin).
Funciones de trabajo de los elementos
La función de trabajo depende de las configuraciones de los átomos en la superficie del material. Por ejemplo, en plata policristalina la función de trabajo es 4,26 eV, pero en cristales de plata varía para diferentes caras de cristal como (100) cara: 4,64 eV, (110) cara: 4,52 eV, (111) cara: 4,74 eV. Los rangos para las superficies típicas se muestran en la siguiente tabla.
| Ag | 4.26 – 4.74 | Al | 4.06 – 4.26 | As | 3.75 |
| Au | 5.10 – 5.47 | B | ~4.45 | Ba | 2.52 – 2.70 |
| Be | 4.98 | Bi | 4.31 | C | ~5 |
| Ca | 2.87 | Cd | 4.08 | Ce | 2.9 |
| Co | 5 | Cr | 4.5 | Cs | 1.95 |
| Cu | 4.53 – 5.10 | Eu | 2.5 | Fe: | 4.67 – 4.81 |
| Ga | 4.32 | Gd | 2.90 | Hf | 3.90 |
| Hg | 4.475 | In | 4.09 | Ir | 5.00 – 5.67 |
| K | 2.29 | La | 3.5 | Li | 2.9 |
| Lu | ~3.3 | Mg | 3.66 | Mn | 4.1 |
| Mo | 4.36 – 4.95 | Na | 2.36 | Nb | 3.95 – 4.87 |
| Nd | 3.2 | Ni | 5.04 – 5.35 | Os | 5.93 |
| Pb | 4.25 | Pd | 5.22 – 5.60 | Pt | 5.12 – 5.93 |
| Rb | 2.261 | Re | 4.72 | Rh | 4.98 |
| Ru | 4.71 | Sb | 4.55 – 4.70 | Sc | 3.5 |
| Se | 5.9 | Si | 4.60 – 4.85 | Sm | 2.7 |
| Sn | 4.42 | Sr | ~2.59 | Ta | 4.00 – 4.80 |
| Tb | 3.00 | Te | 4.95 | Th | 3.4 |
| Ti | 4.33 | Tl | ~3.84 | U | 3.63 – 3.90 |
| V | 4.3 | W | 4.32 – 4.55 | Y | 3.1 |
| Yb | 2.60 | Zn | 3.63 – 4.9 | Zr | 4.05 |
Factores físicos que determinan la función del trabajo
Debido a las complicaciones descritas en la siguiente sección de modelado, es difícil predecir teóricamente la función de trabajo con precisión. Sin embargo, se han identificado varias tendencias. La función de trabajo tiende a ser más pequeña para metales con una red abierta y más grande para metales en los que los átomos están muy juntos. Es algo más alto en las caras de cristal densas que en las caras de cristal abiertas, y también depende de las reconstrucciones de superficie para la cara de cristal dada.
Dipolo de superficie
La función de trabajo no depende simplemente del "nivel de vacío interno" dentro del material (es decir, su potencial electrostático promedio), debido a la formación de una doble capa eléctrica a escala atómica en la superficie. Este dipolo eléctrico superficial da un salto en el potencial electrostático entre el material y el vacío.
Una variedad de factores son responsables del dipolo eléctrico superficial. Incluso con una superficie completamente limpia, los electrones pueden dispersarse ligeramente en el vacío, dejando una capa de material ligeramente cargada positivamente. Esto ocurre principalmente en los metales, donde los electrones enlazados no encuentran un potencial de pared dura en la superficie, sino un potencial de aumento gradual debido a la atracción de la carga de la imagen. La cantidad de dipolo de superficie depende del diseño detallado de los átomos en la superficie del material, lo que lleva a la variación en la función de trabajo para las diferentes caras del cristal.
Dopaje y efecto de campo eléctrico (semiconductores)
En un semiconductor, la función de trabajo es sensible al nivel de dopaje en la superficie del semiconductor. Dado que el dopaje cerca de la superficie también puede controlarse mediante campos eléctricos, la función de trabajo de un semiconductor también es sensible al campo eléctrico en el vacío.
La razón de la dependencia es que, normalmente, el nivel de vacío y el borde de la banda de conducción conservan un espacio fijo independiente del dopaje. Este espacio se llama afinidad electrónica (tenga en cuenta que esto tiene un significado diferente al de la afinidad electrónica de la química); en el silicio, por ejemplo, la afinidad electrónica es de 4,05 eV. Si la afinidad electrónica EEA y el nivel de Fermi con referencia de banda de la superficie EF-EC son conocidos, entonces la función de trabajo viene dada por
- W=EEA+EC− − EF{displaystyle ¿Qué? {C}-E_{rm {F}}
donde EC se toma en la superficie.
De esto se podría esperar que al dopar la mayor parte del semiconductor, la función de trabajo se pueda ajustar. En realidad, sin embargo, las energías de las bandas cercanas a la superficie a menudo están ancladas al nivel de Fermi, debido a la influencia de los estados de la superficie. Si hay una gran densidad de estados superficiales, entonces la función de trabajo del semiconductor mostrará una dependencia muy débil del dopaje o del campo eléctrico.
Modelos teóricos de funciones metalúrgicas
El modelado teórico de la función de trabajo es difícil, ya que un modelo preciso requiere un tratamiento cuidadoso tanto de los efectos electrónicos como de la química superficial; ambos temas ya son complejos por derecho propio.
Uno de los primeros modelos exitosos para las tendencias de la función de trabajo del metal fue el modelo de gelatina, que permitió oscilaciones en la densidad electrónica cerca de la superficie abrupta (son similares a las oscilaciones de Friedel), así como la cola de la densidad de electrones que se extiende fuera de la superficie.. Este modelo mostró por qué la densidad de los electrones de conducción (representada por el radio de Wigner-Seitz rs) es un parámetro importante para determinar la función de trabajo.
El modelo de gelatina es solo una explicación parcial, ya que sus predicciones todavía muestran una desviación significativa de las funciones de trabajo reales. Los modelos más recientes se han centrado en incluir formas más precisas de intercambio de electrones y efectos de correlación, además de incluir la dependencia de la cara del cristal (esto requiere la inclusión de la red atómica real, algo que se descuida en el modelo de gelatina).
Dependencia de la temperatura de la función de trabajo de electrones
El comportamiento de electrones en metales varía con temperatura y se refleja en gran medida en la función de trabajo de electrones. Un modelo teórico para predecir la dependencia de temperatura de la función de trabajo de electrones, desarrollado por Rahemi et al. explica el mecanismo subyacente y predice esta dependencia de temperatura para varias estructuras de cristal mediante parámetros calculables y mensurables. En general, a medida que aumenta la temperatura, el EWF disminuye a través de φ φ ()T)=φ φ 0− − γ γ ()kBT)2φ φ 0{textstyle varphi (T)=varphi _{0}-gamma {frac {k_{text{B}T)^{2}}{varphi ♪♪ y γ γ {displaystyle gamma } es una propiedad material calculable que depende de la estructura de cristal (por ejemplo, BCC, FCC). φ φ 0{displaystyle varphi _{0} es la función de trabajo de electrones en T=0 y β β {displaystyle beta } es constante a lo largo del cambio.
Contenido relacionado
Efecto Joule-Thomson
Constante gravitacional
Marco de referencia inercial