Función de ventana

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Función utilizada en el procesamiento de señales

Una función de ventana popular, la ventana Hann. Las funciones de ventana más populares son curvas similares en forma de campana.

En procesamiento de señales y estadísticas, una función de ventana (también conocida como función de apodización o función de disminución) es una función matemática que se con valor cero fuera de algún intervalo elegido, normalmente simétrico alrededor de la mitad del intervalo, generalmente cerca de un máximo en el medio y generalmente disminuyendo desde el medio. Matemáticamente, cuando otra función o forma de onda/secuencia de datos se "multiplica" mediante una función de ventana, el producto también tiene valor cero fuera del intervalo: todo lo que queda es la parte donde se superponen, la "vista a través de la ventana". De manera equivalente, y en la práctica real, el segmento de datos dentro de la ventana se aísla primero y luego solo esos datos se multiplican por los valores de la función de ventana. Por lo tanto, la disminución, no la segmentación, es el objetivo principal de las funciones de ventana.

Las razones para examinar segmentos de una función más larga incluyen la detección de eventos transitorios y el promedio de tiempo de los espectros de frecuencia. La duración de los segmentos está determinada en cada aplicación por requisitos como resolución de tiempo y frecuencia. Pero ese método también cambia el contenido de frecuencia de la señal por un efecto llamado fuga espectral. Las funciones de ventana nos permiten distribuir la fuga espectralmente de diferentes maneras, según las necesidades de la aplicación en particular. Hay muchas opciones detalladas en este artículo, pero muchas de las diferencias son tan sutiles que resultan insignificantes en la práctica.

En aplicaciones típicas, las funciones de ventana utilizadas son no negativas, suaves, "en forma de campana" curvas. También se pueden usar rectángulos, triángulos y otras funciones. Una definición más general de funciones de ventana no requiere que sean idénticamente cero fuera de un intervalo, siempre que el producto de la ventana multiplicado por su argumento sea integrable al cuadrado y, más específicamente, que la función vaya lo suficientemente rápido hacia cero.

Aplicaciones

Las funciones de ventana se utilizan en el análisis, la modificación y la resíntesis espectrales, el diseño de filtros de respuesta de impulso finito, así como la formación de haces y el diseño de antenas.

Gráfico 2: La limpieza de un sinusoide causa fuga espectral. La misma cantidad de fuga ocurre si hay un número entero (azul) o no entero (rojo) de ciclos dentro de la ventana (huevos 1 y 2). Cuando el sinusoide se muestra y se venda, su discreto-time Fourier transforma también exhibe el mismo patrón de fuga (rows 3 y 4). Pero cuando el DTFT sólo se muestra escasamente, a un cierto intervalo, es posible (dependiendo de su punto de vista): (1) evitar la fuga, o (2) crear la ilusión de no fugarse. Para el caso del DTFT azul, esas muestras son las salidas de la discreta transformación Fourier (DFT). El DTFT rojo tiene el mismo intervalo de cero cruces, pero las muestras DFT caen entre ellos, y se revela la fuga.

Análisis espectral

La transformada de Fourier de la función $cos(ωt)$ es cero, excepto en la frecuencia ±ω. Sin embargo, muchas otras funciones y formas de onda no tienen transformadas de forma cerrada convenientes. Alternativamente, uno podría estar interesado en su contenido espectral solo durante un cierto período de tiempo.

En cualquier caso, la transformada de Fourier (o una transformada similar) se puede aplicar en uno o más intervalos finitos de la forma de onda. En general, la transformada se aplica al producto de la forma de onda y una función de ventana. Cualquier ventana (incluida la rectangular) afecta la estimación espectral calculada por este método.

Diseño de filtros

Las ventanas se utilizan a veces en el diseño de filtros digitales, en particular para convertir una imagen "ideal" respuesta de impulso de duración infinita, como una función sinc, a un diseño de filtro de respuesta de impulso finito (FIR). Eso se llama el método de la ventana.

Estadísticas y ajuste de curvas

Las funciones de ventana a veces se utilizan en el campo del análisis estadístico para restringir el conjunto de datos que se analizan a un rango cercano a un punto determinado, con un factor de ponderación que disminuye el efecto de los puntos más alejados de la parte de la curva que se ajusta.. En el campo del análisis bayesiano y el ajuste de curvas, esto se suele denominar núcleo.

Aplicaciones de ventana rectangular

Análisis de transitorios

Al analizar una señal transitoria en el análisis modal, como un impulso, una respuesta de choque, una ráfaga sinusoidal, una ráfaga de chirridos o una ráfaga de ruido, donde la distribución de energía frente al tiempo es extremadamente desigual, la ventana rectangular puede ser la más adecuada. Por ejemplo, cuando la mayor parte de la energía se encuentra al comienzo de la grabación, una ventana no rectangular atenúa la mayor parte de la energía, degradando la relación señal-ruido.

Análisis armónico

Uno podría desear medir el contenido armónico de una nota musical de un instrumento en particular o la distorsión armónica de un amplificador a una frecuencia determinada. Volviendo a la Figura 2, podemos observar que no hay fugas en un conjunto discreto de frecuencias armónicamente relacionadas muestreadas por la DFT. (Los nulos espectrales son en realidad cruces por cero, que no se pueden mostrar en una escala logarítmica como esta). Esta propiedad es exclusiva de la ventana rectangular y debe configurarse adecuadamente para la frecuencia de la señal, como se describe anteriormente.

Ventanas superpuestas

Cuando la longitud de un conjunto de datos que se va a transformar es mayor de lo necesario para proporcionar la resolución de frecuencia deseada, una práctica común es subdividirlo en conjuntos más pequeños y colocarlos en ventanas individualmente. Para mitigar la "pérdida" en los bordes de la ventana, los conjuntos individuales pueden superponerse en el tiempo. Consulte el método de análisis espectral de potencia de Welch y la transformada de coseno discreta modificada.

Ventanas bidimensionales

Las ventanas bidimensionales se utilizan comúnmente en el procesamiento de imágenes para reducir las frecuencias altas no deseadas en la imagen transforma Fourier. Se pueden construir a partir de ventanas de una dimensión en cualquiera de dos formas. La forma separable, ${displaystyle W(m,n)=w(m)w(n)}$ es trivial para calcular. La forma radial, ${displaystyle W(m,n)=w(r)}$ , que implica el radio $r={sqrt {(m-M/2)^{2}+(n-N/2)^{2}}}$ , es isotrópico, independiente en la orientación de los ejes de coordenadas. Sólo la función gaisiana es tanto separable como isotrópica. Las formas separables de todas las demás funciones de ventana tienen esquinas que dependen de la elección de los ejes de coordenadas. La isotropía/anisotropía de una función de ventana bidimensional es compartida por su transformación cuatridimensional. La diferencia entre las formas separables y radiales es similar al resultado de la difracción de las aberturas rectangulares vs. circulares, que se pueden visualizar en términos del producto de dos funciones sinc vs. una función Airy, respectivamente.

Una lista de funciones de ventana

Convenciones:

${displaystyle w_{0}(x)}$ es una función de fase cero (simétrica sobre $x=0$ ), continuo para ${displaystyle xin [-N/2,N/2],}$ Donde $N$ es un entero positivo (inteligente o extraño).
La secuencia ${displaystyle {w[n]=w_{0}(n-N/2),quad 0leq nleq N}}$ es simétrica, de longitud ${displaystyle N+1.}$
${displaystyle {w[n],quad 0leq nleq N-1}}$ es DFT-symmetric, de longitud ${displaystyle N.}$

El parámetro B mostrado en cada parcela espectral es el ruido equivalente de la función métrica de ancho de banda, en unidades de Cubos DFT.

El muestreo disperso de una DTFT (como las DFT de la figura 2) solo revela la fuga en los contenedores DFT desde una sinusoide cuya frecuencia también es un contenedor DFT entero. Los lóbulos laterales invisibles revelan la fuga que se espera de las sinusoides en otras frecuencias. Por lo tanto, al elegir una función de ventana, suele ser importante muestrear la DTFT más densamente (como lo hacemos a lo largo de esta sección) y elegir una ventana que suprima los lóbulos laterales a un nivel aceptable.

Ventana rectangular

La ventana rectangular (a veces conocida como furgón o ventana de Dirichlet) es la ventana más simple, equivalente a reemplazar todos menos N valores consecutivos de una secuencia de datos por ceros, lo que hace que parezca que la forma de onda se enciende y se apaga repentinamente:

{displaystyle w[n]=1.}

Otras ventanas están diseñadas para moderar estos cambios repentinos, lo que reduce la pérdida festoneada y mejora el rango dinámico, como se describe anteriormente (§ Análisis espectral).

La ventana rectangular es la ventana spline B de primer orden, así como la ventana de potencia de seno de potencia 0.

La ventana rectangular proporciona la estimación del error cuadrático medio mínimo de la transformada de Fourier de tiempo discreto, a costa de otros problemas discutidos.

Ventanas B-spline

Las ventanas

B-spline se pueden obtener como circunvoluciones de pliegue k de la ventana rectangular. Incluyen la ventana rectangular propiamente dicha (k = 1), la ventana § Triangular (k = 2) y la ventana § Parzen (k = 4). Las definiciones alternativas muestrean las funciones de base B-spline normalizadas apropiadas en lugar de las ventanas de tiempo discreto convolutivas. Una función base spline k^th-order B es una función polinomial por partes de grado k−1 que se obtiene mediante la autoconvolución de k veces de la función rectangular.

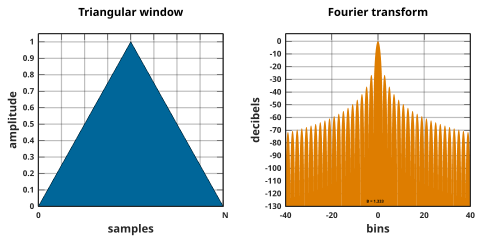
Ventana triangular

Ventana triangular (con L=N+ 1)

Las ventanas triangulares están dadas por:

{displaystyle w[n]=1-left|{frac {n-{frac {N}{2}}}{frac {L}{2}}}right|,quad 0leq nleq N}

donde L puede ser N, N + 1, o N + 2. La primera también se conoce como ventana Bartlett o ventana Fejér. Las tres definiciones convergen en general N.

La ventana triangular es la ventana spline B de segundo orden. La forma L = N puede verse como la convolución de dos ventanas rectangulares N/2 de ancho. La transformada de Fourier del resultado son los valores cuadrados de la transformada de la ventana rectangular de ancho medio.

Ventana de Parzen

Ventana de congelados

Definiendo $L ≜ N + 1$ , la ventana de Parzen, también conocida como de la Vallée Poussin window, es la ventana spline B de cuarto orden dada por:

<math alttext="{displaystyle w_{0}(n)triangleq left{{begin{array}{ll}1-6left({frac {n}{L/2}}right)^{2}left(1-{frac {|n|}{L/2}}right),&0leq |n|leq {frac {L}{4}}\2left(1-{frac {|n|}{L/2}}right)^{3}&{frac {L}{4}}w0()n)≜ ≜ {}1− − 6()nL/2)2()1− − SilencionSilencioL/2),0≤ ≤ SilencionSilencio≤ ≤ L42()1− − SilencionSilencioL/2)3L4.SilencionSilencio≤ ≤ L2}{displaystyle w_{0}(n)triangleq left{begin{array}{ll}1-6left({frac {n}{L/2}right)}left(1-{frac] {fnse}{L/2}}right), tarde0leq {L}{4}2left(1-{frac} {fnh} {fnh} {fnh}} {fnh} {fnh}} {fn}}fn}fn}fn}fn}fn}fn}fn}fn}f}fn}f}fnfnfnfn}}fnfnfnfnfn}}}fn}}fnfnfnfnfnfnfnfnfnfnfnfnfn}}}fnfnfnfnfn}}}}fn}}}}}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}}}}fnh}}}}}}}<img alt="{displaystyle w_{0}(n)triangleq left{{begin{array}{ll}1-6left({frac {n}{L/2}}right)^{2}left(1-{frac {|n|}{L/2}}right),&0leq |n|leq {frac {L}{4}}\2left(1-{frac {|n|}{L/2}}right)^{3}&{frac {L}{4}}

{displaystyle w[n]= w_{0}left(n-{tfrac {N}{2}}right), 0leq nleq N}

Ventana Welch

Otras ventanas polinómicas

Ventana de Welch

La ventana de Welch consta de una sola sección parabólica:

{displaystyle w[n]=1-left({frac {n-{frac {N}{2}}}{frac {N}{2}}}right)^{2},quad 0leq nleq N.}

El polinomio cuadrático definidor alcanza un valor de cero en las muestras justo fuera del intervalo de la ventana.

Ventana de seno

Ventana de Sine

{displaystyle w[n]=sin left({frac {pi n}{N}}right)=cos left({frac {pi n}{N}}-{frac {pi }{2}}right),quad 0leq nleq N.}

El correspondiente $w_{0}(n),$ función es un cosine sin $π$ /2 fase offset. Así que... sine ventana a veces también se llama ventana cosine. Como representa medio ciclo de una función sinusoidal, también se conoce variamente como ventana mediana o ventanilla media-cosina.

La autocorrelación de una ventana sinusoidal produce una función conocida como ventana de Bowman.

Ventanas de potencia de seno/coseno

Estas funciones de ventana tienen la forma:

{displaystyle w[n]=sin ^{alpha }left({frac {pi n}{N}}right)=cos ^{alpha }left({frac {pi n}{N}}-{frac {pi }{2}}right),quad 0leq nleq N.}

La ventana rectangular ( $α = 0$ ), la ventana de seno ( $α = 1$ ), y la ventana de Hann ( $α = 2$ ) son miembros de esta familia.

Para valores enteros pares de $α$ , estas funciones también se pueden expresar en forma de suma de coseno:

{displaystyle w[n]=a_{0}-a_{1}cos left({frac {2pi n}{N}}right)+a_{2}cos left({frac {4pi n}{N}}right)-a_{3}cos left({frac {6pi n}{N}}right)+a_{4}cos left({frac {8pi n}{N}}right)-...}

{displaystyle {begin{array}{l|llll}hline alpha &a_{0}&a_{1}&a_{2}&a_{3}&a_{4}\hline 0&1\2&0.5&0.5\4&0.375&0.5&0.125\6&0.3125&0.46875&0.1875&0.03125\8&0.2734375&0.4375&0.21875&0.0625&7.8125times 10^{-3}\hline end{array}}}

Ventanas de suma de coseno

Esta familia también se conoce como ventanas de coseno generalizadas.

{displaystyle w[n]=sum _{k=0}^{K}(-1)^{k}a_{k};cos left({frac {2pi kn}{N}}right),quad 0leq nleq N.}

()Eq.1)

En la mayoría de los casos, incluidos los ejemplos a continuación, todos los coeficientes a_k ≥ 0. Estas ventanas tienen solo 2K + 1 coeficientes DFT de N puntos distintos de cero.

Ventanas de Hann y Hamming

Hann ventana

Ventilador, a₀= 0,53836 y a₁= 0.46164. La ventana original de Hamming habría a₀= 0,54 y a₁= 0,46.

Las ventanas habituales de suma de cosenos para el caso K = 1 tienen la forma:

{displaystyle w[n]=a_{0}-underbrace {(1-a_{0})} _{a_{1}}cdot cos left({tfrac {2pi n}{N}}right),quad 0leq nleq N,}

que se confunde fácilmente (ya menudo) con su versión de fase cero:

{displaystyle {begin{aligned}w_{0}(n) &=wleft[n+{tfrac {N}{2}}right]\&=a_{0}+a_{1}cdot cos left({tfrac {2pi n}{N}}right),quad -{tfrac {N}{2}}leq nleq {tfrac {N}{2}}.end{aligned}}}

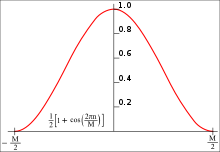
Ajuste ${displaystyle a_{0}=0.5}$ produce a ventana Hann:

{displaystyle w[n]=0.5;left[1-cos left({frac {2pi n}{N}}right)right]=sin ^{2}left({frac {pi n}{N}}right),}

nombrado por Julius von Hann, y a veces erróneamente referido como Hanning, presumiblemente debido a sus similitudes lingüísticas y fórmulas con la ventana Hamming. También se conoce como Cosine, porque la versión de cero fase, ${displaystyle w_{0}(n),}$ es un lóbulo de una función cosina elevada.

Esta función es miembro de las familias de suma de coseno y potencia del seno. A diferencia de la ventana de Hamming, los puntos finales de la ventana de Hann simplemente tocan cero. Los lóbulos laterales resultantes caen a unos 18 dB por octava.

Ajuste $a_{0}$ a aproximadamente 0,54, o más precisamente 25/46, produce los Ventilador, propuesto por Richard W. Hamming. Esa elección coloca un cero cruce a la frecuencia 5 $π$ /(N− 1), que cancela el primer sidelobe de la ventana de Hann, dándole una altura de aproximadamente una quinta parte la de la ventana de Hann. La ventana de Hamming se llama a menudo Hamming blip cuando se usa para dar forma al pulso.

La aproximación de los coeficientes a dos decimales reduce sustancialmente el nivel de los lóbulos laterales, a una condición de casi equiondulación. En el sentido de equionda, los valores óptimos para los coeficientes son a₀ = 0,53836 y a₁ = 0,46164.

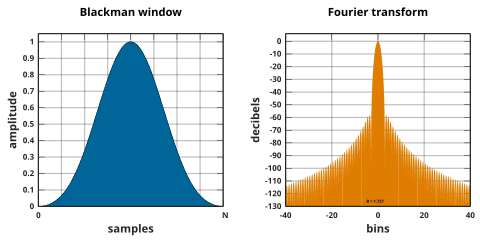
Ventana Blackman

Ventana Blackman;

α = 0,16

Las ventanas de Blackman se definen como:

{displaystyle w[n]=a_{0}-a_{1}cos left({frac {2pi n}{N}}right)+a_{2}cos left({frac {4pi n}{N}}right)}

{displaystyle a_{0}={frac {1-alpha }{2}};quad a_{1}={frac {1}{2}};quad a_{2}={frac {alpha }{2}}.}

Por convención común, el término no calificado ventana de Blackman se refiere a la "propuesta no muy seria" de Blackman; de $α = 0,16$ (a₀ = 0,42, a₁ = 0,5, a₂ = 0,08), que se aproxima mucho al Blackman exacto, con a₀ = 7938/18608 ≈ 0,42659, a₁ = 9240/18608 ≈ 0,49656 y a₂ = 1430/18608 ≈ 0,076849. Estos valores exactos colocan ceros en el tercer y cuarto lóbulo lateral, pero dan como resultado una discontinuidad en los bordes y una caída de 6 dB/oct. Los coeficientes truncados no anulan los lóbulos laterales también, pero tienen una disminución mejorada de 18 dB/oct.

Ventana Nuttall, primera derivada continua

Ventana Nuttall, primera derivación continua

La forma continua de la ventana Nuttall, ${displaystyle w_{0}(x),}$ y su primer derivado son continuos en todas partes, como la función Hann. Es decir, la función va a 0 a x= ±N/2, a diferencia de las ventanas Blackman-Nuttall, Blackman-Harris y Hamming. La ventana de Blackman $α = 0,16$ ) es también continuo con derivación continua en el borde, pero la "exacta ventana Blackman" no es.

{displaystyle w[n]=a_{0}-a_{1}cos left({frac {2pi n}{N}}right)+a_{2}cos left({frac {4pi n}{N}}right)-a_{3}cos left({frac {6pi n}{N}}right)}

{displaystyle a_{0}=0.355768;quad a_{1}=0.487396;quad a_{2}=0.144232;quad a_{3}=0.012604.}

Ventana Blackman-Nuttall

Blackman-Nuttall ventana

{displaystyle w[n]=a_{0}-a_{1}cos left({frac {2pi n}{N}}right)+a_{2}cos left({frac {4pi n}{N}}right)-a_{3}cos left({frac {6pi n}{N}}right)}

{displaystyle a_{0}=0.3635819;quad a_{1}=0.4891775;quad a_{2}=0.1365995;quad a_{3}=0.0106411.}

Ventana Blackman-Harris

Blackman-Harris ventana

Una generalización de la familia Hamming, producida al agregar más funciones sinc desplazadas, destinadas a minimizar los niveles de lóbulo lateral

{displaystyle w[n]=a_{0}-a_{1}cos left({frac {2pi n}{N}}right)+a_{2}cos left({frac {4pi n}{N}}right)-a_{3}cos left({frac {6pi n}{N}}right)}

{displaystyle a_{0}=0.35875;quad a_{1}=0.48829;quad a_{2}=0.14128;quad a_{3}=0.01168.}

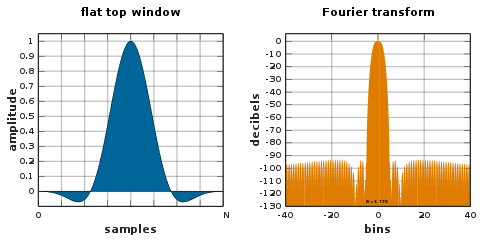
Ventana superior plana

Ventana plana

Una ventana de parte superior plana es una ventana de valor parcialmente negativo que tiene una pérdida mínima de ondulación en el dominio de la frecuencia. Esa propiedad es deseable para la medición de amplitudes de componentes de frecuencia sinusoidal. Sin embargo, su amplio ancho de banda da como resultado un alto ancho de banda de ruido y una selección de frecuencia más amplia, lo que, dependiendo de la aplicación, podría ser un inconveniente.

Las ventanas superiores planas se pueden diseñar utilizando métodos de diseño de filtro de paso bajo, o pueden ser de la variedad habitual de suma de coseno:

{displaystyle {begin{aligned}w[n]=a_{0}&{}-a_{1}cos left({frac {2pi n}{N}}right)+a_{2}cos left({frac {4pi n}{N}}right)\&{}-a_{3}cos left({frac {6pi n}{N}}right)+a_{4}cos left({frac {8pi n}{N}}right).end{aligned}}}

La variante de Matlab tiene estos coeficientes:

{displaystyle a_{0}=0.21557895;quad a_{1}=0.41663158;quad a_{2}=0.277263158;quad a_{3}=0.083578947;quad a_{4}=0.006947368.}

Hay otras variaciones disponibles, como lóbulos laterales que se deslizan a costa de valores más altos cerca del lóbulo principal.

Ventanas Rife-Vincent

Las ventanas de Rife-Vincent se escalan habitualmente para el valor promedio de la unidad, en lugar del valor máximo de la unidad. Los valores de los coeficientes a continuación, aplicados a la Eq.1, reflejan esa costumbre.

Clase I, Orden 1K = 1): ${displaystyle a_{0}=1;quad a_{1}=1}$ Funcionalmente equivalente a la ventana Hann.

Clase I, Orden 2K = 2): ${displaystyle a_{0}=1;quad a_{1}={tfrac {4}{3}};quad a_{2}={tfrac {1}{3}}}$

La clase I se define minimizando la amplitud del lóbulo lateral de alto orden. Se tabulan los coeficientes para órdenes hasta K=4.

La clase II minimiza el ancho del lóbulo principal para un lóbulo lateral máximo dado.

La Clase III es un compromiso para el cual el orden K = 2 se asemeja a la ventana § Blackman.

Ventanas ajustables

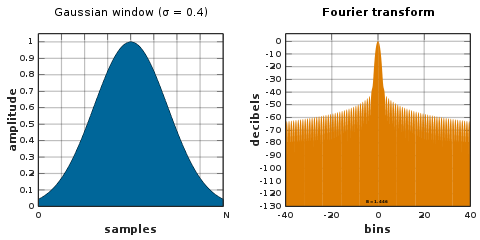
Ventana gaussiana

Ventana Gaussiana, σ= 0,4

La transformada de Fourier de una gaussiana también es una gaussiana. Dado que el soporte de una función gaussiana se extiende hasta el infinito, debe truncarse en los extremos de la ventana o debe dividirse en otra ventana que termine en cero.

Dado que el logaritmo de un gaussiano produce una parábola, esto se puede usar para una interpolación cuadrática casi exacta en la estimación de frecuencia.

{displaystyle w[n]=exp left(-{frac {1}{2}}left({frac {n-N/2}{sigma N/2}}right)^{2}right),quad 0leq nleq N.}

sigma leq ;0.5,

La desviación estándar de la función gaussiana es σ · N/2 períodos de muestreo.

Ventana Gaussiana confiada, σ_t= 0,1

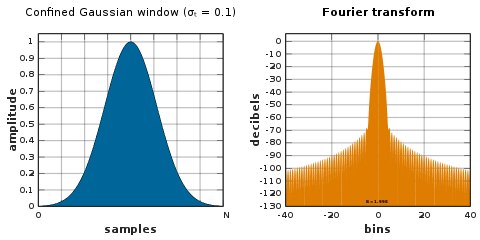
Ventana gaussiana confinada

La ventana gaussiana confinada produce el ancho de frecuencia cuadrático medio más pequeño posible $σ ω$ para un ancho temporal dado $(N + 1) σ t . Estas ventanas optimizan los productos de ancho de banda de tiempo-frecuencia RMS. Se calculan como los vectores propios mínimos de una matriz dependiente de parámetros. La familia de ventanas gaussianas confinadas contiene la ventana § Seno y la ventana § Gaussiana en los casos límite de grandes y pequeños σ t, respectivamente.$

Confinación aproximada Ventana Gaussiana,

σ t = 0,1

Ventana gaussiana confinada aproximada

Definiendo $L ≜ N + 1$ , una ventana gaussiana confinada de ancho temporal $L \times σ t$ se aproxima bien mediante:

{displaystyle w[n]=G(n)-{frac {G(-{tfrac {1}{2}})[G(n+L)+G(n-L)]}{G(-{tfrac {1}{2}}+L)+G(-{tfrac {1}{2}}-L)}}}

Donde $G$ es una función Gausiana:

{displaystyle G(x)=exp left(-left({cfrac {x-{frac {N}{2}}}{2Lsigma _{t}}}right)^{2}right)}

La desviación estándar de la ventana aproximada es asintóticamente igual (es decir, valores grandes de $N$ ) a $L \times σ t$ para $σ t < 0,14$ .

Ventana normal generalizada

Una versión más generalizada de la ventana gaussiana es la ventana normal generalizada. Conservando la notación de la ventana gaussiana anterior, podemos representar esta ventana como

{displaystyle w[n,p]=exp left(-left({frac {n-N/2}{sigma N/2}}right)^{p}right)}

para cualquier $p$ . At $p=2$ , esta es una ventana de Gauss $p$ enfoques $infty$ , esto se aproxima a una ventana rectangular. La transformación Fourier de esta ventana no existe en forma cerrada para un general $p$ . Sin embargo, demuestra los otros beneficios de ser suave, ajustable ancho de banda. Al igual que la ventana § Tukey, esta ventana ofrece naturalmente una "superior plana" para controlar la atenuación de la amplitud de una serie de tiempo (sobre la cual no tenemos un control con la ventana Gausian). En esencia, ofrece un buen compromiso (controlable), en términos de fuga espectral, resolución de frecuencia y atenuación de amplitud, entre la ventana Gausiana y la ventana rectangular. Vea también para un estudio sobre la representación de la frecuencia de tiempo de esta ventana (o función).

Ventana Tukey

Ventana de pavo,

α = 0,5

La ventana de Tukey, también conocida como ventana cónica del coseno, se puede considerar como un lóbulo coseno de ancho $Nα /2$ (que abarca $Nα /2 + 1$ observaciones) que se convoluciona con una ventana rectangular de ancho $N (1 - α /2)$ .

<math alttext="{displaystyle left.{begin{array}{lll}w[n]={frac {1}{2}}left[1-cos left({frac {2pi n}{alpha N}}right)right],quad &{frac {alpha N}{2}}leq nleq {frac {N}{2}}\w[n]=1,quad &0leq nw[n]=12[1− − #⁡ ⁡ ()2π π nα α N)],α α N2≤ ≤ n≤ ≤ N2w[n]=1,0≤ ≤ n.α α N2w[N− − n]=w[n],0≤ ≤ n≤ ≤ N2}{displaystyle left.{begin{lll}w[n]={frac {1}{2}}left[1-cos left({frac {2pi n}{alpha N}right)right],quad >{frac {frac}{fn] {fn} {fn}fnh}fnh}fnhn}=1,quad No. {fnMicrosoft} ¿Qué?<img alt="{displaystyle left.{begin{array}{lll}w[n]={frac {1}{2}}left[1-cos left({frac {2pi n}{alpha N}}right)right],quad &{frac {alpha N}{2}}leq nleq {frac {N}{2}}\w[n]=1,quad &0leq n

En $α = 0$ se vuelve rectangular, y en $α = 1$ se convierte en una ventana de Hann.

Ventana con cono de Planck

Ventana de pañales, ε= 0,1

La llamada ventana "Planck-taper" es una función de parachoques que ha sido ampliamente utilizada en la teoría de particiones de unidad en múltiples ejes. Es suave (a $C^{infty }$ función) en todas partes, pero es exactamente cero fuera de una región compacta, exactamente uno sobre un intervalo dentro de esa región, y varía suave y monotonicamente entre esos límites. Su uso como función de ventana en el procesamiento de señales se sugirió primero en el contexto de la astronomía de onda gravitacional, inspirada en la distribución Planck. Se define como una función manual:

<math alttext="{displaystyle left.{begin{array}{lll}w[0]=0,\w[n]=left(1+exp left({frac {varepsilon N}{n}}-{frac {varepsilon N}{varepsilon N-n}}right)right)^{-1},quad &1leq nw[0]=0,w[n]=()1+exp⁡ ⁡ ()ε ε Nn− − ε ε Nε ε N− − n))− − 1,1≤ ≤ n.ε ε Nw[n]=1,ε ε N≤ ≤ n≤ ≤ N2w[N− − n]=w[n],0≤ ≤ n≤ ≤ N2}{displaystyle left.{begin{lll}w[0]=0,w[n]=left(1+exp left({frac {varepsilon No. ################################################################################################################################################################################################################################################################ Nw[n]=1,quad > Nleq nleq {fn}w[N-n]=w[n],quad &0leq nleq {frac {fn}end{array}right}<img alt="{displaystyle left.{begin{array}{lll}w[0]=0,\w[n]=left(1+exp left({frac {varepsilon N}{n}}-{frac {varepsilon N}{varepsilon N-n}}right)right)^{-1},quad &1leq n

La cantidad de disminución es controlada por el parámetro ε, con valores más pequeños dando transiciones más nítidas.

Ventana DPSS o Slepian

El DPSS (secuencia esferoidal alargada discreta) o la ventana Slepian maximiza la concentración de energía en el lóbulo principal y se utiliza en el análisis espectral multitaper, que promedia el ruido en el espectro y reduce la pérdida de información en los bordes de la ventana.

El lóbulo principal termina en un rango de frecuencia dado por el parámetro α.

ventana DPSS, α= 2

ventana DPSS, α= 3

Las siguientes ventanas Kaiser se crean mediante una simple aproximación a las ventanas DPSS:

Kaiser ventana, α= 2

Kaiser ventana, α= 3

Ventana Kaiser

La ventana Kaiser, o Kaiser-Bessel, es una aproximación simple de la ventana DPSS que usa funciones de Bessel, descubierta por James Kaiser.

{displaystyle w[n]={frac {I_{0}left(pi alpha {sqrt {1-left({frac {2n}{N}}-1right)^{2}}}right)}{I_{0}(pi alpha)}},quad 0leq nleq N}

{displaystyle w_{0}(n)={frac {I_{0}left(pi alpha {sqrt {1-left({frac {2n}{N}}right)^{2}}}right)}{I_{0}(pi alpha)}},quad -N/2leq nleq N/2}

Donde $I_{0}$ es la función de Bessel modificada del primer tipo. Parámetro variable $alpha$ determina el intercambio entre el ancho principal del lóbulo y los niveles laterales del patrón de fuga espectral. El ancho principal del lóbulo, entre las nulas, es dado por $2{sqrt {1+alpha ^{2}}},$ en unidades de contenedores DFT, y un valor típico $alpha$ 3.

Ventana Dolph-Chebyshev

Ventana Dolph-Chebyshev, α= 5

Minimiza la norma de Chebyshev de los lóbulos laterales para un ancho de lóbulo principal determinado.

La función de la ventana Dolph-Chebyshev de fase cero ${displaystyle w_{0}[n]}$ se define generalmente en términos de su discreto de valor real Fourier transform, ${displaystyle W_{0}[k]}$ :

{displaystyle W_{0}(k)={frac {T_{N}{big (}beta cos left({frac {pi k}{N+1}}right){big)}}{T_{N}(beta)}}={frac {T_{N}{big (}beta cos left({frac {pi k}{N+1}}right){big)}}{10^{alpha }}}, 0leq kleq N.}

T_n(x) es el n-ésimo polinomio de Chebyshev del primer tipo evaluado en x, que se puede calcular usando

{displaystyle T_{n}(x)={begin{cases}cos !{big (}ncos ^{-1}(x){big)}&{text{if }}-1leq xleq 1\cosh !{big (}ncosh ^{-1}(x){big)}&{text{if }}xgeq 1\(-1)^{n}cosh !{big (}ncosh ^{-1}(-x){big)}&{text{if }}xleq -1,end{cases}}}

{displaystyle beta =cosh !{big (}{tfrac {1}{N}}cosh ^{-1}(10^{alpha }){big)}}

es la única solución positiva real ${displaystyle T_{N}(beta)=10^{alpha }}$ , donde el parámetro α establece la norma Chebyshev de los sidelobes a −20αdecibeles.

La función de ventana se puede calcular a partir de W₀(k) mediante una transformada de Fourier discreta inversa (DFT):

{displaystyle w_{0}(n)={frac {1}{N+1}}sum _{k=0}^{N}W_{0}(k)cdot e^{i2pi kn/(N+1)}, -N/2leq nleq N/2.}

La versión retrasada de la ventana se puede obtener mediante:

{displaystyle w[n]=w_{0}left(n-{frac {N}{2}}right),quad 0leq nleq N,}

que para valores pares de N debe calcularse de la siguiente manera:

{displaystyle {begin{aligned}w_{0}left(n-{frac {N}{2}}right)={frac {1}{N+1}}sum _{k=0}^{N}W_{0}(k)cdot e^{frac {i2pi k(n-N/2)}{N+1}}={frac {1}{N+1}}sum _{k=0}^{N}left[left(-e^{frac {ipi }{N+1}}right)^{k}cdot W_{0}(k)right]e^{frac {i2pi kn}{N+1}},end{aligned}}}

que es un DFT inverso ${displaystyle left(-e^{frac {ipi }{N+1}}right)^{k}cdot W_{0}(k).}$

Variaciones:

Debido a la condición equiripple, la ventana de tiempo-dominio tiene discontinuidades en los bordes. Una aproximación que los evita, permitiendo que los equiripples caigan en los bordes, es una ventana de Taylor.
También está disponible una alternativa a la definición DFT inversa. [1].

Ventana ultraesférica

La ventana Ultraesférica μ El parámetro determina si las amplitudes laterales de Fourier transforman disminuyen, son de nivel o aumentan con frecuencia.

La ventana ultraesférica fue presentada en 1984 por Roy Streit y tiene aplicación en el diseño de conjuntos de antenas, el diseño de filtros no recursivos y el análisis de espectro.

Al igual que otras ventanas ajustables, la ventana ultraesférica tiene parámetros que se pueden usar para controlar el ancho del lóbulo principal de la transformada de Fourier y la amplitud relativa del lóbulo lateral. A diferencia de otras ventanas, tiene un parámetro adicional que se puede usar para establecer la velocidad a la que los lóbulos laterales disminuyen (o aumentan) en amplitud.

La ventana se puede expresar en el dominio del tiempo de la siguiente manera:

{displaystyle w[n]={frac {1}{N+1}}left[C_{N}^{mu }(x_{0})+sum _{k=1}^{frac {N}{2}}C_{N}^{mu }left(x_{0}cos {frac {kpi }{N+1}}right)cos {frac {2npi k}{N+1}}right]}

Donde $C_{N}^{mu }$ es el polinomio Ultraesférico del grado N, y $x_{0}$ y $mu$ controla los patrones de lobo lateral.

Ciertos valores específicos $mu$ rendimiento de otras ventanas bien conocidas: $mu =0$ y $mu =1$ dar las ventanas Dolph-Chebyshev y Saramäki respectivamente. Vea aquí para ilustrar las ventanas ultraesféricas con variada parametrización.

Ventana exponencial o de Poisson

Ventana exponencial, τ=N/2

Ventana exponencial, τ=N/2)/(60/8.69)

La ventana de Poisson, o más genéricamente, la ventana exponencial aumenta exponencialmente hacia el centro de la ventana y disminuye exponencialmente en la segunda mitad. Dado que la función exponencial nunca llega a cero, los valores de la ventana en sus límites son distintos de cero (puede verse como la multiplicación de una función exponencial por una ventana rectangular). se define por

{displaystyle w[n]=e^{-left|n-{frac {N}{2}}right|{frac {1}{tau }}},}

donde τ es la constante de tiempo de la función. La función exponencial decae como e ≃ 2,71828 o aproximadamente 8,69 dB por constante de tiempo. Esto significa que para un decaimiento específico de D dB en la mitad de la longitud de la ventana, la constante de tiempo τ viene dada por

tau ={frac {N}{2}}{frac {8.69}{D}}.

Ventanas híbridas

Las funciones de ventana también se han construido como combinaciones multiplicativas o aditivas de otras ventanas.

Bartlett-Hann ventana

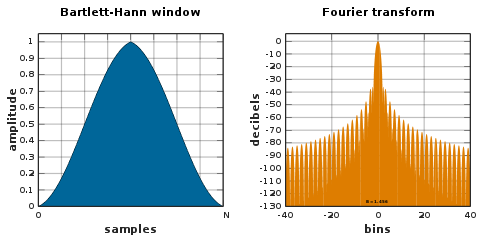
Ventana Bartlett-Hann

{displaystyle w[n]=a_{0}-a_{1}left|{frac {n}{N}}-{frac {1}{2}}right|-a_{2}cos left({frac {2pi n}{N}}right)}

a_{0}=0.62;quad a_{1}=0.48;quad a_{2}=0.38,

Ventana de Planck-Bessel

Planck-Bessel ventana, ε= 0.1, α= 4.45

Una ventana de cono de Planck multiplicada por una ventana de Kaiser que se define en términos de una función de Bessel modificada. Esta función de ventana híbrida se introdujo para disminuir el nivel máximo del lóbulo lateral de la ventana cónica de Planck mientras se sigue explotando su buen decaimiento asintótico. Tiene dos parámetros sintonizables, ε del cono de Planck y α de la ventana Kaiser, por lo que puede ajustarse para adaptarse a los requisitos de una señal dada.

Ventana de Hann-Poisson

Hann-Poisson ventana, α= 2

Una ventana de Hann multiplicada por una ventana de Poisson. Para ${displaystyle alpha geqslant 2}$ no tiene lóbulos laterales, como sus Fourier transforma cae para siempre lejos del lóbulo principal sin minima local. Así se puede utilizar en algoritmos de escalada de colinas como el método de Newton. La ventana Hann-Poisson se define por:

{displaystyle w[n]={frac {1}{2}}left(1-cos left({frac {2pi n}{N}}right)right)e^{frac {-alpha left|N-2nright|}{N}},}

donde α es un parámetro que controla la pendiente de la exponencial.

Otras ventanas

Ventana GAP (ventana Nuttall optimizada GAP)

Ventana de polinomio adaptativo generalizado (GAP)

La ventana GAP es una familia de funciones de ventana ajustables que se basan en una expansión polinómica simétrica del orden $K$ . Es continuo con derivación continua en todas partes. Con el conjunto adecuado de coeficientes de expansión y orden de expansión, la ventana GAP puede imitar todas las funciones de ventana conocidas, reproduciendo con precisión sus propiedades espectrales.

{displaystyle w_{0}[n]=a_{0}+sum _{k=1}^{K}a_{2k}left({frac {n}{sigma }}right)^{2k},quad -{frac {N}{2}}leq nleq {frac {N}{2}},}

Donde $sigma$ es la desviación estándar de la ${n}$ secuencia.

Además, comenzando con un conjunto de coeficientes de expansión $a_{{2k}}$ que imita una función de ventana conocida, la ventana GAP se puede optimizar mediante procedimientos de minimización para conseguir un nuevo conjunto de coeficientes que mejoran una o más propiedades espectrales, como el ancho principal del lóbulo, atenuación del lóbulo lateral y la tasa de caída del lóbulo lateral. Por lo tanto, una función de ventana GAP se puede desarrollar con propiedades espectrales diseñadas dependiendo de la aplicación específica.

Ventana de Sinc o Lanczos

Ventana de Lanczos

{displaystyle w[n]=operatorname {sinc} left({frac {2n}{N}}-1right)}

usados en resonancia Lanczos
para la ventana de Lanczos, ${displaystyle operatorname {sinc} (x)}$ se define como ${displaystyle sin(pi x)/pi x}$
también conocido como Sinc ventana, porque: ${displaystyle w_{0}(n)=operatorname {sinc} left({frac {2n}{N}}right),}$ es el lóbulo principal de una función sinc normalizada

Funciones de ventana asimétrica

El ${displaystyle w_{0}(x)}$ forma, definida arriba, es simétrica alrededor $x=0$ . Sin embargo, hay funciones de ventana que son asimétricas como la distribución Gamma utilizada en la implementación de FIR de filtros Gammatone. Estas asimetrías se utilizan para reducir el retraso al usar grandes tamaños de ventana o para enfatizar el transito inicial de un pulso de descaying. Hay maneras de hacer normalmente las ventanas simétricas asimétricas como esta abajo aplicando esta fórmula:

{displaystyle x=x^{alpha }}

a la función del tiempo (x la posición se cambia así que es 0 a 1 para aplicar esta fórmula arriba antes de mapearla de nuevo a -1 a 1 rango), donde la ventana se desplaza hacia las últimas muestras donde $1}" xmlns="http://www.w3.org/1998/Math/MathML">α α ■1{displaystyle alpha }1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/17d81dbbc4786493c7b8548cc324a978d7cf5dbd" style="vertical-align: -0.338ex; width:5.749ex; height:2.176ex;"/>$ y a la inversa a las primeras muestras cuando $<math alttext="{displaystyle alpha α α .1{displaystyle alpha. <img alt="alpha$ .

Citas de página

^ Harris 1978, p 57, fig 10.

Contenido relacionado

Más resultados...