Función de onda

Comparación de las concepciones de oscilador armónico clásico y cuántico para una sola partícula sin espinas. Los dos procesos difieren mucho. El proceso clásico (A–B) está representado como el movimiento de una partícula a lo largo de una trayectoria. El proceso cuántico (C-H) no tiene tal trayectoria. Más bien, se representa como una ola; aquí, el eje vertical muestra la parte real (azul) e parte imaginaria (rojo) de la función de onda. Los paneles (C-F) muestran cuatro soluciones de onda fija diferentes de la ecuación Schrödinger. Los paneles (G-H) muestran además dos funciones de onda diferentes que son soluciones de la ecuación Schrödinger pero no ondas de pie.

En física cuántica, una función de onda es una descripción matemática del estado cuántico de un sistema cuántico aislado. La función de onda es una amplitud de probabilidad de valor complejo, y de ella se pueden derivar las probabilidades de los posibles resultados de las mediciones realizadas en el sistema. Los símbolos más comunes para una función de onda son las letras griegas ψ y Ψ (minúsculas y capital psi, respectivamente).

La función de onda es una función de los grados de libertad correspondientes a un conjunto máximo de observables conmutables. Una vez que se elige tal representación, la función de onda se puede derivar del estado cuántico.

Para un sistema dado, la elección de qué grados de libertad de conmutación usar no es única y, en consecuencia, el dominio de la función de onda tampoco es único. Por ejemplo, puede tomarse como una función de todas las coordenadas de posición de las partículas sobre el espacio de posiciones, o los momentos de todas las partículas sobre el espacio de momentos; los dos están relacionados por una transformada de Fourier. Algunas partículas, como los electrones y los fotones, tienen un espín distinto de cero, y la función de onda de dichas partículas incluye el espín como un grado de libertad discreto e intrínseco; también se pueden incluir otras variables discretas, como isospin. Cuando un sistema tiene grados de libertad internos, la función de onda en cada punto de los grados de libertad continuos (por ejemplo, un punto en el espacio) asigna un número complejo para cada valor posible de los grados de libertad discretos (p. ej., componente z del espín): estos valores a menudo se muestran en una matriz de columna (p. ej., un vector de columna 2 × 1 para un electrón no relativista con espín 1⁄2 ).

Según el principio de superposición de la mecánica cuántica, las funciones de onda se pueden sumar y multiplicar por números complejos para formar nuevas funciones de onda y formar un espacio de Hilbert. El producto interno entre dos funciones de onda es una medida de la superposición entre los estados físicos correspondientes y se utiliza en la interpretación probabilística fundamental de la mecánica cuántica, la regla de Born, que relaciona las probabilidades de transición con los productos internos. La ecuación de Schrödinger determina cómo evolucionan las funciones de onda con el tiempo, y una función de onda se comporta cualitativamente como otras ondas, como las ondas de agua o las ondas en una cuerda, porque la ecuación de Schrödinger es matemáticamente un tipo de ecuación de onda. Esto explica el nombre de "función de onda" y da lugar a la dualidad onda-partícula. Sin embargo, la función de onda en la mecánica cuántica describe un tipo de fenómeno físico, aún abierto a diferentes interpretaciones, que difiere fundamentalmente del de las ondas mecánicas clásicas.

En la interpretación estadística de Born en la mecánica cuántica no relativista, el módulo cuadrado de la función de onda, |ψ|², es un número real interpretado como la densidad de probabilidad de medir una partícula como si estuviera en un lugar dado, o teniendo un momento dado, en un momento dado, y posiblemente tener valores definidos para grados de libertad discretos. La integral de esta cantidad, sobre todos los grados de libertad del sistema, debe ser 1 de acuerdo con la interpretación de probabilidad. Este requisito general que debe satisfacer una función de onda se denomina condición de normalización. Dado que la función de onda tiene un valor complejo, solo se pueden medir su fase relativa y su magnitud relativa: su valor, por sí solo, no dice nada sobre las magnitudes o direcciones de los observables medibles; uno tiene que aplicar operadores cuánticos, cuyos valores propios corresponden a conjuntos de posibles resultados de mediciones, a la función de onda ψ y calcular las distribuciones estadísticas para cantidades medibles.

Antecedentes históricos

En 1900, Max Planck postuló la proporcionalidad entre la frecuencia f{displaystyle f} de un fotón y su energía E{displaystyle E}, E=hf{displaystyle E=hf.,y en 1916 la relación correspondiente entre el impulso de un fotón p{displaystyle p} y longitud de onda λ λ {displaystyle lambda }, λ λ =hp{displaystyle lambda ={frac {h}{p}},Donde h{displaystyle h} es la constante Planck. En 1923, De Broglie fue el primero en sugerir que la relación λ λ =hp{displaystyle lambda ={frac {h}{p}}, ahora llamada la relación De Broglie, espera masiva partículas, la principal pista es la invariancia de Lorentz, y esto se puede ver como el punto de partida para el desarrollo moderno de la mecánica cuántica. Las ecuaciones representan la dualidad de onda-partícula para partículas sin masa y masivas.

En las décadas de 1920 y 1930, la mecánica cuántica se desarrolló mediante el cálculo y el álgebra lineal. Entre los que utilizaron las técnicas del cálculo se encuentran Louis de Broglie, Erwin Schrödinger y otros, que desarrollaron la "mecánica ondulatoria". Quienes aplicaron los métodos del álgebra lineal incluyeron a Werner Heisenberg, Max Born y otros, y desarrollaron la "mecánica de matrices". Schrödinger demostró posteriormente que los dos enfoques eran equivalentes.

En 1926, Schrödinger publicó la famosa ecuación de onda que ahora lleva su nombre, la ecuación de Schrödinger. Esta ecuación se basó en la conservación clásica de la energía usando operadores cuánticos y las relaciones de De Broglie y las soluciones de la ecuación son las funciones de onda para el sistema cuántico. Sin embargo, nadie tenía claro cómo interpretarlo. Al principio, Schrödinger y otros pensaron que las funciones de onda representan partículas que se dispersan y la mayoría de las partículas se encuentran donde la función de onda es grande. Se demostró que esto es incompatible con la dispersión elástica de un paquete de ondas (que representa una partícula) de un objetivo; se extiende en todas direcciones. Si bien una partícula dispersa puede dispersarse en cualquier dirección, no se rompe y despega en todas las direcciones. En 1926, Born aportó la perspectiva de la amplitud de probabilidad. Esto relaciona los cálculos de la mecánica cuántica directamente con las observaciones experimentales probabilísticas. Se acepta como parte de la interpretación de Copenhague de la mecánica cuántica. Hay muchas otras interpretaciones de la mecánica cuántica. En 1927, Hartree y Fock dieron el primer paso en un intento de resolver la función de onda de N-cuerpos y desarrollaron el ciclo de autoconsistencia: un algoritmo iterativo para aproximar la solución. Ahora también se conoce como el método Hartree-Fock. El determinante y permanente de Slater (de una matriz) fue parte del método, proporcionado por John C. Slater.

Schrödinger encontró una ecuación para la función de onda que satisfacía la conservación de energía relativista antes de publicar la no relativista, pero la descartó porque predecía probabilidades negativas y energías negativas. En 1927, Klein, Gordon y Fock también lo encontraron, pero incorporaron la interacción electromagnética y demostraron que era invariante de Lorentz. De Broglie también llegó a la misma ecuación en 1928. Esta ecuación de onda relativista ahora se conoce más comúnmente como la ecuación de Klein-Gordon.

En 1927, Pauli encontró fenomenológicamente una ecuación no relativista para describir partículas de espín-1/2 en campos electromagnéticos, ahora llamada ecuación de Pauli. Pauli descubrió que la función de onda no estaba descrita por una sola función compleja de espacio y tiempo, sino que necesitaba dos números complejos, que corresponden respectivamente a los estados de espín +1/2 y −1/2 del fermión. Poco después, en 1928, Dirac encontró una ecuación de la primera unificación exitosa de la relatividad especial y la mecánica cuántica aplicada al electrón, ahora llamada ecuación de Dirac. En esto, la función de onda es un espinor representado por cuatro componentes de valor complejo: dos para el electrón y dos para la antipartícula del electrón, el positrón. En el límite no relativista, la función de onda de Dirac se asemeja a la función de onda de Pauli para el electrón. Más tarde, se encontraron otras ecuaciones de onda relativistas.

Funciones de onda y ecuaciones de onda en teorías modernas

Todas estas ecuaciones de onda tienen una importancia duradera. La ecuación de Schrödinger y la ecuación de Pauli son, en muchas circunstancias, excelentes aproximaciones de las variantes relativistas. Son considerablemente más fáciles de resolver en problemas prácticos que las contrapartes relativistas.

La ecuación de Klein-Gordon y la ecuación de Dirac, aunque son relativistas, no representan una reconciliación completa de la mecánica cuántica y la relatividad especial. La rama de la mecánica cuántica donde estas ecuaciones se estudian de la misma manera que la ecuación de Schrödinger, a menudo llamada mecánica cuántica relativista, aunque tiene mucho éxito, tiene sus limitaciones (ver, por ejemplo, Lamb shift) y problemas conceptuales (ver, por ejemplo, Dirac sea).

La relatividad hace inevitable que el número de partículas en un sistema no sea constante. Para una reconciliación completa, se necesita la teoría cuántica de campos. En esta teoría, las ecuaciones de onda y las funciones de onda tienen su lugar, pero de una manera algo diferente. Los principales objetos de interés no son las funciones de onda, sino los operadores, los llamados operadores de campo (o simplemente campos donde se entiende "operador") en el espacio de estados de Hilbert (para se describirá en la siguiente sección). Resulta que todavía se necesitan las ecuaciones de onda relativistas originales y sus soluciones para construir el espacio de Hilbert. Además, los operadores de campos libres, es decir, cuando se supone que no existen interacciones, resultan (formalmente) satisfacer la misma ecuación que los campos (funciones de onda) en muchos casos.

Así, la ecuación de Klein–Gordon (spin 0) y la ecuación de Dirac (spin 1⁄2) de esta manera permanecen en la teoría. Los análogos de espín más altos incluyen la ecuación de Proca (spin 1), la ecuación de Rarita-Schwinger (spin 3⁄2) y, de forma más general, las ecuaciones de Bargmann-Wigner. Para campos libres sin masa, dos ejemplos son la ecuación de Maxwell de campo libre (spin 1) y la ecuación de Einstein de campo libre (spin 2) para los operadores de campo. Todos ellos son esencialmente una consecuencia directa del requisito de invariancia de Lorentz. Sus soluciones deben transformarse bajo la transformación de Lorentz de una manera prescrita, es decir, bajo una representación particular del grupo de Lorentz y eso, junto con algunas otras demandas razonables, p. la propiedad de descomposición de conglomerados, con implicaciones de causalidad es suficiente para fijar las ecuaciones.

Esto se aplica a las ecuaciones de campo libre; Las interacciones no están incluidas. Si se dispone de una densidad lagrangiana (incluidas las interacciones), el formalismo lagrangiano producirá una ecuación de movimiento en el nivel clásico. Esta ecuación puede ser muy compleja y no susceptible de solución. Cualquier solución se referiría a un número fijo de partículas y no daría cuenta del término "interacción" como se hace referencia en estas teorías, que implica la creación y aniquilación de partículas y no de potenciales externos como en el "primero cuantificado" Teoría cuántica.

En la teoría de cuerdas, la situación sigue siendo análoga. Por ejemplo, una función de onda en el espacio de momento tiene el papel del coeficiente de expansión de Fourier en un estado general de una partícula (cuerda) con momento que no está claramente definido.

Definición (una partícula sin espín en una dimensión)

Olas permanentes para una partícula en una caja, ejemplos de estados estacionarios.

Olas itinerantes de una partícula libre.

Las partes reales de la función de onda de posición Ψx) y función de onda de impulso Negotiat(p), y densidades de probabilidad correspondientes ←x)² y CCPR/p)², para una partícula spin-0 en una x o p dimensión. La opacidad del color de las partículas corresponde a la densidad de probabilidad (no la función de onda) de encontrar la partícula en posición x o impulso p.

Por ahora, considere el caso simple de una sola partícula no relativista, sin espín, en una dimensión espacial. A continuación se analizan casos más generales.

Funciones de onda de posición-espacio

El estado de tal partícula está completamente descrito por su función de onda,

Ψ Ψ ()x,t),{displaystyle Psi (x,t),}

Para una partícula sin espín en una dimensión, si la función de onda se interpreta como una amplitud de probabilidad, el módulo cuadrado de la función de onda, el número real positivo

SilencioΨ Ψ ()x,t)Silencio2=Ψ Ψ Alternativa Alternativa ()x,t)Ψ Ψ ()x,t)=*** *** ()x,t),{displaystyle left durablePsi (x,t)right sometida^{2}= Psi ^{*}(x,t)Psi (x,t)=rho (x,t),}

Condición de normalización

La probabilidad de que su posición x esté en el intervalo a ≤ x ≤ b es la integral de la densidad en este intervalo:

Pa≤ ≤ x≤ ≤ b()t)=∫ ∫ abSilencioΨ Ψ ()x,t)Silencio2dx{displaystyle P_{aleq xleq b}(t)=int _{a}^{b}, pacienciaPsi (x,t)

∫ ∫ − − JUEGO JUEGO JUEGO JUEGO SilencioΨ Ψ ()x,t)Silencio2dx=1,{displaystyle int _{-infty }infty }, sometidaPsi (x,t) habit^{2}dx=1,}

Para un sistema dado, el conjunto de todas las posibles funciones de onda normalizables (en cualquier momento dado) forma un espacio vectorial matemático abstracto, lo que significa que es posible sumar diferentes funciones de onda y multiplicar funciones de onda por números complejos (ver espacio vectorial para detalles). Técnicamente, debido a la condición de normalización, las funciones de onda forman un espacio proyectivo en lugar de un espacio vectorial ordinario. Este espacio vectorial es de dimensión infinita, porque no hay un conjunto finito de funciones que se puedan sumar en varias combinaciones para crear todas las funciones posibles. Además, es un espacio de Hilbert, porque el producto interno de dos funciones de onda Ψ₁ y Ψ ₂ se puede definir como el número complejo (en el tiempo t)

()Ψ Ψ 1,Ψ Ψ 2)=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO Ψ Ψ 1Alternativa Alternativa ()x,t)Ψ Ψ 2()x,t)dx.{displaystyle (Psi _{1},Psi _{2})=int _{-infty }{infty },Psi _{1}{*}(x,t)Psi _{2}(x,t)dx.}

Más detalles se dan a continuación. Aunque el producto interno de dos funciones de onda es un número complejo, el producto interno de una función de onda Ψ consigo mismo,

()Ψ Ψ ,Ψ Ψ )=.. Ψ Ψ .. 2,{displaystyle (PsiPsi)= Psi sobrevivir.

Si (Ψ, Ψ) = 1, entonces Ψ se normaliza. Si Ψ no está normalizado, al dividir por su norma se obtiene la función normalizada Ψ/||Ψ||. Dos funciones de onda Ψ₁ y Ψ₂ son ortogonales si (Ψ₁, Ψ₂) = 0. Si están normalizados y ortogonales, son ortonormales. La ortogonalidad (y por lo tanto también la ortonormalidad) de las funciones de onda no es una condición necesaria que las funciones de onda deban satisfacer, pero es instructivo considerarlo ya que esto garantiza la independencia lineal de las funciones. En una combinación lineal de funciones de onda ortogonales Ψ_n tenemos,

Ψ Ψ =.. nanΨ Ψ n,an=()Ψ Ψ n,Ψ Ψ )()Ψ Ψ n,Ψ Ψ n){displaystyle Psi =sum ¿Qué? ¿Por qué?

Si las funciones de onda Ψ_n fueran no ortogonales, los coeficientes serían menos simples de obtener.

Estados cuánticos como vectores

En la interpretación de Copenhague, el módulo al cuadrado del producto interior (un número complejo) da un número real

Silencio()Ψ Ψ 1,Ψ Ψ 2)Silencio2=P()Ψ Ψ 2→ → Ψ Ψ 1),{displaystyle left WordPress(Psi _{1},Psi _{2})right WordPress^{2}=Pleft(Psi) ¿Qué? Psi _{1}right),}

En un instante particular de tiempo, todos los valores de la función de onda Ψ(x, t) son componentes de un vector Hay innumerables infinitos de ellos y la integración se usa en lugar de la suma. En notación Bra-ket, este vector se escribe

SilencioΨ Ψ ()t).. =∫ ∫ Ψ Ψ ()x,t)Silenciox.. dx{displaystyle ¦Psi (t)rangle =int Psi (x,t)

• Todas las poderosas herramientas de álgebra lineal se pueden utilizar para manipular y comprender las funciones de onda. Por ejemplo:
  • Álgebra lineal explica cómo un espacio vectorial puede ser dado una base, y luego cualquier vector en el espacio vectorial se puede expresar en esta base. Esto explica la relación entre una función de onda en el espacio de posición y una función de onda en el espacio de impulso y sugiere que también hay otras posibilidades.
  • La notación de frenos se puede utilizar para manipular las funciones de onda.
• La idea de que los estados cuánticos son vectores en un espacio vectorial abstracto es completamente general en todos los aspectos de la mecánica cuántica y la teoría del campo cuántico, mientras que la idea de que los estados cuánticos son funciones de "onda" de valor complejo es sólo verdad en ciertas situaciones.

El parámetro de tiempo a menudo se suprime y estará en lo siguiente. La coordenada x es un índice continuo. Los |x⟩ son los vectores base, que son ortonormales, por lo que su producto interno es un delta función;

.. x.Silenciox.. =δ δ ()x.− − x){displaystyle langle x'tenciónxrangle =delta (x'-x)}

.. x.SilencioΨ Ψ .. =∫ ∫ Ψ Ψ ()x).. x.Silenciox.. dx=Ψ Ψ ()x.){displaystyle langle x'standingPsi rangle =int Psi (x)langle x'prehensixrangle dx=Psi (x')}

SilencioΨ Ψ .. =∫ ∫ Silenciox.. .. xSilencioΨ Ψ .. dx=()∫ ∫ Silenciox.. .. xSilenciodx)SilencioΨ Ψ .. {displaystyle TENIDOPsi rangle =int TENXrangle langle x 64Psi rangle dx=left(int TENXrangle langle x soportadxright)

I=∫ ∫ Silenciox.. .. xSilenciodx.{displaystyle I=int Silencioxrangle langle x sometidadx,}

Encontrar el operador de identidad en una base permite que el estado abstracto se exprese explícitamente en una base y más (el producto interno entre dos vectores de estado y otros operadores para observables se pueden expresar en la base).

Funciones de onda impulso-espacio

La partícula también tiene una función de onda en el espacio de cantidad de movimiento:

CCPR CCPR ()p,t){displaystyle Phi (p,t)}

Análogo al caso de posición, el producto interno de dos funciones de onda Φ₁(p, t) y Φ₂(p, t) se pueden definir como:

()CCPR CCPR 1,CCPR CCPR 2)=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO CCPR CCPR 1Alternativa Alternativa ()p,t)CCPR CCPR 2()p,t)dp.{displaystyle (Phi _{1},Phi _{2})=int _{-infty }{infty },\__{1}{*}(p,t)Phi _{2}(p,t)dp,}

Una solución particular a la ecuación de Schrödinger independiente del tiempo es

Ψ Ψ p()x)=eipx/▪ ▪ ,{displaystyle Psi _{p}(x)=e^{ipx/hbar }}

{}Ψ Ψ p()x,t),− − JUEGO JUEGO ≤ ≤ p≤ ≤ JUEGO JUEGO }{displaystyle {Psi _{p}(x,t),-infty leq pleq infty }}

()Ψ Ψ p,Ψ Ψ p.)=δ δ ()p− − p.).{displaystyle (Psi _{p},Psi _{p'})=delta (p-p').}

Por otro lado, aunque son linealmente independientes, hay demasiados (forman un conjunto incontable) para una base para el espacio físico de Hilbert. Todavía se pueden usar para expresar todas las funciones en él usando transformadas de Fourier como se describe a continuación.

Relaciones entre las representaciones de posición y momento

Las representaciones x y p son

SilencioΨ Ψ .. =ISilencioΨ Ψ .. =∫ ∫ Silenciox.. .. xSilencioΨ Ψ .. dx=∫ ∫ Ψ Ψ ()x)Silenciox.. dx,SilencioΨ Ψ .. =ISilencioΨ Ψ .. =∫ ∫ Silenciop.. .. pSilencioΨ Ψ .. dp=∫ ∫ CCPR CCPR ()p)Silenciop.. dp.{displaystyle {begin{aligned} Psi rangle =I WordPressPsi rangle >int tenciónxrangle langle x sufrimientoPsi rangle dx=int Psi (x) WordPressxrangle dx,\\Psi rangle =I durablePsi rangle <=int Ненели перитеный }

Ahora tome la proyección del estado Ψ sobre las funciones propias de la cantidad de movimiento usando la última expresión en las dos ecuaciones,

∫ ∫ Ψ Ψ ()x).. pSilenciox.. dx=∫ ∫ CCPR CCPR ()p.).. pSilenciop... dp.=∫ ∫ CCPR CCPR ()p.)δ δ ()p− − p.)dp.=CCPR CCPR ()p).{displaystyle int Psi (x)langle p sometidaxrangle dx=int Phi (p')langle p sometidap'rangle dp'=int Phi (p')delta (p-p')dp'=Phi (p).}

Luego, utilizando la expresión conocida para estados propios adecuadamente normalizados del impulso en las soluciones de representación de posición de la ecuación libre de Schrödinger

.. xSilenciop.. =p()x)=12π π ▪ ▪ ei▪ ▪ px⇒ ⇒ .. pSilenciox.. =12π π ▪ ▪ e− − i▪ ▪ px,{displaystyle langle x WordPressprangle =p(x)={frac {1}{sqrt {2pihbar }e^{frac} {i}{hbar }px}Rightarrow langle p sometidaxrangle ={frac} {1}{sqrt [2pihbar]}e^{-{frac {}px}

CCPR CCPR ()p)=12π π ▪ ▪ ∫ ∫ Ψ Ψ ()x)e− − i▪ ▪ pxdx.{displaystyle Phi (p)={frac {1}{sqrt {2pihbar }}int Psi (x)e^{-{frac {i}px}dx,}

Del mismo modo, usando funciones propias de posición,

Ψ Ψ ()x)=12π π ▪ ▪ ∫ ∫ CCPR CCPR ()p)ei▪ ▪ pxdp.{displaystyle Psi (x)={frac {1}{sqrt {2pihbar }}int Phi (p)e^{frac {i}{hbar }px}dp,}

Se encuentra que las funciones de onda espacio-posición y espacio-momento son transformadas de Fourier entre sí. Las dos funciones de onda contienen la misma información, y cualquiera de ellas por sí sola es suficiente para calcular cualquier propiedad de la partícula. Como representantes de elementos del espacio físico abstracto de Hilbert, cuyos elementos son los posibles estados del sistema bajo consideración, representan el mismo vector de estado, por lo tanto, estados físicos idénticos, pero generalmente no son iguales cuando se ven como Funciones cuadradas integrables.

En la práctica, la función de onda espacio-posición se usa con mucha más frecuencia que la función de onda espacio-momento. El potencial que entra en la ecuación relevante (Schrödinger, Dirac, etc.) determina en qué base la descripción es más fácil. Para el oscilador armónico, x y p ingrese simétricamente, por lo que allí no importa qué descripción se use. Se obtiene la misma ecuación (constantes de módulo). De esto, con un poco de reflexión, se deduce que las soluciones a la ecuación de onda del oscilador armónico son funciones propias de la transformada de Fourier en L².

Definiciones (otros casos)

Las siguientes son las formas generales de la función de onda para sistemas en dimensiones más altas y más partículas, además de incluir otros grados de libertad además de las coordenadas de posición o los componentes de momento.

Estados de una partícula en el espacio de posición 3D

La función de onda del espacio de posición de una sola partícula sin espín en tres dimensiones espaciales es similar al caso de una dimensión espacial anterior:

Ψ Ψ ()r,t){displaystyle Psi (mathbf {r}t)}

SilencioΨ Ψ ()t).. =∫ ∫ d3rΨ Ψ ()r,t)Silencior.. {displaystyle ¦Psi (t)rangle =int d^{3}!mathbf {r} ,Psi (mathbf {r}t), sometidamathbf {r} rangle }

Todos los comentarios anteriores sobre productos internos, funciones de onda espacial de cantidad de movimiento, transformadas de Fourier, etc., se extienden a dimensiones superiores.

Para una partícula con espín, ignorando los grados de libertad de posición, la función de onda es una función de espín solamente (el tiempo es un parámetro);

.. ()sz,t){displaystyle xi (s_{z},t)}

.. =[.. ()s,t).. ()s− − 1,t)⋮ ⋮ .. ()− − ()s− − 1),t).. ()− − s,t)]=.. ()s,t)[10⋮ ⋮ 00]+.. ()s− − 1,t)[01⋮ ⋮ 00]+⋯ ⋯ +.. ()− − ()s− − 1),t)[00⋮ ⋮ 10]+.. ()− − s,t)[00⋮ ⋮ 01]{fnMicrosoft Sans Serif}

En notación bra-ket, estos se organizan fácilmente en los componentes de un vector

Silencio.. ()t).. =.. sz=− − ss.. ()sz,t)Silenciosz.. {displaystyle TENIDOxi (t)rangle =sum ¿Por qué?

El vector completo ξ es una solución de la ecuación de Schrödinger (con un hamiltoniano adecuado), que se despliega en un sistema acoplado de 2s + 1 ecuaciones diferenciales ordinarias con soluciones ξ(s, t), ξ(s − 1, t),..., ξ(−s, t). El término "función de giro" en lugar de "función de onda" es utilizado por algunos autores. Esto contrasta las soluciones a las funciones de onda espacial de posición, siendo las coordenadas de posición grados de libertad continuos, porque entonces la ecuación de Schrödinger toma la forma de una ecuación de onda.

Más generalmente, para una partícula en 3D con cualquier giro, la función de onda se puede escribir en "espacio de posición-giro" como:

Ψ Ψ ()r,sz,t){displaystyle Psi (mathbf {r}s_{z},t)}

Ψ Ψ ()r,t)=[Ψ Ψ ()r,s,t)Ψ Ψ ()r,s− − 1,t)⋮ ⋮ Ψ Ψ ()r,− − ()s− − 1),t)Ψ Ψ ()r,− − s,t)]{begin{bmatrix}Psi (mathbf {r}s,t)\\\psi (mathbf {r}s,t)\psi (mathbf {r}s-1,t)vdots\\\psi (mathbf {cH00}cH0cH00cH00cH0}cH00cH00cH00cH00cH009cH00cH00cH00cH00cH00cH009cH00cH00cH00cH00cH009cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}cH009cH00cH00}cH009cH00cH00}cH00cH

Todos los valores de la función de onda, no solo para variables discretas sino también continuas, se reúnen en un solo vector

SilencioΨ Ψ ()t).. =.. sz∫ ∫ d3rΨ Ψ ()r,sz,t)Silencior,sz.. {displaystyle ¦Psi (t)rangle =sum _{s_{z}int d^{3}!mathbf {r} ,Psi (mathbf {r}s_{z},t), eternamentemathbf {r}s_{z}rangle }

Para una sola partícula, el producto tensorial ⊗ de su vector de estado de posición |ψ ⟩ y girar el vector de estado |ξ⟩ da el vector de estado de giro de posición compuesto

Silencio↑ ↑ ()t).. ⊗ ⊗ Silencio.. ()t).. =.. sz∫ ∫ d3r↑ ↑ ()r,t).. ()sz,t)Silencior.. ⊗ ⊗ Silenciosz.. {displaystyle Нpsi (t)rangle !otimes !

SilencioΨ Ψ ()t).. =Silencio↑ ↑ ()t).. ⊗ ⊗ Silencio.. ()t).. {displaystyle tenciónPsi (t)rangle = sufrimientopsi (t)rangle !otimes !

Ψ Ψ ()r,sz,t)=↑ ↑ ()r,t).. ()sz,t){displaystyle Psi (mathbf {r}s_{z},t)=psi (mathbf {r}t),xi (s_{z},t)}

Silencior,sz.. =Silencior.. ⊗ ⊗ Silenciosz.. {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} rangle !otimes !

La factorización del producto tensorial solo es posible si los momentos angulares orbital y de espín de la partícula son separables en el operador hamiltoniano que subyace a la dinámica del sistema (en otras palabras, el hamiltoniano se puede dividir en la suma de orbital y términos de espín). La dependencia del tiempo se puede ubicar en cualquiera de los factores, y la evolución temporal de cada uno se puede estudiar por separado. La factorización no es posible para aquellas interacciones donde un campo externo o cualquier cantidad dependiente del espacio se acopla al espín; los ejemplos incluyen una partícula en un campo magnético y el acoplamiento espín-órbita.

La discusión anterior no se limita al giro como una variable discreta, también se puede usar el momento angular total J. Otros grados discretos de libertad, como isospin, pueden expresarse de manera similar al caso de spin anterior.

Estados de muchas partículas en el espacio de posición 3d

Olas de viaje de dos partículas libres, con dos de tres dimensiones suprimidas. La parte superior es la función de onda de posición-espacio, el fondo es la función de onda de impulso-espacio, con densidades de probabilidad correspondientes.

Si hay muchas partículas, en general solo hay una función de onda, no una función de onda separada para cada partícula. El hecho de que una función de onda describa muchas partículas es lo que hace posible el entrelazamiento cuántico y la paradoja EPR. La función de onda de posición-espacio para partículas N se escribe:

Ψ Ψ ()r1,r2⋯ ⋯ rN,t){displaystyle Psi (mathbf {r} _{1},mathbf {r} _{2}cdots mathbf {r} _{N},t)}

En mecánica cuántica existe una distinción fundamental entre partículas idénticas y partículas distinguibles. Por ejemplo, dos electrones cualesquiera son idénticos y fundamentalmente indistinguibles entre sí; las leyes de la física hacen imposible "sellar un número de identificación" en un determinado electrón para seguirle la pista. Esto se traduce en un requisito sobre la función de onda para un sistema de partículas idénticas:

Ψ Ψ ()...... ra,...... ,rb,...... )=± ± Ψ Ψ ()...... rb,...... ,ra,...... ){displaystyle Psi left(ldots mathbf {r} _{a},ldotsmathbf {r} _{b},ldots right)=pm Psi left(ldots mathbf {r} _{b},ldotsmathbf {r}

Para partículas N distinguibles (no hay dos que sean idénticas, es decir, no hay dos que tengan el mismo conjunto de números cuánticos), no es necesario que la función de onda sea simétrica o antisimétrica.

Para una colección de partículas, algunas idénticas con coordenadas r₁, r₂ ,... y otros distinguibles x₁, x₂,... (no idénticos entre sí, y no idénticos a las partículas idénticas antes mencionadas), la función de onda es simétrica o antisimétrica en las coordenadas de partículas idénticas r_i solamente:

Ψ Ψ ()...... ra,...... ,rb,...... ,x1,x2,...... )=± ± Ψ Ψ ()...... rb,...... ,ra,...... ,x1,x2,...... ){displaystyle {fnMicrosoft Sans Serif}

Nuevamente, no existe un requisito de simetría para las coordenadas de partículas distinguibles x_i.

La función de onda para N partículas cada una con espín es la función de valores complejos

Ψ Ψ ()r1,r2⋯ ⋯ rN,sz1,sz2⋯ ⋯ szN,t){displaystyle Psi (mathbf {r} _{1},mathbf {r} _{2}cdots mathbf {r} ¿Qué?

Al acumular todos estos componentes en un solo vector,

SilencioΨ Ψ .. =.. sz1,...... ,szN⏞ ⏞ Etiquetas discretas∫ ∫ RNd3rN⋯ ⋯ ∫ ∫ R1d3r1⏞ ⏞ Etiquetas continuasΨ Ψ ()r1,...... ,rN,sz1,...... ,szN)⏟ ⏟ función de onda (componente devector estatal a lo largo del estado de base)Silencior1,...... ,rN,sz1,...... ,szN.. ⏟ ⏟ estado de base (basis ket).{displaystyle SilencioPsi rangle =overbrace {sum ################################################################################################################################################################################################################################################################ ¿Qué? _{N}cdots int ¿Qué? ################################################################################################################################################################################################################################################################ ¿Qué? {begin{c}{text{wave function (component of }\{text{ state vector along basis state)}}end{array}};underbrace { actualmathbf {r} _{1},ldotsmathbf {r} ¿Por qué?

Para partículas idénticas, los requisitos de simetría se aplican a los argumentos de posición y giro de la función de onda para que tenga la simetría general correcta.

Las fórmulas para los productos internos son integrales sobre todas las coordenadas o momentos y sumas sobre todos los números cuánticos de espín. Para el caso general de partículas N con espín en 3-d,

()Ψ Ψ 1,Ψ Ψ 2)=.. szN⋯ ⋯ .. sz2.. sz1∫ ∫ allspaced3r1∫ ∫ allspaced3r2⋯ ⋯ ∫ ∫ allspaced3rNΨ Ψ 1Alternativa Alternativa ()r1⋯ ⋯ rN,sz1⋯ ⋯ szN,t)Ψ Ψ 2()r1⋯ ⋯ rN,sz1⋯ ⋯ szN,t){displaystyle (Psi _{1},Psi _{2}=sum - ¿Qué? sum - ¿Qué? _{s_{z,1}intlimits _{mathrm {all,space}d^{3}mathbf {r} _{1}int limits _{mathrm {all,space} }d^{3}mathbf {r} _{2}cdots int limits _{mathrm {all,space} }d^{3}mathbf {r} ¿Por qué? ¿Por qué? ¿Qué?

Las transformadas multidimensionales de Fourier de las funciones de onda espacial de posición o posición-giro generan funciones de onda espacial de momento o de momento-giro.

Interpretación de probabilidad

Para el caso general de N partículas con espín en 3d, si Ψ se interpreta como una amplitud de probabilidad, la densidad de probabilidad es

*** *** ()r1⋯ ⋯ rN,sz1⋯ ⋯ szN,t)=SilencioΨ Ψ ()r1⋯ ⋯ rN,sz1⋯ ⋯ szN,t)Silencio2{displaystyle rho left(mathbf {r} _{1}cdots mathbf {r} _{N},s_{z,1}cdots s_{z,N}=left durablePsi left(mathbf {r} _{1}cdots mathbf {r} ¿Qué?

y la probabilidad de que la partícula 1 esté en la región R₁ con espín s_z1 = m₁ y la partícula 2 está en la región R₂ con espín s _z2 = m₂ etc. en el tiempo t es la integral de la densidad de probabilidad sobre estas regiones y se evalúa en estos números de espín:

Pr1▪ ▪ R1,sz1=m1,...... ,rN▪ ▪ RN,szN=mN()t)=∫ ∫ R1d3r1∫ ∫ R2d3r2⋯ ⋯ ∫ ∫ RNd3rNSilencioΨ Ψ ()r1⋯ ⋯ rN,m1⋯ ⋯ mN,t)Silencio2{displaystyle P_{mathbf {r} {cH00} R_{1},s_{z,1}=m_{1},ldotsmathbf {r} ¿Qué? R_{N},s_{z,N}=m_{N}(t)=int ¿Por qué? ¿Qué? ¿Qué? _{N}cdots mathbf {r} ¿Qué? - ¿Qué?

Dependencia del tiempo

Para sistemas en potenciales independientes del tiempo, la función de onda siempre puede escribirse como una función de los grados de libertad multiplicados por un factor de fase dependiente del tiempo, cuya forma viene dada por la ecuación de Schrödinger. Para partículas N, considerando solo sus posiciones y suprimiendo otros grados de libertad,

Ψ Ψ ()r1,r2,...... ,rN,t)=e− − iEt/▪ ▪ ↑ ↑ ()r1,r2,...... ,rN),{fnMicrosoft Sans Serif}

La dependencia temporal del estado cuántico y los operadores se puede ubicar de acuerdo con transformaciones unitarias en los operadores y estados. Para cualquier estado cuántico |Ψ⟩ y operador O, en la imagen de Schrödinger |Ψ(t)⟩ cambia con el tiempo según la ecuación de Schrödinger mientras O es constante. En la imagen de Heisenberg es al revés, |Ψ⟩ es constante mientras que O(t) evoluciona con el tiempo de acuerdo con la ecuación de movimiento de Heisenberg. La imagen de Dirac (o interacción) es intermedia, la dependencia del tiempo se da tanto en los operadores como en los estados que evolucionan de acuerdo con las ecuaciones de movimiento. Es útil principalmente para calcular elementos de matriz S.

Ejemplos no relativistas

Las siguientes son soluciones a la ecuación de Schrödinger para una partícula sin espín no relativista.

Barrera de potencial finito

Escalada en una barrera potencial finita de altura V₀. Se indican las amplitudes y la dirección de las ondas móviles izquierda y derecha. En rojo, esas olas utilizadas para la derivación de la amplitud de reflexión y transmisión. E ■ V₀ para esta ilustración.

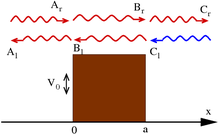
Una de las características más destacadas de la mecánica ondulatoria es la posibilidad de que una partícula alcance un lugar con un potencial de fuerza prohibitivo (en la mecánica clásica). Un modelo común es la "barrera potencial", el caso unidimensional tiene el potencial

Funciones de onda de electrones confinadas 3D en un punto cuántico. Aquí se muestran puntos cuánticos rectangulares y triangulares. Los estados de energía en puntos rectangulares son más tipo s y tipo p. Sin embargo, en un punto triangular las funciones de onda se mezclan debido a la simetría del confinamiento. (Haga clic para la animación)

En un cristalito semiconductor cuyo radio es más pequeño que el tamaño del radio de Bohr de su excitón, los excitones se comprimen, lo que lleva a un confinamiento cuántico. Luego, los niveles de energía se pueden modelar utilizando el modelo de partículas en una caja en el que la energía de los diferentes estados depende de la longitud de la caja.

Oscilador armónico cuántico

Las funciones de onda para el oscilador armónico cuántico se pueden expresar en términos de polinomios de Hermite H_n, son

Ψ Ψ n()x)=12nn!⋅ ⋅ ()m⋅ ⋅ π π ▪ ▪ )1/4⋅ ⋅ e− − m⋅ ⋅ x22▪ ▪ ⋅ ⋅ Hn()m⋅ ⋅ ▪ ▪ x){displaystyle Psi _{n}(x)={sqrt {frac {1}{2^{n},n}}cdot left({frac {momega {fnMicrosoft Sans Serif} {cdot e^{-{frac {momega ¿Qué?

La densidad de probabilidad de electrones para los primeros pocos electrones de hidrógeno se muestra como secciones transversales. Estos orbitales forman una base ortonormal para la función de onda del electrón. Diferentes órbitas se representan con diferente escala.

átomo de hidrógeno

Las funciones de onda de un electrón en un átomo de hidrógeno se expresan en términos de armónicos esféricos y polinomios de Laguerre generalizados (diferentes autores los definen de manera diferente; consulte el artículo principal sobre ellos y el átomo de hidrógeno).

Es conveniente utilizar coordenadas esféricas, y la función de onda se puede separar en funciones de cada coordenada,

Ψ Ψ nl l m()r,Silencio Silencio ,φ φ )=R()r)Yl l m()Silencio Silencio ,φ φ ){displaystyle Psi _{nell m}(r,thetaphi)=R(r),,Y_{ell }^{m}!(thetaphi)}

Ψ Ψ nl l m()r,Silencio Silencio ,φ φ )=()2na0)3()n− − l l − − 1)!2n[()n+l l )!]e− − r/na0()2rna0)l l Ln− − l l − − 12l l +1()2rna0)⋅ ⋅ Yl l m()Silencio Silencio ,φ φ ){displaystyle {fnnfnell m} {fnnfnnfnh}}nnnn}} {nnn}}}}}} {fn} {fn-n-ell -1)}{2n[n+ell]}}}}}}}}}}}}}}}}}} {cccccc]cccccccc]ccccc}ccccccccccccccccccccccccccccc]ccc]ccccnccccccccccccccccccccccccc Vale.

Esta solución no tiene en cuenta el giro del electrón.

En la figura de los orbitales de hidrógeno, las 19 subimágenes son imágenes de funciones de onda en el espacio de posición (su norma al cuadrado). Las funciones de onda representan el estado abstracto caracterizado por el triple de números cuánticos (n, ℓ, m) , en la parte inferior derecha de cada imagen. Estos son el número cuántico principal, el número cuántico del momento angular orbital y el número cuántico magnético. Junto con un número cuántico de proyección de espín del electrón, este es un conjunto completo de observables.

La figura puede servir para ilustrar algunas propiedades adicionales de los espacios de funciones de las funciones de onda.

• En este caso, las funciones de onda son cuadradas integradoras. Uno puede inicialmente tomar el espacio de función como el espacio de funciones integradas cuadradas, generalmente denotadas L2.
• Las funciones mostradas son soluciones a la ecuación Schrödinger. Obviamente, no todas las funciones en L² satisface la ecuación Schrödinger para el átomo de hidrógeno. El espacio de función es por lo tanto un subespacio L².
• Las funciones mostradas forman parte de una base para el espacio de función. A cada triple ()n, l, m), allí corresponde una función de onda base. Si se tiene en cuenta el giro, hay dos funciones básicas para cada triple. El espacio de función tiene una base contable.
• Las funciones de base son mutuamente ortonormales.

Funciones de onda y espacios de funciones

El concepto de espacios de funciones entra naturalmente en la discusión sobre las funciones de onda. Un espacio de funciones es un conjunto de funciones, generalmente con algunos requisitos definitorios sobre las funciones (en el presente caso, que sean integrables al cuadrado), a veces con una estructura algebraica en el conjunto (en el presente caso, una estructura de espacio vectorial con un producto interno), junto con una topología en el conjunto. Este último se usará escasamente aquí, solo se necesita para obtener una definición precisa de lo que significa que un subconjunto de un espacio funcional esté cerrado. Se concluirá a continuación que el espacio funcional de las funciones de onda es un espacio de Hilbert. Esta observación es el fundamento de la formulación matemática predominante de la mecánica cuántica.

Estructura del espacio vectorial

Una función de onda es un elemento de un espacio funcional caracterizado en parte por las siguientes descripciones concretas y abstractas.

• La ecuación Schrödinger es lineal. Esto significa que las soluciones a ella, las funciones de onda, pueden ser agregadas y multiplicadas por los escalares para formar una nueva solución. El conjunto de soluciones a la ecuación Schrödinger es un espacio vectorial.
• El principio de superposición de la mecánica cuántica. Si Ψ y CCPR son dos estados en el espacio abstracto estados de un sistema mecánico cuántico, y a y b son dos números complejos, entonces aΨ + bCCPR es un estado válido también. (Si el vector nulo cuenta como un estado válido ("ningún sistema presente") es una cuestión de definición. El vector nulo lo hace no en cualquier tipo describir el estado de vacío en la teoría del campo cuántico.) El conjunto de estados permitidos es un espacio vectorial.

Esta similitud, por supuesto, no es accidental. También hay una distinción entre los espacios a tener en cuenta.

Representaciones

Los estados básicos se caracterizan por un conjunto de números cuánticos. Este es un conjunto de valores propios de un conjunto máximo de observables conmutables. Los observables físicos están representados por operadores lineales, también llamados observables, en el espacio vectorial. Maximalidad significa que no se pueden agregar al conjunto más observables algebraicamente independientes que conmuten con los ya presentes. Una elección de tal conjunto puede llamarse una elección de representación.

• Es un postulado de la mecánica cuántica que una cantidad físicamente observable de un sistema, como posición, impulso o giro, está representado por un operador hermitiano lineal en el espacio estatal. Los posibles resultados de la medición de la cantidad son los eigenvalues del operador. A un nivel más profundo, la mayoría de los observables, tal vez todos, surgen como generadores de simetrías.
• La interpretación física es que tal conjunto representa lo que puede – en teoría – simultáneamente medirse con precisión arbitraria. La relación de incertidumbre Heisenberg prohíbe mediciones exactas simultáneas de dos observables no transmutadores.
• El set no es único. Puede para un sistema de una partícula, por ejemplo, ser posición y giro z- proyección, ()x, S_z), o puede ser impulso y giro Sí.- proyección, ()p, S_Sí.). En este caso, el operador correspondiente a la posición (un operador de multiplicación en la representación de posición) y el operador correspondiente al impulso (un operador diferencial en la representación de posición) no se comunican.
• Una vez que se elige una representación, todavía hay arbitrariedad. Queda por elegir un sistema de coordenadas. Esto puede, por ejemplo, corresponder a una elección x, Sí.- y z-eje, o una opción coordenadas curvilinear como ejemplificado por las coordenadas esféricas utilizadas para las funciones de onda atómica de hidrógeno. Esta elección final también fija una base en el espacio abstracto de Hilbert. Los estados básicos son etiquetados por los números cuánticos correspondientes al conjunto máximo de observables de conmutación y un sistema de coordinación adecuado.

Los estados abstractos son "abstract" sólo en que no se da una elección arbitraria necesaria para una descripción explícita particular. Esto es lo mismo que decir que no se ha dado ninguna opción de conjunto máximo de observables conmutables. Esto es análogo a un espacio vectorial sin una base específica. En consecuencia, las funciones de onda correspondientes a un estado no son únicas. Esta no unicidad refleja la no unicidad en la elección de un conjunto máximo de observables conmutables. Para una partícula de espín en una dimensión, a un estado particular le corresponden dos funciones de onda, Ψ(x, S_z) y Ψ(p, S_y ), ambos describen el mismo estado.

• Para cada elección de conjuntos máximos de conmutación de observables para el espacio estatal abstracto, hay una representación correspondiente que se asocia a un espacio de función de las funciones de onda.
• Entre todos estos diferentes espacios de función y el espacio estatal abstracto, hay correspondencias únicas (aquí ignorando la normalización y los factores de fase inservibles), el denominador común aquí es un estado abstracto particular. La relación entre el impulso y las funciones de onda espacial de posición, por ejemplo, describir el mismo estado es la transformación Fourier.

Cada elección de representación debe considerarse como la especificación de un espacio funcional único en el que viven las funciones de onda correspondientes a esa elección de representación. Es mejor mantener esta distinción, incluso si se pudiera argumentar que dos espacios de funciones de este tipo son matemáticamente iguales, p. siendo el conjunto de funciones cuadradas integrables. Entonces se puede pensar en los espacios de funciones como dos copias distintas de ese conjunto.

Producto interior

Hay una estructura algebraica adicional en los espacios vectoriales de funciones de onda y el espacio de estado abstracto.

• Físicamente, se interpretan diferentes funciones de onda para superponerse hasta cierto punto. Un sistema en un estado Ψ que hace no superposición con un estado CCPR no se puede encontrar en el estado CCPR a medida. Pero si CCPR₁, ⋅₂,... sola Ψ a algunos grado, existe la posibilidad de que la medición de un sistema descrito por Ψ se encontrará en estados CCPR₁, ⋅₂,.... También se aplican reglas de selección. Estos son generalmente formulados en la preservación de algunos números cuánticos. Esto significa que ciertos procesos permitidos desde algunas perspectivas (por ejemplo, la conservación de la energía y el impulso) no ocurren porque la inicial y la final total Las funciones de onda no se superponen.
• Matemáticamente, resulta que las soluciones a la ecuación Schrödinger para potenciales particulares son ortogonal de alguna manera, esto se describe generalmente por una integral
  ∫ ∫ Ψ Ψ mAlternativa Alternativa Ψ Ψ nwdV=δ δ nm,{displaystyle int Psi ¿Qué? ¿Qué? ¿Qué?

  
  Donde m, n son (conjuntos de) índices (números cuánticos) etiquetando diferentes soluciones, la función estrictamente positiva w se llama una función de peso, y δ_mn es el Kronecker delta. La integración se lleva a cabo en todo el espacio pertinente.

Esto motiva la introducción de un producto interior en el espacio vectorial de estados cuánticos abstractos, compatible con las observaciones matemáticas anteriores al pasar a una representación. Se denota (Ψ, Φ), o en la notación Bra–ket ⟨Ψ|Φ⟩. Produce un número complejo. Con el producto interior, el espacio funcional es un espacio de producto interior. La apariencia explícita del producto interno (generalmente una integral o una suma de integrales) depende de la elección de la representación, pero el número complejo (Ψ, Φ) no. Gran parte de la interpretación física de la mecánica cuántica se deriva de la regla de Born. Establece que la probabilidad p de encontrar al medir el estado Φ dada la el sistema está en el estado Ψ es

p=Silencio()CCPR CCPR ,Ψ Ψ )Silencio2,{fnMicrosoft Sans Serif}

Espacio de Hilbert

Las observaciones anteriores encapsulan la esencia de los espacios de funciones de los cuales las funciones de onda son elementos. Sin embargo, la descripción aún no está completa. Existe un requisito técnico adicional sobre el espacio funcional, el de la completitud, que permite tomar límites de secuencias en el espacio funcional y asegurarse de que, si el límite existe, es un elemento del espacio funcional. Un espacio de producto interior completo se llama espacio de Hilbert. La propiedad de completitud es crucial en los tratamientos y aplicaciones avanzados de la mecánica cuántica. Por ejemplo, la existencia de operadores de proyección o proyecciones ortogonales se basa en la integridad del espacio. Estos operadores de proyección, a su vez, son esenciales para la declaración y prueba de muchos teoremas útiles, p. el teorema espectral No es muy importante en la introducción a la mecánica cuántica, y los detalles técnicos y los enlaces se pueden encontrar en notas a pie de página como la siguiente. El espacio L² es un espacio de Hilbert, con el producto interior presentado más adelante. El espacio funcional del ejemplo de la figura es un subespacio de L². Un subespacio de un espacio de Hilbert es un espacio de Hilbert si es cerrado.

En resumen, el conjunto de todas las posibles funciones de onda normalizables para un sistema con una elección particular de base, junto con el vector nulo, constituyen un espacio de Hilbert.

No todas las funciones de interés son elementos de algún espacio de Hilbert, digamos L². El ejemplo más evidente es el conjunto de funciones e^{2 πip · x⁄h}. Estas son soluciones de onda plana de la ecuación de Schrödinger para una partícula libre, pero no son normalizables, por lo tanto, no en L². Pero son, no obstante, fundamentales para la descripción. Uno puede, usándolos, expresar funciones que son normalizables usando paquetes de ondas. Son, en cierto sentido, una base (pero no una base espacial de Hilbert, ni una base de Hamel) en la que se pueden expresar las funciones de onda de interés. También existe el artefacto "normalización a una función delta" que se emplea con frecuencia por conveniencia de notación, ver más abajo. Las funciones delta en sí mismas tampoco son integrables al cuadrado.

La descripción anterior del espacio funcional que contiene las funciones de onda tiene una motivación principalmente matemática. Los espacios funcionales son, debido a su completitud, muy grandes en cierto sentido. No todas las funciones son descripciones realistas de cualquier sistema físico. Por ejemplo, en el espacio de funciones L² se puede encontrar la función que toma el valor 0 para todos los números racionales y -i para los irracionales en el intervalo [0, 1]. Este es integrable al cuadrado, pero difícilmente puede representar un estado físico.

Espacios comunes de Hilbert

Si bien el espacio de soluciones como un todo es un espacio de Hilbert, hay muchos otros espacios de Hilbert que comúnmente ocurren como ingredientes.

• Funciones complejas integradas cuadradas valoradas en el intervalo [0, 2π]. El set {}e^int/2π, n. es una base espacial Hilbert, es decir, un conjunto ortonormal maximal.
• La transformación Fourier tiene funciones en el espacio anterior a elementos de l²(Z), el espacio de cuadrada funciones Z → C. Este último espacio es un espacio Hilbert y la transformación Fourier es un isomorfismo de los espacios de Hilbert. Su base es {}e_i, i. con e_i()j) δ_ij, i, j ▪ Z.
• El ejemplo más básico de polinomios abarcadores está en el espacio de funciones integradas cuadradas en el intervalo [–1, 1] para los polinomios Legendre es una base espacial Hilbert (completo conjunto ortonormal).
• Funciones integradas cuadradas en la esfera de unidad S² es un espacio de Hilbert. Las funciones de base en este caso son las armónicas esféricas. Los polinomios Legendre son ingredientes en la armónica esférica. La mayoría de los problemas con la simetría rotacional tendrán "la misma" (conocida) solución con respecto a esa simetría, por lo que el problema original se reduce a un problema de menor dimensionalidad.
• Los polinomios Laguerre asociados aparecen en el problema de la función de onda hidrógeno después de tener en cuenta las armónicas esféricas. Estos abarcan el espacio Hilbert de funciones integradas cuadradas en el intervalo semiinfinito [0, ∞].

De manera más general, se puede considerar un tratamiento unificado de todas las soluciones polinómicas de segundo orden para las ecuaciones de Sturm-Liouville en el entorno del espacio de Hilbert. Estos incluyen los polinomios de Legendre y Laguerre, así como los polinomios de Chebyshev, los polinomios de Jacobi y los polinomios de Hermite. Todos estos aparecen realmente en problemas físicos, los últimos en el oscilador armónico, y lo que de otro modo es un desconcertante laberinto de propiedades de funciones especiales se convierte en un cuerpo organizado de hechos. Para esto, véase Byron & Fuller (1992, capítulo 5).

Existen también espacios de Hilbert de dimensión finita. El espacio ℂⁿ es un espacio de Hilbert de dimensión n. El producto interior es el producto interior estándar en estos espacios. En él, la "parte giratoria" reside la función de onda de una sola partícula.

• En la descripción no relativista de un electron uno tiene n = 2 y la función total de onda es una solución de la ecuación Pauli.
• En el tratamiento relativista correspondiente, n = 4 y la función de onda resuelve la ecuación Dirac.

Con más partículas, la situación es más complicada. Uno tiene que emplear productos tensoriales y usar la teoría de representación de los grupos de simetría involucrados (el grupo de rotación y el grupo de Lorentz respectivamente) para extraer del producto tensorial los espacios en los que residen las funciones de onda de espín (totales). (Surgen más problemas en el caso relativista a menos que las partículas estén libres. Consulte la ecuación de Bethe-Salpeter). Las observaciones correspondientes se aplican al concepto de isospin, para el cual el grupo de simetría es SU (2). Los modelos de las fuerzas nucleares de los años sesenta (todavía útiles hoy en día, ver fuerza nuclear) usaban el grupo de simetría SU(3). En este caso, también, la parte de las funciones de onda correspondientes a las simetrías internas residen en algunos ℂⁿ o subespacios de productos tensoriales de tales espacios.

• En la teoría de campo cuántica, el espacio subyacente de Hilbert es el espacio Fock. Se construye a partir de estados libres de partículas individuales, es decir, funciones de onda cuando se elige una representación, y puede acomodar cualquier finito, no necesariamente constante en el tiempo, número de partículas. El interesante (o más bien el tratable) dinámica no se encuentra en las funciones de onda sino en los operadores de campo que son operadores que actúan en el espacio Fock. Así el cuadro Heisenberg es la opción más común (estados constantes, operadores de tiempo variable).

Debido a la naturaleza de dimensión infinita del sistema, las herramientas matemáticas apropiadas son objeto de estudio en el análisis funcional.

Descripción simplificada

Continuidad de la función de onda y su primer derivado espacial (en la x dirección, Sí. y z coordenadas no mostradas), en algún momento t.

No todos los libros de texto introductorios toman el camino largo e introducen la maquinaria espacial completa de Hilbert, pero el enfoque está en la ecuación de Schrödinger no relativista en representación de posición para ciertos potenciales estándar. Las siguientes restricciones sobre la función de onda a veces se formulan explícitamente para que los cálculos y la interpretación física tengan sentido:

• La función de onda debe ser integrada cuadrada. Esto está motivado por la interpretación de Copenhague de la función de onda como una amplitud de probabilidad.
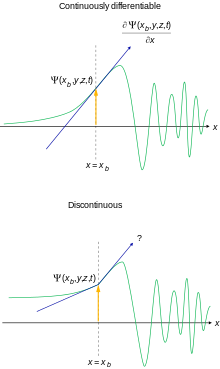
• Debe ser en todas partes continuo y en todas partes continuamente diferente. Esto está motivado por la aparición de la ecuación Schrödinger para la mayoría de los potenciales físicamente razonables.

Es posible relajar un poco estas condiciones para propósitos especiales. Si no se cumplen estos requisitos, no es posible interpretar la función de onda como una amplitud de probabilidad.

Esto no altera la estructura del espacio de Hilbert en el que habitan estas funciones de onda particulares, sino el subespacio de las funciones integrables al cuadrado L², que es un espacio de Hilbert, que satisface el segundo requisito no está cerrado en L², por lo tanto, no es un espacio de Hilbert en sí mismo. Las funciones que no cumplen con los requisitos siguen siendo necesarias por razones técnicas y prácticas.

Más sobre funciones de onda y espacio de estado abstracto

Como se ha demostrado, el conjunto de todas las funciones de onda posibles en alguna representación para un sistema constituyen un espacio de Hilbert de dimensión infinita en general. Debido a las múltiples opciones posibles de base de representación, estos espacios de Hilbert no son únicos. Por lo tanto, se habla de un espacio de Hilbert abstracto, espacio de estado, donde la elección de representación y base queda indeterminada. Específicamente, cada estado se representa como un vector abstracto en el espacio de estados. Un estado cuántico |Ψ⟩ en cualquier representación generalmente se expresa como un vector

SilencioΨ Ψ .. =.. α α ∫ ∫ dm⋅ ⋅ Ψ Ψ ()α α ,⋅ ⋅ ,t)Silencioα α ,⋅ ⋅ .. {displaystyle SilencioPsi rangle =sum _{boldsymbol {alpha }int d^{m}!{boldsymbol {omega },,Psi ({boldsymbol {alpha }},{boldsymbol {omega }},t), sometida{boldsymbol {alpha }},{boldsymbol {omega }rangle }

• Silencioα, ⋅. los vectores base de la representación elegida
• d^m⋅ = dω₁dω₂...dω_m un "elemento de volumen diferente" en los grados continuos de libertad
• Ψα, ⋅, t) un componente del vector ←, llamado el función de onda del sistema
• α =α₁, α₂,... α_n) números cuánticos discretos
• ⋅ =⋅₁, ⋅₂,... ⋅_m) variables continuas (no necesariamente sin dimensión)

Estos números cuánticos indexan los componentes del vector de estado. Más aún, todos los α están en un conjunto n-dimensional A = A₁ × A₂ ×... × A_n donde cada A_i es el conjunto de valores permitidos para α_i; todos los ω están en una m-dimensional " volumen" Ω ⊆ ℝ^m donde Ω = Ω₁ × Ω₂ ×... × Ω_m y cada Ω_i ⊆ R es el conjunto de valores permitidos para ω_i, un subconjunto de los números reales R. Para generalidad n y m no son necesariamente iguales.

Ejemplo:

La densidad de probabilidad de encontrar el sistema a tiempo t{displaystyle t}en estado Silencioα, ⋅. es

*** *** α α ,⋅ ⋅ ()t)=SilencioΨ Ψ ()α α ,⋅ ⋅ ,t)Silencio2{displaystyle rho _{alphaomega }(t)= foreverPsi ({boldsymbol {alpha }},{boldsymbol {omega },t)

La probabilidad de encontrar un sistema con α en algunas o todas las posibles configuraciones de variables discretas, D ⊆ A, y ω en algunas o todas las posibles configuraciones de variable continua, C ⊆ Ω, es la suma y la integral sobre la densidad,

P()t)=.. α α ▪ ▪ D∫ ∫ C*** *** α α ,⋅ ⋅ ()t)dm⋅ ⋅ {displaystyle P(t)=sum _{boldsymbol {Alpha}in D'in _{C}rho _{alphaomega }(t),,d^{m}!{boldsymbol {omega }}

Dado que la suma de todas las probabilidades debe ser 1, la condición de normalización

1=.. α α ▪ ▪ A∫ ∫ Ω Ω *** *** α α ,⋅ ⋅ ()t)dm⋅ ⋅ {displaystyle 1=sum _{boldsymbol {Alpha }in A}int _{Omega }rho _{alphaomega }(t),d^{m}!{boldsymbol {omega }}

La condición de normalización requiere que ρ d^mω sea adimensional, por dimensión el análisis Ψ debe tener las mismas unidades que (ω₁ω₂...ω_m)^−1/2.

Ontología

Si la función de onda realmente existe y qué representa, son preguntas importantes en la interpretación de la mecánica cuántica. Muchos físicos famosos de una generación anterior se quedaron perplejos ante este problema, como Schrödinger, Einstein y Bohr. Algunos abogan por formulaciones o variantes de la interpretación de Copenhague (p. ej., Bohr, Wigner y von Neumann), mientras que otros, como Wheeler o Jaynes, adoptan el enfoque más clásico y consideran que la función de onda representa información en la mente del observador, es decir, una medida de nuestro conocimiento de la realidad. Algunos, incluidos Schrödinger, Bohm y Everett y otros, argumentaron que la función de onda debe tener una existencia física objetiva. Einstein pensó que una descripción completa de la realidad física debería referirse directamente al espacio y al tiempo físicos, a diferencia de la función de onda, que se refiere a un espacio matemático abstracto.

Observaciones

Fuentes generales