Función de error

ImprimirCitar

Función especial de forma sigmoide

En matemáticas, la función de error (también llamada función de error de Gauss), a menudo denotada por $erf$ , es una función compleja de una variable compleja definida como:

{displaystyle operatorname {erf} z={frac {2}{sqrt {pi }}}int _{0}^{z}e^{-t^{2}},mathrm {d} t.}

Algunos autores definen $operatorname {erf}$ sin el factor de ${displaystyle 2/{sqrt {pi }}}$ . Esta integral es una función sigmoide especial (no elemental) que ocurre a menudo en probabilidad, estadísticas y ecuaciones diferenciales parciales. En muchas de estas aplicaciones, el argumento de la función es un número real. Si el argumento de la función es real, entonces el valor de la función también es real.

En estadística, para valores no negativos de $x$ , la función de error tiene la siguiente interpretación: para una variable aleatoria $Y$ que se distribuye normalmente con media 0 y desviación estándar $1 / \sqrt 2$ , $erf x$ es la probabilidad de que $Y$ caiga en el rango $[- x, x]$ .

Dos funciones estrechamente relacionadas son la función de error complementaria ( $erfc$ ) definida como

{displaystyle operatorname {erfc} z=1-operatorname {erf} z,}

y la función de error imaginario ( $erfi$ ) definida como

{displaystyle operatorname {erfi} z=-ioperatorname {erf} iz,}

donde $i$ es la unidad imaginaria.

Nombre

El nombre "función de error" y su abreviatura $erf$ fueron propuestos por J. W. L. Glaisher en 1871 debido a su conexión con "la teoría de la probabilidad, y en particular la teoría de los errores." El complemento de la función de error también fue discutido por Glaisher en una publicación separada en el mismo año. Por la "ley de facilidad" de errores cuya densidad viene dada por

{displaystyle f(x)=left({frac {c}{pi }}right)^{frac {1}{2}}e^{-cx^{2}}}

(la distribución normal), Glaisher calcula la probabilidad de un error entre $p$ y $q$ como:

{displaystyle left({frac {c}{pi }}right)^{frac {1}{2}}int _{p}^{q}e^{-cx^{2}},mathrm {d} x={tfrac {1}{2}}left(operatorname {erf} left(q{sqrt {c}}right)-operatorname {erf} left(p{sqrt {c}}right)right).}

Parcela de la función de error Erf(z) en el plano complejo de -2-2i a 2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D

Aplicaciones

Cuando los resultados de una serie de mediciones se describen mediante una distribución normal con desviación estándar $σ$ y valor esperado 0, entonces $erf (a / σ \sqrt 2)$ es la probabilidad de que el error de una sola medición se encuentre entre $- a$ y $+ a$ , para positivo $a$ . Esto es útil, por ejemplo, para determinar la tasa de error de bit de un sistema de comunicación digital.

Las funciones de error y de error complementarias ocurren, por ejemplo, en soluciones de la ecuación del calor cuando las condiciones de contorno están dadas por la función escalón de Heaviside.

La función de error y sus aproximaciones se pueden usar para estimar resultados que se cumplen con alta o baja probabilidad. Dada una variable aleatoria $X ~ Norm[μ, σ]$ (una distribución normal con media $μ$ y desviación estándar $σ$ ) y una constante $L < μ$ :

{displaystyle {begin{aligned}Pr[Xleq L]&={frac {1}{2}}+{frac {1}{2}}operatorname {erf} {frac {L-mu }{{sqrt {2}}sigma }}\&approx Aexp left(-Bleft({frac {L-mu }{sigma }}right)^{2}right)end{aligned}}}

donde $A$ y $B$ son ciertas constantes numéricas. Si $L$ está lo suficientemente lejos de la media, específicamente $μ - L \geq σ \sqrt ln k$ , entonces:

{displaystyle Pr[Xleq L]leq Aexp(-Bln {k})={frac {A}{k^{B}}}}

entonces la probabilidad llega a 0 cuando $k \to \infty$ .

La probabilidad de que $X$ esté en el intervalo $[L a, L b]$ se puede derivar como

{displaystyle {begin{aligned}Pr[L_{a}leq Xleq L_{b}]&=int _{L_{a}}^{L_{b}}{frac {1}{{sqrt {2pi }}sigma }}exp left(-{frac {(x-mu)^{2}}{2sigma ^{2}}}right),mathrm {d} x\&={frac {1}{2}}left(operatorname {erf} {frac {L_{b}-mu }{{sqrt {2}}sigma }}-operatorname {erf} {frac {L_{a}-mu }{{sqrt {2}}sigma }}right).end{aligned}}}

Propiedades

Parcelas en el plano complejo

Integrand

exp(z 2)

er z

La propiedad $erf (- z) = -erf z$ significa que la función de error es una función impar. Esto resulta directamente del hecho de que el integrando $e - t 2$ es una función par (la antiderivada de una función par que es cero en el origen es una función impar y viceversa).

Dado que la función de error es una función completa que convierte números reales en números reales, para cualquier número complejo $z$ :

{displaystyle operatorname {erf} {overline {z}}={overline {operatorname {erf} z}}}

donde $z$ es el conjugado complejo de z .

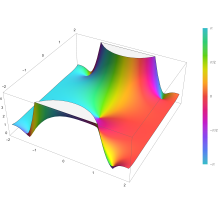
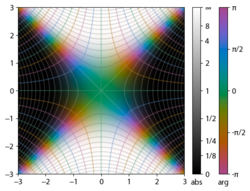
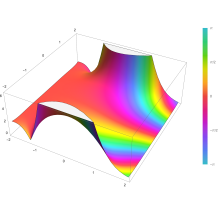
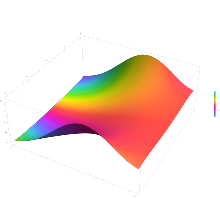
El integrando $f = exp(- z 2)$ y $f = erf z$ se muestran en el complejo $z$ en las figuras de la derecha con coloración de dominio.

La función de error en $+\infty$ es exactamente 1 (ver integral de Gauss). En el eje real, $erf z$ se aproxima a la unidad en $z \to +\infty$ y −1 en $z \to -\infty$ . En el eje imaginario, tiende a $\pm i \infty$ .

Serie Taylor

La función de error es una función completa; no tiene singularidades (excepto en el infinito) y su desarrollo de Taylor siempre converge, pero es famoso "[...] por su mala convergencia si $x > 1$ ."

La integral definitoria no puede evaluarse en forma cerrada en términos de funciones elementales, sino expandiendo el integrando $e - z 2$ en su serie de Maclaurin e integrando término a término, se obtiene la serie de Maclaurin de la función de error como:

{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z-{frac {z^{3}}{3}}+{frac {z^{5}}{10}}-{frac {z^{7}}{42}}+{frac {z^{9}}{216}}-cdots right)end{aligned}}}

que se cumple para cada número complejo $z$ . Los términos del denominador son la secuencia A007680 en el OEIS.

Para el cálculo iterativo de la serie anterior, la siguiente formulación alternativa puede ser útil:

{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }left(zprod _{k=1}^{n}{frac {-(2k-1)z^{2}}{k(2k+1)}}right)\[6pt]&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z}{2n+1}}prod _{k=1}^{n}{frac {-z^{2}}{k}}end{aligned}}}

porque $-(2 k - 1) z 2 / k (2 k + 1)$ expresa el multiplicador para convertir el $k$ th término en el $(k + 1)$ th término (considerando $z$ como primer término).

La función de error imaginario tiene una serie de Maclaurin muy similar, que es:

{displaystyle {begin{aligned}operatorname {erfi} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z+{frac {z^{3}}{3}}+{frac {z^{5}}{10}}+{frac {z^{7}}{42}}+{frac {z^{9}}{216}}+cdots right)end{aligned}}}

que se cumple para cada número complejo $z$ .

Derivada e integral

La derivada de la función de error se sigue inmediatamente de su definición:

{displaystyle {frac {mathrm {d} }{mathrm {d} z}}operatorname {erf} z={frac {2}{sqrt {pi }}}e^{-z^{2}}.}

A partir de esto, la derivada de la función de error imaginario también es inmediata:

{displaystyle {frac {d}{dz}}operatorname {erfi} z={frac {2}{sqrt {pi }}}e^{z^{2}}.}

Una antiderivada de la función de error, obtenible por integración por partes, es

{displaystyle zoperatorname {erf} z+{frac {e^{-z^{2}}}{sqrt {pi }}}.}

Una antiderivada de la función de error imaginario, también obtenible por integración por partes, es

{displaystyle zoperatorname {erfi} z-{frac {e^{z^{2}}}{sqrt {pi }}}.}

Las derivadas de orden superior están dadas por

{displaystyle operatorname {erf} ^{(k)}z={frac {2(-1)^{k-1}}{sqrt {pi }}}{mathit {H}}_{k-1}(z)e^{-z^{2}}={frac {2}{sqrt {pi }}}{frac {mathrm {d} ^{k-1}}{mathrm {d} z^{k-1}}}left(e^{-z^{2}}right),qquad k=1,2,dots }

donde $H$ son los físicos' Polinomios de Hermite.

Serie Bürmann

Usando Hans Heinrich se obtiene una expansión, que converge más rápidamente para todos los valores reales de $x$ que una expansión de Taylor. Teorema de Bürmann:

{displaystyle {begin{aligned}operatorname {erf} x&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left(1-{frac {1}{12}}left(1-e^{-x^{2}}right)-{frac {7}{480}}left(1-e^{-x^{2}}right)^{2}-{frac {5}{896}}left(1-e^{-x^{2}}right)^{3}-{frac {787}{276480}}left(1-e^{-x^{2}}right)^{4}-cdots right)\[10pt]&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left({frac {sqrt {pi }}{2}}+sum _{k=1}^{infty }c_{k}e^{-kx^{2}}right).end{aligned}}}

donde $sgn$ es la función de signo. Manteniendo solo los dos primeros coeficientes y eligiendo $c 1 = 31 / 200$ y $c 2 = - 341 / 8000$ , la aproximación resultante muestra su mayor error relativo en $x = \pm1,3796$ , donde es menor que 0,0036127:

{displaystyle operatorname {erf} xapprox {frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left({frac {sqrt {pi }}{2}}+{frac {31}{200}}e^{-x^{2}}-{frac {341}{8000}}e^{-2x^{2}}right).}

Funciones inversas

Función de error inversa

Dado un número complejo $z$ , no existe un número complejo único $w$ satisfaciendo $erf w = z$ , por lo que una función inversa verdadera sería multivaluada. Sin embargo, para $-1 < x < 1$ , hay un número real único denominado $erf -1 x$ satisfactorio

{displaystyle operatorname {erf} left(operatorname {erf} ^{-1}xright)=x.}

La función de error inverso generalmente se define con el dominio $(-1,1)$ , y está restringida a este dominio en muchos sistemas de álgebra computacional. Sin embargo, se puede extender al disco $| z | < 1$ del plano complejo, utilizando la serie de Maclaurin

{displaystyle operatorname {erf} ^{-1}z=sum _{k=0}^{infty }{frac {c_{k}}{2k+1}}left({frac {sqrt {pi }}{2}}zright)^{2k+1},}

donde $c 0 = 1$ y

{displaystyle {begin{aligned}c_{k}&=sum _{m=0}^{k-1}{frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}\&=left{1,1,{frac {7}{6}},{frac {127}{90}},{frac {4369}{2520}},{frac {34807}{16200}},ldots right}.end{aligned}}}

Así que tenemos la expansión en serie (los factores comunes se han cancelado de numeradores y denominadores):

{displaystyle operatorname {erf} ^{-1}z={frac {sqrt {pi }}{2}}left(z+{frac {pi }{12}}z^{3}+{frac {7pi ^{2}}{480}}z^{5}+{frac {127pi ^{3}}{40320}}z^{7}+{frac {4369pi ^{4}}{5806080}}z^{9}+{frac {34807pi ^{5}}{182476800}}z^{11}+cdots right).}

(Después de la cancelación, las fracciones del numerador/denominador son entradas OEIS: A092676/OEIS: A092677 en el OEIS; sin cancelación, los términos del numerador se dan en la entrada OEIS: A002067). El valor de la función de error en $\pm\infty$ es igual a $\pm1$ .

Para $| z | < 1$ , tenemos $erf(erf -1 z) = z$ .

La función inversa de error complementario se define como

{displaystyle operatorname {erfc} ^{-1}(1-z)=operatorname {erf} ^{-1}z.}

Para $x$ reales, hay un número real único $erfi -1 x$ satisfaciendo $erfi(erfi -1 x) = x$ . La función de error imaginario inverso se define como $erfi -1 x$ .

Para cualquier x real, el método de Newton se puede usar para calcular $erfi -1 x$ , y para $-1 \leq x \leq 1$ , la siguiente serie de Maclaurin converge:

{displaystyle operatorname {erfi} ^{-1}z=sum _{k=0}^{infty }{frac {(-1)^{k}c_{k}}{2k+1}}left({frac {sqrt {pi }}{2}}zright)^{2k+1},}

donde $c k$ se define como arriba.

Expansión asintótica

Una expansión asintótica útil de la función de error complementaria (y por lo tanto también de la función de error) para grandes $x$ reales es

{displaystyle {begin{aligned}operatorname {erfc} x&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}left(1+sum _{n=1}^{infty }(-1)^{n}{frac {1cdot 3cdot 5cdots (2n-1)}{left(2x^{2}right)^{n}}}right)\[6pt]&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}sum _{n=0}^{infty }(-1)^{n}{frac {(2n-1)!!}{left(2x^{2}right)^{n}}},end{aligned}}}

donde $(2 n - 1)!!$ es el factorial doble de $(2 n - 1)$ , que es el producto de todos los números impares hasta $(2 n - 1)$ . Esta serie diverge para todo finito $x$ , y su significado como expansión asintótica es que para cualquier entero $N \geq 1$ uno tiene

{displaystyle operatorname {erfc} x={frac {e^{-x^{2}}}{x{sqrt {pi }}}}sum _{n=0}^{N-1}(-1)^{n}{frac {(2n-1)!!}{left(2x^{2}right)^{n}}}+R_{N}(x)}

donde el resto, en notación de Landau, es

{displaystyle R_{N}(x)=Oleft(x^{-(1+2N)}e^{-x^{2}}right)}

como $x \to \infty$ .

De hecho, el valor exacto del resto es

{displaystyle R_{N}(x):={frac {(-1)^{N}}{sqrt {pi }}}2^{1-2N}{frac {(2N)!}{N!}}int _{x}^{infty }t^{-2N}e^{-t^{2}},mathrm {d} t,}

que sigue fácilmente por inducción, escribiendo

{displaystyle e^{-t^{2}}=-(2t)^{-1}left(e^{-t^{2}}right)'}

e integrando por partes.

Para valores suficientemente grandes de $x$ , solo se necesitan los primeros términos de esta expansión asintótica para obtener una buena aproximación de $erfc x$ (mientras que para valores no demasiado grandes de $x$ , la expansión de Taylor anterior en 0 proporciona una convergencia muy rápida).

Expansión continua de fracciones

Una expansión en fracción continua de la función de error complementaria es:

{displaystyle operatorname {erfc} z={frac {z}{sqrt {pi }}}e^{-z^{2}}{cfrac {1}{z^{2}+{cfrac {a_{1}}{1+{cfrac {a_{2}}{z^{2}+{cfrac {a_{3}}{1+dotsb }}}}}}}},qquad a_{m}={frac {m}{2}}.}

Integral de función de error con función de densidad gaussiana

{displaystyle int _{-infty }^{infty }operatorname {erf} left(ax+bright){frac {1}{sqrt {2pi sigma ^{2}}}}exp left(-{frac {(x-mu)^{2}}{2sigma ^{2}}}right),mathrm {d} x=operatorname {erf} {frac {amu +b}{sqrt {1+2a^{2}sigma ^{2}}}},qquad a,b,musigma in mathbb {R} }

que aparece relacionado con Ng y Geller, fórmula 13 en la sección 4.3 con un cambio de variables.

Serie factorial

La serie factorial inversa:

{displaystyle {begin{aligned}operatorname {erfc} z&={frac {e^{-z^{2}}}{{sqrt {pi }},z}}sum _{n=0}^{infty }{frac {(-1)^{n}Q_{n}}{{(z^{2}+1)}^{bar {n}}}}\&={frac {e^{-z^{2}}}{{sqrt {pi }},z}}left(1-{frac {1}{2}}{frac {1}{(z^{2}+1)}}+{frac {1}{4}}{frac {1}{(z^{2}+1)(z^{2}+2)}}-cdots right)end{aligned}}}

converge para $Re(z 2) > 0$ . Aquí

{displaystyle {begin{aligned}Q_{n}&{overset {text{def}}{{}={}}}{frac {1}{Gamma left({frac {1}{2}}right)}}int _{0}^{infty }tau (tau -1)cdots (tau -n+1)tau ^{-{frac {1}{2}}}e^{-tau },dtau \&=sum _{k=0}^{n}left({tfrac {1}{2}}right)^{bar {k}}s(n,k),end{aligned}}}

$z n$ denota el factorial ascendente y $s (n, k)$ denota un número de Stirling con signo del primer tipo. También existe una representación por una suma infinita que contiene el doble factorial:

{displaystyle operatorname {erf} z={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {(-2)^{n}(2n-1)!!}{(2n+1)!}}z^{2n+1}}

Aproximaciones numéricas

Aproximación con funciones elementales

Abramowitz y Stegun ofrecen varias aproximaciones de precisión variable (ecuaciones 7.1.25–28). Esto permite elegir la aproximación más rápida adecuada para una aplicación dada. Para aumentar la precisión, son:
${displaystyle operatorname {erf} xapprox 1-{frac {1}{left(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}right)^{4}}},qquad xgeq 0}$
(Máximo error: 5×10⁻⁴)
Donde $a 1 = 0,278393$ , $a 2 = 0,30389$ , $a 3 = 0,000972$ , $a 4 = 0,078108$
${displaystyle operatorname {erf} xapprox 1-left(a_{1}t+a_{2}t^{2}+a_{3}t^{3}right)e^{-x^{2}},quad t={frac {1}{1+px}},qquad xgeq 0}$
(Máximo error: 2.5×10^{; 5 -})
Donde $p = 0,47047$ , $a 1 = 0,3480242$ , $a 2 = 0,0958798$ , $a 3 = 0,478556$
${displaystyle operatorname {erf} xapprox 1-{frac {1}{left(1+a_{1}x+a_{2}x^{2}+cdots +a_{6}x^{6}right)^{16}}},qquad xgeq 0}$ (Máximo error: 3×10⁻⁷)
Donde $a 1 = 0,0705230784$ , $a 2 = 0,0422820123$ , $a 3 = 0,0092705272$ , $a 4 = 0,0001520143$ , $a 5 = 0,0002765672$ , $a 6 = 0,0000430638$
${displaystyle operatorname {erf} xapprox 1-left(a_{1}t+a_{2}t^{2}+cdots +a_{5}t^{5}right)e^{-x^{2}},quad t={frac {1}{1+px}}}$ (Máximo error: 1,5×10⁻⁷)
Donde $p = 0,275911$ , $a 1 = 0,254829592$ , $a 2 = 0,284496736$ , $a 3 = 1.421413741$ , $a 4 = 1,453152027$ , $a 5 = 1.061405429$
Todas estas aproximaciones son válidas para $x \geq 0$ . Para utilizar estas aproximaciones para negativo $x$ , utilizar el hecho de que $er x$ es una función extraña, así que $er x = -erf x)$ .
Los límites exponenciales y una aproximación exponencial pura para la función de error complementario son dadas por
$0\operatorname {erfc} x&approx {tfrac {1}{6}}e^{-x^{2}}+{tfrac {1}{2}}e^{-{frac {4}{3}}x^{2}},&quad x&>0.end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">erfc⁡ ⁡ x≤ ≤ 12e− − 2x2+12e− − x2≤ ≤ e− − x2,x■0erfc⁡ ⁡ x.. 16e− − x2+12e− − 43x2,x■0.{displaystyle {begin{aligned}operatorname {erfc} x pacienteleq {tfrac} {1}{2}e^{-2x^{2}}+{tfrac {1} {2}e^{-x^{2}}leq e^{-x^{2}}, ################################################################################################################################################################################################################################################################ {erfc} x pacienteapprox {tfrac} {1} {6}e^{-x^{2}+{tfrac} {1}{2}e^{-{frac {4} {3}x^{2}}, âquad x consigo0.end{aligned}}0\operatorname {erfc} x&approx {tfrac {1}{6}}e^{-x^{2}}+{tfrac {1}{2}}e^{-{frac {4}{3}}x^{2}},&quad x&>0.end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cf4a1576135546bf49c0f2eb85e8165275aa8d02" style="vertical-align: -3.465ex; margin-bottom: -0.206ex; width:46.282ex; height:8.509ex;"/>$
Lo anterior se ha generalizado a sumas de $N$ exponenciales con mayor precisión en términos de $N$ así $erfc x$ puede ser exactamente aproximado o atado por $2 Q ? () \sqrt 2 x)$ , donde
${displaystyle {tilde {Q}}(x)=sum _{n=1}^{N}a_{n}e^{-b_{n}x^{2}}.}$
En particular, existe una metodología sistemática para resolver los coeficientes numéricos $[a n, b n) N n = 1$ que produce una aproximación minimax o ligada a la función Q estrechamente relacionada: $Q () x) Q ? () x)$ , $Q () x \leq Q ? () x)$ , o $Q () x) \geq Q ? () x)$ para $x \geq 0$ . Los coeficientes $[a n, b n) N n = 1$ para muchas variaciones de las aproximaciones y límites exponenciales hasta $N = 25$ han sido liberados para abrir el acceso como conjunto de datos completo.
Una aproximación estrecha de la función de error complementario para $x (0, mujeres)$ es dado por Karagiannidis " Lioumpas (2007) que mostró la elección adecuada de parámetros ${} A, B}$ que
${displaystyle operatorname {erfc} xapprox {frac {left(1-e^{-Ax}right)e^{-x^{2}}}{B{sqrt {pi }}x}}.}$
Ellos determinaron ${} A, B} = {1.98,1.135}$ , que dio una buena aproximación para todos $x \geq 0$ . También están disponibles coeficientes alternativos para la precisión de la adaptación para una aplicación específica o la transformación de la expresión en un límite ajustado.
Un límite inferior de un solo plazo es
$1,}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">erfc⁡ ⁡ x≥ ≥ 2eπ π β β − − 1β β e− − β β x2,x≥ ≥ 0,β β ■1,{displaystyle operatorname {erfc} xgeq {sqrt {frac {2e}{pi} {beta}} {beta {beta} {beta}}e^{-beta x^{2}}}qquad xgeq 0,quad beta #1,}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ca3a4cad21677fa011b495f5665235d20d8bb0af" style="vertical-align: -2.338ex; width:48.578ex; height:6.676ex;"/>$
donde el parámetro $β$ se puede elegir para minimizar el error en el intervalo deseado de aproximación.
Otra aproximación es dada por Sergei Winitzki usando sus "aproximaciones de Padé global":
${displaystyle operatorname {erf} xapprox operatorname {sgn} xcdot {sqrt {1-exp left(-x^{2}{frac {{frac {4}{pi }}+ax^{2}}{1+ax^{2}}}right)}}}$
Donde
${displaystyle a={frac {8(pi -3)}{3pi (4-pi)}}approx 0.140012.}$
Esto está diseñado para ser muy preciso en un barrio de 0 y un barrio de infinito, y el relativo error es menos de 0.00035 para todo real $x$ . Utilizando el valor alternativo $a Entendido 0.147$ reduce el error relativo máximo a alrededor de 0.00013.
Esta aproximación se puede invertir para obtener una aproximación para la función de error inverso:
${displaystyle operatorname {erf} ^{-1}xapprox operatorname {sgn} xcdot {sqrt {{sqrt {left({frac {2}{pi a}}+{frac {ln left(1-x^{2}right)}{2}}right)^{2}-{frac {ln left(1-x^{2}right)}{a}}}}-left({frac {2}{pi a}}+{frac {ln left(1-x^{2}right)}{2}}right)}}.}$
Una aproximación con un error máximo de 1.2×10⁻⁷ para cualquier argumento real es:
$<math alttext="{displaystyle operatorname {erf} x={begin{cases}1-tau &xgeq 0\tau -1&xer⁡ ⁡ x={}1− − τ τ x≥ ≥ 0τ τ − − 1x.0{displaystyle operatorname {erf} x={begin{cases}1-tau &xgeq 0\\\\tau -1 limite 0end{cases}}<img alt="{displaystyle operatorname {erf} x={begin{cases}1-tau &xgeq 0\tau -1&x$
con
${displaystyle {begin{aligned}tau &=tcdot exp left(-x^{2}-1.26551223+1.00002368t+0.37409196t^{2}+0.09678418t^{3}-0.18628806t^{4}right.\&left.qquad qquad qquad +0.27886807t^{5}-1.13520398t^{6}+1.48851587t^{7}-0.82215223t^{8}+0.17087277t^{9}right)end{aligned}}}$
y
${displaystyle t={frac {1}{1+{frac {1}{2}}|x|}}.}$

Tabla de valores

$x$	$er x$	$1 - erf x$
0	0	1
0,02	0,022564575	0.977435425
0,04	0,045111106	0.954888894
0,06	0,067621594	0.932378406
0,08	0,090078126	0.909921874
0.1	0.112462916	0.887537084
0.2	0.222702589	0,777297411
0.3	0,328626759	0.671373241
0,4	0.428392355	0.571607645
0.5	0,520499878	0.479500122
0.6	0,603856091	0,396143909
0.7	0.677801194	0.322198806
0,8	0,722100965	0,257899035
0.9	0,769908212	0.203091788
1	0.842700793	0.157299207
1.1	0.880205070	0.119794930
1.2	0.910313978	0,089686022
1.3	0.934007945	0,065992055
1.4	0.952285120	0,047714880
1,5	0.966105146	0,033894854
1.6	0.976348383	0,023651617
1.7	0.983790459	0,016209541
1.8	0.989090502	0,010909498
1.9	0.992790429	0,007209571
2	0.995322265	0,004677735
2.1	0.997020533	0,002979467
2.2	0.998137154	0,001862846
2.3	0.998856823	0,001143177
2.4	0.999311486	0,000688514
2.5	0.999593048	0,000406952
3	0.999977910	0,000022090
3.5	0.999999257	0,000000743

Funciones relacionadas

Función de error complementaria

La función de error complementaria, denominada $erfc$ , se define como

Parcela de la función de error complementaria Erfc(z) en el plano complejo de -2-2i a 2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D

{displaystyle {begin{aligned}operatorname {erfc} x&=1-operatorname {erf} x\[5pt]&={frac {2}{sqrt {pi }}}int _{x}^{infty }e^{-t^{2}},mathrm {d} t\[5pt]&=e^{-x^{2}}operatorname {erfcx} x,end{aligned}}}

que también define $erfcx$ , la función de error complementaria escalada (que se puede usar en lugar de $erfc$ para evitar el subdesbordamiento aritmético). Otra forma de $erfc x$ para $x \geq 0$ se conoce como La fórmula de Craig, según su descubridor:

{displaystyle operatorname {erfc} (xmid xgeq 0)={frac {2}{pi }}int _{0}^{frac {pi }{2}}exp left(-{frac {x^{2}}{sin ^{2}theta }}right),mathrm {d} theta.}

Esta expresión solo es válida para valores positivos de $x$ , pero se puede usar junto con $erfc x = 2 - erfc(- x)$ para obtener $erfc(x)$ para valores negativos. Esta forma es ventajosa porque el rango de integración es fijo y finito. Una extensión de esta expresión para el $erfc$ de la suma de dos variables no negativas es la siguiente:

{displaystyle operatorname {erfc} (x+ymid x,ygeq 0)={frac {2}{pi }}int _{0}^{frac {pi }{2}}exp left(-{frac {x^{2}}{sin ^{2}theta }}-{frac {y^{2}}{cos ^{2}theta }}right),mathrm {d} theta.}

Función de error imaginario

La función de error imaginario, denominada $erfi$ , se define como

Parcela de la función de error imaginario Erfi(z) en el plano complejo de -2-2i a 2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D

{displaystyle {begin{aligned}operatorname {erfi} x&=-ioperatorname {erf} ix\[5pt]&={frac {2}{sqrt {pi }}}int _{0}^{x}e^{t^{2}},mathrm {d} t\[5pt]&={frac {2}{sqrt {pi }}}e^{x^{2}}D(x),end{aligned}}}

donde $D (x)$ es la función de Dawson (que se puede usar en lugar de $erfi$ para evitar el desbordamiento aritmético).

A pesar del nombre "función de error imaginario", $erfi x$ es real cuando el estilo $x$ es real.

Cuando la función de error se evalúa para argumentos complejos arbitrarios $z$ , la función de error complejo resultante generalmente se analiza en forma escalada como la función de Faddeeva:

w(z)=e^{-z^{2}}operatorname {erfc} (-iz)=operatorname {erfcx} (-iz).

Función de distribución acumulativa

La función de error es esencialmente idéntica a la función de distribución acumulativa normal estándar, denominada $Φ$ , también llamada $norm(x)$ por algunos lenguajes de software, ya que solo se diferencian por el escalado y la traducción. En efecto,

la función de distribución acumulativa normal trazada en el plano complejo

{displaystyle {begin{aligned}Phi (x)&={frac {1}{sqrt {2pi }}}int _{-infty }^{x}e^{tfrac {-t^{2}}{2}},mathrm {d} t\[6pt]&={frac {1}{2}}left(1+operatorname {erf} {frac {x}{sqrt {2}}}right)\[6pt]&={frac {1}{2}}operatorname {erfc} left(-{frac {x}{sqrt {2}}}right)end{aligned}}}

o reorganizado para $erf$ y $erfc$ :

{displaystyle {begin{aligned}operatorname {erf} (x)&=2Phi left(x{sqrt {2}}right)-1\[6pt]operatorname {erfc} (x)&=2Phi left(-x{sqrt {2}}right)\&=2left(1-Phi left(x{sqrt {2}}right)right).end{aligned}}}

En consecuencia, la función de error también está estrechamente relacionada con la función Q, que es la probabilidad de cola de la distribución normal estándar. La función Q se puede expresar en términos de la función de error como

{displaystyle {begin{aligned}Q(x)&={frac {1}{2}}-{frac {1}{2}}operatorname {erf} {frac {x}{sqrt {2}}}\&={frac {1}{2}}operatorname {erfc} {frac {x}{sqrt {2}}}.end{aligned}}}

La función inversa de $Φ$ se conoce como función cuantil normal o función probit y puede expresarse en términos de la función de error inversa como

{displaystyle operatorname {probit} (p)=Phi ^{-1}(p)={sqrt {2}}operatorname {erf} ^{-1}(2p-1)=-{sqrt {2}}operatorname {erfc} ^{-1}(2p).}

La cdf normal estándar se usa más a menudo en probabilidad y estadística, y la función de error se usa más a menudo en otras ramas de las matemáticas.

La función de error es un caso especial de la función de Mittag-Leffler y también se puede expresar como una función hipergeométrica confluente (función de Kummer):

{displaystyle operatorname {erf} x={frac {2x}{sqrt {pi }}}Mleft({tfrac {1}{2}},{tfrac {3}{2}},-x^{2}right).}

Tiene una expresión simple en términos de la integral de Fresnel.

En términos de la función gamma regularizada $P$ y la función gamma incompleta,

{displaystyle operatorname {erf} x=operatorname {sgn} xcdot Pleft({tfrac {1}{2}},x^{2}right)={frac {operatorname {sgn} x}{sqrt {pi }}}gamma left({tfrac {1}{2}},x^{2}right).}

$sgn x$ es la función de signo.

Funciones de error generalizado

Gráfico de funciones de error generalizadas

E n () x)

:
curva gris:

E 1 () x) 1 - e - x / \sqrt π

curva roja:

E 2 () x) = erf(x)

curva verde:

E 3 () x)

curva azul:

E 4 () x)

curva de oro:

E 5 () x)

Algunos autores analizan las funciones más generales:

{displaystyle E_{n}(x)={frac {n!}{sqrt {pi }}}int _{0}^{x}e^{-t^{n}},mathrm {d} t={frac {n!}{sqrt {pi }}}sum _{p=0}^{infty }(-1)^{p}{frac {x^{np+1}}{(np+1)p!}}.}

Casos notables son:

$E 0 () x)$ es una línea recta a través del origen: $E 0 () x) x / e \sqrt π$
$E 2 () x)$ es la función de error, $er x$ .

Después de la división por $n!$ , todos los $E n$ para impares $n$ parecen similares (pero no idénticos) entre sí. Del mismo modo, $E n$ incluso para $n$ parecen similares (pero no idénticos) entre sí después de una simple división por $n!$ . Todas las funciones de error generalizadas para $n > 0$ tienen un aspecto similar en el lado positivo $x$ del gráfico.

Estas funciones generalizadas pueden expresarse de manera equivalente para $x > 0$ usando la función gamma y la función gamma incompleta:

0.}" xmlns="http://www.w3.org/1998/Math/MathML">En()x)=1π π .. ()n)().. ()1n)− − .. ()1n,xn)),x■0.{displaystyle E_{n}(x)={frac {1}{sqrt {cH00} {cH00} {cH00} {cH00} {cH00}} {cH00}} {cH00} {cH00} {fn}} {fn}} {cHFF} {f}} {cH00}} {cH00}}} {f} {f}}}}} {f}}}}}}}}}}} {f} {f} {f} {f}f}}}}}f}f} {f}f}f}f}}}f}f}f}f}f}f}fnf}fnf} {sqf} {fnsqf}f} {fnfnfnfnfnf}fnf}}f}f}}f} {fn }}Gamma (n)left(Gamma left({frac {1}{n}right)-Gamma left({frac {1}{n},x^{n}right)right),qquad x confianza0.}0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ff23b0f564948d88a81f7846c4869a84640c1115" style="vertical-align: -2.838ex; width:55.45ex; height:6.509ex;"/>

Por lo tanto, podemos definir la función de error en términos de la función gamma incompleta:

{displaystyle operatorname {erf} x=1-{frac {1}{sqrt {pi }}}Gamma left({tfrac {1}{2}},x^{2}right).}

Integrales iteradas de la función de error complementaria

Las integrales iteradas de la función de error complementaria están definidas por

{displaystyle {begin{aligned}operatorname {i} ^{n}!operatorname {erfc} z&=int _{z}^{infty }operatorname {i} ^{n-1}!operatorname {erfc} zeta ,mathrm {d} zeta \[6pt]operatorname {i} ^{0}!operatorname {erfc} z&=operatorname {erfc} z\operatorname {i} ^{1}!operatorname {erfc} z&=operatorname {ierfc} z={frac {1}{sqrt {pi }}}e^{-z^{2}}-zoperatorname {erfc} z\operatorname {i} ^{2}!operatorname {erfc} z&={tfrac {1}{4}}left(operatorname {erfc} z-2zoperatorname {ierfc} zright)\end{aligned}}}

La fórmula de recurrencia general es

{displaystyle 2ncdot operatorname {i} ^{n}!operatorname {erfc} z=operatorname {i} ^{n-2}!operatorname {erfc} z-2zcdot operatorname {i} ^{n-1}!operatorname {erfc} z}

Tienen la serie de potencias

{displaystyle operatorname {i} ^{n}!operatorname {erfc} z=sum _{j=0}^{infty }{frac {(-z)^{j}}{2^{n-j}j!,Gamma left(1+{frac {n-j}{2}}right)}},}

de donde se siguen las propiedades de simetría

{displaystyle operatorname {i} ^{2m}!operatorname {erfc} (-z)=-operatorname {i} ^{2m}!operatorname {erfc} z+sum _{q=0}^{m}{frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}}

{displaystyle operatorname {i} ^{2m+1}!operatorname {erfc} (-z)=operatorname {i} ^{2m+1}!operatorname {erfc} z+sum _{q=0}^{m}{frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}.}

Implementaciones

Como función real de un argumento real

En sistemas operativos compatibles con POSIX, el encabezado math.h declarar y la biblioteca matemática libm proporcionará las funciones erf y erfc (doble precisión) así como sus contrapartes de precisión y precisión ampliadas erff, erfl y erfcf, erfcl.

La Biblioteca Científica GNU proporciona erf, erfc, log(erf), y funciones de error escaladas.

Como función compleja de un argumento complejo

libcerf, numérico Biblioteca C para funciones complejas de error, proporciona las funciones complejas cerf, cerfc, cerfcx y las funciones reales erfi, erfcx con una precisión aproximada de 13 a 14 dígitos, basada en la función Faddeeva como implementada en el paquete MIT Faddeeva

Contenido relacionado

Más resultados...