Función de distribución acumulativa

a{displaystyle a}

b{displaystyle b}

fX{displaystyle F_{X}

FX{displaystyle F_{X}

X{displaystyle X}

Si X{displaystyle X} tiene L1-norm finito, es decir, la expectativa de SilencioXSilencio{displaystyle Silencioso es finito, entonces

E[X]=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO tdFX()t){displaystyle mathbb [X]=int _{-infty } {infty }tdF_{X}(t)}

x≥ ≥ 0{displaystyle xgeq 0}

Parcela CDF con dos rectángulos rojos, ilustrando x()1− − FX()x))≤ ≤ ∫ ∫ xJUEGO JUEGO tdFX()t){displaystyle x(1-F_{X}(x))leq int _{x}^{infty }tdF_{X}(t)} y xFX()− − x)≤ ≤ ∫ ∫ − − JUEGO JUEGO − − x()− − t)dFX()t){displaystyle xF_{X}(-x)leq int _{-infty }^{-x}(-t)dF_{X}(t)}.

x()1− − FX()x))≤ ≤ ∫ ∫ xJUEGO JUEGO tdFX()t)xFX()− − x)≤ ≤ ∫ ∫ − − JUEGO JUEGO − − x()− − t)dFX()t){displaystyle {begin{aligned}x(1-F_{X}(x) Pulseleqint _{x}^{infty }tdF_{X}(t)xF_{X}(-x) {leqint _{-x} {f} {f}t} {f}t}t} {f}t}t} {f}t} {f}t}t}t}t}t}t} {c]

En particular, tenemos

limx→ → − − JUEGO JUEGO xF()x)=0,limx→ → +JUEGO JUEGO x()1− − F()x))=0.{displaystyle lim _{xto -infty }xF(x)=0,quad lim _{xto +infty }x(1-F(x)=0.}

Ejemplos

Como ejemplo, supongamos X{displaystyle X} se distribuye uniformemente en el intervalo de unidad [0,1]{displaystyle [0,1]}.

Luego el CDF X{displaystyle X} es dado por

Supongamos que en lugar de eso X{displaystyle X} toma sólo los valores discretos 0 y 1, con igual probabilidad.

Luego el CDF X{displaystyle X} es dado por

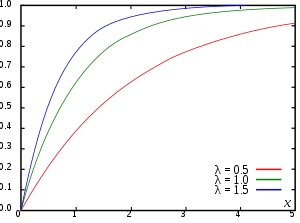
Suppose X{displaystyle X} es exponencial distribuido. Luego el CDF X{displaystyle X} es dado por

Aquí λ > 0 es el parámetro de la distribución, a menudo llamado parámetro de tasa.

Suppose X{displaystyle X} es normal distribuido. Luego el CDF X{displaystyle X} es dado por

F()x;μ μ ,σ σ )=1σ σ 2π π ∫ ∫ − − JUEGO JUEGO xexp⁡ ⁡ ()− − ()t− − μ μ )22σ σ 2)dt.{displaystyle F(x;musigma)={frac {1}{sigma {sqrt {2pi}}}int _{-infty }{x}exp left(-{frac {(t-mu)}{2sigma ^{2}}right),dt.}

Aquí el parámetro μ μ {displaystyle mu } es la media o expectativa de la distribución; y σ σ {displaystyle sigma } es su desviación estándar.

Una tabla de la CDF de la distribución normal estándar se usa a menudo en aplicaciones estadísticas, donde se denomina tabla normal estándar, tabla normal de unidades o tabla Z.

Suppose X{displaystyle X} es binomial distribuido. Luego el CDF X{displaystyle X} es dado por

F()k;n,p)=Pr()X≤ ≤ k)=.. i=0⌊ ⌊ k⌋ ⌋ ()ni)pi()1− − p)n− − i{displaystyle F(k;n,p)=Pr(Xleq k)=sum _{i=0}^{lfloor krfloor }{nchoose i}p^{i}(1-p)^{n-i}}} {cH00}

Aquí. p{displaystyle p} es la probabilidad del éxito y la función denota la distribución discreta de probabilidad del número de éxitos en una secuencia de n{displaystyle n} experimentos independientes, y ⌊ ⌊ k⌋ ⌋ {displaystyle lfloor krfloor } es el "flor" bajo k{displaystyle k}, es decir, el mayor entero menos o igual a k{displaystyle k}.

Funciones derivadas

Función de distribución acumulativa complementaria (distribución de cola)

A veces, es útil estudiar la pregunta opuesta y preguntar con qué frecuencia la variable aleatoria está por encima de un nivel particular. Esto se denomina función de distribución acumulativa complementaria (ccdf) o simplemente distribución de cola o excedencia, y se define como

x)=1-F_{X}(x).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">F̄ ̄ X()x)=P⁡ ⁡ ()X■x)=1− − FX()x).{displaystyle {bar}_{X}(x)=operatorname {P} (X títulox)=1-F_{X}(x). }

x)=1-F_{X}(x).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d15665a3d46120b6740ccce9d8e32ec9458c37a8" style="vertical-align: -0.838ex; width:33.489ex; height:3.009ex;"/>

Esto tiene aplicaciones en pruebas de hipótesis estadísticas, por ejemplo, porque el valor p unilateral es la probabilidad de observar una estadística de prueba al menos tan extremo como el observado. Así, siempre que la estadística de prueba, T, tiene una distribución continua, el valor p unilateral es simplemente dado por el ccdf: para un valor observado t{displaystyle t} de la estadística de prueba

t)=1-F_{T}(t).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">p=P⁡ ⁡ ()T≥ ≥ t)=P⁡ ⁡ ()T■t)=1− − FT()t).{displaystyle p= {P}(Tgeq t)=operatorname {P} (T Conft)=1-F_{T}(t). }

t)=1-F_{T}(t).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/779dc6f3668f7d0ffab59059e3edab09fef014b5" style="vertical-align: -0.838ex; margin-left: -0.089ex; width:38.67ex; height:2.843ex;"/>

En análisis de supervivencia, F̄ ̄ X()x){displaystyle {bar}_{X}(x)} se llama función de supervivencia y denotado S()x){displaystyle S(x)}, mientras que el término función de confiabilidad es común en ingeniería.

Propiedades

• Para una variable aleatoria continua no negativa que tiene una expectativa, la desigualdad de Markov afirma que
  F̄ ̄ X()x)≤ ≤ E⁡ ⁡ ()X)x.{displaystyle {bar {f}_{X}(x)leq {frac {fone {f}{x}}}}}}

  
• As x→ → JUEGO JUEGO ,F̄ ̄ X()x)→ → 0{displaystyle xtoinfty{bar}_{X}(x)to 0}, y de hecho F̄ ̄ X()x)=o()1/x){displaystyle {bar {f}_{X}(x)=o(1/x)} siempre que E⁡ ⁡ ()X){displaystyle operatorname {E} (X)} es finito.
  Prueba:
  Sumas X{displaystyle X} tiene una función de densidad fX{displaystyle F_{X}, para cualquier 0}" xmlns="http://www.w3.org/1998/Math/MathML">c■0{displaystyle c]0} 0 " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba126f626d61752f62eaacaf11761a54de4dc84" style="vertical-align: -0.338ex; width:5.268ex; height:2.176ex;"/>
  E⁡ ⁡ ()X)=∫ ∫ 0JUEGO JUEGO xfX()x)dx≥ ≥ ∫ ∫ 0cxfX()x)dx+c∫ ∫ cJUEGO JUEGO fX()x)dx{displaystyle operatorname [E]=int _{0}{infty }xf_{X}(x),dxgeq int ¿Por qué?

  
  Entonces, reconociendo
  F̄ ̄ X()c)=∫ ∫ cJUEGO JUEGO fX()x)dx{displaystyle {bar {f}_{X}(c)=int _{c}{infty }f_{X}(x),dx}

  
  y términos de reorganización,
  0≤ ≤ cF̄ ̄ X()c)≤ ≤ E⁡ ⁡ ()X)− − ∫ ∫ 0cxfX()x)dx→ → 0comoc→ → JUEGO JUEGO {displaystyle 0leq c{bar} {F}_{X}(c)leq operatorname {E} (X)-int _{0}^{c}xf_{X}(x),dxto 0{text{ as }cto infty }

  
  como se afirma.
• Para una variable aleatoria que tenga una expectativa,
  E⁡ ⁡ ()X)=∫ ∫ 0JUEGO JUEGO F̄ ̄ X()x)dx− − ∫ ∫ − − JUEGO JUEGO 0FX()x)dx{displaystyle operatorname [E]=int _{0}{infty }{bar {F}_{X}(x),dx-int _{-infty } {0}F_{X}(x),dx}

  
  y para una variable aleatoria no negativa el segundo término es 0.
  Si la variable aleatoria sólo puede tomar valores enteros no negativos, esto es equivalente a
  E⁡ ⁡ ()X)=.. n=0JUEGO JUEGO F̄ ̄ X()n).{displaystyle operatorname (X)=sum _{n=0}{infty}{bar {F}_{X}(n)}

  

Distribución acumulada plegada

Ejemplo de la distribución acumulativa plegada para una función de distribución normal con un valor esperado de 0 y una desviación estándar de 1.

Mientras la trama de una distribución acumulativa F{displaystyle F} a menudo tiene una forma similar a S, una ilustración alternativa es la distribución acumulativa plegada o parcela de montaña, que dobla la mitad superior del gráfico sobre, es

0.5}}}" xmlns="http://www.w3.org/1998/Math/MathML">Fplegable()x)=F()x)1{}F()x)≤ ≤ 0.5}+()1− − F()x))1{}F()x)■0.5}{displaystyle F_{text{fold}(x)=F(x)1_{F(x)leq 0.5}+(1-F(x))1_{F(x)0.5}}}}0.5}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/64fb171fc50495773d22a592a91603af18b6170b" style="vertical-align: -1.171ex; width:48.811ex; height:3.176ex;"/>

Donde 1{}A}{displaystyle 1_{{A}}} denota la función indicadora y la segunda suma es la función sobreviviente, utilizando así dos escalas, una para la pendiente y otra para la pendiente. Esta forma de ilustración hace hincapié en la mediana, la dispersión (específicamente, la mediana desviación absoluta) y la asiduidad de la distribución o de los resultados empíricos.

Función de distribución inversa (función cuantil)

Si el CDF F es estrictamente creciente y continuo entonces F− − 1()p),p▪ ▪ [0,1],{displaystyle F^{-1}(p),pin [0,1],} es el número real único x{displaystyle x} tales que F()x)=p{displaystyle F(x)=p}. Esto define el función de distribución inversa o función cuántil.

Algunas distribuciones no tienen un inverso único (por ejemplo, si fX()x)=0{displaystyle f_{X}(x)=0} para todos <math alttext="{displaystyle a<xa.x.b{displaystyle a seccionóx<img alt="a<x, causando FX{displaystyle F_{X} ser constante). En este caso, se puede utilizar el función generalizada de distribución inversa, que se define como

F− − 1()p)=inf{}x▪ ▪ R:F()x)≥ ≥ p},О О p▪ ▪ [0,1].{displaystyle F^{-1}(p)=inf{xin mathbb {R}:F(x)geq p},quad forall pin [0,1]. }

• Ejemplo 1: La mediana es F− − 1()0.5){displaystyle F^{-1}(0.5)}.
• Ejemplo 2: Poner τ τ =F− − 1()0.95){displaystyle tau =F^{-1}(0.95)}. Entonces llamamos τ τ {displaystyle tau } el percentil 95.

Algunas propiedades útiles de la cdf inversa (que también se conservan en la definición de la función de distribución inversa generalizada) son:

1. F− − 1{displaystyle F^{-1} no está adelgazando
2. F− − 1()F()x))≤ ≤ x{displaystyle F^{-1}(F(x)leq x}
3. F()F− − 1()p))≥ ≥ p{displaystyle F(F^{-1}(p)geq p}
4. F− − 1()p)≤ ≤ x{displaystyle F^{-1}(p)leq x} si p≤ ≤ F()x){displaystyle pleq F(x)}
5. Si Y{displaystyle Sí. tiene U[0,1]{displaystyle U[0,1]} distribución F− − 1()Y){displaystyle F^{-1}(Y)} se distribuye como F{displaystyle F}. Esto se utiliza en la generación de números aleatorios utilizando el muestreo de transformación inversa-método.
6. Si {}Xα α }{displaystyle {X_{alpha } es una colección independiente F{displaystyle F}- variables aleatorias distribuidas definidas en el mismo espacio de muestra, entonces existen variables aleatorias Yα α {displaystyle Y... tales que Yα α {displaystyle Y... se distribuye como U[0,1]{displaystyle U[0,1]} y F− − 1()Yα α )=Xα α {displaystyle F^{-1}(Y_{alpha }=X_{alpha } con probabilidad 1 para todos α α {displaystyle alpha }.

La inversa de la cdf se puede utilizar para traducir los resultados obtenidos para la distribución uniforme a otras distribuciones.

Función de distribución empírica

La función de distribución empírica es una estimación de la función de distribución acumulativa que generó los puntos de la muestra. Converge con probabilidad 1 a esa distribución subyacente. Existen varios resultados para cuantificar la tasa de convergencia de la función de distribución empírica a la función de distribución acumulativa subyacente.

Caso multivariante

Definición de dos variables aleatorias

Al tratar simultáneamente con más de una variable al azar función conjunta de distribución acumulativa también se puede definir. Por ejemplo, para un par de variables aleatorias X,Y{displaystyle X,Y}, el CDF conjunto FXY{displaystyle F_{XY} es dado por

FX,Y()x,Sí.)=P⁡ ⁡ ()X≤ ≤ x,Y≤ ≤ Sí.){displaystyle F_{X,Y}(x,y)=operatorname (Xleq x,Yleq y)}

()Eq.3)

donde el lado derecho representa la probabilidad de que la variable aleatoria X{displaystyle X} tiene un valor inferior o igual a x{displaystyle x} y que Y{displaystyle Sí. tiene un valor inferior o igual a Sí.{displaystyle y}.

Ejemplo de función de distribución acumulativa conjunta:

Para dos variables continuas X e Y:

Para dos variables aleatorias discretas, es beneficioso generar una tabla de probabilidades y abordar la probabilidad acumulada para cada rango potencial de X e Y, y aquí está la ejemplo:

Dada la función de masa de probabilidad conjunta en forma tabular, determine la función de distribución acumulativa conjunta.

Solución: usando la tabla de probabilidades dada para cada rango potencial de X e Y, la función de distribución acumulada conjunta se puede construir en forma tabular:

Definición de más de dos variables aleatorias

Para N{displaystyle N} variables aleatorias X1,...... ,XN{displaystyle X_{1},ldotsX_{N}, el CDF conjunto FX1,...... ,XN{displaystyle F_{X_{1},ldotsX_{N}} es dado por

FX1,...... ,XN()x1,...... ,xN)=P⁡ ⁡ ()X1≤ ≤ x1,...... ,XN≤ ≤ xN){displaystyle F_{X_{1},ldotsX_{N}(x_{1},ldotsx_{N}=operatorname {P} (X_{1}leq x_{1},ldotsX_{N}leq x_{N}}

()Eq.4)

Interpretación de N{displaystyle N} variables aleatorias como vector aleatorio X=()X1,...... ,XN)T{displaystyle mathbf {X} =(X_{1},ldotsX_{N} {T}} produce una notación más corta:

FX()x)=P⁡ ⁡ ()X1≤ ≤ x1,...... ,XN≤ ≤ xN){displaystyle F_{Mathbf [X] }(mathbf {x}=operatorname {P} (X_{1}leq x_{1},ldotsX_{N}leq x_{N}}

Propiedades

Cada CDF multivariante es:

1. Monotonically non-decreasing for each of its variables,
2. Derecho continuo en cada una de sus variables,
3. 0≤ ≤ FX1...... Xn()x1,...... ,xn)≤ ≤ 1,{displaystyle 0leq F_{X_{1}ldots X_{n}(x_{1},ldotsx_{n})leq 1,}
4. limx1,...... ,xn→ → +JUEGO JUEGO FX1...... Xn()x1,...... ,xn)=1ylimxi→ → − − JUEGO JUEGO FX1...... Xn()x1,...... ,xn)=0,para todosi.{displaystyle lim _{x_{1},ldotsx_{n}rightarrow ####infty }F_{X_{1}ldots X_{n}(x_{1},ldotsx_{n})=1{text{ and }lim ################################################################################################################################################################################################################################################################ - ¿Qué?

   

Cualquier función que satisfaga las cuatro propiedades anteriores no es un CDF multivariable, a diferencia del caso de dimensión única. Por ejemplo, vamos F()x,Sí.)=0{displaystyle F(x,y)=0} para <math alttext="{displaystyle xx.0{displaystyle x realizadas0}<img alt="x o <math alttext="{displaystyle x+yx+Sí..1{displaystyle x+y won1}<img alt="{displaystyle x+y o <math alttext="{displaystyle ySí..0{displaystyle y won0}<img alt="{displaystyle y y dejar F()x,Sí.)=1{displaystyle F(x,y)=1} De lo contrario. Es fácil ver que las condiciones anteriores se cumplen, y sin embargo F{displaystyle F} no es un CDF ya que si lo fuera, entonces <math alttext="{textstyle operatorname {P} left({frac {1}{3}}<Xleq 1,{frac {1}{3}}P⁡ ⁡ ()13.X≤ ≤ 1,13.Y≤ ≤ 1)=− − 1{textstyle operatorname {P} left({frac {1}{3}SeleccionóXleq 1,{frac {1}{3} {Yleq 1right)=-1}<img alt="{textstyle operatorname {P} left({frac {1}{3}}<Xleq 1,{frac {1}{3}} como se explica a continuación.

La probabilidad de que un punto pertenezca a un hiperrectángulo es análoga al caso unidimensional:

Caso complejo

Variable aleatoria compleja

La generalización de la función de distribución acumulativa de variables aleatorias reales a complejas no es obvia porque las expresiones de la forma P()Z≤ ≤ 1+2i){displaystyle P(Zleq 1+2i)} no tiene sentido. Sin embargo expresiones de la forma P()R R ()Z)≤ ≤ 1,I I ()Z)≤ ≤ 3){displaystyle P(Re {(Z)}leq 1,Im {(Z)}leq 3)} tiene sentido. Por lo tanto, definimos la distribución acumulativa de variables complejas aleatorias a través de la distribución conjunta de sus partes reales e imaginarias:

FZ()z)=FR R ()Z),I I ()Z)()R R ()z),I I ()z))=P()R R ()Z)≤ ≤ R R ()z),I I ()Z)≤ ≤ I I ()z)).{displaystyle F_{Z}(z)=F_{Re {(Z)},Im {(Z)}(Re {(z)},Im {(z)})=P(Re {(Z)}leq Re {(z)},Im {(Z)}leqIm {(z)}). }

Vector aleatorio complejo

La generalización de los rendimientos de la ecuación 4

FZ()z)=FR R ()Z1),I I ()Z1),...... ,R R ()Zn),I I ()Zn)()R R ()z1),I I ()z1),...... ,R R ()zn),I I ()zn))=P⁡ ⁡ ()R R ()Z1)≤ ≤ R R ()z1),I I ()Z1)≤ ≤ I I ()z1),...... ,R R ()Zn)≤ ≤ R R ()zn),I I ()Zn)≤ ≤ I I ()zn))################################################################################################################################################################################################################################################################ Re {Z_{n}}leq {fn} {fn}mfn}leq Im {(z_{n})}}}

Z=()Z1,...... ,ZN)T{displaystyle mathbf {Z} =(Z_{1},ldotsZ_{N} {T}

Uso en análisis estadístico

El concepto de función de distribución acumulativa hace una aparición explícita en el análisis estadístico de dos formas (similares). El análisis de frecuencia acumulativa es el análisis de la frecuencia de ocurrencia de valores de un fenómeno menores que un valor de referencia. La función de distribución empírica es una estimación directa formal de la función de distribución acumulativa para la cual se pueden derivar propiedades estadísticas simples y que puede formar la base de varias pruebas de hipótesis estadísticas. Tales pruebas pueden evaluar si hay evidencia contra una muestra de datos que surgió de una distribución dada, o evidencia contra dos muestras de datos que surgieron de la misma distribución de población (desconocida).

Pruebas de Kolmogorov-Smirnov y Kuiper

La prueba de Kolmogorov-Smirnov se basa en funciones de distribución acumulativa y se puede utilizar para comprobar si dos distribuciones empíricas son diferentes o si una distribución empírica es diferente de una distribución ideal. La prueba de Kuiper, estrechamente relacionada, es útil si el dominio de la distribución es cíclico como en el día de la semana. Por ejemplo, la prueba de Kuiper podría usarse para ver si la cantidad de tornados varía durante el año o si las ventas de un producto varían según el día de la semana o el día del mes.